Анализ метрических характеристик двулетних побеговых систем Acer negundo L. в молодом генеративном состоянии

Введение. Основной метод выявления в теле растения повторяющихся частей разного масштаба, разработанный И.Г. Серебряковым, опирался на представления о ритмичности процессов формообразования (Серебряков, 1952; Гатцук, 2008). Этот метод позволяет рассматривать строение любого дерева как разворачивающуюся программу развития. Жизненная форма «дерево» в этом смысле уникальна, так как позволяет проследить

Вестник ТвГУ. Серия "Биология и экология". 2016. № 4. морфологическую реализацию всей предшествующей программы. Подробное исследование кроны дает возможность охарактеризовать разные элементы кроны как пространственно-временные модули ее строения.

Последние 25 лет предпринимались многочисленные попытки выделения структурных элементов кроны (Мазуренко, Хохряков, 1991; Barthelemy, Caraglio, 2007; Гацук, 2008; Гетманец, 2008 и др.). Лишь для начальных единиц этих класификаций - побега и междоузлия - существуют объективные критерии их оценки, так как эти элементы столетиями составляли предмет изучения ботаников в разных исследованиях. Свойства побеговых систем представлены, как правило, только на описательном уровне. При этом, как известно, побеговые системы разного ранга обладают свойством эмерджентности и их свойства, безусловно, заслуживают самостоятельного изучения именно как характеристики пространственно-временных единиц строения кроны.

• A. negundo - заносный вид, широко распространенный в европейской части Российской Федерации, разносторонне исследуется как с морфологической, так и с популяционной точек зрения (Михайлевская, 2001; Виноградова, 2006; Виноградова и др., 2009; Костина и др., 2013; Веселкин, Прокина, 2016). Тем не менее, строение кроны этого древесного растения в литературе представлено в основном на описательном уровне.

Цель работы - исследование типов двулетних побеговых систем и их свойств в самом общем виде на примере A. negundo.

Методика. Исследованы 3 группы растений A. negundo, произрастающих в лесостепной зоне в окрестностях заповедника «Белогорье», Белгородская область (база данных ANTREES¹).

Для исследования из зарослей, возобновляющихся семенным путем, выбирались хорошо развитые, полностью освещенные, женские растения в возрастном состоянии G1. Две популяции растений произрастали в разных местах при хорошем водоснабжении, в понижении увалисто-балочного рельефа, а одна популяция - в сухом местообитании, на высоком берегу р. Ворскла, где уровень увлажнения определяется количеством выпадающих осадков (грунтовая вода на глубине 20 м). Материал собран в конце июля 2012 г. Общее количество исследованных деревьев в первом местообитании

• - 10, во втором — 20, в третьем - 4. Абсолютный возраст изученных особей данного возрастного состояния в первом местообитании составлял 8-13 лет, во втором -8-15 лет, в третьем -9-18 лет.

У исследованных растений были измерены все побеги дерева по следующим признакам: длина побега, для части побегов - длина междоузлий, для всех побегов - количество листьев, а где возможно -и количество листовидных органов (катафиллов и чешуй), год образования побега, угол отхождения побега от материнского, наличие генеративных побегов (отмечалось характеристикой «плод»). Для каждой особи составлена подробная схема с указанием размерных характеристик и проведено фотографирование целого дерева и отдельных ветвей.

На основе разработанного ранее представления о строении двулетних побеговых систем (ДПС) проведена типизация побеговых систем побеговых растений (Антонова, Гниловская, 2013).

Для моделирования процедуры типизации ДПС A. negundo применялись однофакторный дисперсионный анализ (ANOVA), пошаговый дискриминантный анализ и кластерный анализ для построения визуального решающего правила (Рао, 1963; Hastie et al., 2014). Анализ гистограммы длин побегов был использован для их разделения на группы (Дженкинс, Ватте, 1971). В зависимости от природы некоторых метрических признаков их значения были логарифмированы или ранжированы. В качестве разведывательного анализа при выяснении структуры различных метрических характеристик ДПС применялся метод главных компонент, различные описательные статистики. Для проверки распределений значений признаков в интервалах применялись критерии Колмогорова -Смирнова и Лиллиефорса. В вычислениях авторы опирались на пакеты компьютерных программ R (Insightful, Inc.) и STATISTICA 10 (StatSoft, Inc.).

Результаты и обсуждение. Геометрический контур двулетней побеговой системы A. negundo представляет собой трехмерную фигуру, построенную на основании соединения наиболее удаленных точек боковых побегов и концов материнского побега.

На самом деле, контур образован целым рядом признаков материнского и его боковых побегов. У материнского побега существенны длина, распределение междоузлий по длине, а, следовательно, количество листовидных органов. Используемые признаки боковых побегов - их вегетативность или генеративность, размещение боковой почки на материнском побеге и особенности ее ветвления, длина, угол ответвления от материнской оси.

Ранее при описании ДПС в разных возрастных состояниях A. negundo была отмечена связь длин боковых побегов с определенными углами ответвления, что определяет понятие геометрического контура и типизацию ДПС (Антонова, Гниловская, 2013). A. negundo отличается от других древесных растений большей значимостью и устойчивостью признаков длин побегов по отношению к признакам количества междоузлий на них (Антонова и др., 2012; Савиных, 2014). Остановимся на показателях длин боковых побегов как на основных характеристиках геометрического контура.

Для определения состава одного дерева по типам ДПС было выбрано дерево из хорошо увлажненного местообитания. Высота дерева составляет 5395 мм при максимальной ширине кроны 3045 мм. Абсолютный возраст 8 лет. Дерево имеет 4 порядка ветвления. Длина побегов этого растения варьирует от 15 мм до 1520 мм. Количество скелетных побегов, то есть побегов, входящих в главную ось и в крупные оси второго порядка, составляет 1,9%. Отношение прироста скелетных побегов к остальным за последний год составило 1%. Четвертый порядок ветвления имеют 64 побега, третий - 223, второй -129, первый - 8. Общее количество побегов на дереве 422. Хорошо заметно, что появление плодов, то есть переход к генеративному развитию, приводит к торможению роста количества порядков ветвления в кроне дерева.

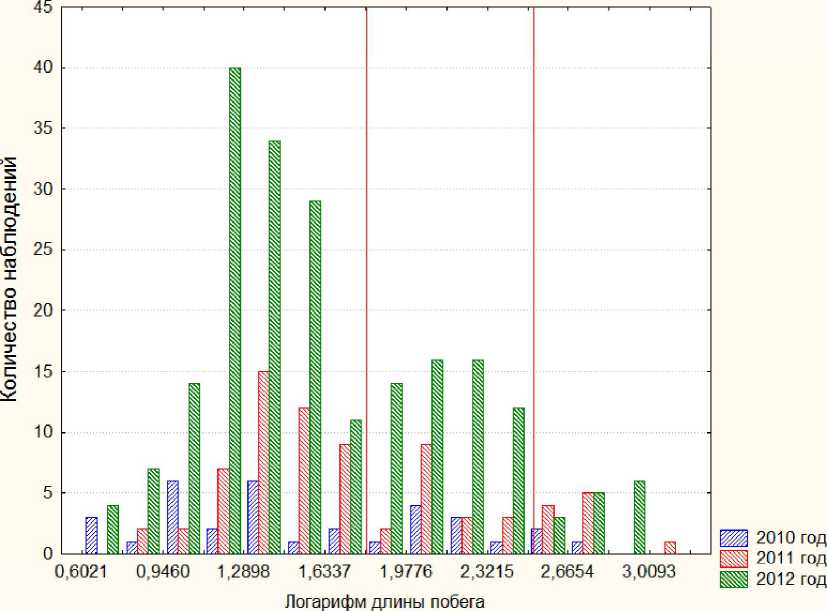
Рис. 1. Длины всех побегов за последние три года в логарифмическом масштабе для дерева 27

Гистограмма на рисунке 1 обнаруживает деление всех побегов кроны на три группы с модальными значениями распределений, устойчивыми относительно процедуры «стягивания окна» (изменения интервала гистограммы). В соответствии с этим побеги были разбиты на три группы (см. рис. 1): короткие - до 80 мм, средние - от 81 мм до 400 мм, длинные - более 400 мм.

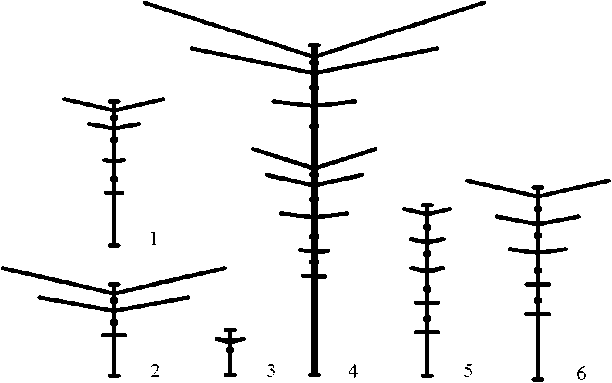
Рис. 2 . Схематическое визуальное деление ДПС Acer negundo на типы: 1 - основная, 2 - вертолет, 3 - заполняющая, 4 - сверхростовая, 5 - расставка, б - ростовая

Значительный прирост общего количества побегов в 2012 г. отражает успешное развитие особи, а доминирование в нем коротких побегов при существенном увеличении количества побегов малой и средней длины связано с переходом к генеративной фазе развития.

Таблица 1

Распределение ДПС дерева №27 по годам

Год	Типы ДПС						Всего
	Зап.	Верт.	Осн.	Расст.	Рост.	Сверх.
2011	48		3	14	6	1	72
2010	22	3	1	6	1		33
2009	3			2		1	6
Всего	73	3	4	22	7	2	111

Типизация всех побеговых систем этого дерева выявила кроме ювенильной и имматурной двулетних побеговых систем в основании ствола, присутствие еще 6 типов ДПС (см. Антонова, Гниловская, 2013). '

Перечислим ДПС по возрастанию их количества в кроне в возрастном состоянии G1: «сверхростовые», «переходные» (называемые теперь за крупные боковые побеги при малой длине материнского - «вертолеты»), «основные», «ростовые», «расставки», «заполняющие».

В табл. 1 представлен полный состав ДПС. Заметим, что, на побегах 2012 г. ДПС еще не сформированы.

Общее количество ДПС на дереве - 111 (не считая двух нижних, которые классифицируются как «ювенильная» и «имматурная»). В текущем возрастном состоянии подавляющее большинство ДПС составляют «заполняющие», то есть системы длиной не более 100 мм. Крупные кронообразующие побеговые системы - «сверхростовые», длина материнского побега здесь более 1м- представлены в единичных экземплярах.

Различные геометрические контуры ДПС образованы разным количеством боковых побегов из трех хорошо различающихся по длине групп, приведенных выше.

На рис. 3 приведена совместная диаграмма распределения длинных, средних и коротких побегов и плодов по всем шести типам ДПС одного дерева.

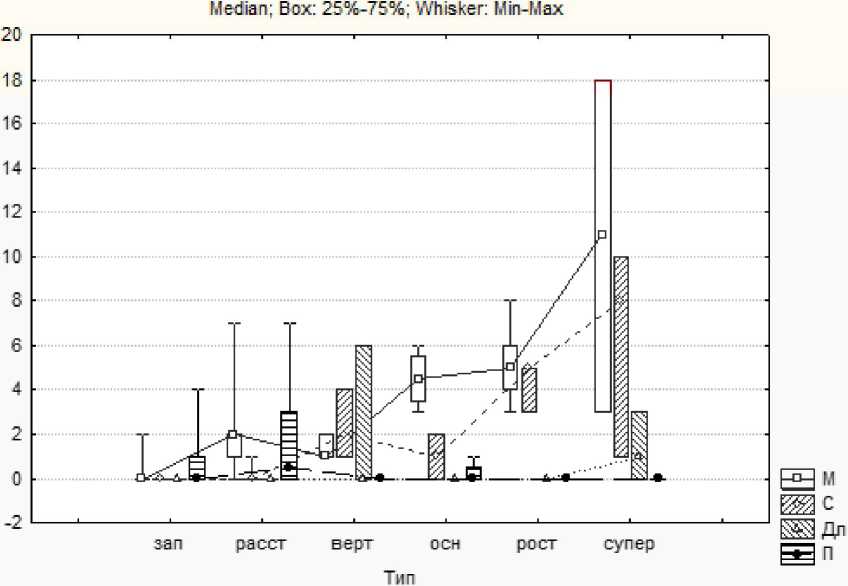
Рис. 3 . Диаграмма Тьюки «ящики с усами» распределения длинных, средних и коротких боковых побегов и плодов по 6 типам ДПС для дерева 27; М - количество коротких побегов, С - средних, Дл - длинных, П -количество плодов

ДПС заполняющего типа ветвятся очень редко и несут плоды. Наибольшее количество плодов несут «расставки». «Сверхростовые» ПС образуют наибольшее количество боковых побегов.

Для объективизации деления всех ДПС дерева на выделенные 6 типов по составу боковых побегов и плодов был применен пошаговый дискриминантный анализ. В качестве предикторов были использованы признаки: логарифм длины материнского побега (проведена проверка на нормальность распределения), ранжированные признаки количества длинных, средних и коротких боковых побегов, и плодов. В качестве групповой переменной - индикатор типов ДПС, выделенных на этом дереве визуально. F-критерий Фишера подтвердил статистическую значимость деления на типы на уровне Р < 0,00001. Подробные результаты приведены ниже.

Таблица 2

Матрица корректности классификации ДПС отдельного дерева

Тип ДПС	Корректная типизация, %	Заполн.	Расст.	Верт.	Осн.	Рост.	Сверх.
Заполн.	99	72	1	0	0	0	0
Расст.	91	0	20	0	2	0	0
Верт.	67	0	1	2	0	0	0
Осн.	50	0	2	0	2	0	0
Рост.	100	0	0	0	0	7	0
Сверх.	100	0	0	0	0	0	2
Общий	95	72	24	2	4	7	2

Таблица 3

Таблица факторных нагрузок дискриминантных функций

	Коэффициенты					Факторные веса
	ДФ1	ДФ2	ДФЗ	ДФ4	ДФ5	ДФ!	ДФ2	ДФЗ	ДФ4	ДФ5
С	-2,80	1,16	-0,45	-0,50	-0,41	-0,85	0,11	-0,23	0,45	-0,04
LogL	-0,04	-0,26	0,77	0,40	0,16	-0,40	-0,44	0,64	0,45	0,20
М	-0,45	-3,28	-1,95	-0,99	0,37	-0,30	-0,90	-0,28	-0,01	-0,17
Дл	1,18	-0,19	-0,73	1,88	0,00	-0,08	0,00	-0,45	0,89	-0,06
п	0,02	0,06	0,23	0,07	-0,74	0,04	-0,20	0,14	0,01	-0,97
Constant	2,27	5,34	2,48	1,25	-0,08
Кумулятивная доля объясненной дисперсии, % :						87,7	95,6	98,2	99,8	100,0

Примечание. М - количество коротких побегов на ДПС, С - средних, Дл - длинных, П -количество плодов, Log L - логарифм длины материнского побега ДПС.

Матрица классификации (табл. 2) определяет неплохую общую надежность (корректность) типизации - 95% (6 инверсий на 111 ДПС).

Наиболее правильную типизацию имеют «заполняющие», «ростовые» и «сверхростовые».

Основные характеристики построенных дискриминантных функций (ДФ) приведены в табл. 3. Все ДФ не коррелированы между собой и могут быть интерпретированы как независимые факторы, определяющие тип ДПС. Кроме того, они упорядочены по дисперсии (то есть, по информативности), что позволяет считать самыми существенными дискриминаторами признаки «С», «Log L» и «М». Количество длинных боковых побегов «Дл» играет роль только при выделении побеговых систем, называемых «сверхростовыми», «ростовыми» и «вертолетами», что в сумме составляет около 10% всей выборки. Это и определяет отсутствие вклада признака «Дл» в две первые дискриминантные функции. Вклад признака наличия плодов в дискриминацию также не значителен, так как они в основном характеризуют «расставки».

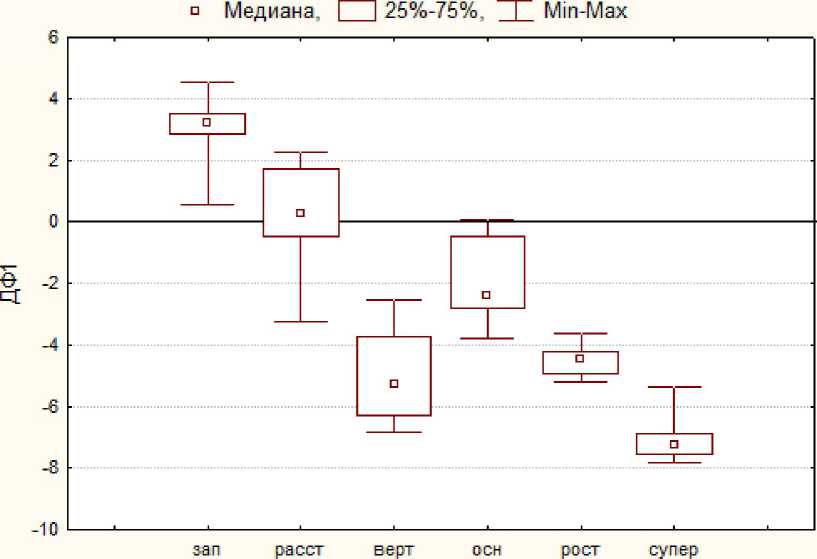
Тип ДПС

Рис. 4 . Значения первой дискриминантной функции по составу из трех типов боковых побегов и количеству плодов для шести типов ДПС дерева 27

Рис. 4 иллюстрирует выделение наиболее многочисленного типа ДПС - «заполняющих» - от всех остальных типов, кроме «расставок», по первой дискриминантной функции.

Это подтверждает предположение о жёсткости схемы размещения боковых побегов на материнском по длине, что и определяет геометрический контур ДПС. Кроме того, подтверждается адекватность нашей модели дискриминантного анализа реальной типизации. Наши предикторы улавливают то, что эксперт выделил визуально, и то, что было первоначально использовано при типизации ДПС (признаки линейные, угловые, временные и функциональные).

Полученные дискриминантные функции характеризуют вероятности попадания конкретного ДПС в свой тип на отдельном дереве по апостериорным вероятностям. Тем не менее, априорные вероятности в построенной классификации не одинаковы для разных ДПС на одном дереве из-за большой разницы в представительстве различных типов ДПС на нем (см. табл. 1).

Для проверки возможности типизации ДПС Л. negundo одного и того же возрастного состояния, независимо от конкретного дерева и местообитания выборка была дополнена по количеству ДПС в недостающих типах материалами других деревьев из разных популяций и местообитаний. Это означает изменение точки зрения - с анализа кроны одного дерева на анализ свойств именно ДПС. В новую выборку вошли: 12 «сверхростовых», 14 «ростовых», 19 «основных», 10 «вертолетов», 33 «расставки» и 73 «заполняющих». Общий объем выборки составила 161 ДПС (см. рис. 5). Растения сухого местообитания вместо «ростовых» и «вертолетов» образовывали «основные» ДПС. В их составе присутствует большее количество «заполняющих».

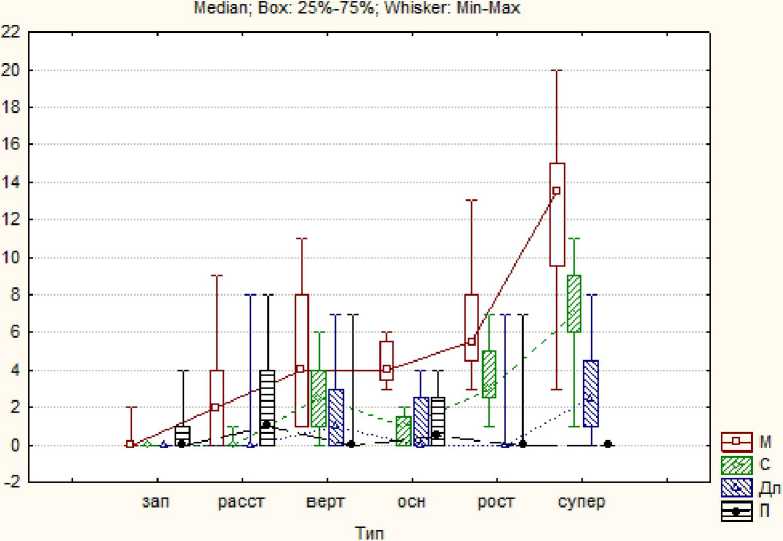
Рис. 5 . Распределение боковых побегов различной длины и плодов на материнском по типам ДПС. Обозначения те же, что и на рис. 3

Сравнение рисунков 3 и 5 свидетельствует, что внесенные в выборку дополнения, по существу, не изменили характеристики состава ДПС различных типов.

Теперь применим дискриминантный анализ по новой, увеличенной выборке, которая характеризует метрические характеристики ДПС на деревьях, собранных в местообитаниях 2 и 3 в возрастном состоянии G1. Основные результаты анализа приведены в таблицах 4 и 5.

Таблица 4

Матрица корректности классификации ДПС по расширенной выборке

Тип ДПС	Корректная типизация, %	Заполн.	Расст.	Верт.	Осн.	Рост.	Сверх.
Заполн.	99	72	1	0	0	0	0
Расст.	88	2	29	0	0	2	0
Верт.	30	0	1	3	1	2	3
Осн.	63	0	3	2	12	2	0
Рост.	93	0	0	1	0	13	0
Сверх.	75	0	0	1	0	2	9
Общий	86	74	34	7	13	21	12

Корректность типизации уменьшилась, от 94% для одного дерева до 86% для растений двух популяций, но осталась достаточно высокой.

Таблица 5

Таблица факторных нагрузок дискриминантных функций для типов ДПС по расширенной выборке

	Коэффициенты					Факторные веса
	ДФ1	ДФ2	ДФЗ	ДФ4	ДФ5	ДФ1	ДФ2	ДФЗ	ДФ4	ДФ5
С	-0,05	0,06	0,01	-0,01	-0,02	-0,76	0,58	0,17	-0,13	-0,19
LogL	-2,27	-2,93	0,98	2,73	-0,81	-0,68	-0,67	0,18	0,02	-0,24
М	-0,01	-0,01	0,00	-0,04	0,03	-0,46	-0,31	0,10	-0,58	0,59
Дл	-0,01	0,00	-0,05	0,00	0,00	-0,21	-0,13	-0,89	-0,11	-0,37
п	0,01	0,00	0,01	-0,03	-0,02	0,06	-0,31	-0,04	-0,51	-0,80
Constant	8,93	1,84	0,32	0,52	2,46
Кумулятивная доля объясненной дисперсии, % :						87,1	97,1	99,6	100,0	100,0

Анализ табл. 5 показывает, что факторные нагрузки признака «Дл» ожидаемо выросли в первых трех ДФ. Это повлияло на общую структуру нагрузок во всех ДФ, однако, структура факторов двух первых, наиболее важных ДФ принципиально не изменилась.

Полученный результат говорит о слабой зависимости предложенной типизации от свойств конкретного дерева и его местообитания в пределах одной территории. Последнее может служить так же косвенным подтверждением правильности деления ДПС на 6 типов.

Надо заметить, что использованные выше характеристики ДПС требуют массового измерения длин побегов на одном или нескольких деревьях. Задачи практики требуют сокращения количества измеряемых показателей и заставляют искать те из них, которые теснее связаны с процессом формирования ДПС.

Для этого была составлена выборка из ДПС других деревьев Л. negundo, произраставших в контрастных местообитаниях 1-3: во влажных условиях понижений увалисто-балочного рельефа и в наиболее сухих местообитаниях высокого правого берега лесостепной реки. Эта выборка была объединена с уже составленной. Объём совокупной выборки составил 218 ПС.

В качестве характеристик ДПС были взяты: логарифм длины материнского побега, количество листьев на нём, а также логарифм максимальной длины бокового побега и количество листьев на нём. Классический дискриминантный анализ по указанным признакам даёт большее количество инверсий (случаев некорректной классификации). Оказалось, что ни количество листьев на материнском побеге, ни количество листьев на боковом побеге при пошаговой процедуре дискриминантного анализа не включаются в итоговую модель. Это свидетельствует о низкой информативности (по Фишеру) показателей количества листьев, по крайней мере, для линейного метода типизации (Рао, 1968; Hastie et al., 2014).

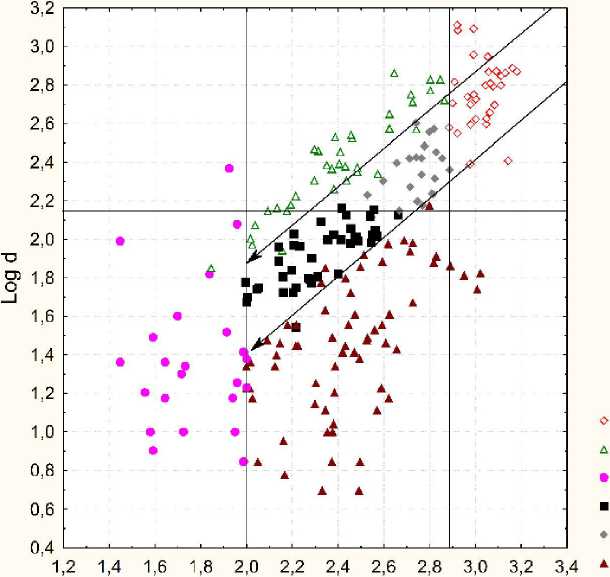
Важным является результат, представленный на совместной диаграмме рассеяния для двух признаков: логарифма длины материнского побега и логарифма максимальной длины бокового побега (см. рис. 6). Диагональные стрелки соответствую линиям постоянного отношения длины бокового и длины материнского побега. Они могут быть интерпретированы как линии постоянной формы ДПС. Вертикальные линии разделяют длину материнского побега на 3 интервала, соответственно, разграничивая типы ДПС. Горизонтальные линии на графике также разграничивают типы ДПС на два интервала по признаку максимальной длины бокового побега. Все три типа линий на диаграмме делят ДПС выборки по типам с надежностью более 97% (6 инверсий на 218 ДПС). Следовательно, для возрастного состояния G1 A. negundo действительно существуют 6 именно таких типов ДПС.

Кроме того, эти 6 типов ДПС разделяются всего по двум характеристическим признакам. Решающее правило2 представлено в табл. 6.

Log L

сверхростовая вертолет заполняющая основная ростовая расставка

Рис. 6 . Разделение ДПС на типы на основе двух признаков: логарифма длины материнского побега и логарифма максимальной длины бокового побега

Таблица 6

Таблица решающего правила по диапазонам двух метрических характеристик ДПС A. negundo в возрастном состоянии G1

Тип ДПС	Длина материнского побега, L (мм)	Макс, длина бокового, б(мм)	d/L
Заполняющие	L< 100
Вертолеты	100		2/3 < d/L
Расставки		d< 145	d/L < 1/4
Основные		d < 145	1/4 < d/L < 2/3
Ростовые	L < 760	d < 145	1/4 < d/L < 2/3
Сверхростовые	L > 760	d >145	1/4 < d/L < 2/3

Причины скопления точек около границ разных диапазонов на диаграмме рис. 5 могут иметь разную природу. Сдвиг по шкале логарифмов размера на определенную величину означает увеличение размера в соответствующее количество раз. Так, например, на рис. 5 нижняя граница размера материнского побега «сверхростовых» ДПС в 7,6 раза больше, чем соответствующая нижняя граница у «расставок», или чем верхняя граница «заполняющих». Отношение максимальной длины бокового к длине материнского побега d/L можно интерпретировать как характеристику формы ДПС. Логарифм этой величины равен разности показателей на осях диаграммы рис. 5.

Поскольку Л. negundo имеет накрест-супротивное листорасположение, последовательные пары боковых побегов расположены во взаимно перпендикулярных плоскостях. Это дает основания предполагать существенное влияние объема, занимаемого всей ДПС на ее строение. Для проверки значимости этого влияния был применен пошаговый дискриминантный анализ. В качестве предикторов были задействованы признаки логарифмов длины материнского побега L и максимальной длины бокового побега d, а также величина У= L d h как оценка объема ДПС, где h - длина максимального бокового побега в плоскости, перпендикулярной к максимальному по длине боковому побегу. Пошаговая процедура не включает признак V в модель дискриминантного анализа как признак с недостаточной значимостью по F-критерию. Трехмерность ДПС A.negundo по факту превращается в двухмерность.

На рис. 7 все типы ДПС представлены в соответствии серединами интервалов решающего правила из табл. 6.

2                ~

I" 3           4       5       6

Рис. 7 . Схематическое деление ДПС Acer negundo на типы по соотношению длины материнского и максимального бокового побегов: 1 -«основная», 2 - «вертолет», 3 - «заполняющая», 4 - «сверхростовая», 5 -«расставка», 6 - «ростовая»

Классический дискриминантный анализ как линейный статистический метод заведомо предполагает прямую пропорциональность вклада изменения каждого признака в итоговый эффект, в данном случае — дискриминантную функцию. В кибернетике, теории сложных систем, теории катастроф и ряде других дисциплин (см. напр., Арнольд, 1990), те явления, в которых этот принцип не применим, и небольшие изменения параметров приводят к значительным изменениям в системе, называют нелинейностью. В биологии мы постоянно сталкиваемся с ситуацией, внутренней регуляции (программы) процессов развития. Плавные изменения одного параметра приводят к принципиально разным состояниям системы, включая определенные пороговые механизмы. При этом сами диапазоны имеют резкие границы.

Именно программным характером роста побегов можно объяснить нелинейность процессов развития ДПС, приводящих к обнаруженной типизации. Доростание побега до определенного размера в определенных условиях вызывает включение новых механизмов роста. В связи с этим нет оснований предполагать адекватной как линейную модель, так и сопутствующие ей требования многомерного нормального распределения значений наблюдаемых признаков.

Заключение. Крона целого дерева в возрастном состоянии G1 впервые представлена системой ДПС. Все ДПС были типизированы по их трехмерному геометрическому контуру, который отражает сочетание большого набора признаков: линейных, угловых, временных и функциональных.

Состав дерева по выделенным типам ДПС напрямую связан с процессом формирования кроны как единого целого. Этот состав характеризует как возрастное состояние, так и условия роста дерева в конкретном местообитании.

Диапазон изменений внутри одного типа ДПС мал относительно общих диапазонов изменений метрических характеристик. Это следует из решающего правила, представленного в табл. 6 и видно на рисунках 5 и 6. При формировании типа действует пороговый механизм «все или ничего»: либо образуется ДПС одного из указанных шести типов, соответствующих узким диапазонам комбинаций состава коротких, средних и длинных боковых побегов, и плодов на материнском побеге, либо ДПС не образуется вовсе. Этот эффект обнаруживает присутствие программы, управляющей развитием дерева.

Геометрический контур ДПС A. negundo трехмерен и, с пространственной точки зрения, определяется признаками, не связанными между собой. Именно наличие некоторого плана, программы развития дерева делает признаки зависимыми и ограничивает количество вариантов их сочетаний при всевозможных реализациях ДПС на дереве. Из всего множества возможных сочетаний реализуются только шесть, они-то и являются шестью типами ДПС.

Одни и те же типы ДПС в одном возрастном состоянии обнаруживаются в разных частях ареала и различных местообитаниях. Раннее это явление уже было отмечено в работах (Антонова и др., 2012; Антонова, Барт, 2015; Антонова, Фатьянова, 2016) как свойство ДПС совпадать при наложении друг на друга.

При исследовании состава побегов на дереве медленный непрерывный рост размерных характеристик побегов в вариационном ряду являлся существенной причиной, затруднявшей их естественную типизацию (Barthelemy, Caraglio, 2007).

Невозможность произвольного сочетания разных метрических признаков на ДПС, разделение их на малое количество типов и легкость изменения количественного состава кроны по типам позволяют представить дерево, как модульную структуру. В такой структуре кроны двулетние образования оказываются минимальной пространственно-временной единицей, из которой складываются более крупные модули.

Еще ярче программа формирования ДПС проявляется в эффекте «кодировки». Разделение ДПС A. negundo на типы описывается с большой точностью линейными комбинациями пяти метрических признаков: логарифма длины материнского побега и логарифма максимальной длины бокового побега, количества коротких, средних длинных боковых побегов и количества плодов. С другой стороны, получено описание по более сложному правилу - но уже только двумя признаками: длиной материнского побега L и максимальной длиной бокового побега d. В итоге, двумя признаками L и d, кодируются остальные значения четырех признаков состава боковых побегов и плодов на ДПС.

Два признака кодируют реализацию сочетаний других признаков, которые являются более локальными и независимыми геометрическими характеристиками по отношению к этим двум.

Длина материнского и максимального бокового побега определяют основной геометрический контур, хотя сам геометрический контур ДПС A. negundo зависит от порядка расположения и длин боковых побегов, их углов ответвления, плодов, расположения на материнском побеге и т.д. Ранее нами было показано (Антонова, Барт, 2015), что из самых маленьких междоузлий побега образуются самые длинные боковые побеги.

Тот факт, что все получаемые типы ДПС кодируются только двумя метрическими признаками, говорит о большой строгости программы развития и жесткости связей всех участвующих характеристик. Именно структура кроны дерева предоставляет нам возможность зрительно зафиксировать эти соотношения.

Антонова И.С. Анализ метрических характеристик двулетних побеговых систем Acer negundo L. в молодом генеративном состоянии / И.С. Антонова, В.А. Барт // Вести. ТвГУ. Сер.: Биология и экология. 2016. № 4. С. 151-168.