Анализ моста, разработанного в соответствии с EN 1998-2

European standards provide common design rules for entire structures, as well as for their elements. The objectives of seismic design are explicitly stated: to ensure the protection of human lives, limit the damage of the structure and ensure the usage of facilities important for civil protection in the events of earthquakes. EN 1998-2 prescribes conditions that must be fulfilled in the design of bridges for earthquake resistance. [1] Their aim is to prevent a global failure of the structure in the events of strong earthquakes. In addition to the strength capacity, the appropriate ductility in the critical regions of the structural elements needs to be provided. It is not necessary for the structure to remain elastic under the influence of design seismic load. On the contrary, the development of significant inelastic deformations of the bearing members is allowed, provided that integrity of the entire structure is preserved. The basic concept presents a compromise between strength and ductility that is introduced through ductility classes and the use of behaviour factors, which is the main feature of EN 1998-1. [2]

Resistance and energy dissipation capacity depend on the extent of nonlinear response to which the structure is supposed to be introduced. The balance is established through the behaviour factor q and the corresponding ductility class. For dissipative structures, behaviour factor is adopted greater than 1.5, which introduces hysteresis dissipation of energy that occurs in specifically designed areas, known as dissipative zones or critical regions.

EN 1998-1 provides the possibility of using displacement based approach, through alternative design methods, presented in the informative annexes, for the calculation of target displacements for nonlinear static analysis (pushover). Prevention of the global collapse of the structure during strong and rare earthquakes is not achieved by designing structures for a higher level of seismic action, but imposing additional specific measures that need to be taken into account during the design process.

Based on the linear design approach, nonlinear deformations that will arise from the designed seismic actions cannot be determined, and thus, the damage proportions of the structure will also remain unknown. The comprehensive design approach includes nonlinear behaviour of the structural members at moderate and strong ground motions at the predetermined critical regions („Capacity Design” concept), which allows the dissipation of induced seismic energy. In addition to capacity, these sections must provide the appropriate ductility and deformation capacity. Required bending and shear capacity of the critical members needs to be fulfilled both in and out of the zone of the plastic hinge, and is accomplished by the appropriate arrangement of both longitudinal and transverse reinforcement. Nonlinear deformations of the structure can only be quantitatively determined through nonlinear analysis [3, 4].

Nonlinear static pushover analysis

Nonlinear static analysis (commonly referred to as „pushover”) is carried out under constant gravity loads and monotonically increasing lateral forces, which are applied at the location of the masses in the structural model to simulate the inertia forces induced by a single horizontal component of the seismic action. [5] Nonlinear static analysis is based on the determination of the force-displacement curve (capacity curve), relating the baseshear in the specific horizontal direction to a displacement of the representative point of the bridge in the same direction. The curve is constructed at least to a certain point of displacement, called the „target displacement“, which represents a component of the design seismic action in the horizontal direction of interest. During the construction of the curve, the order of formation of plastic hinges is followed, as well as the redistribution of internal forces in the bridge structure and the evolution of plastic hinge rotation demands. Assessment of the bridge behaviour for design seismic action is made upon the finite values of the plastic hinge rotation demands at the target displacement. Unlike elastic linear analysis or a nonlinear dynamic analysis, which results in the maximum response values for a given earthquake, pushover analysis provides only the capacity curve, and the demand needs to be determined separately, based on the maximum displacement of the reference point caused by the earthquake.

Models used for the analysis of ductile bridges should include the yield strength of ductile members and the post-yield monotonic branch thereafter. A ductile mechanism shows significant strength degradation by approaching the ultimate deformation from cyclic loading. However, deformation demands of the ductile members, due to the seismic actions, should be far less than the ultimate deformation [8-22].

Construction of Unique Buildings and Structures, 2014, №9 (24)

Target displacement for pushover analysis

Target displacement is defined as the seismic demand determined from the elastic response spectrum, through the displacement of the equivalent system with a single degree of freedom (SDOF). [6] Mass of the equivalent SDOF system m^* is determined as:

m * = 2 m i Ф i = 2 F i

while the transformation factor equals:

r =

* m

2 F i

2 m i ^ф i

У ( F 2 1

² m

V 7

Force F^* and displacement d^* of the equivalent SDOF system are calculated as:

F* = FL

Г

d * = d n

Г where Fb and dn are base-shear and displacement, respectively, of the control node of the multiple degree of freedom (MDOF) system.

Yield force F y ^* , which also represents the limit bearing capacity of an idealized system, is equal to the baseshear when formation of the plastic mechanism occurs. Initial stiffness of the idealized system is defined so that the area under the actual and idealized force-displacement curve is equal. Based on this assumption, yield displacement of the idealized SDOF system equals:

(

d

*

y

= ² d m

—

V

E

*

m

F * y 7

where E m ^* is the actual strain energy required for the formation of the plastic mechanism (Fig. 1).

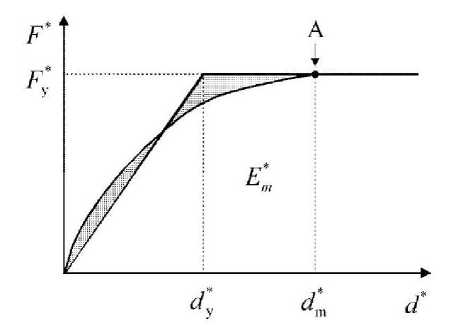
Figure 1. Idealized elastic-perfectly-plastic force-displacement relation

Period T* of the idealized equivalent SDOF system is determined by:

T = 2n

m d_y F y

Control displacement of the SDOF system for unlimited elastic behaviour equals:

Construction of Unique Buildings and Structures, 2014, №9 (24)

d

*

et

= S e ( Т *

T * 1 2

2 П

where S e (T^*) is the acceleration obtained from the elastic response spectrum for the period T^* . For T^* <  T C , target displacement is obtained from the following expressions:

If F y ^* / m^* ≥ S e (T^*) , response is elastic:

d t = d et

If F y ^* / m^* <  S e (T^*) , response is inelastic:

where q u equals:

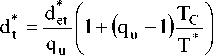
S e t m

F y^*

qu

For T^* ≥ T C , target displacement is obtained from the expression (8), where d t ^* should not exceed the value 3 d et ^* .

Target displacement for the MDOF system is finally determined as:

*

d t =r d _t

Numerical example – RC Girder Bridge with ductile columns of different height

A continuous three span reinforced concrete (RC) bridge structure, 15 + 25 + 15 m (55 m in total length), was analysed. In the central part, the beam is supported on columns of different height (14 m and 7 m), rigidly fixed into the foundations, while the beam ends are simply supported in the vertical and transverse direction.

Columns are of solid circular cross section, with a diameter of 2.0 m. A circular section has the same strength and rigidity in each horizontal direction, which makes it ideal for pier columns working as vertical cantilevers in both directions. Besides, it lends itself better than any other section to efficient confinement of the concrete and anti-buckling restraint of vertical bars – through circular hoops or a continuous spiral. [5]

Concrete quality is C30/37 and reinforcement S500 (class C) was adopted, with characteristic yield strength of f yk = 500 MPa. Structural model of the bridge, as well as the cross sections of the deck and columns, is presented in Fig. 2. The analyses considered using confined and unconfined concrete cross sections.

Due to the development of diagonal cracks, resulting from the main tension stresses, the torsion rigidity of the deck is reduced by 50 % of the homogeneous cross-section.

The main elements resisting seismic forces are the columns. A ductile seismic behaviour is selected for these elements, in accordance with EN 1998-2, and the value of the behaviour factor for the analyzed case is q = 3.5.

Structural analysis was conducted using the software SAP2000 v15.2.1. [7] Dynamic model of the deck consists of line finite elements, 2.5 m in length. Bridge mass is concentrated in nodes in proportion to the length of the segments.

The same reinforcement was adopted for both columns. The longitudinal reinforcement 64 0 25 (reinforcement ratio ρ = 1.0 %), determined for the shorter column (greater stiffness), is also adopted for the longer column, while the axial force of the two columns varies insignificantly. The transverse reinforcement is one spiral 0 16/70 (reinforcement ratio p = 1.2 %).

Force-based seismic design for ductility, using linear analysis for the 5 %-damped elastic spectrum divided by a reduction factor of elastic forces (the „behaviour factor“, q), implicitly assumes that the structure overall and those members in particular which develop inelastic deformations and ductility, have a nearly bilinear monotonic force-deformation behaviour, close to elastic-perfectly-plastic. Accordingly, the elastic stiffness used in the analysis should correspond to the stiffness of the elastic branch of a bilinear force-deformation response of the ductile members. When the actual monotonic force-deformation curve of a member expected to yield under the design seismic action is approximated as bilinear, the analysis should use as elastic stiffness the secant-to-yield point flexural stiffness. This applies in particular to columns in bridges designed for „ductile behaviour“ (i.e., q > 1.5). As far as the deck is concerned, which seismic design aims to protect from inelastic deformations and keep in the elastic range, the theoretical elastic stiffness of the full section is used, considering any concrete as uncracked.

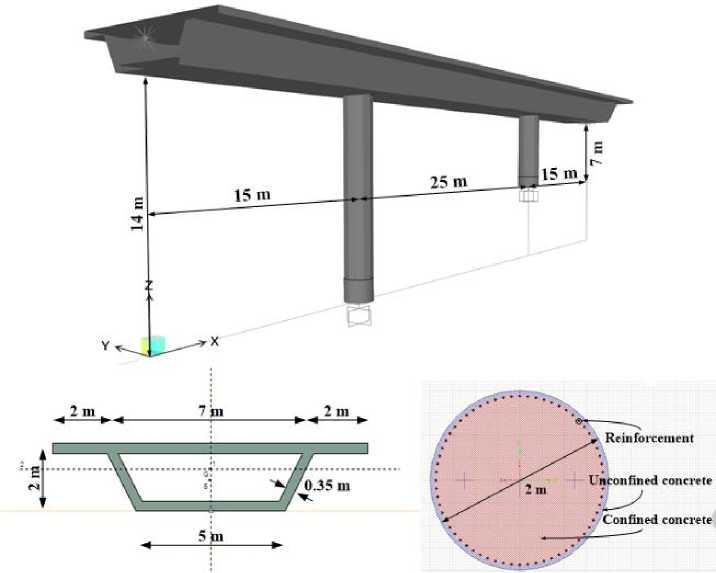
Figure 2. Structural model of RC Girder Bridge and cross-sections of the deck and columns

Modal analysis is conducted for modes that significantly contribute to the overall response of the structure, in this case, for the first five modes, which in the sum of effective modal masses capture more than 90 % of the total mass.

Approximate methods for estimating the second order effects can be used for critical regions (plastic hinges) in the linear analysis. Design effects are determined based on the combination of permanent and seismic actions.

Assessment of the structure behaviour is conducted by nonlinear static pushover analysis in the longitudinal direction. Two models are analysed. One with unconfined concrete cross-section (EN 1992-1-1) and the other with confined concrete cross-section (EN 1998-2) for the columns. Analysis was carried out with and without the effects of geometric nonlinearity (P-Δ effects). Forms of stress-strain relationships for confined and unconfined concrete are given in Fig. 3.

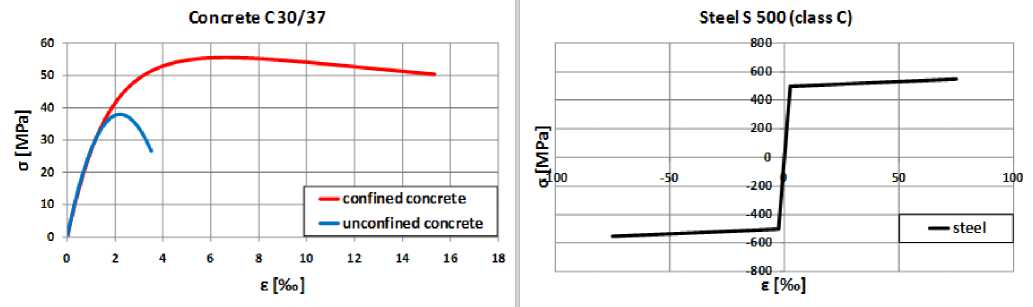
Figure 3. Stress-strain relationship for confined and unconfined concrete

Construction of Unique Buildings and Structures, 2014, №9 (24)

Numerical analysis results

Pushover curves for estimating the bearing and deformation capacity for the previously described models are given in Fig. 4.

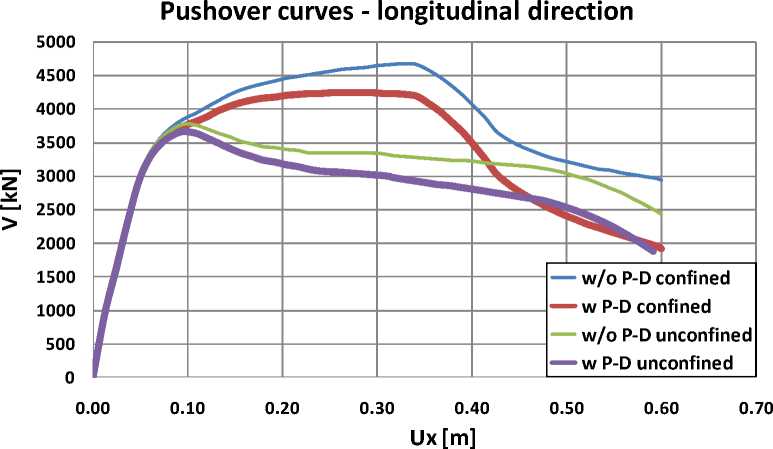
Figure 4. Pushover curves of the analysed models

Target displacements for design seismic actions, determined from the expressions (1)-(11) are given in Table 1. For the calculated displacements, strains in the compressed concrete marginal fibres and in tensioned reinforcement, for the shorter column, are also presented in Table 1. Based on the strains, the assessment of the achieved ductility is determined from the following expression:

µ=^{κ dt} κ y

where κ dt is the achieved curvature of the cross-section, and κ y is the yield curvature.

Table 1. Target displacements and the achieved ductility in the shorter column (7 m)

	Unconfined concrete		Confined concrete
	Without P-Д	With P-Д	Without P-Д	With P-Д
dt [cm]	9.3	9.4	11.3	10.5
ε b [‰]	-3.993	-4.079	-4.610	-4.153
ε a [‰]	13.6	13.8	18.7	16.7
d iv [m]	1.8998	1.8998	1.8749	1.8749
κ dt [m-1]	9.2604e-3	9.4110e-3	12.4327e-3	11.1222e-3
κ y [m-1]	2.3187e-3	2.3187e-3	2.4630e-3	2.4630e-3
μ [/]	3.99	4.06	5.05	4.52

Conclusion

Nonlinear response of the structure is expected for the design seismic action. In order to meet the nocollapse demand, it is necessary to estimate nonlinear deformations of ductile members in predetermined critical regions. Pushover analysis enables the construction of the capacity curve, which, for the target displacement, can be used to determine plastic hinge rotation demands.

Nonlinear analysis implies modelling nonlinear material behaviour of both concrete and reinforcement. In this paper, analyses were conducted for RC Girder Bridge with confined and unconfined concrete cross sections [1, 2] with and without the effects of geometric nonlinearity. Based on the pushover curves, it can be concluded that, for the same level of horizontal displacement, lower values of base-shear are obtained if P-Δ effects are applied. Obtained target displacement and achieved local ductility also differ whether concrete is modelled as confined or unconfined, giving higher values in favour of confined concrete.

Results are presented only for the shorter column. The cross section and the reinforcement are the same for both columns, but the stiffness, however, is different, being about inversely proportional to the third power of the column height. The shorter column will, thus, undertake larger seismic shears and develop higher design seismic moments, which will result in earlier yield and larger ductility demand in the plastic hinge. Longer, more flexible column remains in linear elastic response, as the achieved local ductility, in any case analysed, has values μ < 1 (yield curvature is not achieved).

Analysing the strains in concrete fibres and reinforcement, it can be concluded that the fail mechanism was not developed in either of the cases analysed.

Acknowledgements

The work has been done within the scientific research project "Theoretical, experimental and applied research in Civil Engineering", developed at the Department of Civil Engineering and Geodesy, Faculty of Technical Sciences, University of Novi Sad.