Анализ напряженно-деформированного состояния неоднородной пластической полосы

Введение. Существование участков конструкций из менее прочного (МП) материала является неизбежным следствием многих существующих технологий производства сварных соединений. Исследование возникающего в МП слоях и прослойках контактного упрочнения позволяет точнее оценить несущую способность неоднородных соединений, содержащих такие слои. В работе рассматривается дискретно-неоднородная полоса, состоящая из однородного изотропного идеально пластического материала, содержащая прямоугольную вставку из менее прочного материала, т.е. имеющего меньший предел текучести. Напряженное состояние полосы – плоская деформация, внешняя нагрузка – растяжение в направлении полосы. Результаты могут быть перенесены на упрочняемые материалы с заменой предела текучести на пластическую постоянную, характеризующую момент потери общей пластической устойчивости, так как в критическом состоянии поведение упрочняемого материала является близким к идеально пластическому.

При математическом моделировании напряжённо-деформированного состояния (НДС) МП слоя возникают недоопределённые краевые задачи для систем уравнений в частных производных гиперболического типа. Один из подходов к решению таких задач предложен и применялся в работах [1–3]. Он состоит из двух пунктов.

• 1.    Находится решение в окрестности свободной поверхности, где оно однозначно определяется граничными условиями, для чего вычисляются вдоль характеристик, точно или приближенно, инварианты Римана, с помощью которых решается задача сопряжения для напряжений на контактной поверхности. Найденные напряжения используются для вычисления критической нагрузки и для доопределения задачи из следующего пункта.

• 2.    Находится решение в окрестности поперечной оси симметрии слоя с использованием граничных условий на контактной поверхности, полученных в предыдущем пункте, и ограничений на классы решений на основе частичного предугадывания внутреннего состояния материала.

Естественным ограничением такого вида является гипотеза плоских поперечных сечений (ГППС) uy = W(у), где uy - скорость перемещения точек слоя в поперечном направлении. В работах [1–4] на основе ГППС проведено исследование НДС поперечного МП слоя полосы при растягивающей нагрузке в случае плоской деформации. Уточнением ГППС являются гипотезы, учитывающие прогиб плоских сечений при поперечном растяжении слоя uy = W(у) -(1 + ф(x, 5)), где ф - некоторая «малая» величина, характеризуемая малым параметром 5. Например, в гипотезе параболических сечений, использованной при математическом моделировании напряжённого состояния прослоек в стержнях [5], ф(x,5^) = ±5x2 (минус - при растяжении). При плоской деформации аппроксимация ф(x,5) = -5x2 не вполне удобна [6]. В работе применяется гипотеза ф(x,5) = -2sin2 ^2x, то есть предполагается, что uy = W(у) cos(5x). (1)

Цель работы - исследование напряжённого состояния МП слоя при гипотезе (1) и сравнение результатов с результатами, основанными на ГППС.

Нахождение приближенных зависимостей для напряжений на основе гипотезы (1). Как известно, НДС пластической среды при плоской деформации в безразмерных переменных определяется системой уравнений:

^д° х + ^{д т} ху д х д у ^д °у + ^{д т} ху д у д х

= 0;

= 0;

(°х- °у )2+4тху_ 4;

д v_x ^{д v} y а ^{+    _} 0;

дх   ду д vx °х - °у  ^Хх

^д v y ^д У

2 т       дv_x    ^д v_y "

xy x - + ' д у    д х

Функции, входящие в уравнения (2)-(6), определены на прямоугольнике [ - 1;1 ] х [ - к , к ] , где ке (0;1] - относительная толщина МП слоя. Введём обозначение:

Y ( у ) _ WM + 5 2 ''''■' W '( у )       W '( у )

•

Получим из условия (6) и гипотезы (1):

^т ху ^_ 4 55 ( ° х ^- ° у ) Y ⁽ у ^)tg^{( 5 x} ) •

Подставив полученное для т _ху выражение в (4), найдём:

°у - °х _±

4 ________

4 + Y ²( у )^tg2^ ^{5 X )} 5 ²

Г

_± 2 1 - - Y ²( у )

^ 8

tg (5х) +—Y\y)

5    128 ^{( у} )

tg⁴( 5 x )

54

... _j

(знак плюс соответствует растяжению соединения, знак минус - сжатию; в работе рассматривается растяжение). Отсюда

^Т ху

_ Y ( у )tg( 5 x ) - Y ³( у )tg³( 5 x ) + 3 Y ⁵( у )tg⁵( 5 x ) 256 5 5

1653

... •

При малых значениях касательных напряжений можно считать, что

^Т ху

_ Y ⁽ у ⁾tg^{( 5} x )

25

,

^ 1

° у ^- ° х ^{_ 2} ^ 1 ^- 8 Y ⁽ у )

tg^) j

•

Относительную погрешность в формуле (8) можно оценить величиной

0,125 т х ( 1 - 0,25 т ху )^{- 1,5}.

Например, если т _ху _ 0,3, относительная погрешность формулы (8) меньше 0,011.

Исключив из (2) и (3) нормальные напряжения, получим нелинейное уравнение относительно неизвестной функции т _ху :

д2 ,; ■, 8%.

д х д у

д X ²

д2т

—х^у _ о.

д У ²

Подставив сюда выражения (8) и (9), получим задачу:

Y " + 2 YY ' = 0, Y (0) = 0.

Результаты будут немного точнее, если количество слагаемых увеличить на одно, воспользовавшись равенством (7). После соответствующих рассуждений и преобразований аналог дифференциального уравнения (10) будет выглядеть следующим образом:

Y " + 2 YY ' - 5 ² Y = 0.                                 (11)

Аналитическим решением данного уравнения при начальных условиях Y(0) = 0, Y '(0) = A, где A – некоторая положительная постоянная, является функция:

+

Y ( y ) = Ath th( V Ay ) + ^ -j= sh ( 2 V Ay ) In |ch ( >TAy ) | - 2 y ch² ( JAy ) + -^= sh ( 2 A~Ay ) j 5 ² +

Г 2ln2 - 1     y +----- y +V=+ . A     V A	81             4ln2 2    3 2 + ln2( A 1) +        y + k 3               3 J
+ ^ 2 V A ln2 ^— + 2 AAA    з _	4 Г 4       2 о 12 , 8 ,2 1 о 16 j2 ^ 5 7 + — A ln 2-- A +-- A ln 2 +-- A y + k 15          5     15          5 J

Г i,²       5    ^

+7=

( V A  2 A V A J

sh ( 2V Ay ) - 2 A ch ( 2 y/Ay ) -^ — V_ + -^ y J th ( A Ay ) • ch ( JAy ) 5 ⁴ +.... (12)

При малых значениях касательных напряжений можно считать, что

_ V A th(V Ay ) tg( 5 x )

Txy =     2        5"'

Численные эксперименты показали, что решение (12) и решения уравнений (10) и (11) при условиях Y (0) = 0 и Y( к ) = b при различных подходящих значениях к и b мало различаются

(рис. 1). Поэтому точность основанных на уравнении (10) решений достаточна для приложений и позволяет получить не слишком громоздкие аналитические выражения в силу простоты решений задачи. Общее решение задачи (10) имеет вид

Y = V A th ( AAy ) .

Формулы (8) и (9) при 5 ^ 0 обращаются в известные зависимости [7, 8]:

^T xy = 2 x^A ^th (V Ay ) ;

^ y ^- ^ x = ² ( 1 ^- 8 x ² A ^th 2 ( "TAy ) J .

Пусть наибольшее значение TF касательных напряжений Txy достигается в некоторой точке F с абсциссой xF на контактной поверхности, которая задается уравнением y = к. Постоянная A находится из граничного условия t(xF ,к) = tf . Тогда для вычисления A следует решать трансцендентное уравнение

AA к th (AAK= = 25тFK . (     )  tg (5xf )

Введём обозначение. Пусть y = athd( x ) - функция, обратная к функции x = y th y . Для малых значений аргумента эта функция хорошо аппроксимируется функцией

V(x) = x+ + "4"x2 , которая на отрезке [0; 1] даёт ошибку в несколько тысячных. Тогда уравнение (14) можно записать в виде

Г ²⁵T F ^к )

I tg ( 5 xf ) J"

A = —a th d к

В работах [1-3] получены явные зависимости величин TF, GF и xF от параметров к и K, где K – коэффициент механической неоднородности, т.е. отношение пределов текучести более прочного основного материала полосы и материала менее прочного слоя. Используя их, можно находить коэффициент A. Например, при к = 0,3 и K = 1,3 значение параметра A = 5,0024.

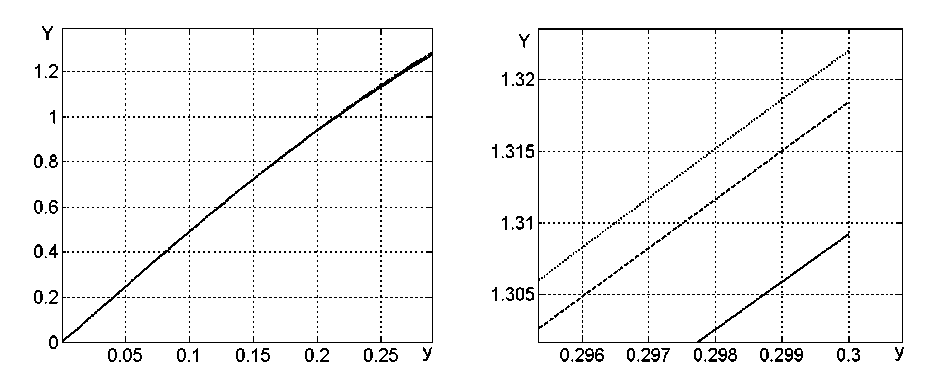
Рис. 1. Графики решения краевых задач для уравнений: (10) – сплошная, (11) – штриховая; график функции (12) – пунктирная; к = 0,3 , K = 1,3 , у е [ 0;0,3 ] (справа - увеличено в окрестности значения у = 0,3 )

Из уравнений равновесия (2) и (3) и формулы (13) интегрированием получим:

A ln|cos (Sx )|   ^ln| ch ( 4Лу )|

' = М21ь2р4У)      2

ln|ch (-jAy )| A ln|cos (Sx )| ay =--!—? +---!—a---1 + 2 + C .

2cos2 (Sx)

Использование условия пластичности (4) вместе с полученным в [1-3] значением GF позволяет найти постоянную C :

^ln| ch/ A v    A ln|cos ( S xf )|               ( K - 1 )( 3 - K )

C = aF +--——---7--!--------L - 2 , OF = 2 +  ----^-

2cos2 (SxF)       2S22

На рис. 2 показаны эпюры напряжений на контактной поверхности при гипотезе сечений данной работы при S = 0,5 и ГППС. Видно, что математические модели НС на основе ГППС практически не уступают по точности вычисления напряжений моделям, более детально учитывающим особенности деформирования МП слоёв.

Выводы. Уточнение ГППС в виде гипотезы деформирования плоских поперечных сечений (1) не дает ощутимых преимуществ в точности получаемых результатов. Если при нахождении зависимости касательных напряжений от координат использовать лишь первый член разложения в степенной ряд (формула (8)), допускаемая относительная ошибка при напряжениях, реально возникаюших в неоднородных соединениях, не превышает 0,01. Эти соображения позволяют находить достаточно точные

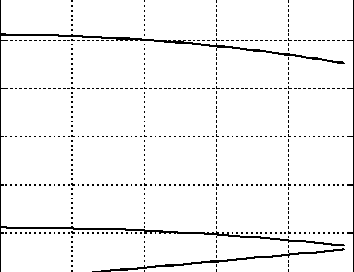
0                                     I                                   1-----------------------------------1-----------------------------------1--------------------------------

О          0.1          0 2          0.3          0 4 X

Рис. 2. Зависимость напряжений a y , y _x, T xy от x (сверху вниз) на контактной поверхности для значения S = 0,5 при к = 0,3 , K = 1,3

приближенные аналитические выражения простого вида для вычисления напряжений как функций координат, например, формулы (15)–(17).