Анализ некоторых особенностей развития поля скоростей в случае плоского течения жидкости, реологическая модель которой учитывает поперечную вязкость

В гидродинамике наряду с так называемыми ньютоновскими жидкостями, динамическая вязкость которых является постоянной, рассматриваются также нелинейно-вязкие неньютоновские жидкости с более сложными реологическими моделями.

При этом нельзя исключать возможность изменения реологической модели поведения жидкости в зависимости от уровня второго инварианта тензора скоростей деформаций или в частном случае скорости сдвига демонстрируют самые разные вязкие среды. В этой связи нередко предполагается, что динамическая вязкость описывается разными функциями на разных интервалах изменения второго инварианта тензора скоростей деформаций или, опять же, в частном случае скорости сдвига [1-9].

В данной работе предлагается реологическая модель подобной структуры (с различным поведением жидкости на различных интервалах изменения второго инварианта тензора скоростей деформаций), но применительно к поперечной вязкости. При этом за основу такой модификации принимается классическая модель Рейнера - Ривлина [6] с постоянным значением поперечной вязкости.

На основе предложенной реологической модели проводится анализ некоторых особенностей развития поля скоростей в окрестности рассматриваемых точек области течения для жидкости, реологическая модель которой

учитывает проявление эффекта поперечной вязкости при превышении вторым инвариантом тензора скоростей деформаций некоторого порогового критического значения.

Реологическая модель . Введем в рассмотрение реологическую модель вязкой несжимаемой жидкости в соответствии со сле-

дующими соотношениями

ту = -P5y + 2М£у + 4П(I2)Z6-к;    (1)

к = 1

^e ij =

I ₂

1 d Vj ^д v j +

2 5 x , d x i

i , j = 1, 2, 3;

= ^е 11 ^е 22 ^{+ 6} 22 ^ 33 ^{+ e} 33 ⁶ 11   ⁶ 12   ^S 23   ⁶ 31 ^;

n ( I 2 ) =

?;

_ n 0 ;

I 2 <  I 2 n ^;

I 2 >  I 2 n ^;

1_{2 n} >  0 - const; ц - const,

где T ij , e j - компоненты тензоров напряжений и скоростей деформаций; P - давление; S ij - символ Кронекера; ц - динамическая

вязкость жидкости; v _j - проекции скорости на направления координатных осей декартовой системы отсчета; X j - координаты; n ( 1 2 ) -поперечная вязкость жидкости, представленная в виде кусочно-постоянной функции второго инварианта тензора скоростей деформаций 1 2 ; 1 2 n - некоторое критическое значение второго инварианта тензора скоростей деформаций.

Жидкость с такой реологической моделью в той части области течения, где выполняется условие | / 2, <  1 2 п , ведет себя, как традиционная ньютоновская жидкость. В другой же части области течения, где выполняется обратное условие | / 2, >  1 2 п , сплошная среда проявляет свойства жидкости Рейнера - Ривлина [6].

Постановка задачи. Определяющие уравнения. Пусть в некоторый, условно принимаемый в качестве начального, момент времени в рассматриваемой области сформировалось плоское течение, поле скоростей и распределение давления в котором удовлетв оряют уравнениям Навье - Стокса [10] для классической ньютоновской жидкости с постоянным значением динамической вязкости ц независимо от конкретного распределения значений второго инварианта тензора скоростей деформаций (в смысле возможного превышения ими уровня 1 2 ^ ). Рассмотрим вопрос о том, как в дальнейшем может эволюционировать такое распределение скорости и давления в малой окрестности некоторой точки, начиная с начального момента времени, при условии, что в этой точке и ее малой окрестности выполняется неравенство | / 2, >  1 2 п • Последнее условие означает, что, начиная с начального момента времени, “включается” в соответствии с реологической моделью фактор поперечной вязкости.

Введем декартову систему координат, расположив ее начало в рассматриваемой точке. При этом ось 0x 1 сориентируем по касательной к линии тока, а ось Ox ₂ - по нормали к ней.

Если считать, что линии тока являются достаточно “гладкими”, то в малой окрестности рассматриваемой точки (начала координат) в начальный момент времени поле скоростей v ( x i , x 2 ) в первом приближении можно считать одномерным. Что же касается давления p ( x 1 , x ₂) , то, опять же, в первом приближении (по аналогии с одномерными течениями вязкой ньютоновской жидкости) можно считать его зависящим лишь от продольной координаты. Иначе говоря, в малой окрестности начала координат должны выполняться условия:

при t = 0; v _i = и ( x ₂ ) ^; v ₂ = 0 ^; p = P ( x _i) ,⁽²⁾

где и ( x ₂) , p ( x 1 ) - заданные функции соответствующих координат, которые удовлетворяют уравнениям Навье - Стокса для ньютоновской жидкости и условию неразрывности.

Получим уравнения, описывающие динамику жидкости с реологической моделью(1) в малой окрестности рассматриваемой точки и для малых моментов времени, непосредственно следующих за начальным моментом времени. Будем считать, что для такой пространственной области и на таком временном интервале распределения скоростей и давления допустимо представлять в виде суммы начальных распределений этих величин и их малых приращений

V 1 ( t , x i , x 2 ) = и ( x 2 ) + U 1 ( t , x i , x 2 );

< v 2 ( t , x i , x 2 ) =           u 2 ( t , x i , x 2 );                ⁽³⁾

_ p ( t , x i , x 2 ) = P ( x 2 ) + p 0 ( t , x i , x 2 ).

Перейдем к безразмерной форме представления основных уравнений с учетом соотношений

U Рt

U' = —; P ‘ = —; p ₀ = А ; t' = —;

uS       pS       pst vj            uj            xj vj =—; uj =—;xj = т; ту =_;

us       us       As

• i , j = i, 2, 3;

us = U(0); ts = ps = p-uS, где us, Ls , ts, ts , ps - характерные и принимаемые в качестве масштабных величины скорости, расстояния, времени, напряжения и давления; p - плотность жидкости.

Здесь в (4) и далее верхним штрихом обозначены безразмерные величины.

Говоря о выборе масштабных величин для расстояния l _s и времени t_S , заметим следующее. В предлагаемой задаче рассматривается лишь начальная стадия течения в малой окрестности рассматриваемой точки (начала координат) и для достаточно малого (“стартового”) интервала времени. Принимая во внимание такую “неопределенность” задания пространственных размеров области течения и характерного времени протекания процесса, можно видеть, что ввести конкретные значения Ls и t_S традиционным образом представляется затруднительным. В этой связи линейный масштаб и масштаб для времени предлагается ввести в рассмотрение следующим образом:

LS _

ц- K

р- Us

dU Г d2U dx 2 I dx 2 V

L S _ Ц ^{- K u} S p- u S

+ 2 K 0 ]

dU ‘ dx 2

г д ² и 2

_v д x [d x 2

д ² u ‘ д x 2²

K _

| grad( T )|

| grad⁽² ц^р2 )|

;

x ₂ _ 0;

+ 2 K 0 ]

dU Г d²U

dx ₂ ^

dx2

;

x ₂ _ 0;

;

x ₂ _ 0;

T _ ^{p u} S

2 ,

где T - плотность кинетической энергии; K - безразмерный комплекс.

При таком переходе к безразмерным величинам комплекс K [11] представляет собой по смыслу локальное число Рейнольдса, характеризующее местное соотношение факторов энергетики потока и диссипации в нем. Здесь, естественно, предполагается, что в рассматриваемой точке соответствующие производные отличны от нуля.

В представленной задаче этот безразмерный комплекс через начальное распределение скорости потока в окрестности рассматриваемой точки (начала координат) может быть представлен следующим образом:

K _

р - U dU Г d²U

Ц dx 2 ^ dx 2 v

x ₂ _ 0

Другие варианты также нетрадиционного введения локального числа Рейнольдса, подобные безразмерному комплексу K , описаны в [12] со ссылкой на [13,14], а также приводят-сяв работах [15,16].

С учетом (1), (2) после перехода к безразмерным величинам уравнения динамики жидкости и условие неразрывности потока в малой окрестности рассматриваемой точки принимают вид

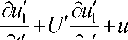
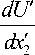
^д Р 0 e x

+--

K

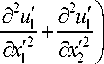
+ 2 - K 0

dU' Г д ² и ’ dx 2 ^5 x^x 2

д u ‘ _т „ ди ‘

—² + U '—² _

St'      d x ’

+--

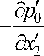
K

^д ² u 2 , d ² и 2 )

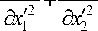
dU' d²U* dx 2 dx 22

d 2U*

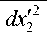
г д u ‘ д u ‘ ) —' + —2 If, ^дx2 дx‘ J

д u ‘ д u ‘ —1 + —2 _ 0 .

д x ‘ д x'₂

Здесь k ₀ представляет собой еще один безразмерный комплекс, характеризующий влияние поперечной вязкости и определяемый следующим образом [17]:

Kо _

П p L s

d ²U Г dU

dx 2

dx ₂

- 1

x ₂

_ 0

Следует отметить, что при выводе (5)-(7) принимали во внимание то обстоятель

ство, что начальные распределения скорости и давления в окрестности рассматриваемой точки тождественно удовлетворяют уравнениям Навье - Стокса с постоянной динамической вязкостью. Естественно, что при окончательной записи (5), (6) ограничивались лишь линейными членами по отношению к малым безразмерным приращениям скоростей и давления в (3).

В частном случае, когда поперечной вязкостью допустимо пренебречь либо она не проявляется в силу выполнения условия 1 1 2I <  1 2 п , имеем K о _ 0 . В такой ситуации уравнения (5)-(7) после традиционной процедуры исключения p 0 и перехода к функции тока сводятся к уравнению Орра -Зоммерфельда [18 - 20].

Анализ особенностей развития поля скоростей . Провести решение системы уравнений (5)-(7) для общего случая представляется затруднительным, в том числе и по той причине, что в рассматриваемой задаче о развитии течения в малой окрестности некоторой точки (начала координат) не совсем ясной является постановка граничных условий. Тем не менее можно получить некоторые результаты, касающиеся характерных особенностей в развитии поля скоростей на “стартовом ” периоде, непосредственно следующим за начальным моментом времени.

Поскольку речь идет лишь о некоторой малой окрестности рассматриваемой точки (начала координат), разложим безразмерные приращения скоростей и давления здесь в ряд по степеням координат и представим их в виде

№ № uk (t‘, x', x2) II wk, n, m (t') x nx2m;            (8)

n = 0 m = 0

k = 1, 2 ;

№ №

P 0 ( t ‘ , x ‘ , x 2 ) II q n , m ( t ') x ‘ n x 2 m ,              (9)

n = 0 m = 0

где w k , n , m ( t '), q n , m ( t ') - безразмерные коэффициенты в разложениях (8), (9), представляющие собой неизвестные функции времени.

Кроме этого разложим функцию и '( _х 2 ) в ряд по степеням поперечной координаты в окрестности рассматриваемой точки

№

U ‘ ( x 2 ) = I u m x 2 ^m ,                   (10)

о = 0

где U m - известные коэффициенты разложения.

Говоря о разложении типа (10), заметим, что в целом ряде известных профилей скорости (например, параболического профиля скорости для течения Пуазейля и некоторых других) количество слагаемых здесь может быть конечным.

Поскольку предполагается, что имеют место соотношения (2) и, следовательно, вначале с учетом (3) приращения скоростей и давления отсутствуют, то безразмерные коэффициенты в (8), (9) должны удовлетворять начальным условиям:

при / = ⁰; w k , n , m = 0;     q n , m = 0;

k = 1,2; n , m = 0,1,2,....                   (11)

Подставим (8)-(10) в систему уравнений (5)-(7). Тогда, выполняя соответствующие операции и приравнивая коэффициенты при одних и тех же степ енях координат в левой и правой частях соотношений (5)-(7), приходим к системе уравнений относительно функций w k , n , m ⁽ t ) ^и q n , m ⁽ t ^).

Сразу же укажем, что такая система уравнений не будет замкнутой. Ее замыкание следует проводить с привлечением соответствующих граничных условий, о сложности постановки которых уже говорилось выше.

Для примера приведем вид этой незамкнутой системы в случае, когда после соответствующих преобразований в (5), (6) допу стимо ограничиться лишь по одному уравнению, построенному на основе коэффициентов при нулевой степени координат

^1,0,0 .            ।                       ।

—dt;    + ^U 0 ^W 1,1,0 ^{+ U} 1 ^W 2,0,0 = ^- q 1,0 ⁺

2/

⁺ K ( w 1,2,0 ⁺ w 1,0,2 ) ^{+ 2} 0 ^U ( w 1,1,1 ^{+ 2} w 2,2,0 ) ^;

dw2,0,0   тт, ,    _    ,                     ,    \ dt,  + UО " w2,1,0 = q 0,1 + k ( w2,2,0 + w2,0,2 )

^{+ 2} K 0 {^2U1^U1 ^{+ U}1 ( ² w 1,0,2 ⁺ w 2,1,1 ) ⁺

⁺ 2 U_г ( w 1,0,1 ⁺ w 2,1,0 ) } ^;

^w 1,1,0 ⁺ w 2,0,1 = ^0;

• ²    w 1,2,0 ⁺ w 2,1,1 = ^0; w 1,1,1 ^{+ 2} w 2,0,2 = ^0.

Три последних уравнения здесь следуют из уравнения неразрывности (7).

Принимая во внимание (11), перейдем в получаемой системе к пределу при t' ^ 0. То гда приходим к следующим выражениям для начальных значений производных по времени от искомых функций, определяющих с учетом (8) распределения скоростей на “стартовом”

интервале времени,

<М, n , m

t = 0 ⁰

dw 2, n , m       ={ 0;     n = 1,2,3,...;

dt   t' = 0; [ Q m ;       n = 0;

n , m = 0,1,2,....;

Q m = 2 K , I k ( m + 3 - k )( m + 2 - k №+3-k .

k = 1

Будем полагать, что начальное распределение скорости (10) в окрестности рассматриваемой точки таково, что не все значения Q_m равняются нулю. Например, для часто встречающегося параболического профиля из (10) получаем

Q 0 = 4 K ₀ U ‘ U 2 ;    Q 1 = 8 K_aU 2² ;

Q m ^ 0; m = 2,3,......

Исключение составляют такие рассматриваемые точки, в окрестности которых начальный профиль описывается линейной функцией.

Таким образом, если для рассматриваемого начального профиля скорости хотя бы отдельные Q_m не равняются нулю, то производная по времени от поперечной составляющей скорости в начальный момент времени в окрестности изучаемой точки не будет тождественно равняться нулю.

Иначе говоря, при выполнении условия 1 1 21 >  1 2 n на “стартовом” временном интервале, непосредственно следующим за начальным моментом времени, в окрестности рассматриваемой точки будут “генерироваться” поперечные составляющие скорости, которые до этого здесь отсутствовали.

Если же начальное распределение скорости таково, что выполняется условие 1 1 21 <  1 2 n и К 0 = 0, то из (12) следует, что в начальный момент времени все производные обращаются в ноль. Это означает, что в такой ситуации не следует ожидать появлeния поперечной составляющей скорости.

Такое развитие поля скоростей для жидкости с реологической моделью (1) может интерпретироваться как начало перехода ламинарного режима течения в турбулентный.