Анализ панельных данных как инструмент сравнения региональных экономических систем (на примере регионов ДВФО)

Цель исследования состояла в том, чтобы проиллюстрировать возможность проведения сравнительного анализа региональных экономических систем Дальневосточного федерального округа (ДВФО) с использованием анализа панельных данных. Для анализа были использованы статистические данные по 9 регионам ДВФО в течение семи лет [2].

В данном случае не принципиально, за какой период времени бралась информация, так как цель статьи – показать, что панельные денные в принципе могут быть использованы для реализации поставленной задачи.

Перечень и нумерация регионов: 1 – Республика Саха (Якутия), 2 – Камчатский край, 3 – Приморский край, 4 – Хабаровский край, 5 – Амурская обл., 6 – Магаданская обл., 7 – Сахалинская обл., 8 – Еврейская автономная обл., 9 – Чукотский автономный округ.

Анализируемая информация изначально включала пять показателей, характеризующих экономику регионов: инвестиции в основной капитал, стоимость основных фондов, валовое накопление основного капитала, фактическое конечное потребление домашних хозяйств и валовой региональный продукт.

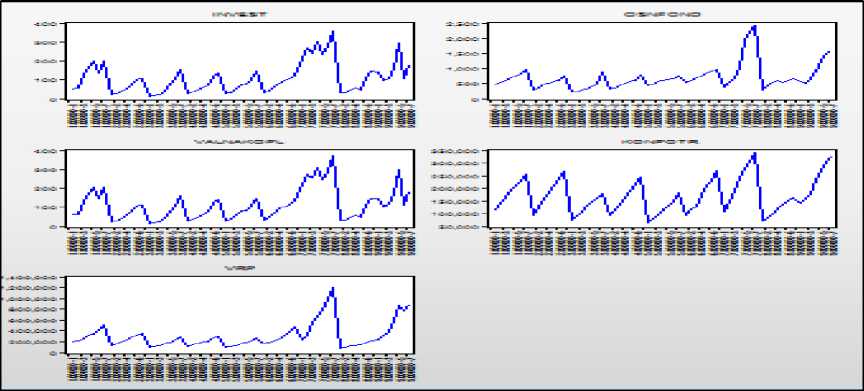
Рисунок 1 – Динамика анализируемых показателей (регионы – время)

Как видно из рисунка 1, динамика изменения этих показателей по годам и регионам совпадает, а матрица парных коэффициентов корреляции (рисунок 2) показывает, что показатели тесно связаны друг с другом. Если моделировать зависимость конечного потребления от остальных признаков, получим, что регрессоры являются мультикол-линеарными, то есть с информационной точки зрения дублируют друг друга, и часть из них при моделировании без потери точности модели можно будет исключить.

Covariance Analysis: Ordinary Date: 01/30/16 Time: 13:56 Sample: 1 7

Included observations: 63

Correlation Probability	KONPOTR	INVEST	OSNFOND	VALNAKO...	VRP
KONPOTR	1.000000
INVEST	0.713199	1.000000
	0.0000	—
OSNFOND	0.823653	0.734171	1.000000
	0.0000	0.0000	—
VALNAKOPL	0.721652	0.9 9 9445	0.740259	1.000000
	0.0000	0.0000	0.0000	—
VRP	0.874997	0.821592	0.9279 6 5	0.828468	1.000000
	0.0000	0.0000	0.0000	0.0000	—

Рисунок 2 – Матрица парных коэффициентов корреляции

Различные варианты сочетания признаков в регрессионном анализе показали, что более эффективно для решения поставленной задачи использовать анализ зависимости фактического конечного потребления домохозяйств от инвестиций в основной капитал и валового регионального продукта.

Как известно, модели панельных данных со случайными эффектами в большей мере подходят для анализа больших совокупностей на микроуровне, у нас же анализируются все регионы ДВФО (вся генеральная совокупность), а потому для дальнейшего анализа была выбрана модель с фиксированными эффектами с указанными выше регрессорами (рисунок 3).

Как видим, эта модель вполне подходит для дальнейшего анализа (довольно точная (R2=0,896), все оценки значимо отличны от нуля (prob для всех t-статистик < 0,05), и коэффициенты при переменных по знаку соответствуют их экономическому смыслу).

Тест Вальда (рисунок 4) показал, что модель с фиксированными эффектами более предпочтительна, чем обобщённая, (она указана в нижней части этого рисунка) так как вероятность для Chi-square, равная нулю, отклоняет гипотезу о том, что фиксированные эффекты отсутствуют.

Dependent Variable: KONPOTR

Method: Panel Least Squares

Sample: 1 7

Periods included: 7

Cross-sections included: 9

Total panel (balanced) observations: 63

Variable	Coeffici ent	Std. Error	t-Statistic	Prob.
INVEST	348.2501	88.60335	3.930440	0.0003
VRP	0.248 383	0.026 334	9.4321 1 9	0.0000
c	5537 0.94	8101.130	6.834965	0.0000

Effects Specification

Cross-section fixed (dummy variables)

R-squared 0.896152 Mean dependent var 1 69374.7

Рисунок 3 – Модель с фиксированными эффектами

Redundant Fixed Effects Tests Equation: Untitled

Test cross-section fixed effects

Effects Test                                Statistic            d.f.      Prob

Cross-section F                       8.163923       (8,52)    0.0000

Cross-section Chi-square            51.256049           8    0.0000

Cross-section fixed effects test equation Dependent Variable: KONPOTR Method: Panel Least Squares

Date: 01/30/16 Time: 16:23

Sample: 1 7

Periods included: 7

Cross-sections included: 9

Total panel (balanced) observations: 63

Variable	Coefficient	Std. Error	t-Statistic	Prob.
INVEST	-14.941 54	93.52017	-0.1 59768	0.8736
VRP	0.256685	0.031 635	8.1 1 3907	0.0000
О	91 956.95	7290.651	12.61300	0.0000
R-squared	0.76571 9	Mean dependent var		1 69374.7
Adjusted R-squared	0.757910	S.D. dependentvar		68462.1 4

Рисунок 4 – Тест Вальда для модели с фиксированными эффектами

Таблица 1 – Фиксированные индивидуальные эффекты по регионам

Номер региона	1	2	3	4	5	6	7	8	9
Величина эффекта	4 554	4 583	6 885	3 5607	-7 252	28 813	-87 719	3 505	-22 679

В таблице 1 показаны оценённые индивидуальные эффекты для каждого региона. Как известно, в этих эффектах отражена информация, не зависящая от времени и не учтённая в модели, то есть эффекты отражают индивидуальные особенности каждого региона.

По этим показателям видно, что регионы 1, 2, 3 и 8, а также регионы 7, 9 и 4, 6 могут иметь схожую структуру экономики, поскольку соответствующие фиксированные эффекты близки по величине и знаку. Отличается спецификой 5-й регион – Амурская область. Но это и понятно: специфика структуры экономики этого региона обусловлена высоким удельным весом сельского хозяйства, по сути, сельскохозяйственной специализацией.

Как известно, модели панельных данных не объясняют причину различия в индивидуальных эффектах, они лишь фиксируют наличие различий, и если эти различия присутствуют, то только потому, что это разные регионы. Тест Вальда «зафиксировал» такие различия, и мы можем считать, что экономики регионов различаются. Другой информации такие модели не дают.

Попробуем показать, что сведения о существовании различий можно подтвердить дополнительным анализом экономик этих регионов.

С этой целью для каждого региона за анализируемый период были рассчитаны темпы роста показателей зависимой и независимых переменных (по линейному тренду). Затем их сравнили, а именно то, во сколько раз темп роста регрессоров отличается от темпов роста зависимых переменных (таблица 2).

Таблица 2 – Сравнение темпов роста регрессоров с темпами роста зависимой переменной

Регион	1	2	3	4	5	6	7	8	9
vrp/konpotr	2,14	1,33	1,80	1,17	1,52	1,74	4,05	1,20	3,57
invest/konpotr	1,03	0,55	1,35	0,75	0,96	0,53	0,40	1.05	0,35

Как видим, валовой региональный продукт в этих регионах рос быстрее, чем инвестиции по сравнению с конечным потреблением, а инвестиции в основной капитал – значимо меньше. В этих показателях различия в структуре экономик не просматриваются. Рассчитаем отношения темпов роста регрессоров (vrp/konpotr) (таблица 3).

Таблица 3 – Сравнение темпов роста регрессоров

регион	1	2	3	4	5	6	7	8	9
Отношение темпов роста	2,08	2,42	1,33	1,62	1,53	3,28	10,15	1,14	10,2

В этой информации уже прослеживаются различия в структуре экономик регионов, и эти различия соответствуют различиям в индивидуальных эффектах. Так, величины эффектов первых четырёх регионов различаются незначимо, аналогично мы видим и в таблице 3. Аналогично в 7-м и 9-м регионах: у них индивидуальные эффекты значимо отличаются от таковых в других регионах (темпы роста валового регионального продукта в них существенно больше темпов роста конечного потребления, чем в других регионах).

Отдельная ситуация в 5-м регионе: отношение темпов близко к аналогичному отношению в 3-м регионе, но величины эффектов существенно различаются. Объяснить это можно тем, что экономики этих регионов существенно различаются по основной спецификации – Приморский край (прибрежный регион) и Амурская область (в основном сельскохозяйственное направление). Понятно, что точного соответствия в этих закономерностях искать не приходится, так как эти результаты получены на основе обработки выборочных данных статистическими методами, и различия могут быть уже в пределах статистических ошибок.

Подчеркнём ещё раз, что не следует искать в величинах индивидуальных эффектов причину различий в структурах экономик того или иного региона. Индивидуальные эффекты лишь фиксируют, есть ли различия в регионах и являются ли они значимыми. И если с их помощью зафиксировали, что один регион отличается от другого, то это лишь потому, что это другой регион. Какого-либо смысла в индивидуальных эффектах искать не сле- дует. Они лишь могут указать наличие или отсутствие индивидуальных различий. Выяснение причин таких различий следует искать в подробном анализе экономик этих регионов.