Анализ погрешностей численного решения задачи о распространении электромагнитного излучения в радиально-симметричном волноводе

Рассмотрим процесс распространения монохроматической электромагнитной волны в среде, который может быть описан следующим уравнением [1]:

д U     i

--1-- дz   2 ■ к ■ n 0

■A U - k-n^U ² ■ U = 0, 2 ■ n о ' '

где U - напряженность электрического поля, к -волновое число, n ₀ - показатель преломления среды, п_ш - изменение показателя преломления среды под действием поля распространяющейся волны, z - направление распространения волны.

Рассмотрим радиально-симметричный волновод, окруженный проводящей оболочкой. Для него уравнение (1) вместе с начальными и граничными условиями в цилиндрической системе координат примет вид:

д U     i

--1-- дz   2 ■ к ■ n 0

■A _rU - k-n^U |² ■ U = 0, ² ■ n о

<     0 <  r <  R , 0 <  z <  L ,

U z = 0 =V ( ^r ) , ⁰ <  ^r <  ^R ,

U r = R = ⁰, ⁰ <  z <  L .

Здесь R - радиус волновода, L - его длина, у ( r ) - функция, описывающая напряженность электрического поля на входе в волновод, а напряженность является функцией координат U = U ( z , r ) .

Далее рассматривается частный случай задачи, не учитывающий изменение показателя преломления под действием поля волны, то есть n_нл = 0. Также будем считать, что n ₀ = n = const .

Подставив в (2) волновое число к = 2 ^^ , где X - длина волны, и записав оператор Лапласа A _r в полярной системе координат, получим окончательную формулировку задачи:

д U X i ( д ² U 1 д U

--1---1-------2"" +--- д z   4 п n 15 r    r д r

0 <  r <  R , 0 <  z <  L ,

^\z = 0 =v ( r ) ,  ⁰ <  r <  ^R ,

U r = R = ^{11 0} <  z <  L ,

д u   X i д ² u  .

---+--- _r = 0, r = 0.

.д z   2 n n д r¹

Построение разностной схемы

Построим разностную схему для решения (3). Запишем для этого простейшие явную и неявную схемы для уравнения задачи, используя вспомогательный узел на сетке [3].

Пусть hz = L K - шаг сетки по направлению оси волновода, K - число узлов сетки по этому направлению, их координаты при этом z* = khz, к = 0, K .

Пусть также h_r = RJ - шаг сетки по направлению, перпендикулярному оси волновода, J -число узлов сетки по этому направлению, их координаты при этом r j = jh_r , j = 0, J .

Тогда явная и неявная схемы примут, соответственно, следующий вид:

к •1

uU-u1-+C (oj+в )=0,

0,5 ■ hz к + и к+1 -и 2      , i-i + C j + в*-1 )= 0,(5)

0,5 ■ hz iX где C =--комплексный коэффициент,

4п n k kk к uj+1- 2uj + uj-1

^а j = ---------5-------- ,                       ⁽⁶⁾

hr в k

kk uj+1 - uj-1

2 r_jh_r

+ u

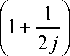
^{- u}* - 1

Ch z [ 1 2 h 2 I

-

1 J

2 j J

а u ^k_j – сеточный аналог искомой функции напря-

женности.

Из (4) и (5), добавив начальные и граничные условия, получим разностную схему Кранка-Николсона для исходной задачи (3):

^Uj h"^Uj + C ^ + j + в + j ) = 0, j = 1 J - 1, k = о, к - 1

e uj = Vj, j = 0, J k +1     k ( k+1     k+1      k k u 0 - u 0 , 9 J U1 - u 0   , U1 - u 0

+ 2 C          + hz ________I     hr           hr k = 0, к -1_

_ u J = 0, k = 0, K где v j = y V j ) .

Представим исходную задачу (3) и разностную схему (8) в операторной форме:

LU = f ,                                (9)

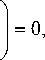
^L h ^u h = fh ■

Очевидно, что

f h

h ^ 0

f .

Нетрудно показать, что погрешность аппроксимации такой схемой исходной задачи будет:

||8 f h || = max { O ( h^h^), 0, O ( h^h^), 0 } . (12)

Очевидно, что

8 f h — 0.

Из (11) и (13) следует по определению, что разностная схема (8) аппроксимирует исходную систему (3) с порядком 2 относительно h_z и h_r .

Также можно показать устойчивость разностной схемы (8) [4].

Так как сходимость следует из аппроксимации и устойчивости, то построенная схема Кранка-Николсона (8) сходится, причем, как видно из (12), погрешность характеризуется выражением o (h 2 ,h 2 ) ■

Реализация разностной схемы

Рассмотрим алгоритм решения системы (8). Выделим в левой части первого уравнения системы напряженность электрического поля на слое k + 1, а в правой части – на слое k ; получим следующее выражение для j = 1, J - 1:

- k + 1 Chz h u1

j ¹ 2 h_r ² I

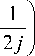
, £ + 1 1

+ U j | 1

-

hC I

1 + h_r ^{2 J}

k + 1 ^Ch z j ^{+ 1} 2 h 2

+ u ^k_j

-

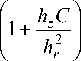
k   Ch z

^U j + 1 2 h 2

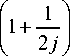
При k = 0 получим для j = 1, J - 1:

u

1   Chz j-1 2 hr

+ u

\ 1 - — J + u 1 1 1

I 2 j J j (

1 Ch z j ^{+ 1} 2 h r²

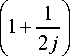
- u

0 11 hC + u "| 1 + -zy j |     hr2

-

u

hC I

7 J

+

Ch_z [ 1

2 ^ I

+

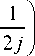
j - 1

0 Ch z j ^{+ 1} 2 h r ²

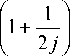
Значения функции u ( z , r )| z = 0 известны, т.е.

выражения в правых частях системы полученных уравнений можно считать величинами, зависящими только от индекса j :

d j =

-

^{- u} j - 1

Ch z [ 1 2 h ² I

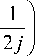
о [, h_zC

+ u " I 1 + -^y-

I      h_r ²

-

u "₊₁ ^Ch z -1 1 + —I , j = 1, J - 1. j ^{+ 1}2 I 2 j J’

Матрица коэффициентов правых частей системы уравнений относительно функции напряженности электрического поля представляет собой трехдиагональную матрицу, т.е. для решения данной системы уравнений можно применить метод прогонки.

Дополним систему уравнением для j = 0 (преобразуем третье уравнение схемы (8)):

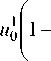
2 h_zC I 1 h ² I^{+ U} 1

nr J

2 Ch_z

h

2 r

= ^u 0 ^{1 1 +}

2 h z C J- _u 0

^{2 2 J} 1

r J

2 Ch_z

h r ²

0_ 0L 2hzCI   „2Chz d0 = u"I12T" I-U1 ,2 .                  (18)

(      h r J        h r

Используя краевое условие разностной схемы uJ = 0 для j = J -1, получим:

«¹ Ch z -11

^UJ - ² 2 h r I ¹

2( J - 1)

^{+ u} J - 1 ^{1 -}

h_zC _JI h r ^{2 J}J

- _U 0 ^Ch z [ 1

J - ² 2 h r C

-

2( J - 1)

0 [,    h_zC

^{+ U}J - 1 ^{1 +} "7T

|     h r

, (19)

d

J - 1

0 Ch z

— U r₂--т-

J ² 2 h r

1     1

2( J — 1) +

Аналитическое решение задачи

о |i h_zC I + u j -J 1 +у I .

I          2 I

V     "r J

Учитывая изложенные выше преобразования, получим следующую систему из J — 1 уравнений c J — 1 неизвестными, которая решается методом прогонки:

Для проверки корректности работы построенной разностной схемы найдем аналитическое решение системы (3). В данном случае это возможно сделать. Решим для этого следующее уравнение:

д U    X i f д 2 U 1 д U

11                    + дz 4тг I дr2 r дr

= 0 .                (24)

_u 1 ₀

2 h z C )

И Т J

+ U 1

2 Ch_z

^h r ²

= d 00

Решение будем проводить методом разделения переменных. Сделаем подстановку (25) в (24), получим (26).

U ( r , z ) = v ( z ) ■ w ( r )

1 ChzI, 1 I 1 I, U /-1 TI 1 —     I + U11 1 — j 12h2 V   2j J    j V

hC I

-Ц- I + hr ^{2 J}

v '( z ) 4 mi

■ v (z) iX

—П ^{f w} "^{( r )+ 1} w ^{,( r} w ( r ) V         r

i Ch li 1 I

< + u 1_+l — z -1 1 + — I = d 0 , j ^{+ 1}2 h ² V ² j J j’

j = 1, J — 1

Ch z I           1 I

I 1 I

J 2 2 h T V    2( J — 1) J

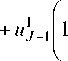
h_zC J h T J

= d

J 1

Решением уравнения dv (z) _ i^X dz ■ v (z) 4nn является функция:

I i X

^{v (} z ) = C 1 exp | p-— z

V 4 n n ,

Уравнение

Значение функции при j = J получим из краевого условия:

w "( r ) + — w '( r ) + p w ( r ) = 0 r

^u J = ⁰ ■

Нетрудно заметить, что матрица данной системы обладает диагональным преобладанием, что означает, что метод прогонки будет устойчивым.

Запишем общий вид системы на слое

к = 0, K — 1:

является уравнением Бесселя [5]. В данном случае его решение имеет вид:

^{w ( r} ) = ^J 0 ⁽V Y ■ ^r ) ■ ^C 2 ,                         ⁽³⁰⁾

где J ₀ ( x ) - функция Бесселя нулевого порядка [6]. Воспользуемся краевым условием:

w_r = R = C 2 J 0 (^ ■ R ) = 0                  (31)

„ k + 1 (t 2 hzC Y		, к + 1 2 Chz	d 0 ,
0 V2	h r J	u 1      h r 2
k + 1 Ch f	1 1 I	.    k +1 .	hzC 1
Ui 1 —z~	1--		—     +
j — 1 2 h 2 V	2 j J	j	h 2 J
+ u k + 1 C h z	f 1 +	1- d k ,
^     j + 1 2 h 2	V 2 j	J j ’	j ,      ,         (23)
k + 1 Ch (	1
Ui i —z"	1 —
J 2 2 h1; V	2( J	— 1) J
- +4, + UJ — 1 1 1 — V	h z C I = h2 J	d J—1 ,
_ u J + 1 = 0.

Решая методом прогонки систему (23) для к = 0, K — 1, получим значения функции напряженности электрического поля U на слое к = 0, к = 1 и так далее, каждый раз используя решение на предыдущем слое. Действуя таким образом, получим значения искомой функции напряженности электрического поля для всех узлов сетки.

Пусть у _k - нули функции Бесселя J ₀. Тогда

Pk = 4.

R

Таким образом, f X 2  1I

Uk(r,z)=Ck ■ exp1 hrY^z !■J01-xYk I■

V 4 n nR ² J   V ^R J

Тогда

U ^{( r} , ^z ) = E C k ■ ^e xp | i . ^X/ k 2 ^z ]■ ^J 0 ^f r Y k J ■ ⁽³⁴⁾ _k = 1        V 4 n nR ² J V R J

Воспользуемся начальным условием:

U\_z = 0 = V ( r ) = E C k ■ J 0 1- Y k l ■            (35)

k = 1        V ^R J

То есть Ck – коэффициенты разложения функции v(r) в ряд Фурье по базису функций Бес-

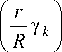
^k   R ² J 12 ( Y k )

j V ⁽ r ) ■ J 0 I ^- Y k \- r ■ dr ■      (36)

0         ^{V R J}

Реализация аналитического решения

Как видно из выражений (34) и (36), численная реализация данных выражений порождает ряд сложностей:

• 1)    численное нахождение значений у _k , J 0 и J ₁;

• 2)    численное интегрирование в (36);

• 3)    приближенное вычисление значения бесконечного ряда в (34).

Значения у _k являются табличными и могут быть взяты из справочников, либо рассчитаны с необходимой точностью [5, 6]. Для вычисления J 0 ( x ) и J । ( x ) могут быть использованы приближенные формулы необходимой точности [6].

Для общности применения реализации аналитического решения будем считать функцию у ( r ) заранее неизвестной и заданной не аналитически, а сеточным аналогом у j = у^ ) . Значения всех остальных подынтегральных функций в выражении (36) могут быть вычислены с известной точностью в любой точке, в том числе и в узлах сетки. Таким образом, это задача численного интегрирования, в которой невозможно увеличение точности за счет измельчения шага интегрирования (т.к. размер сетки задан заранее). Поэтому необходимо использовать метод интегрирования, дающий достаточно точный результат при заданном числе узлов. В данной работе использовались квадратурные формулы интегрирования Ньютона-Котеса порядка 11 [7].

Вычислить численно бесконечный ряд вида (34) при неизвестной заранее функции у ( r ) не представляется возможным, поэтому целесообразно заменить его конечной суммой первых W его членов:

меньше времени, затрачиваемом на вычисление значений функции напряженности.

Заметим также, что полученная оценка по грешности для UW (r,0) может служить оценкой по

грешности для U _W ( r , z )

т.к.

exp | i

Vk z J

4 n nR ^{2 J}

= 1.

Волноводы с неоднородным распределением показателя преломления

Рассмотрим волновод, распределение показа-

теля преломления которого неоднородно в направлении, перпендикулярном оси волновода. Заметим, что в уравнении (1) по-прежнему п_ш = 0, но теперь n ₀ = n ( r ) * const . Построенная нами разностная схема (8) применима и в таких случаях, потребуют-

ся лишь дополнительные вычисления при определении коэффициентов в системах в процессе решения.

Рассмотрим наиболее простой вид симметричного изменения показателя преломления n ( r ) , а

именно по параболическому закону:

n ² ( r ) = n ₁ ²

(          \2 I

1 — 2'(r J k a 7

k

где n ₁ – значение показателя преломления на оси волновода, а 5 и a являются параметрами изменения показателя преломления [2], причем 5 >  0 и 0 <  a <  R .

Рассмотрим случай, когда

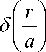
<< 1 .

Тогда (38) можно представить в следующем виде:

~ W             (   Xy 2    I  ( r   I

U W ^{( r} , z ) = Ё ^C k exp | i T^b- z I J 0 |      I . ⁽³⁷⁾

k = i       l   4 n nR²  J  k R    )

n ( r ) = n ₁

(     / \2 I

1 - AL J l a 7

.

k

Число W выбирается из соображений минимизации вычислительной погрешности, возникающей из-за увеличения числа операций, также не обладающих абсолютной точностью, при увеличении числа членов ряда, что приводит к накоплению ошибки. Заметим, что указанный выше способ вычисления значений функций Бесселя дает не совсем корректные результаты при неасимптотических значениях аргумента, что приводит к сильному ухудшению результата при увеличении количества используемых членов ряда.

В качестве критерия для выбора W могут служить вычисляемые значения U w ( r i ,0 ) , для которых известно точное значение у ( r ) . Оценка точности проводится по формуле А w = max У ( r ) - U w ( r ,0 ) . Тогда W = arg min A w .

i = 0, P ¹ w

Поиск минимума, вообще говоря, можно проводить любым способом, т.к. время, затрачиваемое на эту операцию при численной реализации, даже при неоптимальном способе поиска на порядки

Подставив (40) в (1), решим его методом разделения переменных:

U ( z , r ) = A ( r ) B ( z ) ,

B ' ( z )_ 1    A r A ( r )_ 2 ki B ( z )    n ( r )    A ( r )       Ц .	(42)
Решением уравнения
B ' ( z )- 2 ki B ( z )     M ,	(43)
очевидно, является функция
B ( z ) = C exp | — z J . k 2 k 7	(44)

Преобразовав второе уравнение из (42), получим:

d ² A 1 dA

—y- +---+ n dr2 r dr

( r ) ^ 4 = 0 .

Будем искать решение в следующем виде:

k

(

A ( r ) = X ( r ) exp ■

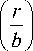
: I 7

В результате ряда замен переменных и преобразований, потребовав выполнения равенства

1 _ п ₁ ц8

b4 4a2 ,(47)

(это возможно в силу отсутствия ограничений на ц и b ), получим уравнение Лагерра порядка n ub21

m = —---

8     2 ,(48)

а решением его будет функция

/ х      Г 2г²)

X(r) = Lm I -pl,(49)

где Lm ( x ) - многочлен Лагерра порядка m [6].

Таким образом, решением уравнения (1) при условиях (38, 39) будет следующая функция:

отклонение сеточного решения от аналитического по модулю в квадрате в процентах относительно интенсивности максимального значения аналитического решения в этом слое ( z = z_k ).

Таблица 1. Результаты тестирования для решения (51)

n	X , мкм	R , мкм	L , м	hr , мкм	hz , мкм	%
1	0,63	50	0,1	1,5625	1,5259	0,14
1,5	0,63	50	0,1	1,5625	1,5259	0,14
1,5	0,63	50	1	2,5	15,259	0,38
1,5	0,63	150	10	6	152,59	0,23
1,5	0,63	1000	30	10	1000	0,01

Г 1 ц Y | 2 r^г

U = C exp z L I m

1 2 k ) I b ²

Г exp ^I

V

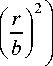
Экспериментальное исследование разностной схемы

Для проверки работы разностной схемы на вход волновода подавались различные распределения напряженности у ( r ) , а потом анализировались различия между аналитическим решением и решением, полученным с помощью разностной схемы.

Пусть у ( r ) = J 0 1 — y _m I , причем порядок корня v R   )

m зафиксирован. Очевидно, что решение примет вид:

Г

U ( r , z ) = exp i

v

x? m

4 n nR ²

)

z

)

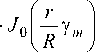
Заметим, что распределение интенсивности

U ² не будет зависеть от z и будет в точности сов-

падать с начальным.

Далее в таблице 1 приведены результаты тестирования работы разностной схемы при различных параметрах и m = 2 . В колонке «%» указано максимальное по всем узлам сетки отклонение рассчитанной интенсивности от начальной по отношению к максимуму начальной интенсивности, в процентах.

Проведем теперь исследование для реальной функции распределения:

у ( r ) = I ( r ) = P2- exp

Tia

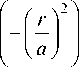
где P – мощность излучения, а a – эффективный радиус. Расчеты проводились для P = 0,5 и а = 0,1 ■ R . Результаты представлены в таблице 2. В колонке «%» указано максимальное по узлам сетки

Таблица 2. Результаты тестирования для функции распределения (52)

n	X , мкм	R , мкм	L , м	hr , мкм	hz , мкм	%
1,5	0,63	50	0,01	0,167	10	6,66
1,5	0,63	50	0,01	0,25	2	4,21
1,5	0,63	1000	1	5	200	0,57
1,5	0,63	1000	1	1,25	1000	0,01

Заметим, что до определенной степени эффект несовпадения решений удается нивелировать измельчением сетки по радиусу волновода: уменьшение шага сетки по радиусу h_r в 4 раза даже при увеличении шага сетки по длине h_z в 5 раз снизило погрешность вычисления на 2 порядка. Но подобный подход существенно увеличивает время расчетов и имеет предел, связанный с усилением вклада вычислительной погрешности при слишком мелком разбиении.

На рис. 1 показано распределение интенсивности напряженности электрического поля на выходе волновода при разных способах решения для следующих параметров: длина волновода L = 0,01 м, радиус R = 50 мкм, показатель преломления n = 1,5 , длина волны X = 0,63 мкм.

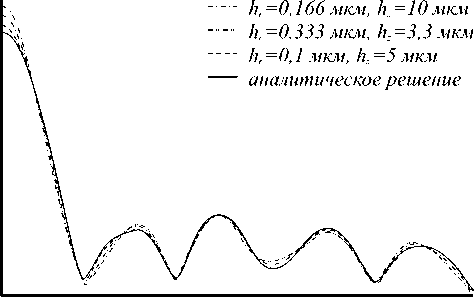
Рис. 1. Интенсивность напряженности электрического поля на выходе волновода

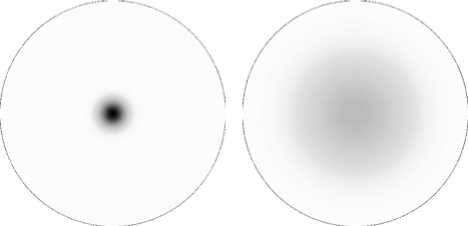
а) z=0

где Z i — один из корней полинома Лагерра L m ( x ) . Возьмем, например, i = 8, тогда Z 8 « 16,2792578313781. Далее в таблице 3 приведены результаты тестирования схемы при параметрах n 1 = 1,5; X = 0,63 мкм; a = 0,000025; L = 0,01 м; h_z = 10 мкм.

в) z=0,002

б) z=0,0008

г) z=0,01

Рис. 2. Интенсивность напряженности электрического поля в волноводе

Таблица 3. Результаты тестирования для модели волновода с неоднородным распределением показателя преломления

5	R , мкм	hr , мкм	%
0,1	49,219	0,164	49,056
0,01	155,644	0,519	19,123
0,001	492,19	1,64	0,121

На рис. 2 для этих же параметров показано изменение распределения интенсивности в процессе прохождения электромагнитного излучения по волноводу.

Для проверки работы схемы в случае волновода с неоднородным распределением показателя преломления естественно определить постоянную интегрирования в выражении (50) из начальных условий. Будем использовать в качестве начальных условий следующую функцию:

vVr ) = L m

( 2 r ² J l ь ² J

l

exp

^^^^^^»

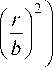
Очевидно, что при этом решение примет вид

и ⁽ z , r ) = exp l ^р z I L l 2 k I

f 2 r ² I m । b I exp

^^^^^^B

l

b J

I

Заметим, что в действительности не совсем корректно утверждать, что при заданных в таблице 3 параметрах выполняется равенство (55), т.к. оно было получено в предположении (39). Но условие (39) для первых строк таблицы 3 явно несправедливо, поэтому утверждать, что схема действительно дает погрешность по интенсивности такую, как указано в таблице, нельзя. Действительно, анализ графиков интенсивности электромагнитного излучения в волноводе показывает, что интенсивность в процессе распространения излучения по волноводу осциллирует около начального значения, при этом положение минимумов и максимумов напряженности примерно сохраняется.

Но уже для третьей строки таблицы 3 условие (39) выполняется, равенство (55) тоже, что и объясняет столь высокую точность вычислений.

Проверка порядка сходимости

Пусть Uh – сеточное решение при конкретных значениях hr и hz , а U – аналитическое с точностью выше, чем у сеточного. Погрешностью будем называть величину e = Uh -[U]hUh, (57)

U ( z , r ) ² = U ( 0, r ) ²,

где норма имеет вид:

то есть можно провести проверку разностной схемы по интенсивности электромагнитного излучения, как это уже проделывалось ранее для случая однородного показателя преломления в волноводе. Но для этого определим сначала ряд параметров.

Зафиксируем m , тогда из (47) и (48) определим ц и b ². Например, если взять m = 10, то

I ^hlu. = msxi k=0, K

V h .

Для рассматриваемой задачи должно быть справедливо выражение:

e = a h ² + в . + O ( h r2 , h z ) .                    (59)

И, вследствие (59), должно наблюдаться:

b ²

21 5 a ²

и

( 42 ) 2 ⁵

^р      2

ⁿ 1 ^a

Кроме того, для обеспече-

ния корректности краевых условий потребуем, чтобы выполнялось равенство:

lim e = e = P h 2

hr ^0 z z lim e = e = ah2

h z ^ 0

2 R ² b ²

Результаты исследования данных пределов приведены в таблице 4. Эксперимент проводился для параметров n = 1,5 ; X = 0,63 мкм; R = 50 мкм; L = 0,01 м; h z = 33,3 мкм; h r = 0,25 мкм и начально-

го распределения напряженности вида (52) с прежними параметрами. Отметим, что столь большие абсолютные значения погрешностей имеют причиной еще большие значения самой функции.

Таблица 4. Исследование пределов (60) для начального распределения напряженности вида (52)

hz , мкм	S z ( h z ) , 10 8	hr , мкм	s r ( h r ) , 10 9
25	8,96	0,1	1,059
8,34	3,52	0,05	1,046
4,17	2,68	0,033	1,044
2,08	2,46	0,025	1,043
1,78	2,44	0,02	1,042
1,31	2,42	0,016	1,042
1	2,40	0,014	1,042
0,66	2,39	0,0125	1,042

Результаты исследование величин а и в приведены в таблице 5. Эксперимент проводился для параметров n = 1,5 ; Х = 0,63 мкм; R = 50 мкм; L = 0,01 м; h z = 1,66 мкм; h r = 0,0083 мкм.

Таблица 5. Исследование параметров а и в в формулах (60)

hz , мкм	в ( h z ) 1018	hr , мкм	а ( h r ) , 10 21
25	1,215	0,1	3,86
20	1,465	0,05	4,05
16,7	1,617	0,033	4,2

Опираясь на данные, приведенные в таблицах 4 и 5, можно определить, что сходимость является квадратичной.

Заключение

В работе построена разностная схема для решения задачи о распространении монохроматической электромагнитной волны в радиально-симметричном волноводе, окруженном проводящей оболочкой, без учета влияния волны на преломляющие свойства вещества волновода. Также задача решена аналитически для двух случаев (в том числе для неравномерного распределения показателя преломления среды волновода), что позволило проверить корректность работы построенной разностной схемы. Результаты проверки показали, что данная схема вполне может быть использована для изучения процесса прохождения излучения через волновод. На расстояниях порядка 1 метра погрешность численного метода характеризуется величинами порядка 5%.

Работа поддержана грантом Президента РФ № НШ-1007.2003.1 и российско-американской программой «Фундаментальные исследования и высшее образование» («BRHE»).