Анализ полей напряжений в вершине трещины и параметры сопротивления разрушению в условиях градиентной пластичности
Автор: Хамидуллин Р.М., Федотова Д.В.
Статья в выпуске: 4, 2021 года.
Бесплатный доступ
Представлен численный анализ, основанный на ранее полученных экспериментальных данных по росту трещин для сталей Р2М и 34Х, алюминия 7050 и титанового сплава Ti-6Al-4V компактных образцов (CTS) с односторонним боковым надрезом, в рамках традиционной теории градиентной пластичности деформаций (CMSG), основанной на дислокационной модели Тейлора. В данном исследовании были рассмотрены начальные точки криволинейной траектории трещины для двух классических состояния: плоская деформация и плоское напряженное состояние при нормальном отрыве и чистом сдвиге. Конституционные уравнения поведения материала для теорий CMSGP были введены в вычислительный комплекс конечных элементов, и получены новые поля параметров напряженно-деформированного состояния для условий градиентной пластичности деформаций. Результаты FE-расчетов показывают значительное увеличение величины полей истинных напряжений в вершине трещины с учетом градиентов пластической деформации и внутренней характерной длины материала. Численные результаты также показывают, что сингулярность в области вершины трещины отлична для модели градиентной пластичности деформаций и зависит от формы разрушения I/II. Важным выводом относительно численных результатов в отношении параметров сопротивления разрушению материала, является то, что новые пластические коэффициенты интенсивности напряжений для градиентной пластичности отличаются для плоской деформации и плоского напряженного состояния, а также проявляют значительную чувствительность к пластическим свойствам материала и к масштабному параметру внутренней характерной длины, что является привлекательным с точки зрения практического применения и дальнейших фундаментальных исследований.
Градиентная пластичность, параметр сопротивления разрушению, плоская деформация, плоское напряженное состояние, нормальный отрыв, чистый сдвиг
Короткий адрес: https://sciup.org/146282376
IDR: 146282376 | УДК: 539.4 | DOI: 10.15593/perm.mech/2021.4.13
Analysis of stress fields at the crack tip and fracture resistance parameters under conditions of gradient plasticity
This paper presents a numerical analysis based on previously obtained experimental data on crack growth for P2M and 34X steels, aluminum 7050 and titanium alloy Ti-6Al-4V compact samples (CTS) with a one-sided lateral incision, within the framework of the conventional theory of strain gradient plasticity (CMSG), based on the Taylor dislocation model. In this study, the initial points of the curved crack trajectory were considered for two classical states: plane strain and plane stress with normal separation and pure shear. The constitutional equations of material behavior for CMSGP theories were introduced into the finite element computational complex and new fields of stress-strain state parameters for the conditions of strain gradient plasticity were obtained. The results of FE calculations show a significant increase in the magnitude of the true stress fields at the crack tip, taking into account the plastic deformation gradients and the internal characteristic length of the material. The numerical results also show that the singularity in the crack tip region is different for the model of gradient plasticity of deformations and depends on the mode I/II. An important conclusion regarding the numerical results regarding the parameters of the material's fracture resistance is that the new plastic stress intensity coefficients for gradient plasticity differ for plane strain and plane stress, and also show significant sensitivity to the plastic properties of the material and to the scale parameter of the intrinsic material length, which is attractive from the point of view of practical application and further fundamental research.
Текст научной статьи Анализ полей напряжений в вершине трещины и параметры сопротивления разрушению в условиях градиентной пластичности
ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2021PNRPU MECHANICS BULLETIN
В последние десятилетия все большее внимание ученых и специалистов обращено на поведение металлов на микроуровне, где эффекты градиентной пластичности проявляются на малых масштабах по отношению к структуре материала, что приводит к резкому локальному увеличению истинных напряжений. Проблема же состоит в том, что классические теории пластичности механики сплошной среды не в состоянии оценить эти микромасштабные эффекты, поскольку их конституционные модели не содержат внутреннего параметра характерной длины. Широкий спектр экспериментов на микроуровне, такие как кручение медной проволоки (Fleck et al., 1994 [8]; Guo et al., 2017 [23]) или изгиб и ограниченный сдвиг тонкой фольги (Stölken and Evans, 1998 [22]; Mu et al., 2014 [24]) показали, что металлы при нагружении выше предела текучести, проявляют сильные размерные эффекты, когда характерная шкала длин составляет порядка одного микрона. При этом градиенты пластической деформации возникают либо из-за неоднородной деформации материала, либо из-за способа нагружения. Таким образом, была сформулирована необходимость разработки новой общепринятой теории для обоснования масштабных эффектов и связи разрушения на микроуровне с атомистическими процессами разрушения в пластических материалах.
Первые теории градиентной пластичности были предложены Fleck and Hutchinson [3, 4] и Fleck et al. [5] для численного учета масштабных эффектов. Данная теория соответствует математической структуре теорий упругости с учетом членов высоких порядков с градиентами деформаций. Из необходимости соотнести размеры деформаций и градиентов деформаций был введен новый параметр внутренней длины l, который вводится в пластичность градиента деформаций и связан с плотностью дислокаций. Данный параметр рассматривается как внутренняя длина материала в зависимости от его микроструктуры, размер которой варьируется в диапазоне от десятой доли микрона до десяти микрон.
Теория Nix and Gao [1] частично прояснила смысл параметра внутренней длины материала l, введенного Fleck and Hutchinson [3], а также указала на необходимость дополнить градиентные теории пластичности экспериментальными законами на основе анализа доминирующих механизмов деформирования. Анализ Nix and Gao [1] основан на дислокационной модели Taylor [7], которая взаимодействует между сдвиговой прочностью и плотностью дислокаций в материале. Позже Gao et al. [2] дополнили формулировку более детальным анализом, которая получила название Mechanism-based theory of Strain Gradient plasticity (MSG). В MSG-теории полная плотность дислокаций считается через сумму статистической и геометрической составляющих, а сами эффекты градиентов деформаций становятся существенными, когда эти плотности имеют один и тот же порядок величины. Меньшие образцы приводят к наличию более сильного градиента деформаций и, следовательно, к более высоким плотностям геометрически необходимых дислокаций, поскольку напряжение потока зависит от общей плотности дислокаций. MSG-теория является прямой попыткой установить связь между механикой сплошной среды и атомистической структурой материала.
В 2004 г. Huang et al. [6] представили упрощенную теорию Gao et al. [2], обосновав и исключив из нее члены высоких порядков, связанные с ротационными составляющими, и эта теория получила название the Conventional Mechanism-based Strain Gradient (CMSG) plasticity. Данная теория низших порядков так же, как и MSG, основана на дислокационной модели Taylor. В CMSGP-теории градиент пластической деформации появляется только в конституционной модели поведения среды, а уравнения равновесия и граничные условия совпадают с традиционными теориями механики сплошной среды. Недавно Martínez-Pañeda [10] реализовал эту схему более низкого порядка для оценки градиентных эффектов, так как она не испытывает проблем сходимости в численном решении сложных задач механики трещин, в отличие от модели более высокого порядка (MSG). Также Martínez-Pañeda et al. [11–13] и Shlyannikov et al. [14–16] количественно определили соотношение между свойствами материала и характерным размером, на котором эффекты градиента заметно усиливают истинные напряжения в области вершины трещины. Исследования, проведенные в рамках феноменологических теорий и теорий, основанных на дислокационных механизмах, показали, что деформации вблизи вершины трещины способствуют локальному упрочнению и приводят к гораздо более высоким уровням напряжений по сравнению с классической теорией пластичности.
1. Конституционные уравнения теории градиентной пластичности
В настоящей работе использована упрощенная традиционная формулировка теории градиентной пластичности деформаций (CMSGP), разработанная Huang et al. [6]. Данная упрощенная модель пользуется большой популярностью благодаря своей более простой численной реализации, связанной с моделями более высокого порядка. Эффекты градиентов пластических деформаций проявляются через добавочный модуль пластичности, не требующий учета напряжений и граничных условий более высокого порядка. Таким образом, данная модель может быть реализована численно в качестве пользовательского материала с использованием стандартных формулировок конечных элементов. CMSG-теория пластичности, которая не включает в себя члены высоких порядков, основана на дислокационной модели Taylor, где градиент пластической деформации появляется только в конституционной модели, а уравнения равновесия и граничные условия такие же, как и в традиционных теориях континуума.
Согласно теории CMSG, соотношение между истинными напряжениями и деформациями при одноосном растяжении описываются как:
NN
, x E I ( CT.)
CT CT ref f (e p ) = CT y — Iе p + 1 , (1)
I cty J ( E J где ст ref является базовым напряжением при одноосном растяжении
CT ref =CT y ( E /CT y ) N , (2)
и f – безразмерная функция пластической деформации, определенная в результате аппроксимации кривой напряжение-деформация, которая представлена в виде степенного соотношения:
f ( = ' ) = ( = Р + ( ст,/ Е ) ) N . (3)
В уравнениях (1)-(3), ст y - предел текучести материала, N – показатель деформационного упрочнения, который изменяется в пределах 0 < N < 1.
В дислокационной модели Taylor [7] напряжение сдвигового потока т формулируется в терминах общей плотности дислокаций р как:
т = ац b Vp , (4)
где ц - модуль упругости при сдвиге, b вектор Бюргерса, а - эмпирический коэффициент, изменяющийся в пределах от 0,3 до 0,5.
Общая плотность дислокаций р состоит из плотности р s статистически сохраняемых дислокаций (SSD), которые накапливаются путем случайного захвата друг друга, и плотности р G геометрически необходимых дислокаций (GND), которые необходимы для обеспечения условий совместимости деформируемого материала:
Р = Р s + Р g • (5)
Плотность статистически сохраняемых дислокаций (SSD) связана с напряжением потока и кривой напряжения-деформации материала при одноосном растяжении
Р s =[ ст ref f (e P ) / M a P b ] • (6)
Плотность дислокаций геометрически необходимых дислокаций (GND) определяется неоднородностью пластических деформаций или градиентом эффективных пластических деформаций n P :
Р g = r П- , (7)
b где r – коэффициент Nye, величина порядка 1,90 для гранецентрированных кубических поликристаллов. Мера градиента эффективных пластических деформаций ПP введена в форме трех тензоров квадратичных инвариантов градиентов пластических деформаций, т.e.
П P = J n dt ; n P = j 411 Pk nP k ; г]pk = e P k J + e Pk , ,. - e P , k , ( 8) где e P - тензор скоростей пластических деформаций.
Напряжение течения при растяжении связано с напряжением при сдвиге потока, где M – коэффициент Тейлора, принимаемый равным 3,06:
n P
C flow = M T M a P b\ P S + r-r b
.
Так как градиент пластических деформаций n P при одноосном растяжении пропадает, то плотность дислокаций р s соответственно описывается уравнением (6), и напряжение течения можно представить в следующем виде:
C flow = C ref^ f 2 (е P ) + 1 П P ,
где l – характерная внутренняя длина материала, основанная на параметрах упругости ( ц ), пластичности ( с y ) и атомистическом расстоянии (вектор Бюргерса b ):
l = 18а2 ( ц/g y ) 2 b . (11)
Стоит отметить, что если внутренняя длина материала l значительно меньше характерного размера пластической деформации, связанной с GNDs, то l становится незначительным. Для металлических материалов внутренняя длина материала имеет порядок не более десятка микрон (Fleck and Hutchinson [3]). Важно отметить, что напряжения течения с flow и предел текучести с y являются различными характеристиками материала.
Для упрощения определяющих соотношений и исключения из рассмотрения терминов высоких порядков Huang et al. [2] предложили вязкоупругий аналог формулировки теории градиентной пластичности CMSG в виде следующих конституционных уравнений поведения материала:
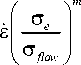
■
= е
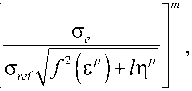
механизма (Gao et al. [2]), созданной на основе той же модели дислокаций Taylor. В результате было обнаружено, что распределения напряжений, предсказанные обеими теориями, различаются только в очень тонком слое толщиной около 10 nm. Упрощенная теория градиентной пластичности, основанная на механизмах деформации (CMSGP), как и другие теории пластичности сплошной среды, имеет нижний предел и не может быть использована для структуры нанометрового масштаба. Верхнего предела для применения CMSGP не существует, так как влияние градиента деформации l η p становится незначительным, поскольку данная упрощенная градиентная теория естественным образом переходит в классическую модель пластичности при увеличении характеристического расстояния l .
2. Объект исследования
В основе данной работы лежит ранее проведенное экспериментальное исследование компактного (CTS) образца с односторонним боковым надрезом [17]; были рассмотрены только начальные точки экспериментальной криволинейной траектории трещины в условиях нормального отрыва и чистого сдвига. Используемые компактные образцы (CTS) в данной работе выполнены из сталей P2M и 34X, а также алюминиевого Al-alloy 7050 и титанового Ti-6Al-4V сплавов. В табл. 1 приведены основные механические свойства материалов, где E – модуль Юнга, с 0 - предел текучести при монотонном растяжении, n – показатель деформационного упрочнения, N – показатель деформационного упрочнения, который изменяется в пределах 0 < N < 1.
Таблица 1
Основные механические свойства материалов
с у = Kе kk 5 у + 2Ц
^ ',
3е
2ч Чо e у flow
m
°- I Ci,
где с e - эквивалентные напряжения, Е д - девиатор скоростей деформаций, и m – экспонента, которая чувствительна к скорости деформаций.
Теория CMSG, как и в случае других моделей пластичности градиента деформации континуума, предназначена для моделирования коллективного поведения линейных дефектов кристаллической решетки и поэтому не применима в масштабах, меньше расстояния между дислокациями, которое составляет около 30 nm, так что напряжение потока в формуле (10) сохраняется в масштабе выше 100 nm. Huang et al. [6] сравнили упрощенную версию CMSG с теорией более высокого порядка пластичности градиента деформации на основе
Table 1
Basic mechanical properties of materials
|
Материал |
E (GPa) |
σ 0 (MPa) |
n |
N |
σ 0 / E |
|
Сталь P2M |
226,9 |
362,4 |
4,13 |
0,242 |
0,001597 |
|
Сталь 34X |
216,21 |
714,4 |
7,89 |
0,127 |
0,003304 |
|
Al-alloy 7050 |
70,57 |
471,6 |
10,85 |
0,092 |
0,006683 |
|
Ti-6Al-4V |
118,0 |
885,5 |
12,59 |
0,079 |
0,007504 |
При реализации данного численного исследования нами учитывались геометрия экспериментальных компактных образцов (CTS), широкий диапазон свойств материала и условия их нагружения (табл. 2), чистый режим разрушения I достигается в условиях, когда сила F прикладывается в направлении β = 90°, тогда как режим разрушения II реализуется путем приложения силы F в направлении β = 0° (рис. 1).
Основной особенностью данного исследования является оценка эффектов градиентной пластичности деформаций и влияния напряженно-деформированного состояния (плоская деформация и плоское напряженное состояние) при двух режимах разрушения I и II. Для этого
Таблица 2
Размеры образцов и условия нагружения
Table 2
Sample sizes and loading conditions
|
Материал |
Приложенная нагрузка F , kN |
Угол приложенной нагрузки α , º |
Толщина образца t , mm |
K 1 (MPa·m0.5) |
K 2 (MPa·m0.5) |
|||
|
mode I |
mode II |
mode I |
mode II |
mode I |
mode II |
mode I |
mode II |
|
|
Сталь P2M |
7,0 |
14,0 |
90 |
0 |
4,83 |
4,51 |
18,296 |
18,552 |
|
Сталь 34X |
7,3 |
14,8 |
90 |
0 |
5,04 |
5,05 |
18,287 |
17,516 |
|
Al-alloy 7050 |
2,8 |
11,0 |
90 |
0 |
4,85 |
5,01 |
7,288 |
13,122 |
|
Ti-6Al-4V |
5,0 |
17,0 |
90 |
0 |
5,0 |
5,02 |
12,624 |
20,239 |
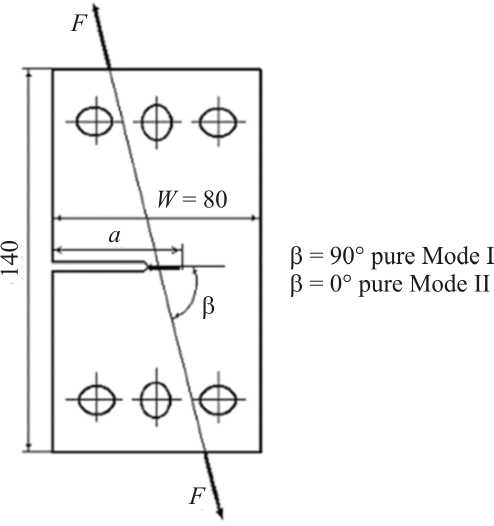
Рис. 1. Компактный образец (CTS)
-
Fig. 1. Compact Sample (CTS)
в расчетах значение внутренней характерной длины материала l варьировалось в диапазоне от 1 до 10 µm. Кроме того, в расчетах берега трещин для рассматриваемого компактного образца свободны от напряжений. Упругие коэффициенты интенсивности напряжений K 1 и K 2 приложены за счет монотонно возрастающей нагрузки.
Нами были сформированы конечно-элементные модели образцов CTS с односторонним боковым надрезом, которые имеют ширину W = 80 mm и начальную длину трещины a 0 = 40 mm, где начальная вершина трещины представлена с конечным радиусом кривизны ρ = 0,06 µm (рис. 2). Чтобы проиллюстрировать влияние градиента пластических деформаций вблизи вершины трещины использовалась высокоточная мелкоразмерная сетка конечных элементов повышенной плотности, в результате чего размер соответствующего конечного элемента у вершины трещины был равен h = 6 nm. Среднее количество элементов сетки конечных элементов составляет приблизительно 55 000.
Численные расчеты в рамках настоящего исследования выполнены с привлечением вычислительного МКЭ-комплекса ANSYS [25]. В частности, были реализованы определяющие соотношения (уравнения (1),
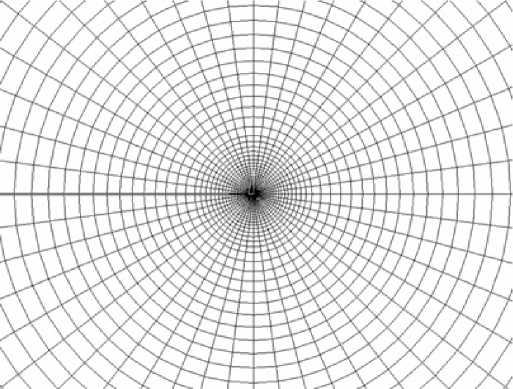
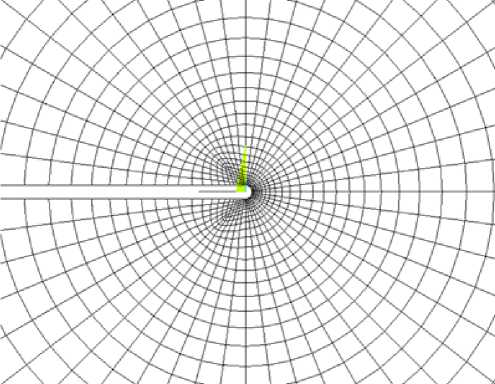
Рис. 2. Сетка конечных элементов в вершине трещины ( а ), вершина трещины с конечных радиусом кривизны ( б )
Fig. 2. Finite element mesh for the crack-tip problem (а), Near-tip mesh with the initial crack-tip radius (б)
3. Поля напряжений в вершине трещины
(12), (13)) градиентной теории пластичности CMSGP в программе конечных элементов ANSYS через пользовательскую подпрограмму USER-MATERIAL. Реализация теории CMSGP на основе механизма в комплексе конечных элементов была более подробно описана в работе Martínez-Pañeda et al. [11] и в статье авторов Shlyannikov et al. [16]. Модули языка программирования Fortran использованы для вычисления компонентов пластической деформации в точках интегрирования по Гауссу, а в результате численного дифференцирования внутри элемента вычисляется градиент пластической деформации.
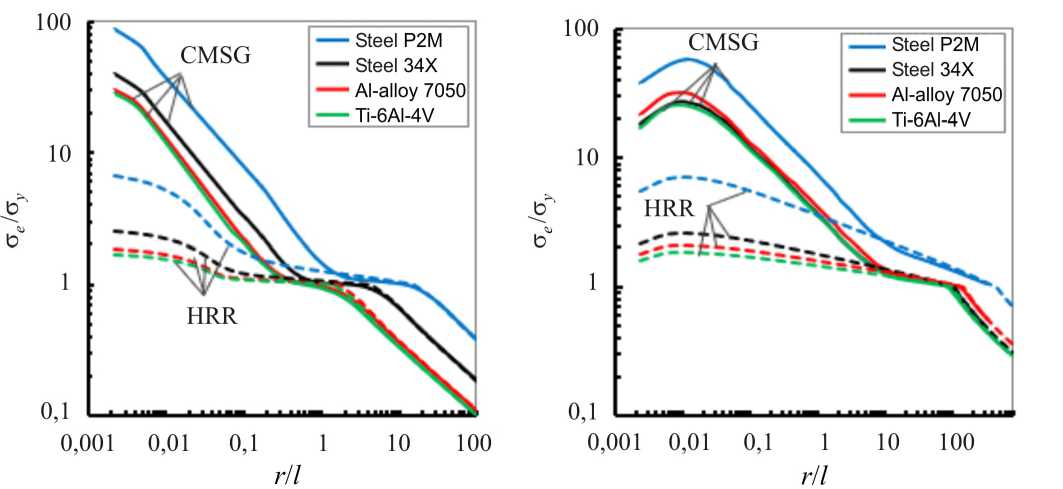
Результаты численных исследований в данном разделе придерживаются сопоставления поведения рассматриваемых параметров при плоском напряженном состоянии и плоской деформации для двух различных условий нагружения (чистый режим разрушения I и II). Для демонстрации эффектов градиентной пластичности в распределениях полей напряжений приведено сравнение с классической моделью пластичности в форме решения Hutchinson – Rice – Rosengren (HRR). Результаты расчетов (рис. 3) содержат радиальные распределения эквивалентных по Мизесу напряжений в плоскости расположения трещины, нормированных на предел текучести материала σ e / σ Y при плоской деформации в зависимости от нормализованного расстояния r / l , при заданном значении внутренней характерной длины материала l = 5 µm. Величина нормированных эквивалентных напряжений σ eqv σ Y = 1 соответствует границе между упругим и пластическим состоянием материала. Результаты расчетов полей напряжений для градиентной пластичности CMSG обозначены сплошными линиями, а для классической модели пластичности HRR-решение обозначено пунктирными линиями на рис. 3.
Из результатов, представленных на рис. 3, можно сделать вывод, что учет в конституционных уравнениях градиентной пластичности CMSG параметра характерной внутренней длины материала l приводит к увеличению значений эквивалентных напряжений σe /σY на порядок и более как при нормальном отрыве I, так и при чистом сдвиге (II). По мере удаления от вершины трещины (r/l > 0,3 для нормального отрыва I и r/l > 7 для чистого сдвига II) эффекты градиентной пластичности пропадают, и решение постепенно переходит к состоянию классической сингулярности типа HRR-решения. Углы наклона кривых распределений напряжений для градиентной пластичности CMSG и для классического HRR-решения заметно различны, что говорит о различном типе сингулярности в вершине трещины. Нормированные эквивалентные напряжения σe /σY имеют набольшее значение у стали Р2М (N = 0,242) и наименьшее – у титанового сплава Ti-6Al-4V (N = 0,079). Области расстояний 0,003 < r/l < 0,3 для режима разрушения I и 0,003 < r/l < 7 для режима разрушения II можно считать зонами доминантности градиентной пластичности.
На рис. 4 показаны различные вариации радиальных распределений нормированных эквивалентных напряжений σ e / σ Y в зависимости от нормализованных расстояний ( r / a , где а – длина трещины). Данные распределения представлены как функции параметра Тэйлора l , положенного в основу теории градиентной пластичности с учетом механизмов деформирования (CMSG). Сравнение эпюр радиальных распределений полей напряжений приведено для условий плоской деформации и плоского напряженного состояния для режима разрушения I ( а , в ) и режима разрушения II ( б , г ), при различных значениях характерной длины материала l = 1 и 10 µm. Из представленных данных видно, что действительно внутренний параметр характерной длины материала l является управляющим параметром конституционных уравнений теории градиентной пластичности. При величине l = 1 µ m распределения напряжений стремятся к ситуации почти идеальной пластичности, тогда как при l = 10 µ m состояние материала приближается к более упругому. Для режима разрушения I плоское напряженное состояние демонстрирует более высокие эффекты градиентной пластичности в вершине трещины по сравнению с плоской деформацией, в отличие от режима разрушения II, где поля напряжений практически одинаковы для обоих состояний. Еще одним заметным различием между режимами I и II является снижение эквивалентных напряжений вблизи вершины трещины в последнем. Данное разряжение распределения напряжений по мере приближения к вершине трещины происходит для сечения, совпадающего
а
б
Рис. 3. Распределение эквивалентных нормированных напряжений при ПД в чистом режиме разрушения I ( а ) и режиме разрешения II ( б ) при l равном 5 µm
Fig. 3. The distribution of equivalent normalized stresses under plane strain in the pure mode I ( a ) and mode II ( б ) at l equal to 5 µm
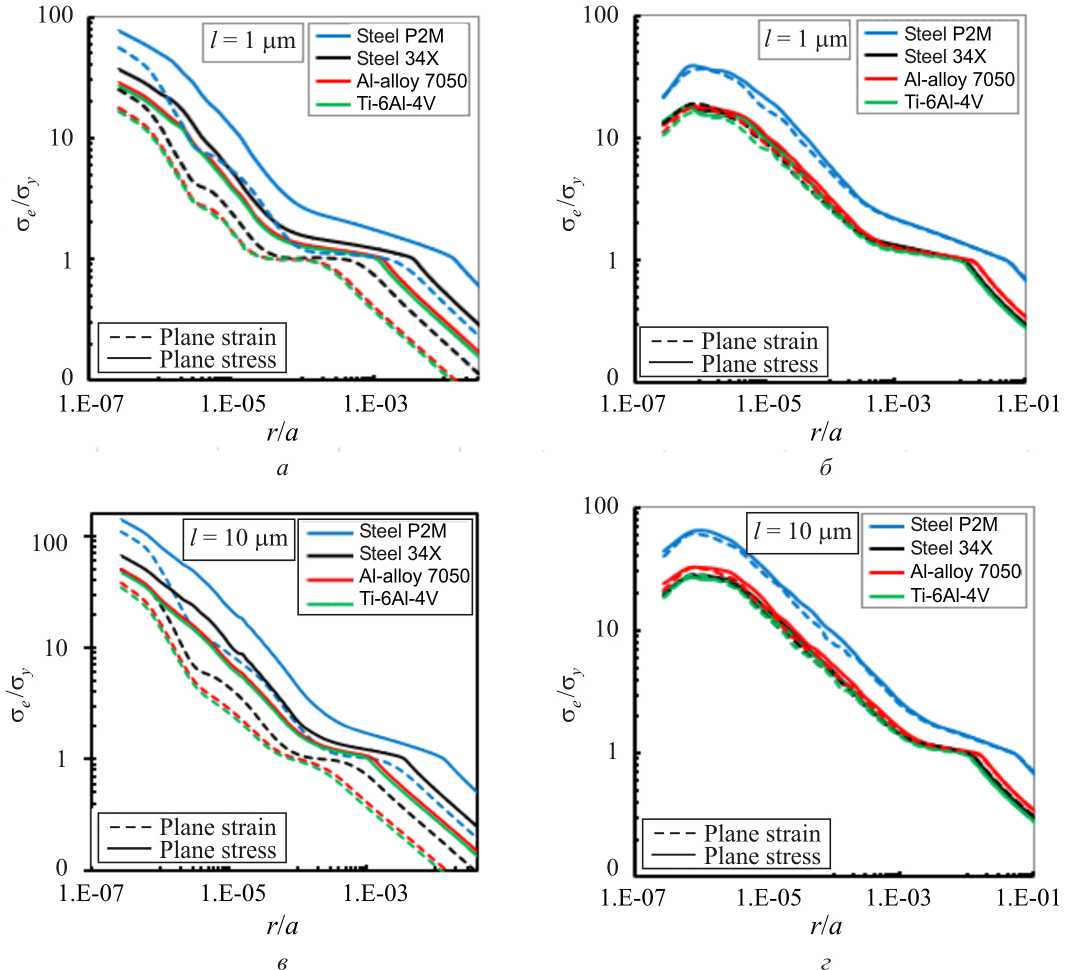
Рис. 4. Сравнение распределений эквивалентных напряжений при ПД и ПНС в чистом режиме разрушения I ( а , в ) и режиме разрешения II ( б , г ) при l равном 1 и 10 µm
-
Fig. 4. Comparison of the distributions of equivalent stresses under plane strain and plane stress in the mode I ( a , в ) and mode II ( б , г ) at l equal to 1 and 10 µm
с начальной плоскостью ориентации бокового надреза ( в = 0 ° ) в компактном (CTS) образце. Также стоит отметить, что более пластичные материалы, такие как титановый Ti-6Al-4V и алюминиевый 7050 сплавы, проявляют более сильное свойство чувствительности к изменению параметра внутренней длины материала.
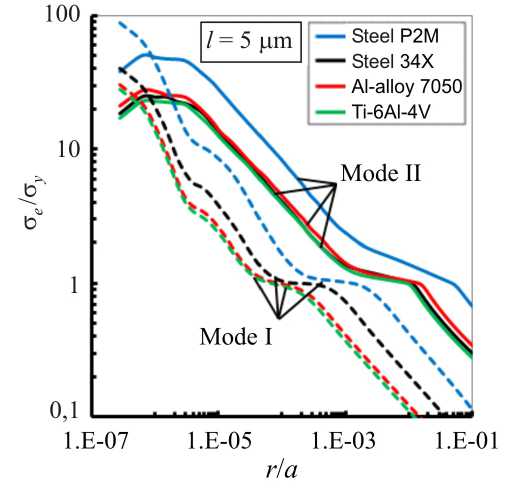
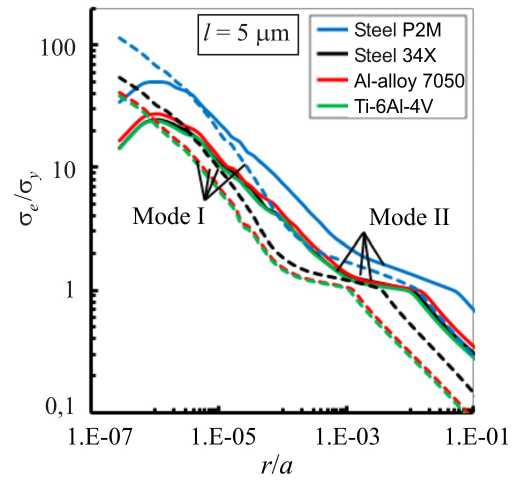
На рис. 5 показано влияние типа режима разрушения (I/II), пластических свойств материала и выбора напряженно-деформированного состояния при пластической обработке на эквивалентные нормализованные распределения напряжений вблизи вершины трещины при 0 = 0 ° в образцах CTS. На рисунке проиллюстрированы результаты обработки при параметре внутренней характерной длины l = 5 µm. Из данных графиков следует, что в условиях плоского напряженного состояния нормированные эквивалентные напряжения больше для режима нагрузки I по сравнению с режимом II. Однако в условиях плоской деформации нормализованные распределения эквивалентных напряжений режимов I и II кажутся довольно похожими. Тенденции, наблюдаемые на рис. 5, сохраняются для разных значений внутреннего параметра l (1 и 10 µm).
В табл. 3 приведены результаты определения типов сингулярности вершины трещины кривых распределения нормированных эквивалентных напряжений. По данным результатам можно сделать несколько интересных выводов. Во-первых, значения сингулярности вершины трещины для плоской деформации и плоского напряженного состояния в условиях режима разрушения I больше, чем значения, полученные для чистого режима II в эквивалентном напряженно-деформированном состоянии. Более того, типы сингулярности во всех случаях, включая режим II, больше, чем при классической линейной упругости. Таким образом, модели градиентной пластичности, основанные на дислокационной теории Тейлора, по-видимому, предсказывают более сильную сингулярность, чем линейные упругие твердые тела, как для плоской деформации, так и для плосконапряженного состояния в режимах разрушения I и II. Во-вторых, величина сингулярности напряжений проявляет некоторую чувствительность к изменению параметра внутренней длины материала l, причем данное свойство в большей степени проявляется при режиме разрушения II.
Теперь обратимся к анализу градиентного влияния на полярные распределения и изменения форм контуров безразмерных эквивалентных напряжений в образцах CTS.
а
Рис. 5. Сравнение распределений эквивалентных напряжений в чистом режиме разрушения I и II при ПД ( а ) и ПНС ( б ) при l равном 5 µm
б
-
Fig. 5. Comparison of the distributions of equivalent stresses in the mode I and mode II at plane strain ( a ) and plane stress ( б ) at l equal to 5 µm
Таблица 3
Сингулярность в вершине трещины
Table 3
Crack tip singularity
|
Параметр |
Plane strain |
|||||
|
Mode I |
Mode II |
|||||
|
l = 1 µ m |
l = 5 µ m |
l = 10 µ m |
l = 1 µ m |
l = 5 µ m |
l = 10 µ m |
|
|
Сталь P2M |
–0,647 |
–0,669 |
–0,648 |
–0,562 |
–0,548 |
–0,526 |
|
Сталь 34X |
–0,659 |
–0,672 |
–0,660 |
–0,557 |
–0,530 |
–0,518 |
|
Al-alloy 7050 |
–0,662 |
–0,664 |
–0,654 |
–0,542 |
–0,513 |
–0,505 |
|
Ti-6Al-4V |
–0,649 |
–0,656 |
–0,649 |
–0,539 |
–0,516 |
–0,500 |
|
Параметр |
Plane stress |
|||||
|
Mode I |
Mode II |
|||||
|
l = 1 µ m |
l = 5 µ m |
l = 10 µ m |
l = 1 µ m |
l = 5 µ m |
l = 10 µ m |
|
|
Сталь P2M |
–0,671 |
–0,674 |
–0,662 |
–0,534 |
–0,516 |
–0,515 |
|
Сталь 34X |
–0,680 |
–0,676 |
–0,653 |
–0,531 |
–0,501 |
–0,494 |
|
Al-alloy 7050 |
–0,671 |
–0,639 |
–0,612 |
–0,509 |
–0,486 |
–0,505 |
|
Ti-6Al-4V |
–0,672 |
–0,634 |
–0,611 |
–0,513 |
–0,484 |
–0,486 |
На рис. 6 показаны изменения формы и размера угловых распределений безразмерных эквивалентных напряжений S e для стали Р2М и титанового сплава Ti-6Al-4V в условиях нормального отрыва I и чистого сдвига II как для плоского напряженного состояния, так и для плоской деформации в широком диапазоне значений расстояния до вершины трещины r / l , при фиксированном значении параметра внутренней длины l = 5 µm. Угловые распределения безразмерных напряжений демонстрируют значительную чувствительность к пластическим свойствам материала и заметные различия в поведении Se в зависимости от выбранных соотношений расстояний r / l : 0,018; 0,04; 0,12 и 3,72. Более того, установленная зависимость угловых распределений от радиальной координаты одинаково значима в условиях плоской деформации и плоского напряженного состояния для режимов разрушения I и II, в отличие от обычного классического случая пластичности HRR (Shlyan-nikov et al. 2021 [14]).
Сравнение безразмерных угловых распределений эквивалентных напряжений, показанных на рис. 6, для различных значений нормированных расстояний r / l подтверждает, что поля пластичности градиента деформации, полученные в результате проведенного параметрического исследования, не имеют отдельной формы (Shi et al., 2001 [21]), т. е.
σ iCjMSG ( r ,θ ) ≠ rA λ σˆ ij ( θ ) , (14)
где ( r , θ ) – полярные координаты с центром в вершине трещины, λ – степень сингулярности напряжений, σ i j – тензор напряжений, σˆ ij ( θ ) – соответствующая угловая функция и A – коэффициент амплитуды в зависимости от приложенной нагрузки, конфигурации тела с трещиной и свойств материала. Аналогичные результаты зависимостей полярных распределений безразмерных напряжений наблюдались в наших расчетах для других значений параметра внутренней длины материала, а именно: l = 1 и 10 µm.
Сталь Р2М
Сплав Ti-6Al-4V

Рис. 6. Угловые распределения нормализованных эквивалентных напряжений при ПД и ПНС для режимов разрушения I и II
Fig. 6. Angular distributions of normalized equivalent stresses at plane strain and plane stress for modes I and II
4. Параметры сопротивления разрушению
Одним из основных элементов структуры в анализе полей напряжений, деформаций и перемещений в области вершине трещины являются масштабные коэффициенты в виде коэффициентов амплитуды или коэффициентов интенсивности напряжений (SIF). Эти коэффициенты имеют физическое значение параметров сопротивления разрушению материала и, как правило, зависят от приложенной нагрузки, конфигурации растрескавшегося тела и свойств материала. В литературе имеются ограниченные исследования параметров сопротивления разрушению для теорий градиентной пластичности, и эти исследования ограничены несколькими частными случаями и не имеют достаточного обобщения. Недавно Shlyannikov et al. [14] представили численные и аналитические формулировки для пластических SIF, которые являются параметрами сопротивления разрушению и применимы в области обоснованности градиентной пластичности CMSG теории.
Из результатов Shlyannikov et al. [14, 31] мы принимаем следующую численную формулировку для ампли- туды ApFEM (r,0) и пластический коэффициент интенсивности KPFEM для CMSG-теории, которые задаются:
FEM FEM FEM
ap (г, 0) = аj (г, S)jGj (r, 6); (15)
FEM FEM /—r
KP = AP rr ' , (16)
где r = r// является безразмерным расстоянием до вершины трещины, а у - тип сингулярности напряжений. В уравнении (15) угловые распределения компо-FEM нента напряжения су (r,0) нормализуются через
FEM FEM
O j = O j O Y . Определяющие законы для модели CMSG являются одними из простейших обобщений теории пластичности потока J2, которые включают эффекты градиента деформации.
Расчет пластического SIF KP FEM показывает почти одинаковую величину в зоне с преобладанием градиента перед вершиной трещины. Следовательно, мы берем сходящееся значение и строим его радиальные распределения на рис. 7 для режимов разрушения I и II при плоском напряженном состоянии и плоской деформа-
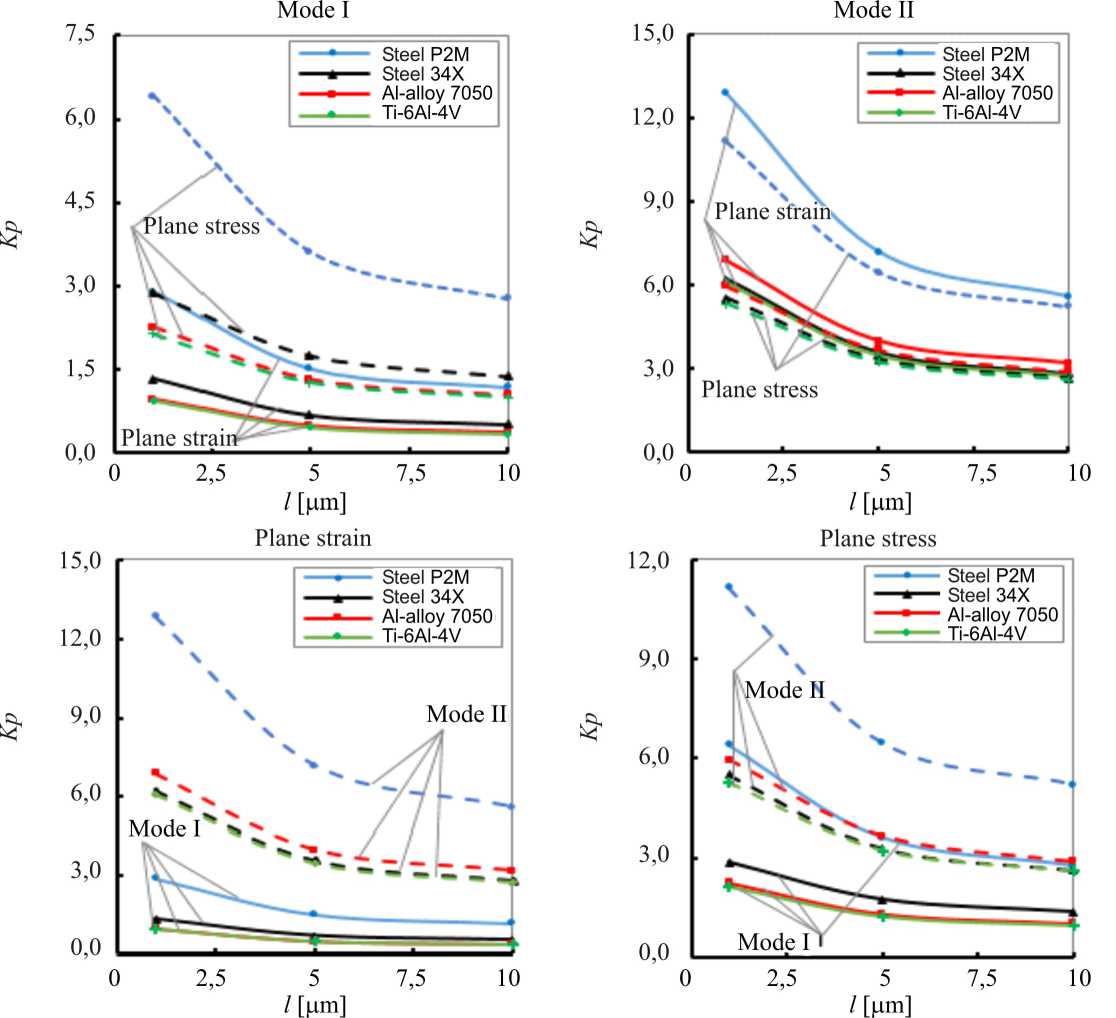
Рис. 7. Поведение пластических коэффициентов интенсивности напряжений как функция параметра характерной длины материала при ПД и ПНС для различных режимов разрушения
Fig. 7. The behavior of plastic stress intensity factors as a function of the parameter of the intrinsic material length at plane strain and plane stress for various fracture modes
ции для различных значений внутренней длины материала l и упругопластических свойств материала. Результаты показывают чувствительность используемого параметра сопротивления разрушению при оценке сопряженных эффектов параметров l и пластических свойств материла. При увеличении параметра длины материала с 1 до 10 µm наблюдается монотонное уменьшение пластических коэффициентов интенсивности напряжений. Меньшие значения пластического SIF, полученные с увеличением l , являются следствием большего влияния градиентов пластической деформации, которые увеличивают сопротивление пластическому потоку. Независимо от величины шкалы длины пластичности CMSG, для случая режима II можно наблюдать более высокий уровень пластичности SIF по сравнению с условиями режима разрушения I.
Важный вывод, касающийся численных результатов, изображенных на рис. 7, по отношению к классическим упругим коэффициентам интенсивности напряжений: новые пластические SIF для CMSG теории отличаются для плоской деформации и плоского напряженного состояния, а также проявляют свойство чувствительности к пластическим свойствам материала и масштабному эффекту внутренней длины, что является важным и привлекательным с точки зрения практического применения.
Заключение
-
1. Результаты исследования показали, что с учетом влияния градиента пластических деформаций и характерной внутренней длины материла истинные локальные напряжения в вершине трещины на порядок и бо- лее выше, чем при классической пластичности в виде HRR-решения. Также для каждого рассмотренного материала при режиме разрушения I распределение полей нормированных эквивалентных напряжений выше при плоском напряженном состоянии, чем при плоской деформации. В то же время различия для режима разрушения II в эквивалентных напряжениях при плоском напряженном состоянии и плоской деформации незначительны. Также выявлено, что вблизи вершины трещины при форме разрушения II происходит эффект разряжения эквивалентных напряжений, когда как по мере удаления от вершины трещины эквивалентные напряжения для режима разрушения II выше, чем при режиме I.
Список литературы Анализ полей напряжений в вершине трещины и параметры сопротивления разрушению в условиях градиентной пластичности
- Nix W.D., Gao H. Indentation size effects in crystalline materials: a law for strain gradient plasticity //j. Mech. Phys. Solids. - 1998. - Vol. 46. - Р. 411-425. doi: 10.1016/S0022-5096(97)00086-0.
- Mechanism-based strain gradient plasticity-I / H. Gao, Y. Huang, W.D. Nix, J.W. Hutchinson // Theory. J. Mech. Phys. Solids. - 1999. - Vol. 47. - Р. 1239-1263.
- Fleck N.A., Hutchinson J.W. A phenomenological theory for strain-gradient effects in plasticity //j. Mech. Phys. Solids. - 1993. - Vol. 41. - Р. 1825-1857.
- Fleck N.A., Hutchinson J.W. Strain gradient plasticity // Adv. Appl. Mech. - 1997. - Vol. 33. - Р. 295-361.
- Fleck N.A., Hutchinson J.W. A reformulation of strain gradient plasticity // J Mech Phys Solids. - 2001. - Vol. 49. - Р. 2245-2271. doi: 10.1016/S0022-5096 (01) 00049-7.
- A conventional theory of mechanism-based strain gradient plasticity / Y. Huang, S. Qu, K.C. Hwang, M. Li, H. Gao // Int. J. Plast. - 2004. - Vol. 20. - Р. 753-782.
- Taylor G.I. Plastic strain in metals //j. Inst. Metals. - 1938. - Vol. 62. - Р. 307-324.
- Strain gradient plasticity: theory and experiment / N.A. Fleck, G.M. Muller, M.F. Ashby, J.W. Hutchinson // Acta Metal. Mater. - 1994. - Vol. 42. - Р. 457-487.
- Gao H., Huang Y. Geometrically necessary dislocation and size-dependent plasticity // Scripta Materialia. - 2003. - Vol. 48. - Р. 113-118.
- Martínez-Pañeda E., Natarajan S., Bordas S. Gradient plasticity crack tip characterization by means of the extended nite element method // Comp. Mech. - 2017. - Vol. 59. - Р. 831-842. doi: 10.1007/s00466-017-1375-6.
- Martínez-Pañeda E., Betegon C. Modeling damage and fracture within strain-gradient plasticity // Int. J. Solids Struct. - 2015. - Vol. 59. - Р. 208-215. doi: 10.1016/j.ijsolstr.2015.02.010.
- Martínez-Pañeda E., Niordson C.F. On fracture in finite strain gradient plasticity // Int. J. Plast. - 2016. - Vol. 80. - Р. 154-167. doi: 10.1016/j.ijplas.2015.09.009.
- Martínez-Pañeda E., Fleck N.A. Mode I crack tip fields: Strain gradient plasticity theory versus J2 flow theory // Europ. J. Mech./A Solids. - 2019. - Vol. 75. - Р. 381-388. doi: 10.1016/j.euromechsol.2019.02.009.
- Crack tip fields and fracture resistance parameters based on strain gradient plasticity / V. Shlyannikov, E. Martínez-Pañeda, A. Tumanov, A. Tartygasheva // Int. J. Solids Struct. - 2021. - Vol. 208-209. - Р. 63-82. doi: 10.1016/j.ijsolstr.2020.10.015.
- Shlyannikov V., Tumanov A., Khamidullin R. Strain-gradient effect on the crack tip dislocations density // Frattura ed Integrità Strutturale. - 2020. - Vol. 54. - P. 205-214. DOI: 10.3221./IGF-ESIS.54.14.
- Шлянников В.Н., Туманов А.В., Хамидуллин Р.М. Эффекты градиентной пластичности в вершине трещины при плоском напряженном состоянии и плоской деформации // Физическая мезомеханика. - 2021. - Р. 257-268. doi: 10.1134/S1029959921030048.
- Shlyannikov V., Fedotova D. Distinctive features of crack growth rate for assumed pure mode II conditions // Int. J. Fatigue. - 2021. - Vol. 147. - Р. 106163. doi: 10.1016/j.ijfatigue.2021.106163.
- Xia Z.C, Hutchinson J.W. Crack tip fields in strain gradient plasticity //j. Mech. Phys. Solids. - 1996. - Vol. 44. - Р. 1621-1648.
- Fracture in mechanism-based strain gradient plasticity / H. Jiang, Y. Huang, Z. Zhuang, K.C. Hwang //j. Mech. Phys. Solids. - 2001. - Vol. 49. - Р. 979-993. doi: 10.1016/S0022-5096 (00) 00070-3.
- The boundary-layer effect on the crack tip field in mechanism-based strain gradient plasticity / M. Shi, Y. Huang, H. Jiang, K.C. Hwang, M. Li // Int. J. Fract. - 2001. - Vol. 112. - Р. 23-41.
- Non-existence of separable crack tip field in mechanism-based strain gradient plasticity / M. Shi, Y. Huang, H. Gao, K.C. Hwang // Int. J. Solids Struct. - 2000. - Vol. 37. - Р. 5995-6010.
- Stölken J.S., Evans A.G. A microbend test method for measuring the plasticity length scale // Acta Mater. - 1998. - Vol. 46. - Р. 5109-5115.
- Individual strain gradient effect on torsional strength of electropolished microscale copper wires / S. Guo, Y. He, J. Lei, Z. Li, D. Liu // Scr. Mater. - 2017. - Vol. 130. - Р. 124-127. doi: 10.1016/j.scriptamat.2016.11.029.
- Mu Y., Hutchinson J.W., Meng W.J. Micro-pillar measurements of plasticity in confined Cu thin films. Extreme Mech. Lett. - 2014. - Vol. 1. - Р. 62-69. doi: 10.1016/j.elm.2014.12.001.
- ANSYS Mechanical APDL Theory Reference Release 14.5 // ANSYS. Inc. Southpointe. 275 Technology Drive, CanonBurg. PA. - 2012.
- Fracture analysis in the conventional theory of mechanism-based strain gradient (CMSG) plasticity / S. Qu, Y. Huang, H. Jiang, C. Liu // Int. J. Fract. - 2004. - Р. 199-220. doi: 10.1023/B: FRAC.0000047786.40200.f8.
- Mikkelsen L.P., Goutianos S. Suppressed plastic deformation at blunt crack-tips due to strain gradient effects // Int. J. Solids Struct. - 2009. - Vol. 46. - Р. 4430-4436. doi: 10.1016/j.ijsolstr.2009.09.001.
- Toward a further understanding of size effects in the torsion of thin metal wires: an experimental and theoretical assessment / D. Liu, Y. He, D.J. Dunstan, B. Zhang, Z. Gan, P. Hu, H. Ding // Int. J. Plast. - 2013. - Vol. 41. - Р. 30-52.
- Mixed mode near-tip fields for cracks in materials with strain gradient effects / Y. Huang, L. Zhang, T.F. Guo, K.C. Hwang //j. Mech. Phys. Solids. - 1997. - Vol. 45. - Р. 439-465.
- Microstructurally sensitive crack nucleation around inclusions in powder metallurgy nickel-based superalloys /j. Jiang, J. Yang, T. Zhang, J. Zou, Y. Wang, F.P.E. Dunne, T.B. Britton // Acta Mater. - 2016. - Vol. 117. - Р. 333-344. DOI: 10/1016/j.actamat.2016.07.023.
- Захаров А.П., Шлянников В.Н., Иштыряков И.С. Пластический коэффициент интенсивности напряжений в задачах механики разрушения // Вестник Пермского национального исследовательского политехнического университета. Механика. - 2019. - № 2. - С. 100-115. doi: 10.15593/perm.mech/2019.2.08.


