Анализ поведения функций, заданных с точностью до интервала

Современная наука и практика обработки информации успешно справляется с задачами исследования различных систем с полностью определёнными (детерминированными) параметрами. Эти задачи обычно формулируются как задачи расчёта, анализа и синтеза тех или иных функций с детерминированными параметрами, служащих соответствующими характеристиками изучаемых систем. Но на практике часто встречаются другие системы - системы с неточно известными, т.е. неполностью определёнными (недетерминированными) параметрами. Причины появления таких систем заключаются в естественной неопределённости, свойственной многим реальным процессам, происходящим в системах; в неточном задании параметров большинства систем из - за неизбежных погрешностей при их вычислении или измерении; в изменении во времени параметров систем; в необходимости или целесообразности совместного исследования целых семейств однотипных систем, имеющих одинаковые функции - харак теристики и различающиеся лишь значениями параметров этих функций. Учёт неопределённости систем особенно важен при их проектировании, поскольку полная определённость в работе системы появляется лишь на последних этапах её создания.

Исследование введённых неопределённых систем формулируется в виде задач расчёта, анализа и синтеза различных функций с недетерминированными параметрами, служащих соответствующими характеристиками данных систем. Все эти задачи значительно сложнее их вышеупомянутых детерминированных аналогов, которые приходится решать при исследовании систем с детерминированными параметрами. Усложнение связано с тем, что алгебра недетерминированных чисел сложнее алгебры детерминированных чисел.

В настоящей статье рассматриваются задачи расчёта и анализа неточно заданных (недетерминированных) функций интервального типа. В качестве математического аппарата используется интервальная алгебра и интервально - дифференциальное исчисление.

1    Постановка задачи

Рассмотрим обычную (детерминированную) функцию одной независимой переменной

• (1)                                       y = f ⁽ x ),

однозначно отображающую заданное множество X = { х } независимых переменных х в заданное множество Y = { у } зависимых переменных у в соответствии с некоторым законом f , который и называется функцией. Хорошо известно, что задача расчёта (вычисления значений) функции (1) решается с помощью адекватного этой задаче математического аппарата алгебры вещественных чисел, при использовании подходящих методов вычисления, а задача анализа поведения функции (1) - с помощью адекватного ей аппарата классического дифференциального исчисления [1].

Рассмотрим теперь недетерминированную (конкретно, интервальную) функцию одной независимой переменной [2]

• (2)                                      y = f ( х ),

однозначно отображающую заданное множество X = { х} независимых вещественных (как и в (1)) переменных х в заданное множество ~ = {~} зависимых переменных - интервалов ~ = [ у , , у ₂ ] , в соответствии с законом ~ , который и называется интервальной функцией. По определению (2), любую интервальную функцию ~ f можно представить в виде пары обычных функций f 1 , f ₂

• (3)                                       f = { f„ f 2 } ,

которые имеют вид

• ⁽⁴⁾                               У 1 = ^f . ( ^х ) у 2= ^f 2^{( х} ).

Из соотношений (3), (4) видно, что интервальная функция f эквивалентна паре обычных функций f 1 , f ₂ , из которых первая однозначно отображает заданное множество X = { х } независимых переменных х функции f в множество Y = { у , } нижних границ интервалов ~ = [ у , , у ₂] - зависимых переменных этой функции, а вторая однозначно отображает то же множество X = { х } в множество Y ₂ = { у ₂} верхних границ интервалов ~ = [ у , , у ₂] - зависимых переменных функции.

Задача настоящей работы заключается в построении двух систематических процедур (алгоритмов), связанных с изучением интервальных функций вида (2). А именно:

■    процедуры расчёта (вычисления значений) интервальной функции; ■    процедуры анализа поведения интервальной функции. 2    Решение задачи вычисления интервальной функции

Начнём с решения задачи расчёта (вычисления значений) интервальной функции. Здесь возможны два случая.

Случай 1 . Интервальная функция задана в разделённом виде, в котором верхняя и нижняя границы интервального значения функции выражены каждая по отдельности. Этот вид представления интервальной функции вытекает из соотношений (2)–(4). Именно, из (2), (3) следует явное представление интервальной функции в виде интервала

• (5)    [ У 1 , у 2] = [ f , ( x ), f _Z( x )] ,

границы которого согласно (5) выражаются формулами

У 1= f | ^{( x} ),   у 2= f 2 ^{( x}).

Итак, вычисление интервального значения ~ = [ у ₁, у ₂] интервальной функции (2), соответствующего значению x независимой переменной этой функции, осуществляется по алгоритму:

Шаг 1. Записываем вычисляемую интервальную функцию (2) в разделенном виде (5), (6) с помощью нижней f 1 и верхней f ₂ граничных функций функции (2).

Шаг 2. Вычисляем нижнюю граничную функцию f 1 , используя для этого какой - либо подходящий известный метод вычисления обычных (детерминированных) функций [3].

Шаг 3. Вычисляем соответствующую верхнюю граничную функцию f ₂ , используя ту же методику, что и на шаге 2.

Шаг 4. Соединяя вычисленные значения нижней f 1 и верхней f ₂ граничных функций, получим явное представление (5) вычисленной интервальной функции (2) в виде интервала.

Случай 2 . Интервальная функция задана в неразделённом виде, т.е. в виде суперпозиции элементарных интервальных функций: интервального сложения и вычитания, умножения интервала на вещественное число, умножения и деления интервалов [4]. В этом случае перед собственно вычислением интервальная функция приводится к разделённому виду, после чего к функции применяется алгоритм случая 1. Приведение любой интервальной функции к разделённому виду можно осуществить с помощью основных формул интервальной математики, выражающих результаты элементарных преобразований интервалов [4]:

^[ a^ a 2^] + ^[ b i , b 2^] = ^{[ a} i +b i , a 2 + b 2 ^]; ^{[ a} 1 , ^a 2 ^]-^{[ b} 1 , ^b 2^{] = [ a}1 -^b 2 , ^a 2 “ ^b 1 ^];

k ^[ a l , a ₂] = Л ka ¹, ka²], ^k >° ^[ a l , a 2 ^]-^[ b l , b 2 ^] = ^[min⁽ a i -b) ^),max⁽ a -b) ^)];

[ ka 2 , ^ка 1 ], k и;                              i , j              i , j

[ a 1 , a 2 ]/[ ) 1 , ) 2] = [ a 1 , a 2Н1/ b ₂,1/ b j

Пример . Привести в области x > 0 к разделённому виду интервальную функцию ~ = ([2,3] x + [1,2] x ) • ([5,7] x + [4,6] x ) .

Решение. Применяя к заданной интервальной функции последовательно третью, первую и четвёртую формулы (7), получим нужный вид функции

~ = [ у ₁, у ₂ ] = ([2 x ,3 x ] + [ x ,2 x ]) • ([5 x ,7 x ] + [4 x ,6 x ]) = [3 x ,5 x ] • [9 x ,13 x ] = [min(3-9 x ²,3 13 x ²,5-9 x ²,5-13 x ²), max(3-9 x ²,3-13 x ²,5-9 x ², 5 13 x ²) = [27 x ²,65 x ²].

Таким образом, у ₁ =27 x ², у ₂ =65 x ², и , наконец, разделённая форма заданной интервальной функции ~ = [ у 1 , у 2 ] = [27 x ²,65 x ²] .

3 Решение задачи анализа поведения интервальной функции: сравнение интервалов

Перейдём к описанию уже упомянутой ранее ( раздел 1) задачи анализа поведения интервальной функции. Постановка этой задачи аналогична постановке задачи анализа поведения обычной детерминированной функции и включает, в первую очередь, отыскание :

• 1)    интервалов возрастания функции;

• 2)    интервалов убывания функции;

• 3)    интервалов постоянства значений функции;

• 4)    точек максимума функции;

• 5)    точек минимума функции.

Кроме того, постановка задачи анализа поведения интервальной функции может включать отыскание особых интервалов (особых точек) такой функции. Существование таких интервалов (таких точек) связано с интервальным характером этой функции. У обычных детерминированных функций такие интервалы (точки) отсутствуют.

Очевидно, что решение задач анализа поведения интервальной функции требует сравнения величин интервалов. В связи с этим ниже кратко изложены основные результаты теории сравнения интервалов [5, 6]. Данные результаты составляют теоретическую базу детермини-зационного подхода к принятию решений в условиях интервальной неопределённости. Теоретические основы других возможных подходов к принятию решений в условиях неопределённости можно найти в литературе [7–10]. Принятие решений в условиях неопределённости является важной составной частью онтологии проектирования [11].

Рассмотрим два интервала ~ = [ a 1 , а ₂] и b = [ b 1, b₂ ] . Попытаемся сравнить величины этих интервалов, рассматривая их как интервальные числа. Прямое сравнение интервалов a ~ и b на основе отношений отдельных пар вещественных чисел ( a i , b j ) , где a i ea, b j ^b , не всегда возможно . Действительно, в общем случае одни пары чисел будут находиться в отношении ( a i >bj ), а другие - в противоположном отношении ( a i < bj ) . Поэтому остаётся только реализовать сравнение интервалов на теоретико - множественном уровне, рассматривая каждый из интервалов как единое целое, неделимое на части. При этом операции нахождения максимума v и минимума л двух интервалов ~=[ a 1 , a ₂] и b = [ b 1 ,b ₂] можно ввести в виде следующих теоретико - множественных конструкций а               b b               ~

• (8)                a v b = \avb | a e a , b e b }, a л Ь = { a A b | a e a , b e b } .

Таким образом, взятие максимума (минимума) двух интервалов ~ и b определяется, согласно (8), как нахождение множества максимумов (минимумов) двух точных величин a и b , при условии, что эти величины пробегают все возможные значения соответственно из интервалов a a и b . Теперь для того, чтобы интервалы a a и b можно было сравнить по величине, при этом установив их отношение а >Ь или ~ <  b , нужно, чтобы :

• 1)    введённые операции v,a над этими интервалами существовали;

• 2)    эти операции давали в результате один из операндов: ~ или b ;

• 3)    указанные две операции были согласованы, т.е. если большим (меньшим) оказывается один из интервалов, то меньшим (большим) является другой из них.

Сформулированное условие сравнимости величин интервалов является, очевидно , необходимым и достаточным.

Нетрудно доказать, что условие согласованности операций v и л над интервалами всегда выполняется. Очевидно также, что эти операции существуют для любой пары а, b , причём результатом операции в общем случае оказывается некоторый новый интервал, отличный как от ~ , так и от b . Таким образом, необходимым и достаточным условием сравнимости интервалов ~ и b оказывается условие, по которому операции а ab и ~ a b должны иметь своим результатом один из интервалов - b или b . Из этой формулировки условия сравнимости интервалов выводятся различные его конструктивные формы, удобные для практического применения. Эти формы содержатся в нижеследующих теоремах 1 - 4.

Теорема 1. Для того чтобы два интервала ~ = [ а₁ , а ₂] и b = [ b₁ , b ₂] были сравнимы по величине и находились в отношении ~ >Ь , необходимо и достаточно выполнения условий

• (9)                                 a i >b_x, а 2 > b 2 ,

а для того чтобы эти интервалы были сравнимы по величине и находились в отношении ~ <  b , необходимо и достаточно выполнения условий

• (10)                               а₁<Ь₁, а ₂< b ₂.

Из этой теоремы вытекает, что любые интервалы ~, b сравнимы по величине (по отношению > или <) и находятся в этом отношении только тогда, когда в таком же отношении находятся их одноименные границы а₁, b₁ и а ₂, b ₂.

Значение теоремы 1 в том, что она сводит сравнение интервалов и выбор большего (меньшего) из них к очевидной операции сравнения границ указанных интервалов, являющихся вещественными числами.

Теорема 2. Для того чтобы два интервала ~ = [ а₁ , а ₂] и b =[ b ₁, b ₂] были несравнимы по величине (по отношению > или <), т.е. не находились в отношении ~ >  b или ~ <  b , необходимо и достаточно выполнения условий

• (11)                      ( а₁₁, а₂>Ь₂) или (b₁<а₁, b₂ >а₂).

Интервалы ~ и b несравнимы по отношениям > и < только тогда, когда один из них полностью «накрывает» другой. Смысл теоремы 2 в том, что она выявляет существование случаев несравнимости интервалов по отношениям > и <, в отличие от обычных вещественных чисел, которые всегда сравнимы по этим отношениям. Несравнимость некоторых интервалов - естественный результат того, что интервальные числа, в отличие от обычных вещественных чисел, задаются не точно, а с неопределённостью (число принимает некоторое значение в заданном интервале, но при этом не уточняется, какое именно это значение).

Будем рассматривать теперь систему нескольких интервалов

• ^{(12)                            а} ₁ ^{=[ а} п, ^а ₁₂ ^] , ^а ₂ ^{=[ а} ₂₁ , ^а ₂₂ ^] , ^а з ^{=[ а} ₃₁ , ^а ₃₂L ...

Сравнение по отношениям >,< величин интервалов выписанной системы (12), рассматриваемых как интервальные числа, реализуется в результате попарного сравнения указанных интервалов, выполняемого в соответствии с теоремами 1 и 2. Главные результаты, получаемые этим путём, содержатся в нижеследующих теоремах 3 и 4.

Теорема 3. Для того чтобы в системе нескольких интервалов (12) существовал максимальный интервал, который находится со всеми остальными интервалами в отношении , и этим интервалом являлся ~₁ , необходимо и достаточно, чтобы границы этого интервала были расположены относительно одноимённых границ всех остальных интервалов согласно условиям

(13)                      {

• ^а 11 -^а 21 , ^а 11 -^а 31 , ^а 11 -^а 41 ,...

• ^а 12 —^а 22 , ^а 12 — ^а 32 , ^а 12 — ^а 42 ^,"•

Теорема 4. Для того чтобы в системе нескольких интервалов (12) существовал минимальный интервал, который находится со всеми остальными интервалами в отношении , и этим интервалом являлся а ~ 1 , необходимо и достаточно, чтобы границы данного интервала были расположены относительно одноимённых границ всех остальных интервалов согласно условиям

{ a il -a 21 , a ll -a 31 , a ll -a 41 ,-'- a 12 -a 22 , a l2 -a 32 , ^а 12 -a 42 ,—

Как показывают теоремы 3 и 4, интервал является максимальным (минимальным) в системе интервалов только тогда, когда максимальны (минимальны) его нижняя граница - среди нижних границ всех интервалов и верхняя граница - среди верхних границ всех интервалов. Подобно случаю сравнения двух интервалов, сравнение произвольного числа интервалов не выявит экстремального интервала, если интервалы, входящие в систему, попарно несравнимы.

До сих пор мы рассматривали процедуры выделения, вообще говоря, нестрого максимального (нестрого минимального) интервала, основанные на теоретико - множественных операциях (8) вычисления нестрогого максимума (нестрогого минимума) двух интервалов. Аналогично этому вводятся процедуры выделения строго максимального (строго минимального) интервала, т.е. единственного интервала, являющегося максимальным (минимальным).

Будем считать равными по определению совпадающие интервалы, т.е. для произвольных интервалов ~ = [ а ₁, а ₂] и b = [ b ₁, b₂ ] , условие их равенства вводится таким образом: ~

• (15)                               ( а = b ) о ( а ₁ = b ₁, а ₂ = b ₂) .

Из выражения (15) следует, что неравными являются интервалы, удовлетворяющие следующему условию:

• (16)                              (~ bb ) <=> ( а₁ ь^ или а ₂ bb ₂) .

Теперь определение того факта, что некоторый интервал ~ является строго максимальным из двух интервалов ~, b можно записать в виде

• (17)                           (a > b )«(~v b =~, a A b=b , a * b ) ,

аналогичным образом, определение того, что некоторый интервал а ~ является строго минимальным из двух интервалов ~, b записывается в виде

• (18)                            (a < b )о(a bbbb , a л Ь =~, ab b ) .

Здесь v и л - теоретико - множественные операции (8) вычисления максимума и минимума двух интервалов.

Из формулировки условий (17), (18) сравнимости интервалов в виде строгих неравенств между ними можно вывести различные конструктивные формы этих условий, удобные для практики. Такие формы содержатся в теоремах 5–8, которые подобны теоремам 1–4, дающим удобные конструктивные формы сравнимости интервалов в виде нестрогих неравенств.

Теорема 5. Для того чтобы два интервала ~ = [ а ₁, а ₂], b = [ b ₁, b ₂] были сравнимы по величине и находились в отношении ~ >  b , необходимо и достаточно выполнения условий

• (19)                              ( а₁ >b ₁, а ₂ >Ь ₂) или ( а₁ >Ь₁, а ₂ > b ₂),

а для того чтобы эти интервалы были сравнимы по величине и находились в отношении ~ <  b , необходимо и достаточно выполнения условий

• (20)                              ( а₁₁, а₂<b₂) или (а₁<Ь₁, а₂<b₂).

Из теоремы ясно, что интервалы ~ и b сравнимы по величине (по отношению > или <) и находятся в указанном отношении лишь тогда, когда в том же отношении находятся их нижние границы а1, b1 (при этом верхние границы а2, b2 находятся в соответствующем не- строгом отношении: для > это >, а для < это <) или же, наоборот, их верхние границы а2, b2 (при этом нижние границы а1, b1 находятся в соответствующем нестрогом отношении).

Теорема 6. Для того чтобы два интервала ~=[ а 1 , а ₂ ] и b = [ b 1 ,b ₂]были не сравнимы по величине (по отношению > или < ), т.е. не находились в отношении ~ >  b или ~ <  b , необходимо и достаточно выполнения условий

• (21)               ( а 1 1 , а ₂ > b ₂) или (b 1 <  а 1 , b ₂ >  а ₂) или ( а 1 = b 1 , а ₂ = b ₂).

Итак, произвольные интервалы а и b не сравнимы по отношениям > и < только в тех случаях, когда один из них полностью «накрывает» другой либо когда интервалы равны между собой. Значение теоремы 6 в том, что она показывает существование случаев несравнимости интервалов по отношениям > и < даже тогда, когда сравниваемые интервалы не равны между собой, а только «накрывают» один другой. Эта ситуация отличается от ситуации со сравнением вещественных чисел, где неравные числа всегда сравнимы по отношениям > и < .

Рассмотрим теперь систему нескольких интервалов (12). Сравнение по отношениям > и < величин интервалов системы (12), рассматриваемых как интервальные числа, реализуется путем попарного сравнения этих интервалов, в соответствии с теоремами 5 и 6. Основные результаты, получаемые этим путём, изложены в нижеследующих теоремах 7 и 8.

Теорема 7. Для того чтобы в системе нескольких интервалов (12) существовал максимальный интервал, который находится со всеми остальными интервалами в отношении , и этим интервалом был а ~ 1 , необходимо и достаточно, чтобы границы этого интервала были расположены относительно одноимённых границ всех остальных интервалов согласно условиям

(а11 >а21, а12 >а22) или (аи >а21, а12>

(ац > а31, а12 > а32) ИЛИ (ап > а31, а12 > а32)

(аи >а41, а12 >а42) или (ап >а41, а12 >а42)"

Теорема 8. Для того чтобы в системе нескольких интервалов (12) существовал минимальный интервал, который находится со всеми остальными интервалами в отношении < , и этим интервалом являлся а ~ 1 , необходимо и достаточно, чтобы границы данного интервала были расположены относительно одноимённых границ всех остальных интервалов согласно условиям ( а_и<а ₂₁ , а ₁₂< а ₂₂ ) или ( а_н<а ₂₁ , а ₁₂< а ₂₂ )

^{( а}_п< ^а 31 , ^а 12 <^а 32 ) ^{или ( а} 11 < ^а 31 , ^а 12,< ^а 32 ) ,

( а_п<а ₄₁ , а ₁₂< а ₄₂ ) или ( а_п<а ₄₁ , а ₁₂< а ₄₂ ) "

4 Решение задачи анализа поведения интервальной функции.Основные теоремы и алгоритм

В предыдущем разделе изложен вспомогательный для задачи анализа поведения интервальной функции материал, связанный со сравнением интервальных величин. Теперь можно перейти к анализу собственно поведения интервальных функций.

Рассмотрим произвольную интервальную функцию (2). Будем считать, что эта функция задана в разделённом виде (5), (6). Это не ограничивает общности рассмотрения, так как функция, заданная в неразделённом виде, всегда может быть приведена к разделённому виду (см. раздел 2). Будем также полагать, что нижняя и верхняя граничные функции интерваль- ной функции непрерывны и дифференцируемы. Сформулируем условия, при которых функция возрастает, убывает, остается постоянной, достигает максимума (минимума), ведёт себя иным способом.

По аналогии с обычными (детерминированными) функциями [1] введём понятия возрастания, убывания, постоянства, максимума и минимума интервальной функции.

Определение 1. Интервальная функция y = f ( x ) называется возрастающей на интервале ( a , b ) , если для любых x 1 и x ₂ из указанного интервала, для которых x 1 <  x ₂ , выполняется неравенство f ( x 1 ) <  f ( x ₂ ) .

Определение 2. Интервальная функция y = f ( x ) называется убывающей на интервале ( a , b ) , если для любых x 1 и x ₂ из данного интервала, для которых x 1 ₂, выполняется неравенство f (x1) > f (x₂ ).

Определение 3. Интервальная функция y = f ( x ) называется постоянной на интервале ( a , b ) , если для любых x 1 и x ₂ из этого интервала, для которых x 1 ₂ , выполняется равенство f ( x j ) = f ( x 2 ) .

Определение 4. Точка x = x0 называется точкой максимума заданной интервальной функции y = f (x), а само число f (x0) - максимумом этой функции, если для всех точек x из некоторой окрестности точки x0 , не совпадающих с x0 , истинно строгое неравенство ~     ~ f ( x q)> f (x).

Определение 5. Точка x = x ₀ называется точкой минимума интервальной функции y = f ( x ) , а число f ( x ₀) - минимумом этой функции, если для всех точек x из некоторой окрестности точки x ₀ , не совпадающих с x ₀ , выполняется строгое неравенство f ( x ₀ ) <  f ( x ).

Введём теперь понятия расширения и сужения интервальной функции, которые не применимы к обычным (детерминированным) функциям.

Определение 6. Интервальная функция y = f ( x ) называется расширяющейся на интервале ( а , b ) , если для любых точек x 1 и x ₂ из этого интервала, для которых x ₂, интервал f(x₂) полностью «накрывает» интервал f (xj).

Определение 7. Интервальная функция y = f ( x ) называется сужающейся на интервале ( a , b ) , если для любых x и x ₂ из данного интервала, для которых x _t< x ₂ , интервал f ( x j ) полностью «накрывает» интервал f ( x ₂) .

Определение 8. Точку x = x ₀ будем называть точкой максимального расширения интервальной функции y = f ( x ) , а число D ( x ₀) = f ₂( x ₀)- f , ( x ₀) - максимальной шириной указанной функции, если для всех точек x из некоторой окрестности точки x ₀ , не совпадающих с x ₀ , интервал f ( x ₀) полностью «накрывает» интервал f ( x ).

Определение 9. Точку x = x ₀ будем называть точкой максимального сужения интервальной функции y =f ( x ) , а число d ( x ₀ ) = f ₂ ( x ₀ ) - f ₍ ( x ₀ ) - минимальной шириной функции f ( x ), если для всех точек x некоторой окрестности точки x ₀, не совпадающих с x ₀, интервал f ( x ) полностью «накрывает» f ( x ₀ ).

Сформулируем и докажем условия, которые определяют то или иное поведение интервальной функции.

Теорема 9. Для того чтобы интервальная функция у = f ( x ) являлась возрастающей на интервале ( a , b ) , необходимо и достаточно, чтобы на указанном интервале её нижняя граничная функция f 1 ( x ) была возрастающей, а верхняя граничная функция f ₂ ( x ) - неубывающей либо, наоборот, функция f ₂( x ) была возрастающей, а функция f _l( x ) - неубывающей.

Доказательство. Представим интервальную функцию y=f ( x ) в интервальной форме (5): у = [ f _l( x ), f ₂( x )] . Возрастание данной функции на интервале ( а , b ) по определению 1 означает, что для любых x₁, x ₂ из этого интервала, таких, что x₁₂, выполняется неравенство [f_i(x₁), f₂(x₁)] < [f_i(x₂), f₂(x₂)], которое, по теореме 5, приводит к двум возможным вариантам: ^fl⁽x1)<^f,(x2), ^f2⁽xl)^^f2⁽x2) или ^fl⁽xl)^^fl⁽x2), ^f2⁽xi)<^f2⁽x2)'

Итак, либо на всём интервале ( а , b ) нижняя граничная функция f ( x ) интервальной функции y = f ( x ) является возрастающей, а верхняя граничная функция f ₂ ( x ) - неубывающей либо наоборот, f ₂( x ) является возрастающей, f ( x ) - неубывающей, что и требовалось доказать.

Теорема 10. Для того чтобы интервальная функция y = f ( x ) была убывающей на интервале ( а , b ) , необходимо и достаточно, чтобы на указанном интервале её нижняя граничная функция f 1 ( x ) была убывающей, а верхняя граничная функция f 2 ( x ) - невозрастающей либо, наоборот, функция f ₂ ( x ) была убывающей, а функция f _l ( x ) - невозрастающей.

Доказательство аналогично доказательству теоремы 9, однако использует определение 2 вместо определения 1.

Теорема 11. Для того чтобы интервальная функция у = f ( x ) была постоянной на интервале ( а , b ) , необходимо и достаточно, чтобы на этом интервале её нижняя f _l ( x ) и верхняя f ₂( x ) граничные функции были постоянными.

Доказательство следует из определения интервала как множества всех вещественных чисел между заданными двумя числами - границами интервала, включая сами границы.

Теорема 12. Для того чтобы x = x ₀ была точкой максимума интервальной функции у = / ( x ) , а число f ( x ₀) - максимумом этой функции, необходимо и достаточно, чтобы в указанной точке достигала максимума её нижняя граничная функция f 1 ( x ) и не достигала минимума её верхняя граничная функция f ₂ ( x ) либо, наоборот, достигала максимума её верхняя граничная функция f ₂ ( x ) и не достигала минимума её нижняя граничная функция f _l ( x ).

Доказательство. Представим нашу интервальную функцию у = f ( x ) в интервальной форме (5): у = [ f ₍ ( x ), f ₂ ( x )] . Существование максимума этой функции в точке x = x ₀ по определению 4 означает, что для всех точек x из некоторой окрестности точки x ₀ , не совпадающих с x ₀ ,     выполняется неравенство     f ( x ₀)> f ( x )    или, в интервальной форме

[ f _l ( x ₀ ), f ₂ ( x ₀ )]>[ f X x ), f ₂ ( x )] , причём последнее неравенство, согласно теореме 5, эквивалентно условию

^{( f} I ^{( x} 0 ) >  ^f I^{( x} ), ^f 2^{( x} 0 ) ^ ^f 2^{( x} )) ^{или (} f l^{( x} 0 ) ^ ^f l^{( x} X ^f 2 ^{( x} 0 ) >  ^f 2^{( x} )) .

Условия левой скобки показывают, что в точке x ₀ функция f 1 ( x ) обращается в максимум, функция f ₂( x ) при этом не обращается в минимум. Условия правой скобки говорят, что в точке x ₀ функция f ₂ ( x ) обращается в максимум, а функция f 1 ( x ) не обращается в минимум, что и требовалось доказать.

Теорема 13. Для того чтобы x = x ₀ была точкой минимума интервальной функции y = f ( x ) , а число f ( x ₀ ) - минимумом этой функции, необходимо и достаточно, чтобы в указанной точке достигала минимума её нижняя граничная функция f ( x ) и не достигала максимума её верхняя граничная функция f ₂ ( x ) либо, наоборот, достигала минимума её верхняя граничная функция f ₂ ( x ) и не достигала максимума её нижняя граничная функция f _ ( x ).

Доказательство теоремы 13 аналогично доказательству теоремы 12, но использует определение 5.

Теорема 14. Для того чтобы интервальная функция y = f ( x ) являлась расширяющейся на интервале ( a , b ) , необходимо и достаточно, чтобы на этом интервале была убывающей её нижняя граничная функция f , ( x ) и была возрастающей её верхняя граничная функция f ₂ ( x ).

Доказательство. Для любых x ₁, x ₂ из интервала ( а , b ) , таких, что x < x ₂ , в силу расширения функции f на этом интервале должно выполняться условие: интервал f ( x ₂ ) полностью «накрывает» f ( x 1 ) . Выражая интервалы в интервальной форме f ( x 1 ) = [ f ( x ), f ₂( x 1 )], f ( x ₂) = [ f ( x ₂), f ₂( x ₂)] , имеем условие «накрытия» интервалов:

^f 1 ( ^x 2)< ^f l ⁽ x l ), ^f 2 ^{( x} 2) >  ^f 2 ^{( x} 1 ^{) .}

Первое из неравенств показывает, что функция f 1 ( x ) убывающая, а второе - что функция f ₂ ( x ) возрастающая. Что и требовалось доказать.

Теорема 15. Для того чтобы интервальная функция ~ = ~ ( x ) была сужающейся на интервале ( а , b ) , необходимо и достаточно, чтобы на данном интервале была убывающей её верхняя граничная функция f ₂ ( x ) и была возрастающей её нижняя граничная функция f 1 ( x ).

Доказательство аналогично доказательству теоремы 14.

Теорема 16. Для того чтобы точка x = x ₀ являлась точкой максимального расширения интервальной функции y = ~ ( x ) , а число D ( x ₀)= f ₂( x ₀)- f 1 ( x ₀) максимальной шириной этой функции, необходимо и достаточно, чтобы в некоторой окрестности точки x 0 слева функция y = 7 ( x ) была расширяющейся, а в некоторой окрестности точки x ₀ справа она была сужающейся.

Теорема 17. Для того чтобы точка x = x ₀ была точкой максимального сужения интервальной функции y = f ( x ) , а число d ( x ₀ )= f ₂( x ₀)- f 1 ( x ₀) минимальной шириной данной функции, необходимо и достаточно, чтобы в некоторой окрестности точки x 0 слева функция y = f ( x ) была сужающейся, а в некоторой окрестности точки x ₀ справа она была расширяющейся.

Доказательства теорем 16 и 17 вытекают прямо из определений 8 и 9 точек максимального расширения и сужения интервальной функции.

Анализ поведения интервальной функции y = f (x) , согласно изложенному в этом разделе материалу, всегда сводится к анализу поведения двух обычных детерминированных функций: нижней f1(x) и верхней f2(x) граничных функций функции f (x). Это позволяет использовать для анализа поведения интервальных функций хорошо известные и разработанные методы анализа поведения обычных (детерминированных) функций, основанные на применении классического дифференциального исчисления [1]. При этом алгоритм анализа поведения произвольной интервальной функции может быть описан следующим образом.

Шаг 1. Проверка формы, в которой представлена интервальная функция у = f ( x ) , подлежащая анализу. Если она неразделённая, т.е. не имеющая вид интервала у ⁼ [ У 1 , У ₂] ⁼ [ f X x ), f ₂( x )] , где У 1 ⁼ f X x ) и у ₂ = f ₂( x ) — соответственно нижняя и верхняя граничные функции заданной интервальной функции, то выполняем переход к шагу 2. Если она разделённая, т.е. имеющая указанный вид, то переход к шагу 3.

Шаг 2. Приведение функции у = f ( x ) из неразделённого вида к разделённому с помощью основных формул интервальной математики (7) (см. раздел 2).

Шаг 3. Анализ поведения нижней граничной функции у . = f . ( x ) интервальной функции у = ~ ( x ) с помощью известных методов анализа поведения обычных (детерминированных ) функций, на основе классического дифференциального исчисления. В ходе анализа устанавливаем интервалы возрастания и убывания функции f 1 и точки её максимумов и минимумов.

Шаг 4. Анализ поведения верхней граничной функции у ₂ = f >( x ) интервальной функции выполняется теми же методами и по той же программе, что и предыдущий шаг.

Шаг 5. Составление сводной таблицы поведения граничных функций у = f₁ ( x ), у ₂ = f , ( x ) путём заполнения в ней первых трёх строк (см. таблицу , в соответствии с результатом анализа поведения функций f . ( x ) и f ₂ ( x ) (шаги 3, 4).

Шаг 6. Анализ сводной таблицы с помощью теорем 9-15, позволяющих идентифицировать последовательные интервалы (-со, x . ),( x . , x ₂),...,( x n_ 1 , x n ),( x n ,oo) в ней как интервалы возрастания, убывания, расширения или сужения анализируемой интервальной функции ~ = f ( x ), а промежуточные точки x . , x ₂ ,..., x n между интервалами как точки максимума (минимума) у = f ( x ) или точки максимума (минимума) её расширения или сужения. Например, если на некотором интервале ( x _; , x _{; +1}) функция f ₂ ( x ) возрастает, а на соседнем интервале ( x i ₊₁, x i ₊₂) убывает, так что в точке x i ₊₁ она максимальна, и при этом функция f . ( x ) на обоих интервалах постоянная, то согласно теоремам 9, 10, 12 интервальная функция y = f ( x ) на интервале ( x i , x i ₊₁) возрастает, в точке x i ₊₁ достигает максимума, затем на интервале ( x i ₊₁ , x i ₊₂) убывает.

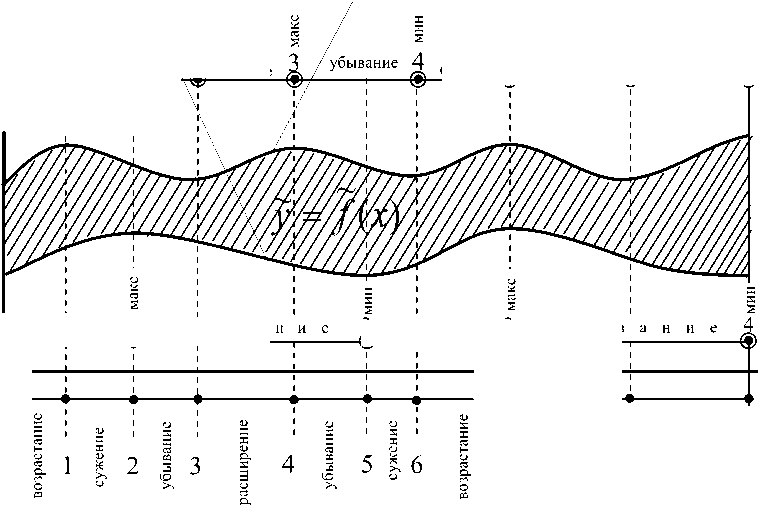
После выполнения шага 6 заполняется четвёртая строка сводной таблицы поведения и на этом анализ поведения заданной интервальной функции заканчивается. Характерный возможный вид четвёртой строки сводной таблицы поведения интервальной функции проиллюстрирован в таблице. По результатам анализа можно вычертить график функции y = f ( x ) ( см. рисунок ).

Заключение

В настоящей статье разработаны систематические методы решения задач расчёта и анализа поведения недетерминированных функций интервального типа, в которых функции определяются с точностью до интервала возможных значений. В качестве математического аппарата использованы интервальная алгебра и дифференциальные характеристики верхней и нижней границ интервальных функций, которые можно рассматривать как специальное дифференциальное исчисление для неточно задаваемых функций интервального типа.

y ₁ f ₁ ( x )

y ₂ f ₂ ( x )

~

y

y ₁

возрастание возрастание

Щ

и cd у cd возрастание

5 убывание 6 возрастание 7

5        \

1 убывание

Поведение функции y2 f2(x)

y ₂

возрастание 1

Поведение функции y ₁ f ₁ ( x )

Поведение функции ~ y  f ( x )

^

убывание    расширение

7          8          9

у

бы

в

а

2 возрастание 3 у б ы в

£

-^- x

Таблица – Сводная таблица поведения граничных функций, определяющих интервальную функцию

y	(    , x 1)	x 1	( x 1, x 2)	x 2	( x 2 , x 3 )	x 3	( x 3 , x 4 )		( xn 1 , xn )	xn	( xn , )
y 1 f 1( x )	о н о	со ^ 5g Я ад 5 Я Я S	Я н	& со ^ 5g Я Я Я ад	cd Н	m ^ ад S § о ад	н		я о н	5g Я ад В Я S S § ад	я н
y 2    f 2 ( x )	Я Я о н о Я о	& СО ^ Я Я	Я н	со ^ 5g я ад В Я Я ад	ад н о S	& m ^ s S со § S	я о н		я н о	& я ад В ад	н
~ y ~ f ( x )	о cd н о cd Он со М	о	о ад	§	о Он	О s & У о ад ад	о		о о	о Я ад 5 о	о Он

Рисунок - Пример интервальной функции

~, y = f (X) (У1 = f1(X) – нижняя граничная функция,

У 2 ⁼ f 2 ( X ) — верхняя граничная функция)