Анализ работы несущих конструкций покрытия большепролетного спортивного сооружения

В связи с проведением в России целого ряда международных соревнований, таких как Универсиада в Казани в 2013 г., Зимние Олимпийские игры в Сочи в 2014 г., Чемпионат мира по футболу в 2018 г. и др. особое внимание уделяется вопросу проектирования и строительства уникальных большепролетных спортивных сооружений. Каждая вновь построенная спортивная арена демонстрирует последние достижения архитектуры, науки и техники, знания и творческий потенциал проектировщиков.

При создании уникального сооружения основным принципом формообразования, в большинстве случаев, является архитектурная идея [1]. Подобные сооружения требуют комплексного подхода и взаимодействия целого ряда специалистов: архитекторов, конструкторов, технологов, строителей. На всех этапах проектирования объекты претерпевают множество изменений в архитектурном и конструктивном плане и, как следствие, требуют постоянного перерасчета. Кроме того, в связи с ужесточившимися в последние десятилетия требованиями к экономичности сооружений, перед проектировщиками встает задача выбора оптимального решения, которая, применительно к уникальному объекту, может быть решена с использованием вариантного проектирования  [2,3].  Для снижения трудоемкости вычислительных работ и сокращения сроков проектирования используют вычислительные комплексы, основанные на численных методах расчета. Одним из основных численных методов для расчета строительных конструкций является метод конечных элементов (МКЭ). Метод имеет обоснованную теоретическую базу. Возможности реализации его в САПР изложены в трудах А. С. Городецкого [4,5], А. В. Перельмутера, В. И. Сливкера [6]. На сегодняшний день на основе МКЭ создано множество универсальных и специализированных вычислительных комплексов одним из наиболее востребованных из которых в России и странах СНГ является "Интегрированная система прочностного анализа и проектирования конструкций Structure CAD Office" (далее ПК SCAD) [7].

Обзор литературы

Исследование конструктивных схем покрытий большепролетных уникальных спортивных сооружений невозможно без использования мирового и отечественного опыта проектирования и строительства подобных объектов.

На сегодняшний день существует множество работ посвященных подобным сооружениям в России и странах СНГ [8-18]. Иностранный опыт по проектированию и анализу работы пространственных покрытий различных сооружений описан в работах [19-32]. Наибольший интерес представляют работы по исследованию покрытий таких объектов, как Большая спортивная арена в Лужниках [8-10], Ледовый дворец спорта на Ходынском поле в г. Москва [11], Большая ледовая арена для хоккея с шайбой в г. Сочи [16], а также зарубежных объектов: футбольный стадион в Браге [19, 20], Олимпийский стадион в Монреале [21], стадионы в Шанхае [22], Пирее [32] и Риме [27].

Значительная часть публикаций посвящена проблемам проектирования, исследованию действительной работы и мониторингу уникальных объектов. В работах приводятся результаты КЭ анализа сооружений. При этом недостаточно внимания уделяется описанию методов построения расчетных моделей, что является актуальной проблемой [33, 34].

Наиболее близки к рассматриваемой тематике работы Назарова Ю. П. [16, 17], расчет покрытия АВК «Внуково-1» [18], а также исследования покрытий стадионов в Браге [19, 20] и Монреале [21]. Некоторые частные случаи оптимизации строительных конструкций освещены в работах зарубежных авторов [35, 36].

Постановка задачи

Цель данной работы — исследовать напряженно-деформированное состояние различных вариантов несущих конструкций покрытия большепролетного сооружения в ПК SCAD, выбрать наиболее рациональное конструктивное решение по показателю материалоемкости.

Из поставленной цели вытекают следующие задачи:

• -    создать КЭ модели пространственной металлической конструкции покрытия ледового дворца “Большой” в ПК SCAD;

• -    провести анализ напряженно-деформированного состояния элементов основной несущей конструкции покрытия;

• -    выбрать и обосновать критерий оптимизации (целевую функцию);

• -    осуществить сравнение исследуемых вариантов модели по выбранному критерию.

Краткая характеристика объекта

Ледовый дворец “Большой” выполнен в смешанном каркасе, состоит из 8 этажного здания с колоннами, перекрытиями, трибунами, лифтовыми и лестничными шахтами, выполняющими роль диафрагм жесткости, запроектированными в монолитном железобетонном каркасе, и металлического покрытия, состоящего из двух частей: покрытия центральной хоккейной площадки и покрытия вестибюльной части.

Покрытие арены (рисунок 1) представляет собой эллипсоид, образованный конструкциями плоских шпренгельных ферм переменного пролета с треугольной решеткой для центральной части и саблевидных ферм с треугольной решёткой в вестибюльной части. Размеры купола в плане 196х144мм, высота – 35м.

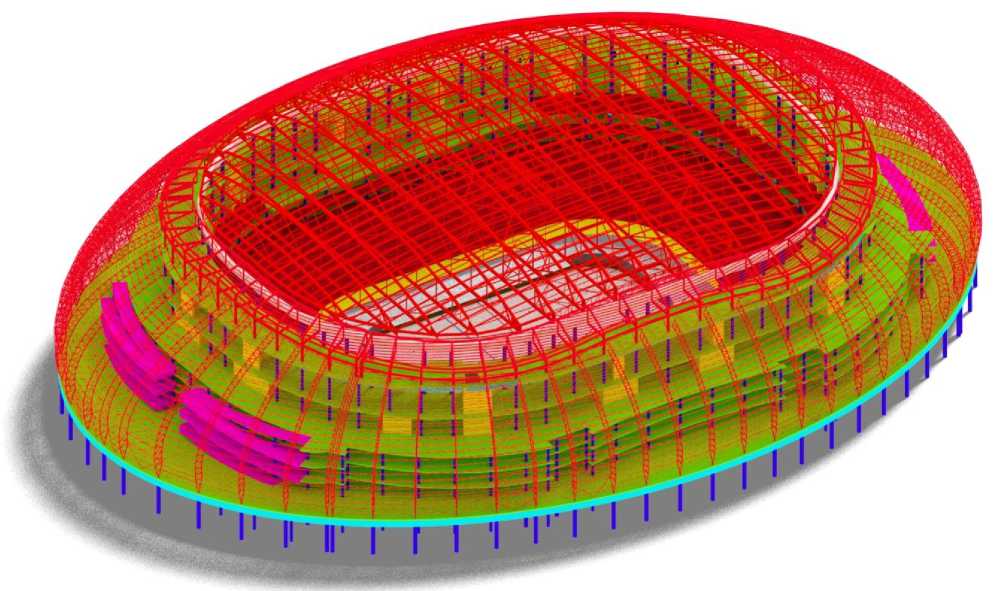
Рисунок 1. Несущий каркас ледового дворца “Большой”

Покрытие центральной хоккейной площадки, состоящее из 18 плоских ферм, 9 типоразмеров с треугольной шпренгельной системой, связанных в пространственную конструкцию опорным кольцом, связями по нижним и верхним поясам, прогонами опирается на железобетонное кольцо. Длина большепролетных ферм от 53,7 до 94,4 м, высота – от 5,5 до 11,74м. Фермы установлены с переменным шагом от 6,5 до 7,5 м.

Верхние и нижние пояса ферм выполнены из сварных двутавров переменного сечения высотой 520 мм и шириной 440мм. Стойки и раскосы выполнены из квадратных и прямоугольных труб. Один конец ферм закреплён шарнирно-неподвижно, а другой линейно-шарнирно-подвижно.

Покрытие вестибюлей и галерей стадиона, образованно 68 стальными фермами - полуарками, длиной от 27,5 до 40 м. Верхний и нижний пояс, треугольная решетка, выполнены из круглой трубы. Нагрузки от кровли передаются на полуарки через систему плоских ферм, расположенных в перпендикулярном направлении к полуаркам на границах панелей ферм. Нижняя часть полуарок опирается на стилобат. Верхняя часть полуарок опирается на перекрытие на отметке +22,100 м, где в совокупности с дополнительными связями образуют диафрагму жесткости. Диафрагма жесткости является связующим звеном между «саблевидными» фермами покрытия вестибюлей и фермами основной части купола.

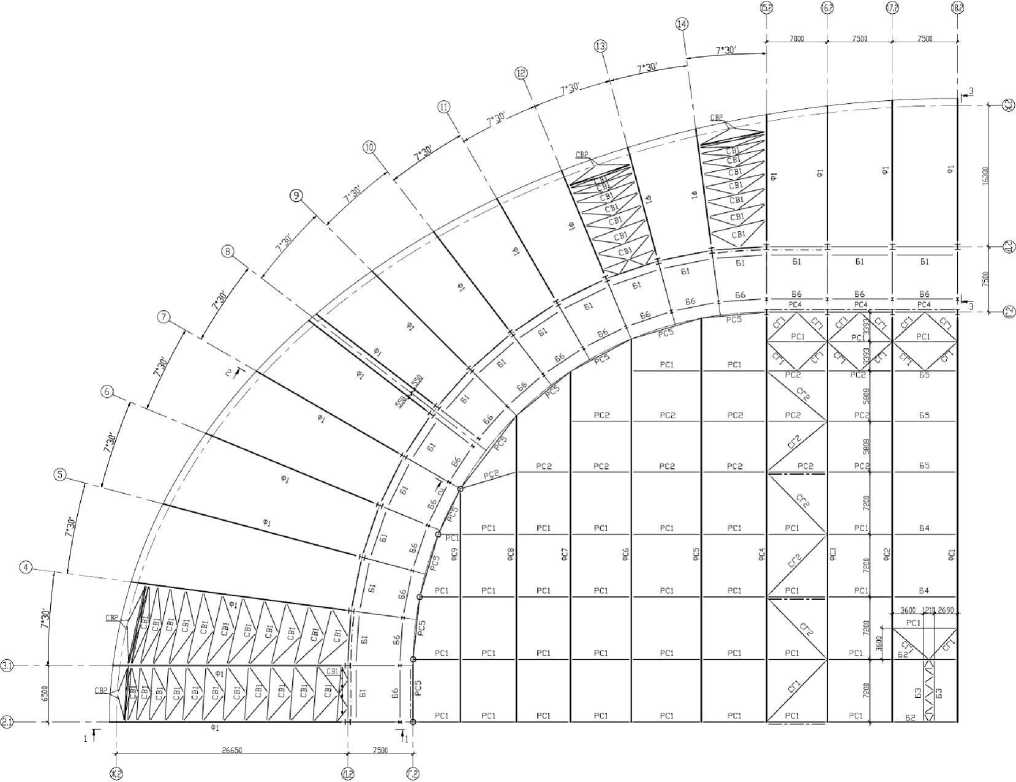
Рисунок 2. Фрагмент схемы расположения несущих конструкций покрытия

Ограждающие конструкции покрытия состоят из: витражной части, выполненной из стеклопакетов и кровли - алюминиевая система «Kalzip». Общая площадь кровли 22,6 тысячи квадратных метров.

Моделирование покрытия в AutoCAD

Для геометрического моделирования несущих конструкций покрытия использовалась программа AutoCAD. На первом этапе смоделирована геометрия семнадцати полуарок. В трехмерном пространстве, используя схему расположения элементов, полуарки четверти покрытия устанавливались в проектное положение (рисунок 3).

Далее смоделированы диафрагма жесткости, на которую в верхней части опираются арки, решетчатые прогоны между арками, а также система продольных и поперечных связей (рисунок 4). В дальнейшем покрытие вестибюлей соединяется с покрытием арены (плоские фермы) (рисунок 5). Моделируются остальные элементы, и, с учетом симметрии, получаем полную расчетную схему (рисунок 6).

Construction of Unique Buildings and Structures, 2015, №4 (31)

Рисунок 3. Саблевидные фермы

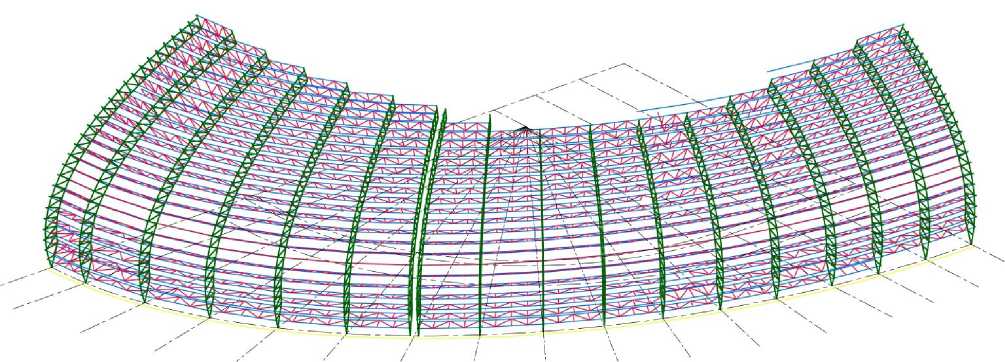
Рисунок 4. Добавление решетчатых прогонов

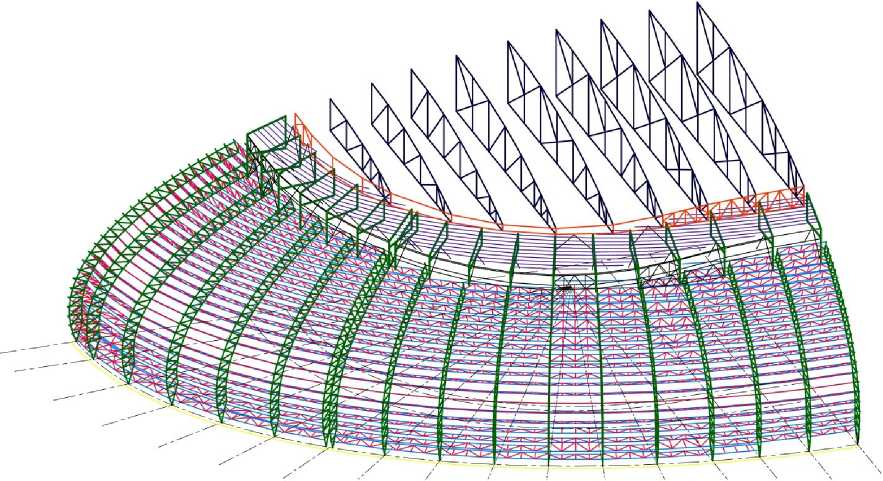
Рисунок 5. Добавление ферм центрального покрытия

Construction of Unique Buildings and Structures, 2015, №4 (31)

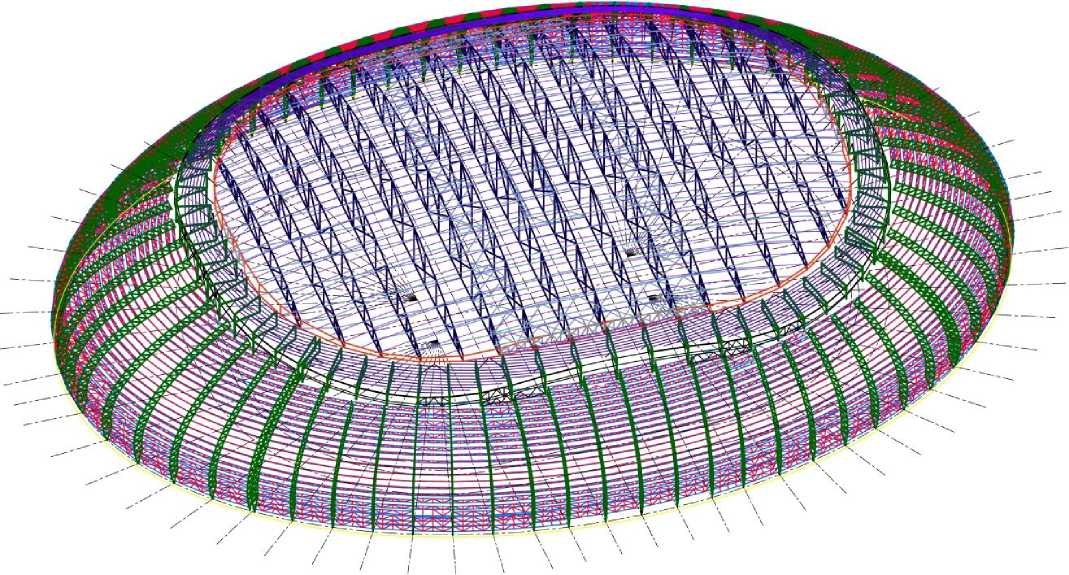
Рисунок 6. Полная расчетная схема в AutoCAD

Создание КЭ модели покрытия в ПК SCAD

Рассматриваемый объект является уникальным сооружением со сложной конструктивной схемой, состоящей из большого числа элементов. Уровень ответственности 1а (коэффициент надежности по ответственности γ_n = 1.2 ). Традиционные способы создания расчетных моделей посредством ввода узлов и элементов будут достаточно трудоемки, а также возрастет вероятность появления субъективных ошибок.

Для устранения этих факторов использованы следующие возможности ПК SCAD [7]:

• -  импорт геометрии системы из программы AutoCAD;

• -  прочтение данных из текстового файла;

• -  режим сборки.

Выделены следующие группы элементов конструкции покрытия: фермы центральной части, полуарки, вспомогательные фермы, ограждающие конструкции. Алгоритм создания расчетной модели приведен на рисунке 7.

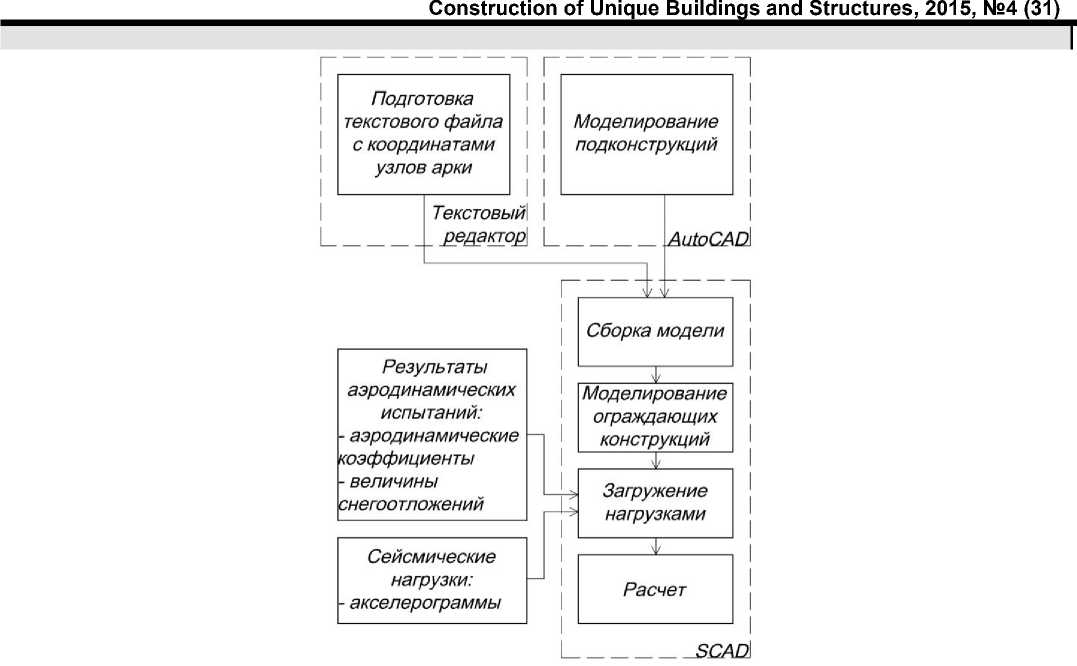
Рисунок 7. Алгоритм создания расчетной модели

В результате получена модель несущих конструкций покрытия в среде ПК SCAD, показанная на рисунке 8.

Рисунок 8. Конечно-элементная модель расчетной схемы в ПК SCAD

Характеристика нагрузок и расчет

На пространственный каркас действуют постоянные нагрузки – от веса ограждающих и несущих конструкций здания, временные – атмосферные (снег и ветер), а также технологические, температурные.

Собственный вес конструкций был задан автоматически при помощи функции задания собственного веса. Технологические нагрузки были приложены на соответствующие узлы и элементы согласно схеме расположения оборудования.

Снеговая нагрузка вычислялась по [1] и результатам аэродинамических исследований, прикладывалась к ограждающим элементам покрытия. Рассматривалось 4 варианта снегового загружения (рисунок 9).

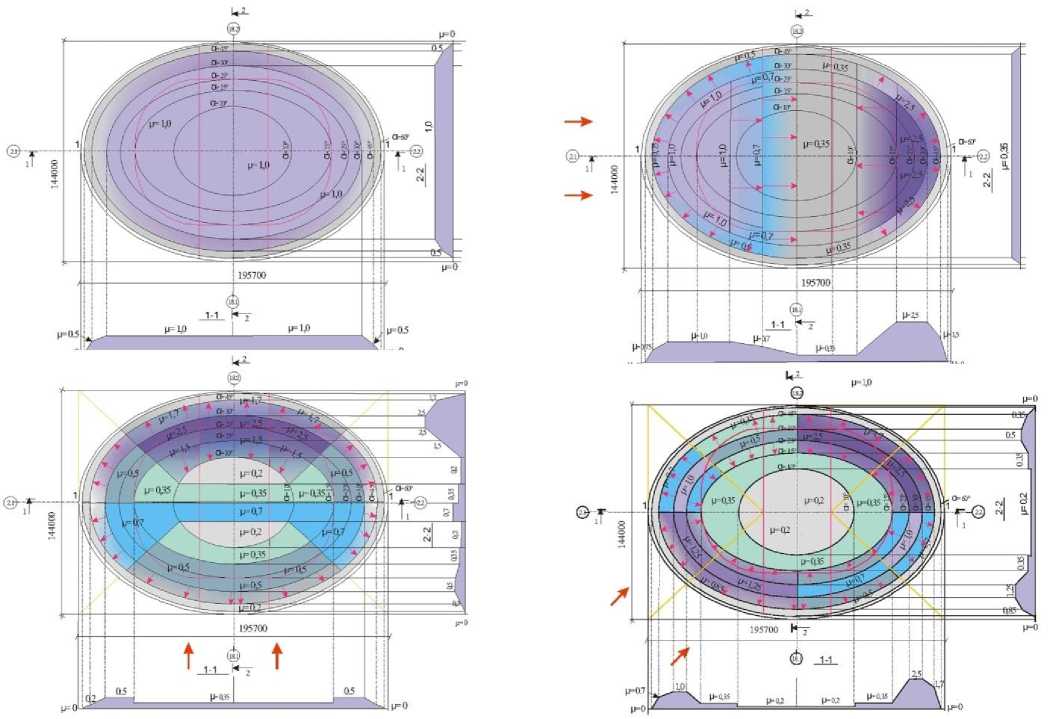
Рисунок 9. Варианты снеговых загружений

Ветровая нагрузка расчитываласт по СП “Нагрузки и воздействия” с использованием рекомендаций Еврокод 1 «Воздейсвия на конструкции» Часть 1-4 «Ветровые воздействия», как для купола, и прикладывалась на ограждающие элементы по 2 направлениям.

Оболочка, смоделированная пластинами, делилась на участки, в пределах которых нагрузка принималась одинаковой (рисунок 10). Для каждой области заданной ширины рассчитывалась и задавалась средняя ветровая нагрузка для этого участка.

Температурные нагрузки были определены по [38], проверены при помощи сателлита «ВеСТ» и приложены на несущие элементы отдельно для летнего и зимнего времен года.

В рамках выполнения исследовательской части работы сейсмические нагрузки не учитывались.

После введения данных о расчетных сочетаниях нагрузок был выполнен статический расчет.

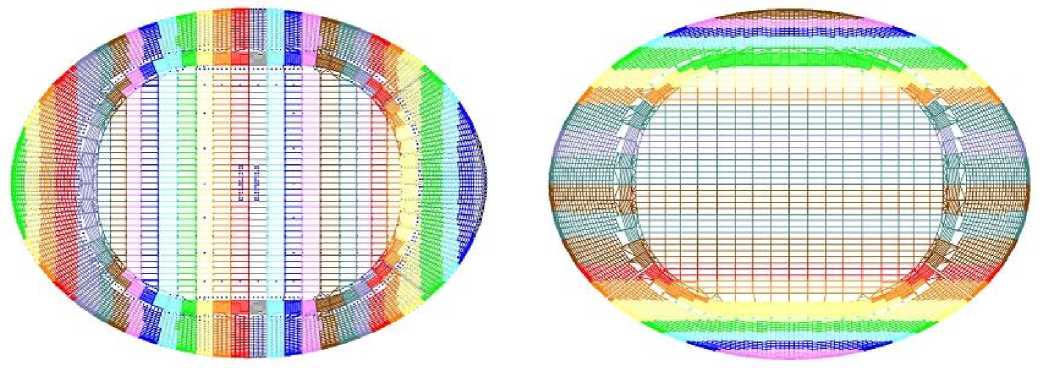
Рисунок 10. Продольное и поперечное разбиение оболочки для ветровых нагрузок в ПК SCAD

Анализ напряженно-деформированного состояния элементов основной арки покрытия

Для анализа напряженно-деформированного состояния покрытия были выбраны наиболее нагруженные элементы верхнего и нижнего пояса, стоек, раскосов. Определен вклад каждой нагрузки для каждой фермы (таблица 1).

Таблица 1. Значения напряжений от различных силовых факторов для элементов ферм, %

Ферма	Постоянная	Технологическая	Снеговая	Температурная	Ветровая
ФС1	25,87	52,47	15,86	1,09	4,71
ФС2	30,05	40,68	21,84	1,20	6,24
ФС3	31,92	35,24	23,22	3,89	5,73
ФС4	32,47	34,58	23,24	3,84	5,87
ФС5	22,44	46,78	23,48	2,52	4,77
ФС6	26,49	43,46	23,61	2,02	4,42
ФС7	24,10	48,72	20,78	2,89	3,51
ФС8	31,23	30,15	30,18	3,83	4,60
ФС9	34,97	12,03	35,46	12,70	4,83
Ср. знач.	28,84	38,23	24,19	3,78	4,96

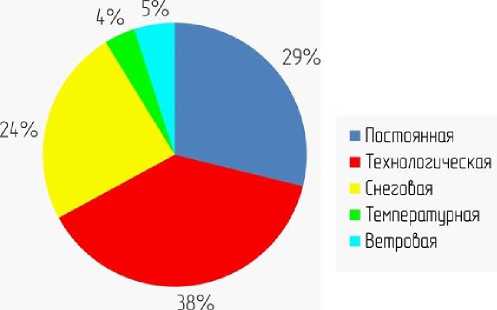
Рисунок 11. Диаграмма соотношения усилий от различных нагрузок

Как видно из рисунка 11 наибольший вклад (38%) в значения нормальных напряжений вносит составляющая от технологических нагрузок.

В указанных фермах проведен анализ распределения продольного усилия в элементах верхнего пояса, возникающего от различных загружений (таблица 2, рисунок 12).

Construction of Unique Buildings and Structures, 2015, №4 (31)

Таблица 2. Продольное усилие N (Т) в элементе верхнего пояса от различных загружений

Ферма	Постоянная	Технологическая	Снеговая	Температурная	Ветровая
ФС1	188,269	260,992	98,691	0,564	30,381
ФС2	172,469	131,038	100,994	0,748	29,957
ФС3	172,114	134,731	107,593	2,831	27,638
ФС4	146,079	113,921	91,633	9,342	23,921
ФС5	153,789	179,51	118,38	3,322	26,1
ФС6	149,822	182,112	116,43	2,766	22,355
ФС7	125,4	102,965	90,597	2,047	14,695
ФС8	112,967	40,937	82,99	0,228	11,738
ФС9	75,519	13,472	57,736	10,603	7,29

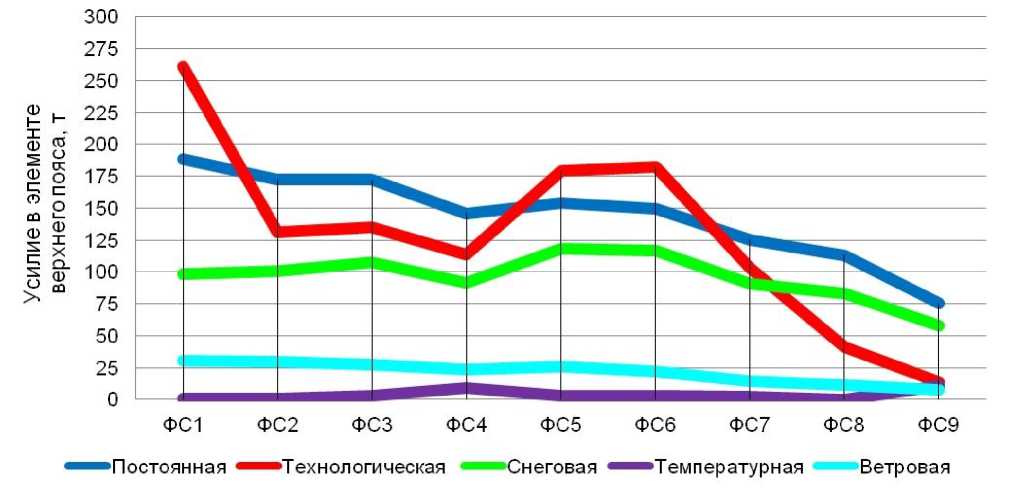
Рисунок 12. График изменения продольного усилия в элементе верхнего пояса

Результаты показывают, что основной вклад в напряженное состояние элементов главной арки принадлежит технологической нагрузке (38%). При этом следует отметить существенную долю собственного веса (29%). Вклад температурной нагрузки(4%) незначителен. Ветровая нагрузка не даёт вклад в расчётное сочетание нагрузок, т.к. вызывает усилия обратного знака.

Выбор целевой функции для решения задач оптимального проектирования

Исходя из особенностей расчета и проектирования, а также учитывая практические вопросы, можно сформулировать одну из основных задач оптимального проектирования металлических конструкций: определить оптимальные геометрические параметры статически неопределимой системы при условии введения в лишние связи начальных усилий.

Проблемы оптимизации металлических конструкций освещены в работах Лихтарникова Я. М. [38], Холопова И. С. [39-41] и ряда других авторов [35, 36]. В общем случае, решение таких задач является весьма сложным, что обуславливается нелинейностью их постановки и определенными трудностями математического описания. Если исходить из тех же критериев и ограничений, которые обычно принимаются при решении задач оптимального проектирования конструкций, то нетрудно убедиться в том, что целевая функция в рассматриваемом случае является нелинейной. Обычно в качестве целевой функции принимают выражение для объема, массы или стоимости материала конструкции, записанные в зависимости от неизвестных задачи [42].

В процессе исследования оценивалась металлоемкость покрытия центральной хоккейной площадки и всей конструкции покрытия.

Для вычисления фактической металлоемкости расчетных моделей, необходимо было произвести не только расчет, но и подбор сечений в каждой из полученных схем, включающих в себя около 4300-5200 элементов каждая. В связи с огромным объемом необходимых вычислений, для упрощения задачи сравнения были приняты следующие гипотезы:

• -    соотношение жесткостей от схемы к схеме меняется незначительно. Следовательно, можно считать, что соотношение жесткостей исходной схемы дает достаточно (для вариантного анализа) достоверную картину распределения усилий по элементам.

• -    все элементы конструкции выполнены из стали с одинаковыми механическими характеристиками.

Произведён подбор сечений (вручную и с использованием постпроцессора ПК SCAD) для двух альтернативных вариантов, также подбор при поиске оптимальной высоты покрытия для каждого из них.

Поиск рациональной геометрической схемы конструкций покрытия

В рамках исследовательской части работы были разработаны две альтернативные конструктивные схемы покрытия над ледовой площадкой. Для каждой из схем была решена задача поиска рациональных геометрических параметров при изменении расстояния между поясами несущих элементов при неизменной геометрии верхнего пояса.

Анализ моделей покрытия производился путем сравнения их металлоемкости и жесткости.

Вариант 1 – Покрытие с радиально расположенными фермами

Покрытие вестибюлей и галерей остается неизменным, в качестве покрытия центральной хоккейной площадки предложена система из 48 радиально расположенных арочных ферм с углом поворота 7.5 ̊ (рисунок 13). Система радиальных ферм имеют центральное опорное кольцо по нижнему и верхнему поясу радиусом 11,46 м. Геометрия ферм полностью повторяет эллипсоидальную форму купола. Длина арочных ферм варьируется от 35,74 до 52 м, высота в наружной опорной зоне от 1 до 3,7 м. в центральной части – 11,74 м.

Общая устойчивость конструкции покрытия обеспечивается системой горизонтальных связей по нижнему поясу на границе каждой панели, вертикальных крестовых связей, прогонов, наружным опорным кольцом.

Пояса ферм неразрезные, узлы сопряжения поясов c центральным опорным кольцом – жесткие, узлы сопряжения раскосов, связей с поясами и системой связей принимаем шарнирным.

Опоры центральных ферм выполнены линейно-шарнирно-подвижными. Элементы ферм были унифицированы подобно проектному решению.

Для подбора сечений элементов используем постпроцессор ПК SCAD. Постпроцессор предназначен также для проверки несущей способности (рисунок 13) стержневых элементов стальных конструкций в соответствии с требованиями СП 16.13330.2011 «Стальные конструкции».

Construction of Unique Buildings and Structures, 2015, №4 (31)

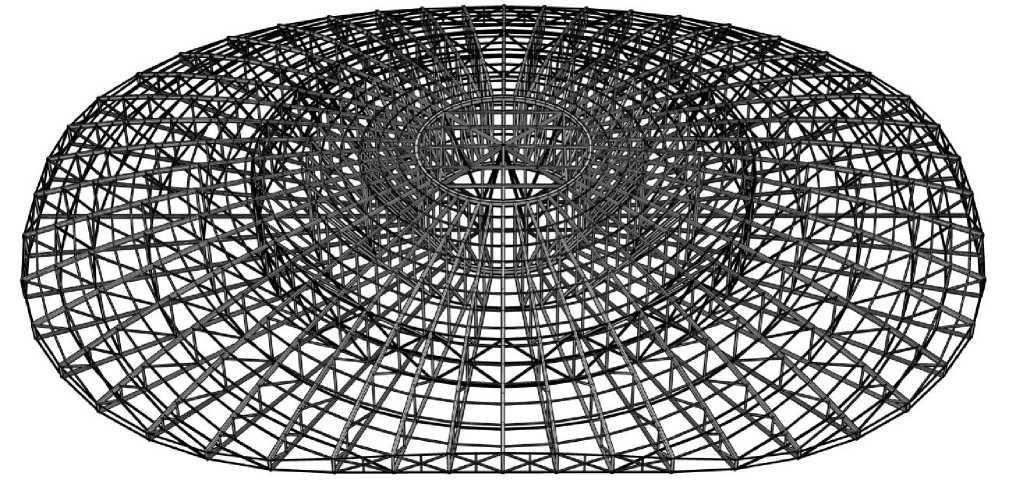
Рисунок 13. Презентационная графика расчетной модели

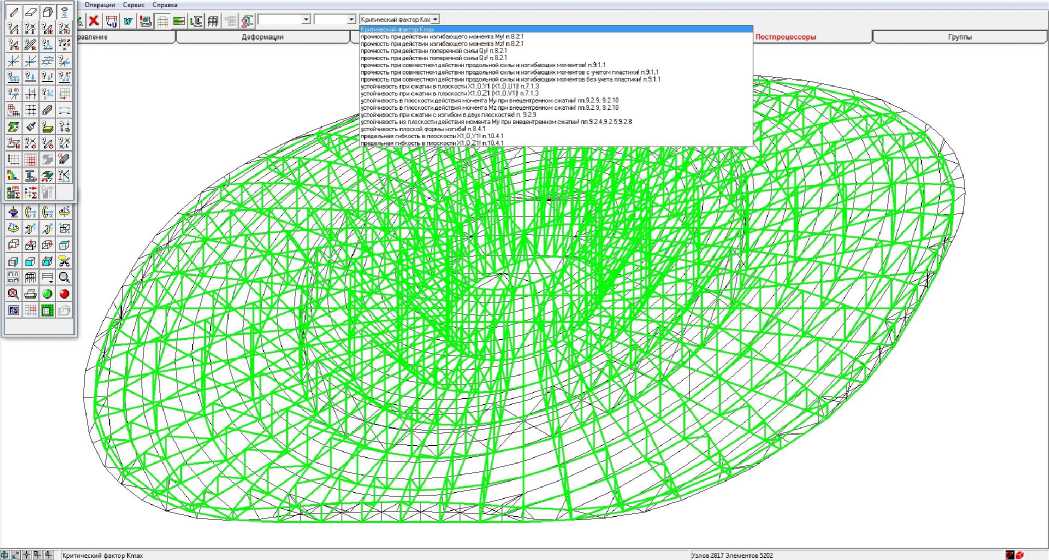
Рисунок 14. Визуализация расчёта постпроцессоров несущей способности

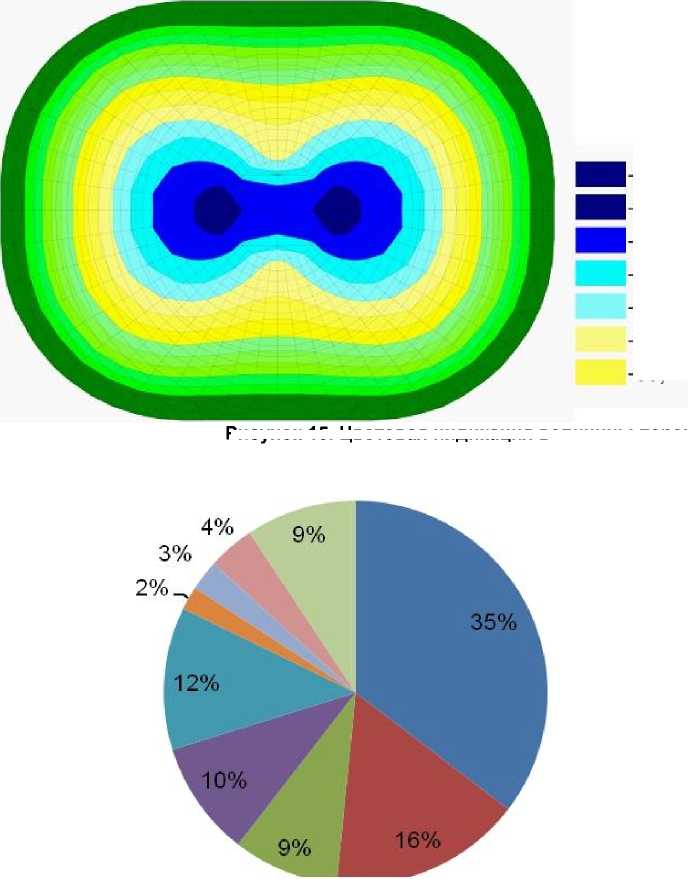
Максимальные значения перемещений находим от нормативных значений собственного веса несущих конструкций и длительных технологических нагрузок (рисунок 15).

■ Верхний пояс

■ Нижний пояс

■ Центр кольцо

■ Наружнеекольцо

■ Связи по нижнему поясу

■ Подвес куба

Прогоны и вертикальные связи

■ Раскосы

■ Стойки

Рисунок 16. Массовая доля конструктивных элементов покрытия с радиальными фермами

1-139,08	-139,08	-79,47	-69,54
-139,08	-129,15	-69,54	-59,61
-129,15	-119,21	-59,61	-49,67
-119,21	-109,28	-49,67	-39,74
-109,28	-99,34	-39,74	-29,8
-99,34	-89,41	-29,8	-19,87
-89,41	-79,47	■1-19,87	0

Рисунок 15. Цветовая индикация величины перемещений, мм

Созданы модели несущих конструкций покрытия, отличающиеся положением нижнего пояса ферм. Модели были созданы по следующим критериям:

• -    тип сечения элементов ферм остаётся неизменным;

• -    положение верхнего пояса ферм остается неизменным.

Для первоначального анализа создавалось 9 моделей. При этом шаг изменения высоты составлял 0,5м.

Для всех полученных моделей были посчитаны значения металлоемкости и прогиба, по которым впоследствии был построен график (рисунок 17). В интервалах появления локальных экстремумов частота шага изменения параметров оптимизации уменьшалась с целью уточнения точки экстремума.

Отдельно рассчитывалось изменение массы каждого конструктивного элемента.

Исходная высота покрытия, равная 11,74 м, является оптимальной высотой по металлоемкости

Construction of Unique Buildings and Structures, 2015, №4 (31)

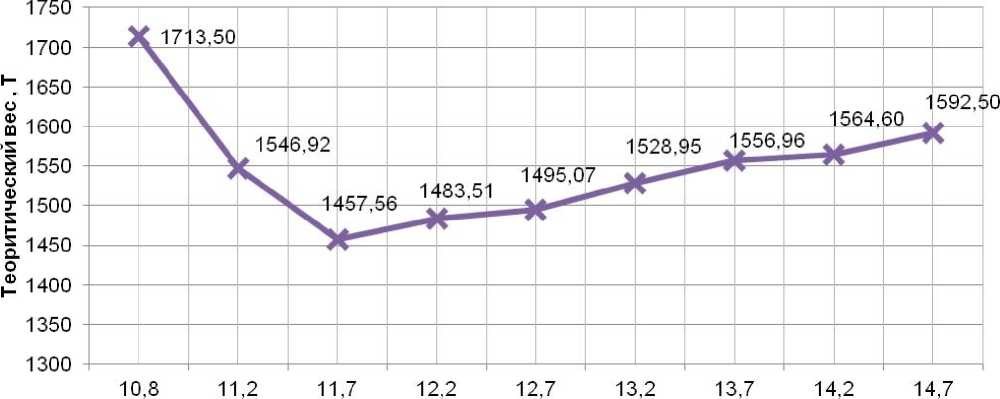
Высота фермы, м

Рисунок 17. График зависимости металлоемкости покрытия радиальных ферм от ее высоты

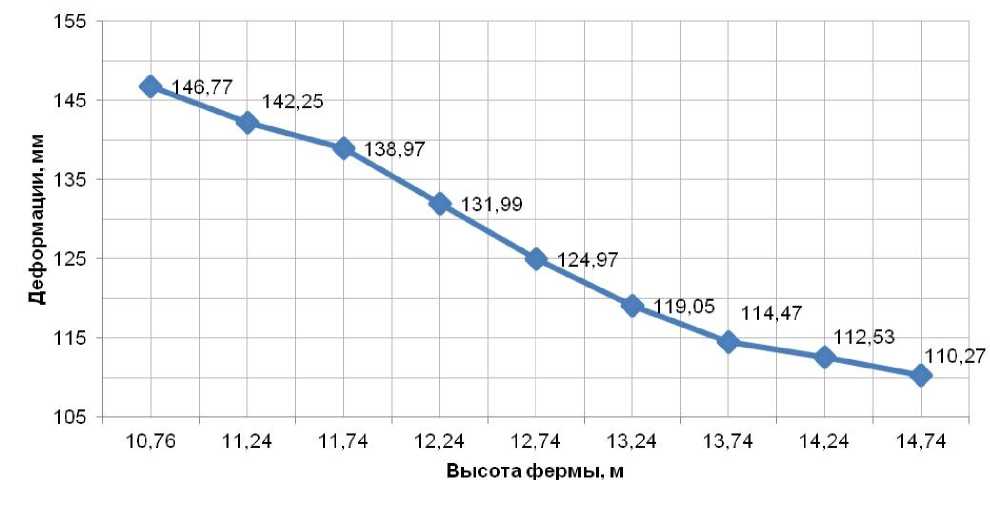
Рисунок 18. График зависимости прогиба покрытия радиальных ферм от ее высоты

Вариант 2 – Покрытие с перекрёстными фермами

Покрытие вестибюлей и галерей остается неизменным, в качестве покрытия центральной хоккейной площадки предложена система из перекрестных 30 ферм повторяющую геометрию эллипсоидального купола. 13 перпендикулярных к основным ферм выполнены с нисходящим раскосом. Шаг этих фермы равен расстоянию между стойками основных ферм.

Длина арочных ферм варьируется от 53,7 до 125,4 м, высота в наружной опорной зоне от 1 до 3,7м. в центральной части – 11,74м.

Пояса исходных фермы неразрезные, пояса перпендикулярных к ним ферм выполнены шарнирно сопряженными с поясами основных ферм. Стойки и раскосы примыкают шарнирно.

Элементы ферм были унифицированы подобно проектному решению.

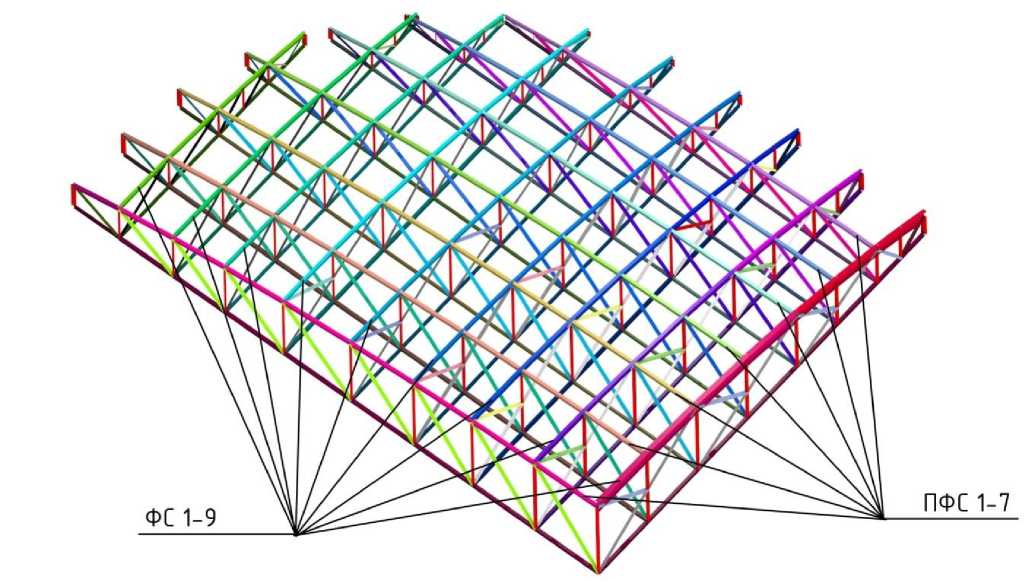
Рисунок 19. Четверть покрытия с цветовой индикацией унифицированных элементов

Для подбора сечений элементов использован постпроцессор ПК SCAD.

Максимальные значения перемещений определялись от нормативных значений собственного веса несущих конструкций и длительных технологических нагрузок (рисунок 20).

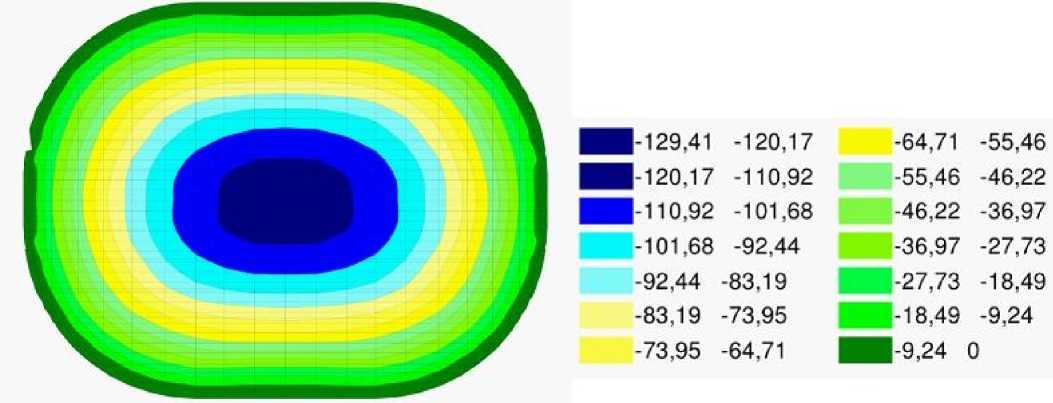
Рисунок 20. Цветовая индикация величины перемещений, мм

Созданы модели несущих конструкций покрытия, отличающиеся положением нижнего пояса ферм. Модели были созданы по следующим критериям:

• -    тип сечение элементов ферм остаётся неизменным;

• -    положение верхнего пояса ферм остается неизменным.

Для первоначального анализа создавалось 6 моделей. При этом шаг изменения высоты составлял 0,5м.

Для всех полученных моделей были посчитаны значения металлоемкости и прогиба, по которым впоследствии был построен график (рисунок 21). В интервалах появления локальных экстремумов частота шага изменения параметров оптимизации уменьшалась с целью уточнения точки экстремума.

Отдельно рассчитывалось изменение массы каждого конструктивного элемента.

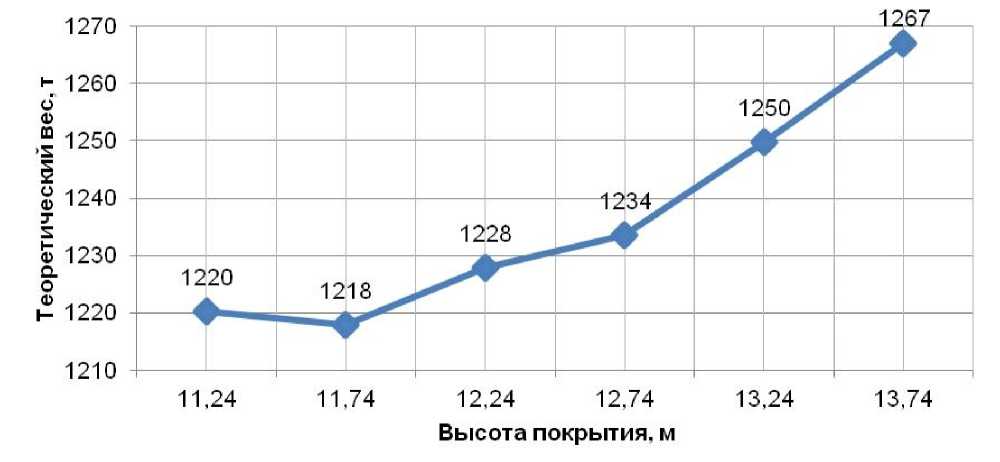
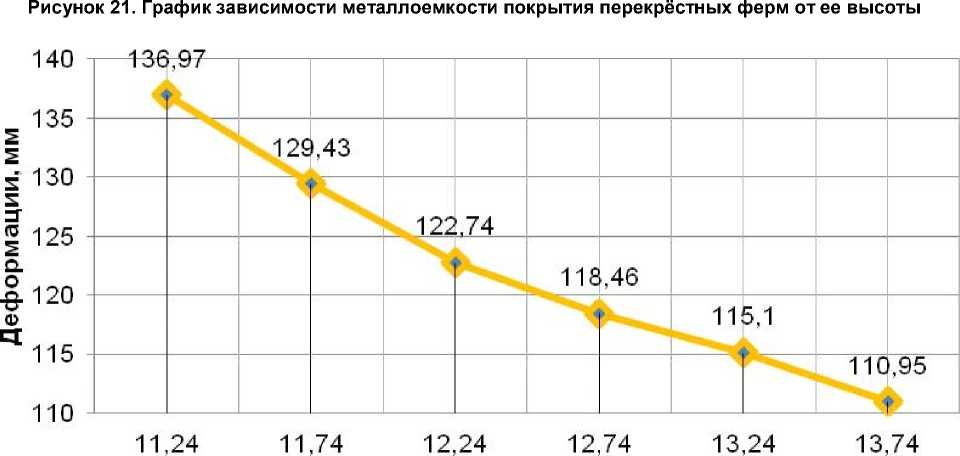
Высота покрытия, м

Рисунок 22. График зависимости прогиба покрытия перекрёстных ферм от ее высоты

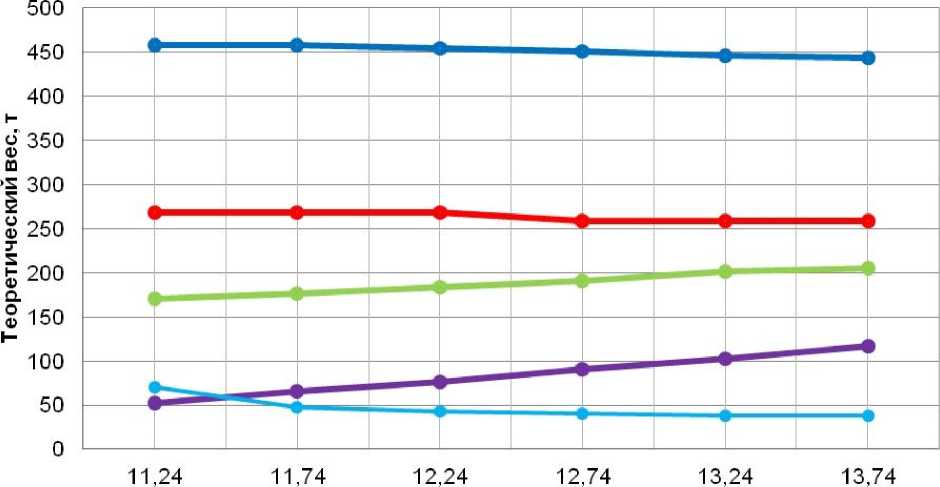
Высота покрытия, м

^^—Верхний пояс ^^•Нижнии пояс —^Раскосы ^^—Стоики • Опорное кольцо

Рисунок 23. График изменения массы элементов покрытия

Исходная высота покрытия, равная 11,74 м, является оптимальной высотой по металлоемкости.

Сравнение вариантов покрытия

В результате подбора сечений различных конструкций покрытия были определены их фактические массы и прогибы. Данные характеристики представлены в таблице 3.

Таблица 3. Результаты вариантного проектирования

Вариант покрытия	Прогиб, мм	Фактическая масса, т
Исходный вариант покрытия	136,89	1179,16
Покрытие перекрестными фермами	129,43	1217,92
Покрытие с радиальными фермами	138,97	1020,35

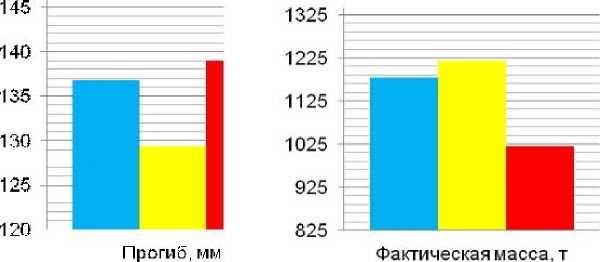
■ Исходный вариант покрытия

Покрытие перекрестными фермами

■ Покрытие с радиальными фермами

Рисунок 24. Сравнение вариантов покрытия по металлоемкости и прогибу

Construction of Unique Buildings and Structures, 2015, №4 (31)

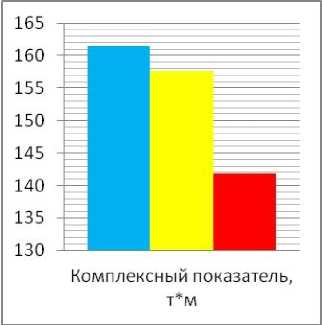
Рисунок 25. Сравнение вариантов покрытия по условному комплексному показателю

Условный     комплексный     показатель,     полученный перемножение прогиба на соответствующую металлоемкость, показывает, что покрытие с радиальными фермами эффективнее других вариантов покрытия.

Выводы

• 1.   Выполнено создание КЭ модели несущих металлических

• 2.   Произведен анализ напряженно-деформированного

• 3.   При помощи предложенного алгоритма решены две

• 4.   Анализ различных конструктивных схем покрытия, показал, что наиболее оптимальным

конструкций покрытия ледового дворца “Большой” с использованием ПК SCAD совместно с другими программными комплексами.

состояния элементов главной арки покрытия на различные нагрузки и воздействия. Структурный анализ состава напряжений в наиболее нагруженных элементах показал, что наибольшие напряжения возникают от технологических нагрузок (38% от максимальных), а основным силовым фактором в стержневых элементах является продольное усилие N.

задачи по поиску рационального решения методом вариантного проектирования. При исследовании влияния высоты сооружения на его металлоемкость (вторая задача) определено, что наиболее рациональная высота покрытия, для рассмотренных вариантов – 11,74 м (проектная высота).

решением, в условиях принятых допущений, является покрытие с радиально расположенными фермами.