Анализ RANS моделей турбулентности на примере расчёта стационарного течения в отсасывающей трубе гидротурбины Turbine-99

Отсасывающая труба представляет собой часть проточного тракта гидравлической электростанции, соединяющую гидротурбину с нижним бьефом и предназначенную для преобразования остаточной кинетической энергии воды в энергию давления [1]. Поток, поступающий сюда после прохождения гидротурбины, обладает закруткой, степень которой зависит от режима работы турбины. Закрутка потока, с одной стороны, предотвращает отрыв потока от стенок отсасывающей трубы, с другой стороны, может вызывать крупномасштабные пульсации давления в потоке вследствие прецессии вихревого ядра, приводящие к вибрациям конструкций и снижающие их надёжность. На отсасывающую трубу приходится существенная часть потерь энергии в проточном тракте гидравлических электростанций. Характеристики отсасывающей трубы необходимо знать для определения кавитационных параметров гидротурбины. В связи с этим исследование гидродинамических процессов в отсасывающих трубах представляет собой чрезвычайно актуальную задачу как с практической, так и фундаментальной точки зрения.

Подробные экспериментальные исследования течения в отсасывающей трубе проводились в рамках международного проекта Turbine-99 на стенде в лаборатории города Alvkarleby (Швеция). Стенд представляет собой уменьшенную модель гидротурбины Holleforsen [2], с помощью которой можно выполнить измерения скорости и давления в отсасывающей трубе. Обсуждению экспериментов и установленных в 1999–2005 г. результатов было посвящено три специальных семинара [3–5].

На третьем семинаре организаторы унифицировали некоторые детали постановки исследований. Расчетные распределения коэффициента давления вдоль трубы хорошо соответствовали экспериментальным данным, однако интегральные характеристики имели большую погрешность. Сравнение профилей скорости в конусе отсасывающей трубы показало, что расчёты завышают ширину зоны рециркуляции на оси трубы, а вычисленное значение тангенциальной скорости за обтекателем рабочего колеса получается значительно выше измеренного.

В [6] представлены расчёты течения в турбине с учётом рабочего колеса и отсасывающей трубы. Одной из целей работы было моделирование течения в зазоре между лопастью и обтекателем рабочего колеса, и автору удалось показать, что при принятии во внимание зазора в профиле аксиальной компоненты скорости на входе в отсасывающую трубу появляется локальный экстремум вблизи обтекателя рабочего колеса.

В 2007 г. другими авторами (см. [7]) были проведены измерения скорости в тех же сечениях и при тех же условиях, что и в [2]. Профили компонент скорости на входе получились близкими к данным работы [2], за исключением участка около рабочего колеса. Вблизи стенки обтекателя рабочего колеса наблюдался локальный экстремум аксиальной скорости. В следующем за входом сечении профили аксиальной компоненты скорости хорошо совпали с измеренными в [2], а значение тангенциальной скорости оказалось выше, что качественно соответствует результатам публикации [6].

В данной работе осуществляется моделирование стационарного течения в отсасывающей трубе гидротурбины, которой посвящён проект Turbine-99. Граничными условиями служат экспериментальные данные из [7]. Для реализации используется код SigmaFlow [8]. Целью настоящего исследования являются сравнение и анализ границ применимости современных RANS моделей турбулентности (Reynolds Averaged Navier-Stokes Equations — усредненных по Рейнольдсу уравнений Навье–Стокса) для описания закрученного потока в отсасывающей трубе.

2.    Постановка задачи

Рассматриваемая отсасывающая труба представляет собой часть уменьшенной модели турбины Holleforsen. Турбина относится к поворотно-лопастному типу (турбина Каплана), рабочее колесо имеет пять лопастей. Моделируемая область (Рис. 1) начинается немного ниже лопастей рабочего колеса и включает его обтекатель. Начальный участок трубы представляет собой конус. Так как течение в этом конусе близко к осесимметричному, то для его сечений 1a и 1b используются полярные координаты r (радиальная) и z (аксиальная). При этом ось z направлена вверх, как показано на рисунке 1, б . В экспериментальном стенде отсасывающая труба выходит в широкий бак, но при моделировании расчётная область ограничивается выходом из отсасывающей трубы (Рис. 1).

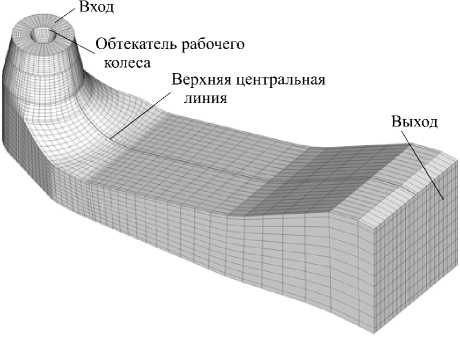
а

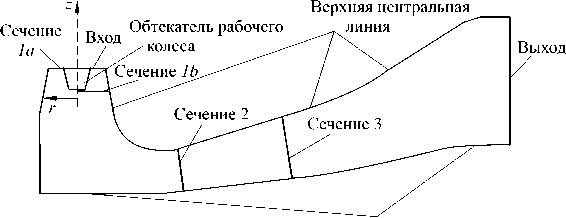
Нижняя центральная линия

Рис. 1. Отсасывающая труба Turbine-99: пример расчётной сетки ( а ), схема расчётной области ( б )

б

В расчётах использовались профили аксиальной W ( r ) и тангенциальной V ( r ) компонент скорости v на входе (в сечении 1a ), измеренные в [7]. Профиль аксиальной компоненты скорости на входе приведен на рисунке 2. Для сравнения на том же рисунке показан профиль скорости, полученный в [2]. Профили отличаются локальным экстремумом скорости вблизи обтекателя рабочего колеса, наблюдаемым в [7]. Профиль тангенциальной компоненты скорости на входе совпадает с результатом из [2]. Радиальная компонента скорости U ( r ) рассчитывалась по аксиальной с учётом условия, что течение вблизи стенок обтекателя и отсасывающей трубы параллельно этим стенкам. Пусть 9 — угол между направлением скорости на входе и нормалью к входному сечению. Линейная интерполяция угла 9 дает следующее выражение для радиальной компоненты: U ( r ) = - W ( r ) tg( 9 ), 9 = 9 c + ( 9 w -9 c )( r - R c )/( R w - R c ) ,

9c =-12,8°,  9w = 2,8°,  Rc = 0,0981 м, Rw = 0,2365 м, 9w = 2,8° , где 9c — угол наклона обтекателя рабочего колеса, 9w — угол наклона стенки отсасывающей трубы, Rc — радиус обтекателя рабочего колеса во входном сечении, Rw — радиус входа, м.

Так как пульсационные составляющие скорости в [7] не измерялись, то для определения турбулентных характеристик на входе использовались данные из сборника [5]. Распределение энергии турбулентных пульсаций вычислялось на основе экспериментальных значений среднеквадратичных пульсаций v и w на входе и условия u = v, где u, v, w — среднеквадратичные отклонения радиальной, тангенциальной и аксиальной компонент скорости соответственно. Таким образом, распределение кинетической энергии турбулентных пульсаций на входе определялось по формуле: k = (w2 + 2v2)/2. Скорость диссипации энергии турбулентных пульсаций, исходя из масштаба турбулентных вихрей, составляла: е = CЦ4 (к3/2/1), где Cц — константа модели, Cц = 0,09.

Масштаб турбулентных вихрей оценивался по экспериментальным значениям турбулентных напряжений, скорости и энергии турбулентных пульсаций на входе. Масштаб турбулентных вихрей равнялся 1 = 0,02 м.

Профиль скорости корректировался с учётом фактического расхода во входном сечении 0,522 м3/с [4],

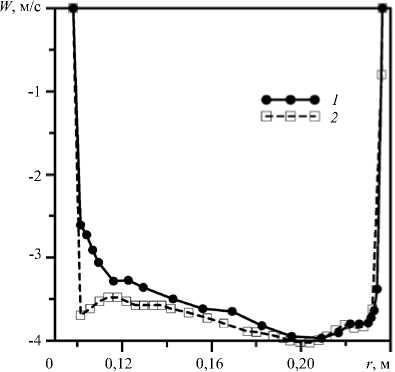
Рис. 2. Аксиальная компонента скорости на входе в отсасывающую трубу; 1 – измерения [2], 2 – измерения [7]

то есть все компоненты скорости умножались на коэффициент, равный отношению расхода 0,522 м3/с к

интегралу от аксиальной компоненты скорости по площади

входа. Согласно [7] поправка составляет 2%. На рисунке 2 приведён скорректированный профиль скорости. Скорость вращения рабочего колеса составляла 595 об/мин. Закрутка

потока вычислялась по

приближённой

формуле

w

S w

W ² rdr

= 0,25 .

Сравнение результатов расчётов с экспериментальными данными проводилось для распределения давления вдоль верхней и нижней центральных линий и для распределения скорости в сечении 1b . Данные линии идут вдоль стенки отсасывающей трубы от входа в расчётную область до выхода из неё (Рис. 1). Для сечения 1b распределение рассматривалось вдоль линии, соответствующей азимутальному углу а = 270 ° (где а — угол, отсчитываемый от направления потока в хвостовой части трубы), что соответствует положению датчиков в эксперименте [7].

3.    Модель

Расчёты проводились в программном комплексе SigmaFlow [8], развиваемом специалистами Института теплофизики СО РАН (г. Новосибирск) и Сибирского федерального университета (г. Красноярск). Данный программный комплекс предназначен для решения задач гидродинамики, тепломассообмена и горения и обеспечивает все этапы решения: построение геометрической модели и расчётной сетки, собственно вычисления и анализ результатов с использованием широкого набора графических средств.

Задача исследования турбулентного течения несжимаемой жидкости состоит в решении уравнений Рейнольдса:

V-v = 0,       р( v-V) v = -Vp + V- (т m +t t),

где т

— тензор вязких напряжений с компонентами т j = ц

Гдv,   д v )

— + — j- д x j   д x i

, а т — тензор рейнольдсовых

напряжений с компонентами т j = ц t

■ д г ₊d vj' д x j   д x i

35 j-р k

Уравнения Рейнольдса замыкаются с помощью одной из следующих моделей турбулентности:

стандартной к -е модели; к -е модели Чена [9], к -го SST (shear stress transport — переноса сдвиговых напряжений) модели Ментера [10], модели Спаларта–Аллмареса (SA — Spalart–Allmaras), а также моделей SARC [11] (Spalart–Allmaras rotation correction — модели Спаларта–Аллмареса с коррекцией на закрутку потока) и к -го SST-CC [12] (curvature correction — с коррекцией на кривизну линий тока), учитывающих закрутку потока. Тестирование задач течения закрученных потоков, описываемых с помощью данных моделей, ранее рассмотрено в статье [13]. Для моделирования граничных условий на твердых границах расчётной области используется метод пристеночных функций. Безразмерное расстояние до стенки на измельчённой сетке составляет у + ® 300 .

Следует заметить, что учёт закрутки потока в моделях SARC и к -го SST-CC осуществляется с помощью специальных коэффициентов в уравнениях для турбулентных характеристик. С этой целью в модели SARC в член уравнения переноса модифицированной вязкости, определяющий генерацию, добавляется поправочный коэффициент, введенный Шуром и др. [11], который описывает влияние на турбулентность кривизны линий тока. В модели к -го SST-CC аналогичный множитель включается в члены генерации в уравнениях к и го модели к -го SST Ментера, что соответствует модели, предложенной в работе [12]. Данное преобразование является распространением поправки на кривизну линий тока, вводимой в модели SARC, на модель к -го SST.

На выходе из отсасывающей трубы задавались условия Неймана для всех величин. Решение системы уравнений, описывающих течение несжимаемой жидкости, производилось с помощью процедуры расщепления SIMPLEC (Semi-Implicit Method for Pressure-Linked Equations — полунеявного метода для связывающих давление уравнений) [14, 15]. Дискретизация уравнений переноса основывалась на методе конечных объемов. Применялись блочно-структурированные расчётные сетки, состоящие из гексаэдральных ячеек. Конвективные члены в уравнении импульса аппроксимировались с помощью схемы Quick [15], а в уравнениях турбулентных характеристик — с помощью схемы Umist TVD (Total Variation Diminishing — уменьшения полной вариации) [15].

4.    Результаты

В сборнике [5] представлены экспериментальные распределения коэффициента давления вдоль нижней и верхней центральных линий (см. Рис. 1): C p = ( p - p_inwall )Д ( р/ 2 )( Q/A n ) 2 ) , где Р — давление в текущей точке на верхней или на нижней линии, p_{in: wall} — среднее давление по периметру входа, р — плотность воды, Q — расход во входном сечении, A n — площадь входа. Распределение коэффициента давления вдоль трубы нормировалось таким образом, чтобы на выходе было C_p = 1. Для интегральной характеристики работы отсасывающей трубы использовался коэффициент восстановления давления, который находился следующим образом: ^Cpwall = ( P out^di - P n.wdl )/( ( Р/ ² )( QtA in ) 2 ) , где P out.wall ^— среднее д^{авление по} периметру выхода; значения среднего давления по сечениям входа–выхода оценивалось по давлению в точках расположения датчиков в эксперименте (по восьми точкам на стенке при входе и одиннадцати — на выходе). Интегральные характеристики ( C_p — коэффициент восстановления давления, определяемый по сечениям входа– выхода, и Z — коэффициент потери энергии) рассчитывались по формулам:

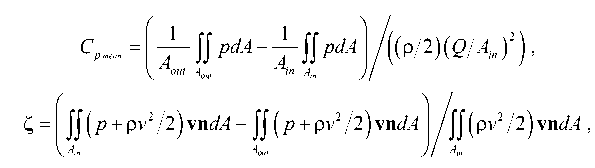
p mean out Ao in out p + рv2/2) vndA - JJ (p + рvv /2)vndA

V A n

A out

A i

у

где n — нормаль к поверхности входа или выхода, A_out — площадь выхода, v — модуль скорости.

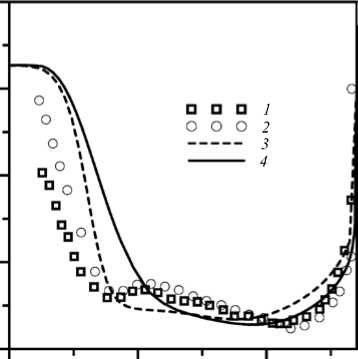
В первую очередь было рассмотрено влияние граничных условий на результаты расчёта. На рисунке 3 приведены профили скорости в сечении 1b, найденные при двух различных постановках: с использованием в качестве граничных условий на входе, соответственно, данных измерений из [7] и [2] (турбулентность описывалась моделью к -го SST). Как видно из рисунка 3, а, вблизи оси трубы аксиальная компонента скорости лучше соответствует экспериментальным данным. Для течения в конусной части об этом можно судить по ширине зоны рециркуляции за рабочим колесом: вблизи оси трубы зона более узкая. Отличие экспериментальных данных для входного сечения от вычисленных состоит в форме профиля аксиальной компоненты скорости: измерения [7] содержат локальный экстремум аксиальной компоненты скорости вблизи стенки обтекателя рабочего колеса, влияющий на формирование зоны рециркуляции за рабочим колесом.

Профиль тангенциальной компоненты скорости в сечении 1b отличается в измерениях [2] и [7] (Рис. 3, б ). В измерениях [2] абсолютная величина тангенциальной компоненты существенно меньше вычисленных. По-видимому, данные [7] точнее, так как лучше удовлетворяют условию консервативности потока момента импульса. Действительно, согласно [7] его величина на входе в отсасывающую трубу и в сечении 1b остается постоянной и составляет 99 кг∙м²/с², в то время как, согласно [2], поток на входе равняется 98 кг∙м²/с², а в сечении 1b его величина падает до 76 кг∙м²/с². В расчёте также соблюдается консервативность момента импульса (102 кг∙м²/с²). Расчётный профиль тангенциальной компоненты скорости (Рис. 3, б ) хорошо согласуется с экспериментальными данными [7], за исключением области вблизи оси конуса.

IF. м/с

О

К, м/с

-0,4

-0.8

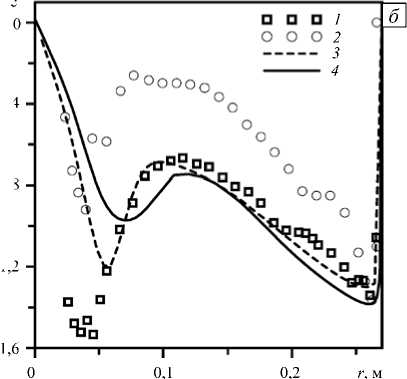
Рис. 3. Аксиальная ( а ) и тангенциальная ( б ) компоненты скорости в сечении 1b ; 1 – измерения [7], 2 – измерения [2], 3 – расчёт с профилем из [7] на входе, 4 – расчёт с профилем скорости на входе по данным из [2]

-1,2

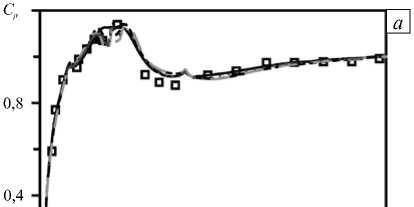
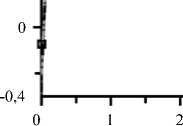
На рисунке 4 приведены распределения коэффициента давления вдоль отсасывающей трубы, полученные на различных расчётных сетках при использовании турбулентной модели к -ю SST. Распределение коэффициента давления вдоль нижней центральной линии показано на рисунке 4, а . Судя по нему, измельчение сетки позволяет повысить точность расчёта течения вблизи точки L = 1,2, находящейся в «пятке» отсасывающей трубы — в месте перехода вертикального канал в горизонтальный. В углу «пятки» образуются вихри, что приводит к появлению минимумов давления на стенке. Расчёты на более мелких сетках свидетельствуют о наличии двух минимумов вблизи угла, соответствующих экспериментальным точкам.

□ □ □ / -------- 2

-----3

• • • 5

1---------1--------'---------1---------1--------

3        4 L, м

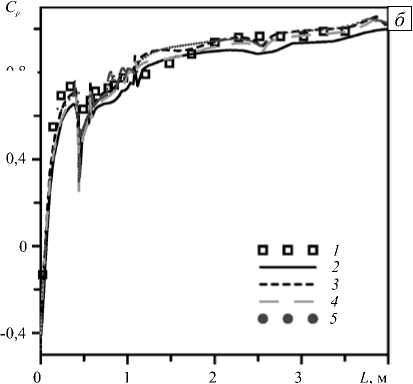
Рис. 4. Распределение коэффициента давления вдоль нижней ( а ) и верхней ( б ) центральных линий; 1 – эксперимент; 2 – расчёт на сетке с 29 тыс. ячеек; 3 – 232 тыс. ячеек; 4 – 830 тыс. ячеек; 5 – 1,1 млн. ячеек

0.8 -

На сетке, содержащей 1,1 млн. контрольных объемов, были проведены вычисления интегральных характеристик закрученного течения с использованием различных моделей турбулентности (см. Табл.). Из таблицы видно, что все расчёты в той или иной степени завышают значение C_pwall . Возможно, это связано с распределением давления на входе. Экспериментальное распределение давления на входе имеет минимум внутри области, а давление на стенке близко к среднему по сечению давлению. В расчётах же минимум давления на входе приходится на стенку (Рис. 5). Соответственно, давление на стенке значительно ниже среднего давления на входе, что приводит к завышению коэффициента восстановления давления. Графики на рисунках 4 и 6 показывают, что найденное распределение давления в остальной части исследуемой области совпадает с экспериментальным. Коэффициент давления, рассчитанный по площади сечения, наоборот, несколько занижается. Все модели, за исключением SA и SARC, дают близкие результаты.

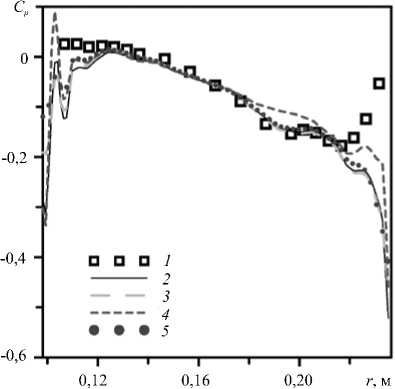
Рис. 5. Экспериментальное (кривая 1 ) и расчетное (кривые 2 – 5 ) распределение коэффициента давления на входе; апробированные модели турбулентности: стандартная k -ε (кривая 2 ), k -ε Чена ( 3 ), SA ( 4 ), k -ω SST ( 5 )

Таблица. Интегральные характеристики в зависимости от модели турбулентности

Тип модели	С „ p wall	с p mean	ζ
Стандартная k -ε	1,37	0,97	0,24
k -ε Чена	1,30	1,00	0,16
SA	1,30	0,88	0,28
k -ω SST Ментера	1,28	0,99	0,18
SARC	1,28	0,93	0,26
k -ω SST-CC	1,25	0,98	0,22

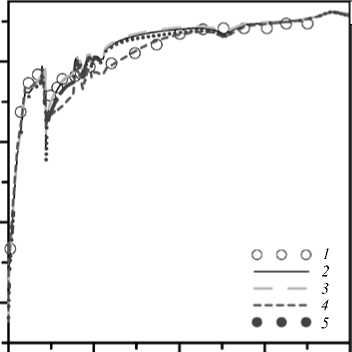
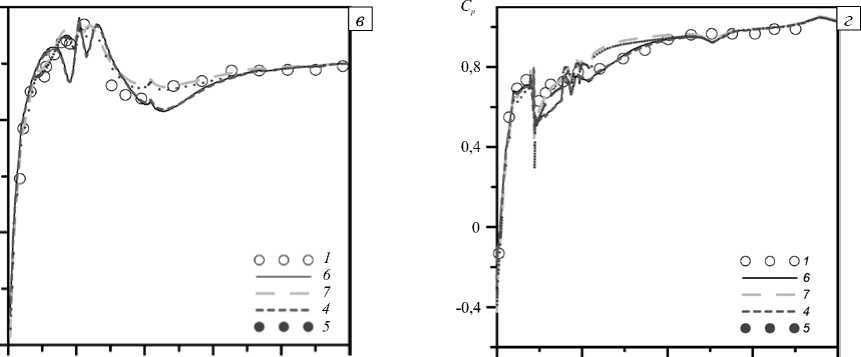
Близким для всех моделей получается и распределение коэффициента давления по длине трубы (Рис. 6). Расхождение наблюдается в углу «пятки»: модели k -ε стандартная и k -ε Чена не воспроизводят два максимума давления вдоль нижней центральной линии; модель Спаларта–Аллмареса даёт дополнительные экстремумы коэффициента давления в области изгиба и занижает падение давления после него. Наилучшее совпадение распределения давления вдоль нижней центральной линии имеет место при модели k -ω SST.

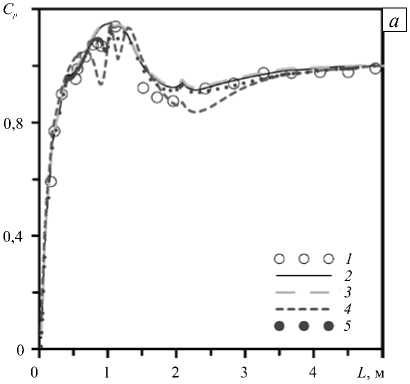
Рис. 6. Экспериментальное (кривая 1 ) и расчетное (кривые 2 – 7 ) распределение коэффициента давления вдоль нижней ( а , в ) и верхней ( б , г ) центральных линий; апробированные модели турбулентности: стандартная k -ε (кривая 2 ), k -ε Чена ( 3 ), SA ( 4 ), k -ω SST ( 5 ), SARC ( 6 ), k -ω SST CC ( 7 )

с„

0,8

0,4

-0,4

б

2           3        £, м

0,8

0,4

О

О

Рис. 6. Продолжение

4 L, м

Профиль аксиальной компоненты скорости в

сечении 1b получается близким для всех моделей

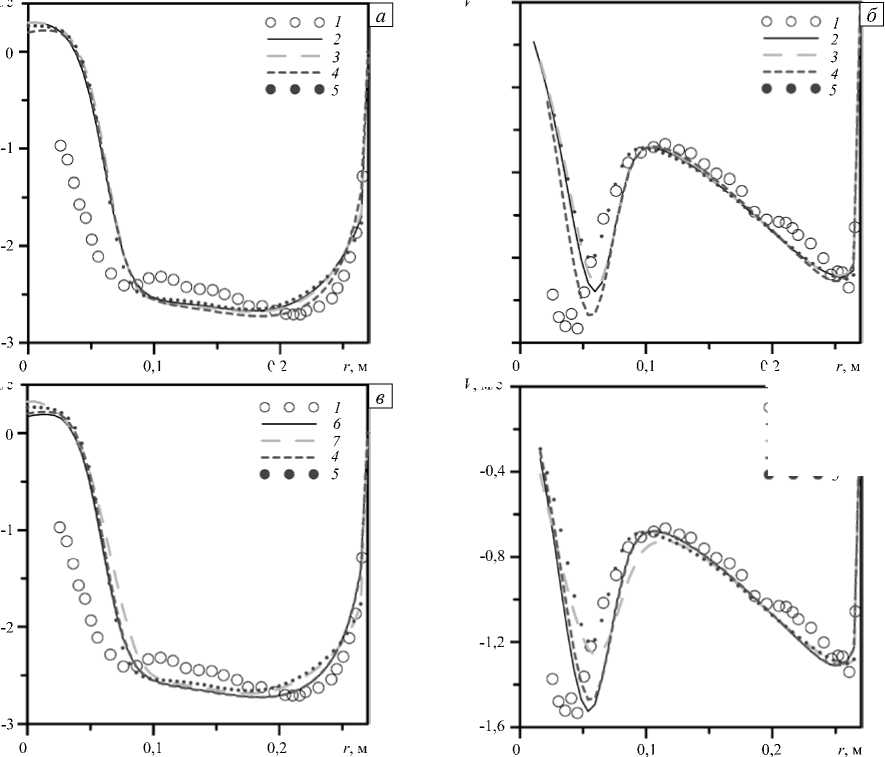
(Рис. 7, а , в ). Во всех расчётах зона рециркуляции имеет одинаковую ширину. Небольшое отличие наблюдается вблизи стенки отсасывающей трубы: модель SA точнее воспроизводит пристеночную область течения. Для тангенциальной компоненты скорости различие между результатами при разных моделях является несущественным в области свободного вихря (0,1 <  r <  0,25) (Рис. 7, б , г ). На границе вынужденного вихря ( r = 0,05 м) модель SA даёт наибольшую абсолютную величину тангенциальной компоненты скорости. Применение поправки на закрутку потока влияет на результаты несущественно (Рис. 6, в , г ; Рис. 7, в , г ).

IV, м/с

V, м/с

-1.6

И, м/с

-0,4

-0,8

-1.2

W, м/с

0,2

0,2

ООО/

------- 6 7

-----4

е е е 5

г

Рис. 7. Аксиальная ( а , в ) и тангенциальная ( б , г ) компоненты скорости в сечении 1b для разных моделей турбулентности: стандартная к -s (кривая 2 ), к -s Чена ( 3 ), SA ( 4 ), к -ш SST ( 5 ), SARC ( 6) , к -ш SST CC ( 7 ); кривая 1 - эксперимент

5.    Заключение

В работе было проведено численное моделирование течения в отсасывающей трубе Turbine-99 с использованием различных моделей турбулентности. Показано, что на достоверность расчётов существенное влияние оказывает постановка граничных условий на входе. Использование в качестве профиля скорости на входе данных [7] позволило точнее описать течение в конусе отсасывающей трубы. Об этом свидетельствует ширина зоны рециркуляции: в этом случае она меньше, чем вычисленная на основе данных [2].

Выполненные расчёты показали, что в конусе отсасывающей трубы рассмотренные RANS модели, в целом, дают близкие результаты, удовлетворительно согласующиеся с данными экспериментов [7]. В начальной области отсасывающей трубы лучше описывают течение модели SA и, особенно, SARC: они точнее воспроизводят как аксиальную компоненту скорости вблизи стенки отсасывающей трубы, так и профиль тангенциальной компоненты скорости. В то же время распределение давления, вычисленное по моделям SA и SARC, в области «пятки» и после ее прохождения существенно отклоняется от экспериментальных данных, что говорит о формировании более многочисленных и интенсивных вихрей в изгибе отсасывающей трубы. Такие модели как k -ε стандартная и k -ε Чена и вовсе не воспроизводят здесь минимум давления. Поскольку в соответствующих режимах поток закручен слабо, влияние коррекции на закрутку потока [11, 12] в этом случае незначительно. По итогам проведённого исследования наилучшие результаты продемонстрировала модель k -ω SST, которая позволяет получить корректное распределение давления и хорошо описывает течение на начальном участке.

Работа выполнена при финансовой поддержке федеральной целевой программы «Научные и научнопедагогические кадры инновационной России» на 2009-2013 годы и грантом Правительства России № 11.G34.31.0046 государственной поддержки научных исследований, проводимых под руководством ведущих ученых в российских вузах (ведущий ученый — К. Ханъялич, НГУ, г. Новосибирск).