Анализ распределения посевного материала по площади поля

Введение. Сошники для разбросного посева семян, устанавливаемые на сеялку, должны иметь такую конструкцию и размеры, при которых достигается наилучшее распределение семян по площади поля. Равномерное распределение семян по площади питания играет основную роль в создании условий для произрастания растений.

Для получения более равномерного распределения семян по площади под выходным отверстием стойки-семяпровода сошника размещают различные разбрасыватели семян.

Цель исследования: изучить закономерности распределения семенного материала по площади поля лаповым сошником с обоснованием рациональных конструктивных параметров распределителя семян.

Задачи исследования:

– получить числовые характеристики равномерного пуассоновского распределения семян по площади поля;

– определить закономерности равномерного распределения семян по профилю;

– определить рациональные конструктивные параметры распределителя семян.

Методы исследования . Данное исследование посвящено выбору оптимального профиля поверхности распределителя в классе цилиндрических поверхностей с прямолинейной образующей, описываемых уравнением F ( x , z ) = 0 (рис. 1).

С достаточной для практики точностью форму поверхности распределителя семян можно описать координатами десяти точек (рис. 2).

z

Рис. 1. Общий вид распределителя семян

z

Рис. 2. Схема дискретизации профиля распределителя

A =( Ax, A:) В=( Bx, Bz)

J=( J., J)

Поскольку у точки A = ( A_x , A_z ) координата A_x = 0 , то получаем 19 варьируемых параметров. К числу варьируемых параметров нужно также отнести размеры и количество прорезей, предназначенных для «просеивания» части семян в пространство под распределителем.

В качестве рабочего инструмента для поиска наилучшей формы поверхности разбрасывателя семян нами был выбран лаповый сошник, в подсошниковом пространстве которого установлен разбрасыватель семян [1].

Схема сошника сеялки с размещенным в подсошниковом пространстве разбрасывателем семян показана на рисунке 3.

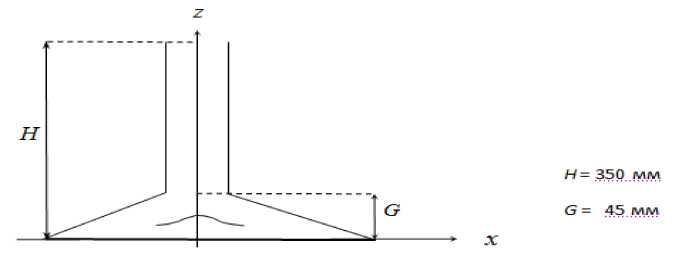
Рис. 3. Схема сошника сеялки:

Н – высота сошника; G – высота распределителя

Рассмотрим процесс распределения семян на плоскости. О качестве распределения семян можно будет судить после расчета элементов их траекторий полета. Распределение можно считать идеальным, если его характеристики соответствуют пуассоновскому распределению [2, 3].

Случайным полем точек называется совокупность точек, случайным образом распределенных на плоскости. Плотностью поля точек называется среднее их число, попадающее на единицу площади.

Если плотность поля постоянна, то поле называется равномерно распределенным.

Пусть задана некоторая область Ω плоскости, a -математическое ожидание числа точек, попадающих в область Ω. Тогда вероятность P попадания m точек в область Ω равна

m

P m = — e a ,           (1)

m !

где m ! - произведение чисел от 1 до m (факториал).

Если поле точек равномерно и имеет плотность Л, то a = Л-S,(2)

где S – площадь области Ω.

Если поле не равномерно, то а = й Л( x ’ У) dxdy,

О где Л( x, у) - плотность распределения.

Дисперсия

D^ = M^ - (M^)2 = У m2 a-e-а - а2 = m=0

Математическое ожидание случайной величины

Рассмотрим равномерное пуассоновское распределение на плоскости с плотностью Л = 100 шт/м².

Пусть Ω представляет собой квадрат со стороной 1 м. Область Ω покроем равномерной сеткой с шагом 0,1 м. Тогда эта область разобьется на 100 одинаковых квадратов со стороной 10 см.

Если распределение равномерное, то в каждый из этих квадратов должно в среднем попасть по 1 точке.

Пронумеровав квадраты и подсчитав число точек в каждом из них, получим случайную величину ξ , i = 1, 2…100.

Эта случайная величина должна иметь равномерное пуассоновское распределение с параметром а = 100 • 0,01=1.

Математическое ожидание случайной величины

-х      mm                 ж      mtn -1

M E = У m —e -^а = ае^а У — ---= а . (4)

fam !              ( m - 1)!

ж

У m=2

m ( m - 1) O m - а m !

^ ma-

+ У-- e m = 0 ^m !

= a + a — a = a .

Проведем вокруг некоторой точки поля круг радиуса r . Для того чтобы расстояние R от этой точки до ближайшей к ней соседней точки было меньшее, чем r , необходимо, чтобы в круг радиуса r попала хотя бы одна точка, кроме данной.

Вероятность этого события равна

Известно, что F (r ) = 1 - e

-n r ² Л

-m

F ( r ) = У —ее e' m = 1 - !

Случайную величину R (расстояние от точки поля до ближайшей соседней) называют распределением Релея [4].

Плотность распределения Релея задается формулой f (r) = 2пЛre-nr2Л.           (7)

где a = Л - n r ² .

Математическое ожидание распределения Релея жж

M (R) = \rf (r) dr = 2пЛ[ r2 en 2Л; dr =   - = 50 мм.(8)

J0                  о

Дисперсия

ж

D(R) = M(R2) - (M(R))2 =|r2 f (r)dr - о

4 л

=« 68,47 мм ² .

В случае, когда Л = 100 шт/м², M ( R ) = 50,0 мм, D ( R ) = 68,47 мм² .

Результаты исследования. Полученные числовые характеристики равномерного пуассоновского распределения позволяют сравнивать их с рассчитанными по описанной выше методике эмпириче- скими распределениями для различных вариантов формы распределяющей поверхности. Лучшим распределением будет то, для которого усредненное минимальное расстояние между семенами будет наибольшим.

В нашем случае вместо рассматриваемых точек можно принять семена сельскохозяйственных культур.

Помимо распределения семян по квадратам математического ожидания, минимального расстояния до ближайшего соседа важной характеристикой распределения семян по площади является равномерность распределения семян по профилю, т. е. в направлении, перпендикулярном направлению движения. Можно сказать, что это распределение является проекцией двумерного распределения ( P i , P i ) на ось x . Очевидно, что лучшим распределением нужно считать то, для которого распределение по профилю будет ближе к равномерному.

Для оценки распределения по профилю разобьем раствор лапы по оси x на 10 равных интервалов слева и справа.

Так как ширина раствора лапы равна 220 мм, то длина интервала будет равна 11 мм.

С помощью программы на языке DELPHI 6.0 проведены расчеты по определению оптимальных параметров распределителя семян.

Для удобства проводимых расчетов были приняты постоянными для всех вариантов следующие величины: норма высева N_e = 1 млн на 1 га (или Л = 100 шт/м²), скорость движения сошника V = 1,11–1,94 м/с, средняя скорость движения семян в семяпроводе V = 1,53 м/с, ширина сошника В = 220 мм, угол наклона семяпровода ^ = -14°, внутренний размер семяпровода – прямоугольник со сторонами 20 и 40 мм, длина распределителя L =40 мм.

Варьируемыми параметрами распределителя принимались: координаты точек, описывающие поверхность распределителя A = ( A , A_z ), В = ( В_х , B_z ),... , J = ( J_x, J_z )   и его размеры

(ширину U , высоту H ), количество отверстий (прорезей) С , а также высота постановки распределителя над уровнем почвы P .

Меняя конструктивные параметры распределителя, определяли минимальные расстояния между семенами, а также фиксацию распределения семян по профилю (вдоль оси x ) [5].

Анализ результатов проведенных расчетов показывает, что при высоте установки распределителя P = 13 мм и при заданных численных значениях координат точек, описывающих поверхность распределителя:

A (0,26), В (1,25), С (3,24), D(6, 23),

E (7,22), F (9,20), G (17,17), H (19,16), I (31,14), J (38,13), достигается требуемая ширина рассева семян и равномерное их распределение. Вместе с тем при увеличении высоты установки распределителя свыше 15 мм наблюдается нарастание количества соударений движущихся в свободном полете семян о свод подсошникового пространства, а это влечет за собой возрастание соударений семян между собой.

Поэтому в дальнейших вычислениях величина высоты установки распределителя принималась равной не более 15 мм.

На равномерное распределение семян по ширине подсошникового пространства будет влиять не только форма и размеры распределяющего устройства, но и количество отверстий (прорезей), предназначенных для засева пространства под распределителем. Для выяснения оптимальных размеров и количества отверстий были проведены расчеты.

На основании проведенных теоретических расчетов более оптимальным оказался вариант с 5 отверстиями, одно отверстие на участке ( - B ; В ) с 50 % вырезаемой площади, два отверстия на участках ( F ; G ) и ( - F ; - G ) с 50 % вырезаемой площади, два отверстия на участках ( H ; I ) , ( - H ; - 1 ) с 50 % вырезаемой площади, причем верхняя часть прорези выполнена вогнутой, а нижняя – выпуклой.

На рисунке 4 представлена диаграмма, характеризующая зависимость среднего минимального расстояния между семенами R min от ширины U , высоты H распределителя при количестве отверстий на его поверхности С =5.

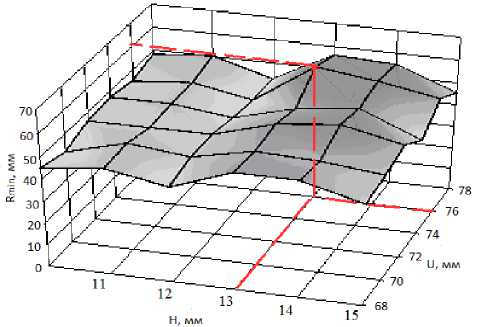
Рис. 4. Поверхность отклика, характеризующая изменение среднего минимального расстояния между семенами R min от U и H

Пики поверхности отклика на диаграмме указывают области, которым соответствуют значения рациональных параметров. На рисунке 5 показаны результаты теоретических расчетов ширины рассева семян в зависимости от скорости движения агрегата V и высоты установки распределителя над уровнем почвы P .

Таким образом, можно сделать вывод, что оптимальные характеристики равномерности распределения семян по площади обеспечивает распределитель с координатами точек, описывающих форму и размеры распределителя:

A (0,26), В (1,25), С (3,24), D (6,23),

E (7,22), F (9,20), G (17,17),

H (19,16), I (31,14), J (38,13) , - для которого U = 76 мм, H = 13 мм, L = 40 мм, количество отверстий C = 5: одно отверстие на участке ( - B ; В ) с 50 % вырезаемой площади, два отверстия на участках ( F ; G ) и ( - F ; - G ) с 50 % вырезаемой площади, два отверстия на участках ( H ; I ), ( - H ; - 1 ) с 50 % вырезаемой площади, высотой установки над уровнем почвы P = 13 мм. Максимальная ширина рассева достигается при скорости движения агрегата V =1,67 м/с.

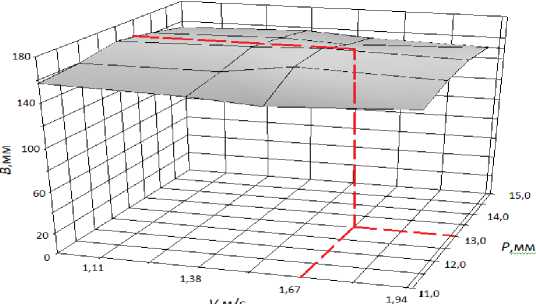
Рис. 5. Зависимость ширины рассева семян от скорости движения агрегата V и высоты установки распределителя от поверхности почвы P при U = 76 мм, H = 13 мм, С = 5

При этом достигается увеличение среднего минимального расстояния между семенами до 60,19 мм по отношению к 50,00 мм в случае теоретического пуассоновского распределения и 7,18 мм в случае использования стрельчатой лапы без распределителя.

Выводы. Проведенные теоретические исследования позволили разработать математический аппа- рат для оптимизации параметров распределителя семян. Разработанная программа для ЭВМ позволяет обоснованно определять конструктивные параметры распределительных устройств сошниковой группы для посева многолетних бобовых трав по выбранной технологии их возделывания. Рациональными значениями конструктивных параметров распределительного устройства сошника являются:

ширина U = 76 мм, высота H = 13 мм, длина L = 40 мм и количество отверстий C = 5.