Анализ рекурсивного алгоритма решения задачи о ханойской башне на основе подстановок

Задача о Ханойской башне представляет собой игру, придуманную французским математиком Франсуа Эдуардом Анатолем Люка (1842–1891) [1–3] (рис. 1).

а)                        б)

Рис. 1 . Задача о Ханойской башне: а) игрушка с восемью дисками;

• б)    ее автор Франсуа Эдуард Анатоль Люка

Азиатская тематика данной задачи, на наш взгляд, связана с тем, что в то время Вьетнам был французской колонией. Ханойская башня – задача оптимального (за кратчайшее число ходов) и своего рода безопасного (бОльший диск не может лежать на меньшем, в этом ограничении безопасность и заключается!) перемещения ("перемещения упорядоченности") с одного стержня – объекта Х на другой Z с дополнительным вспомо- гательным объектом Y (между прочим, есть задачи и не с одним Y).

Принцип разной частоты "переноса" дисков разного "диаметра" применяется в системах резервного копирования информации [4], в которых "диаметр" диска как бы соответствует периодичности копирования.

В [1] описано интересное решение задачи на соответствующем графе. Так, для двух дисков получают граф, изображенный на рис. 2.

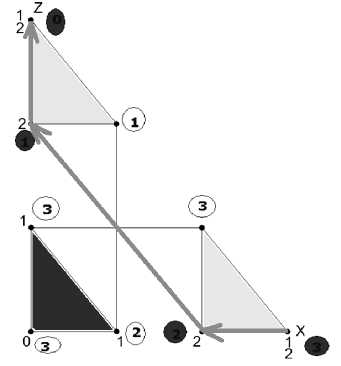
Рис. 2. Решение задачи о Ханойской башне для n=2 на графе

Имеется много подходов к алгоритмическому решению задачи [5–7]. Так, при четном числе дисков в графе всегда надо двигаться "налево", при нечетном – "направо". Можно стержни расположить в виде треугольника, тогда в нем можно двигаться по и против часовой стрелки, что использует соответствующий алгоритм.

Особый интерес представляет рекурсивный алгоритм [8]. На математических форумах пишут: "Рекурсивное решение напоминает волшебный фокус – не зная решения, а зная только некоторую закономерность задачи, получаем само решение. Фактически указывается не сама последовательность перемещений дисков, а алгоритм сведения задачи к более простому случаю" [3]. Вызывает интерес исследование деталей этого "фокуса" с методической целью, при использовании интерпретации вызовов рекурсивной процедуры в виде соответствующих подстановок.

1. Представление рекурсии системой подстановок

Рекурсивная процедура, например, может иметь вид [8]:

CARRY(n,x,z,y) – перенос дисков с х на z, используя y.

Разбиваем CARRY(n,x,z,y) на две основных подзадачи:

• 1.    CARRY(n-1,x,y,z) башню n-1 (без самого большого диска) перенести с х на y, используя z;

• 2.    CARRY(1,x,z,_) перенести один нижний диск с х на z;

• 3.    CARRY(n-1,y,z,x) перенести башню n-1 перенести с y на z, пользуясь x.

Перенос одного диска выполним как нерекурсивную процедуру ONEDISC(x,z). Получаем схему алгоритма (рис. 3).

Представим программу системой подстановок следующим образом:

^   x z y ^

n ,—,—,— I;

l   x z y J

, X y z n - 1,—,—,—;

x y z x z

- -;

xz

yzx ^{n - 1,}-J ,

yzx

В выражение (1) подстановка л \ x z y n, — , — ,—  - это CARRY(n,x,z,y: integer); с l x z y J указанием изменяющегося "смысла" переменных. В числителе – как бы глобальный смысл, в знаменателе – локальный, т. е. на данном этапе. В начале – х "откуда" – исходный стержень=x, z – "куда" – целевой = z, y – "дополнительный" = y.

xyz n — 1, —, —,— - это CARRY(n-1,x,y,z); -xyz перенос подбашни n-1 с исходного на дополнительный стержень, т. е. здесь дополнительный в качестве целевого, а целевой – в качестве дополнительного.

x, - - ONEDISC(x,z); - перенос большо-xz го диска с исходного на целевой стержень.

yzx n — 1, —, —,— - это CARRY(n-1,y,z,x), пе-yzx ренос подбашни n-1 с дополнительного стержня (он теперь в качестве исходного) на целевой стержень (он в качестве дополнительного), а исходный стержень – в качестве целевого.

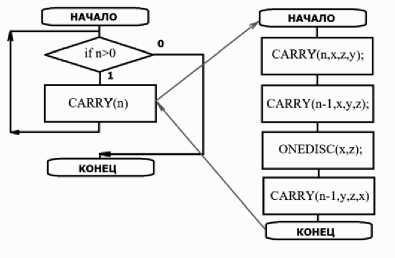
Рис. 3. Схема алгоритма решения задачи о Ханойской башне

Таким образом, при вызовах процедуры осуществляется подстановка переменных:

( x z y ^ 1 n ,—,—,— I ;		(   1 x z y ^ I n — 1,-,—,— I ;		(      x z y ^ I n — 2,-,-,— | ;
l x z y J		l     x y z J		l      x z y J
i x y z n — 1,—,—,—;		O x y z n — 2,—,—,—;		xyz n — 3,—,—,—;
x y z	■	x z y	■	xyz
x z		x z		x x.
x ’ z ’		,_; x y		,       ; xz
n — 1, y , z , x ;		n — 2, y , z , x ;		n — 3, y , z , x ;
y z x		z y x		y z x

Так, во второй "скобке" (2)

^ x X Z У У n -1, —, —, — I получается, поскольку при

V      x У z J

очередном вызове берется n — 1,—,—,— из xyz первой "скобки".

xz xz xz xz

Получаем -,-; -,—; -,-; —,—;...

xz xy xz xy

yzx

,       ,       •

zyx

(    . X Z УI n—j - -- I;

V      Z У x J

xyz ^{n —} j ^— 1, —^,_,_;

zxy

.

Это первый шаг, зависящий от четности n.

xz

,      ;

zy

xz     xz

Нечетное-- , —; четное - —, —. xz     xy

Получаем первые две подстановки:

• 1)    x,z,y,

• 2)    x,y,z и, соответственно, переносы дисков xz и xy.

Обратим еще раз внимание на чередование подстановок на этом первом проходе:

■  1 У z x n — j — 1, —, —, —;

x У z

Получаем четвертую подстановку: 4) z,y,x и перенос zy. Подстановки x,y,z, полу-

yzx

чаемые из —,—

xy

, z

yzx и x,z,y из —, —,— уже

xzy

были выше. Но получаются еще вот такие:

I( x z У | I 1(     . x z У | I 1(     „ x z У I I si n,-,-,- l^^l n —1,-,-,- l^^l n — 2,-,-,- tl^ [V x z У J J [V     x У z J J [V     x z У J J

xyz zxy

xy и —,—

yxz

z

,—, их еще не было.

Соответственно:

xyz

Подставляем —, —,—

zxy

1 x У z I f _ x у z I f „ x у z I n — 1,-,-,-; |^ n — 2-,-,-; l^S n — 3,-,-,-; !^ x У z J [       x z У J [       x У z J

, x z У I n — k,—,—,— I;

z x У J

f ₁yzx 1 f У у Z X 1 f У у Z X 1

S n — 1---; !^s n — 2,-,--; |^S n — 3,-,-,-; !^ ....

[     У z x J [      zуx J [     У z x J

Далее от них (после них) идет "переломная"

xyz n — k —1>_>_>_;

x

zy

xz

,-;

zx

! .

yzx   yzx команда либо —, —, — , либо —, — , — .

yzx   zyx

yzx

Проверим после — , —, — : yzx

fr n— V

xz i ,-,-

у \

,

У z x J

xyz

n — i — 1, —, —,-;

yxz

xz

,     ;

yz

yzx ^{n —} i ^{— 1, —,-, —;}

xzy

.

Получаем третью подстановку 3) y,z,x и перенос yz.

Проверим после

n — k — 1, ^У , —

x ,-;

У x Z

Таким образом, имеем пятую новку 5) z,x,y и перенос zx.

xyz

Подставляем —,—,— : yxz

[ n — l , ^x , -, ^У ) V      У x z J

xyz n — l —1,_,_,_;

x

yz

xz

,      ;

yx

n — l — 1, ^У , -

x

,      ;

z x У

>

подста-

Таким образом, получаем подстановку 6) y,x,z и перенос yx. Получаем все 6=3! вариантов перестановок xyz и 6 возможных переносов с одного стержня на другой.

2. Анализ подстановок переменных в рекурсивном алгоритме решения задачи о Ханойской башне при n=1

yzx

Затем идет вызов 0, —, —, — yzx

Проанализируем изменение порядка переменных для n=1. Первый вызов:

ГГ              1

1, x , -, y ;

I x ^- y J

⁰ т, 1 , У ; к ^{у z x} J

yzx

0,  ,-,-^

0, x , y , ^- ;

xyz

xz

,-;

xz

0, y , ^- , x

yzx

xyz

Далее 0, — , — , — ; вызывает снова проце-xyz дуру с другими значениями переменных:

x z у о,-,-Л ; к X у z J

—

yzx

xyz

1,     ,     ,     ;

yxz

xz

,-;

yz

1, y , ^- , x

xzy

Перестановки переменных при этом вы-

глядят следующим образом (рис. 5):

0, x , y , ^- ; 4

X y z

xyz

1,     ,     ,     ;

xzy

•

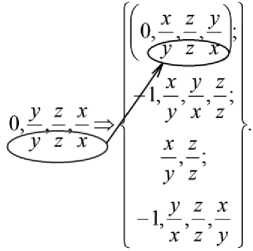
Рис. 5. Изменение порядка переменных при n=1 и вызове 0, y , ^- , x .

yzx

—

xz

,-; xy

1, y,-, x zyx

Поскольку получаем -1, то этот вызов заканчивается. Перестановки переменных при этом выглядят следующим образом (рис. 4):

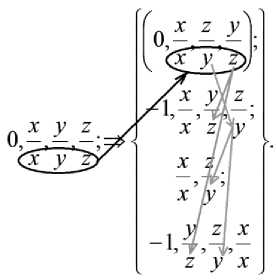
Рис. 4. Изменение порядка переменных

xyz при n=1 и вызове 0, —, —,— xyz

Далее выполняется единственный пере- xz нос (10): x,z : —, —.

xz

Поскольку и здесь получаем -1, то и этот вызов заканчивается. Конец процедуры.

Таким образом, осуществляется единст- xz венный перенос: x, - : —, —.

xz

Здесь алгоритм не доходит до переноса "подбашни", так как ее нет, переносится только самый большой диск (а у нас всего один диск, он и есть самый большой!). Всего одна (исходная) подстановка значений переменных. Дерево решения для n=1 имеет вид на рис. 6.

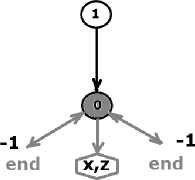
Рис. 6. Дерево решения для n=1

3. Анализ подстановок переменных в рекурсивном алгоритме решения задачи о Ханойской башне при n=2, n=3

В случае вид:

n=2 "первый

проход" имеет

<

? x z y b

2,    ,    , I;

x z У J

xyz

1,     ,     ,     ;

xyz

r^i

xz

,-;

xz

1, y, z, x

yzx

;

1 x z y b

1,     ,      , I;

x y z J

0, x, y, z;

xzy

ri

x

z

xy

0, y, z, x

zyx

;

0, x, z, y|;

x z y J

^^^^^^в

xyz

1,    ,    ,    ;

xyz

xz

,     ;

xz

^^^^в

yzx

1,_,_,_;

yzx

r.

Далее, рассуждая аналогично вышеописанному, получаем 2-1-0 (перенос 1)-1 (перенос 2)-1(перенос 3 после "перелома"). Дерево решения для n=2 изображено на рис. 7.

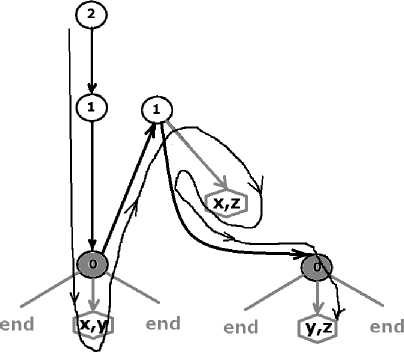
Рис. 7. Дерево решения для n=2

В случае n=3 получим (рис. 8):

, X Z У

3, ,    ,       I ;

X Z У J

7 XZ У ).

2,    ,    ,     ;

X У Z J

, x z У

1,    ,-, I ;

X Z У J

xyz

2,    ,    ,   ;

xyz xz

,     ;

xz

r^i

yzx

2,    ,   ,    ;

yzx

xyz

1,     ,     ,;

xzy xz

,;

xy yzx

1,     ,     ,;

zyx

r ^ i

0, x , ^У , ^Z ;

xyz

xz

, xz

0, ^У , ^Z , x ;

yzx

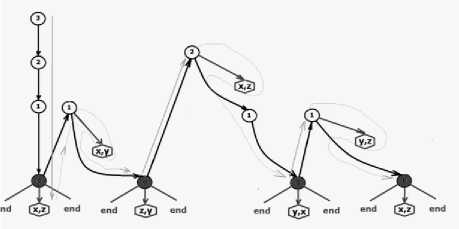
Рис. 8. Дерево решения для n=3

Выводы

Таким образом, использование формализации в виде подстановок, позволяет проанализировать изменение значений переменный при рекурсивных вызовах. Этот подход объясняет принцип выбора переноса диска в алгоритме решения задачи о Ханойской башне, что можно использовать в методических целях при проведении занятий по дисциплине "Алгоритмы и анализ сложности".