Анализ системы управления демонстратора одного типа

Актуальной задачей при разработке образцов авиационной и ракетной техники является синтез систем управления, обеспечивающих качество процессов управления такими аппаратами. К практическим задачам синтеза систем управления летательных аппаратов можно отнести:

• -    задачи выбора типа и разработки конструкций управляющей части летательных аппаратов, обеспечивающих возможность качественного управления полетом [1, 2];

• -    синтез систем стабилизации и ориентации таких аппаратов, обеспечивающих в итоге заданное качество их движения по необходимой траектории [3, 4];

• -    разработка навигационных систем, обеспечивающих получение параметров движения л е-тательного аппарата с приемлемой точностью [5, 6].

В ЮУрГУ проводятся работы по созданию демонстраторов технологий, используемых в авиационной и ракетной технике. В статье рассматриваются вопросы, связанные с реализацией системы управления демонстратора одного типа.

Схема демонстратора

Кинематическая схема демонстратора приведена на рис. 1. Количество степеней свободы подвижной части демонстратора 1 ограничено направляющими штангами 2, с которыми она связана через скользящие вдоль штанга шарнирами 3. В результате подвижная часть демонстратора может совершать поступательное движение вдоль оси 0y и вращательное движение вокруг оси, параллельной, 0z , где 0x y z – стартовая система координат.

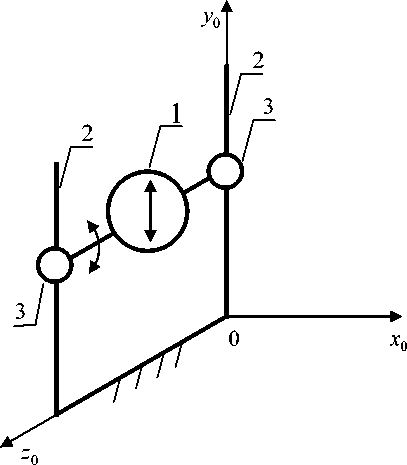
Рис. 1. Кинематическая схема демонстратора

На рис. 2 приведена схема подвижной части демонстратора. Маршевый двигатель МД создает вектор тяги P , который проходит через ось вращения подвижной части демонстратора. Центр масс демонстратора смещен относительно оси вращения на расстояние A l . Двигатели ориентации ДО имеют постоянную тягу P и P и включаются/выключаются попарно, обеспечивая возможность вращения и стабилизации подвижной части демонстратора по углу 9 .

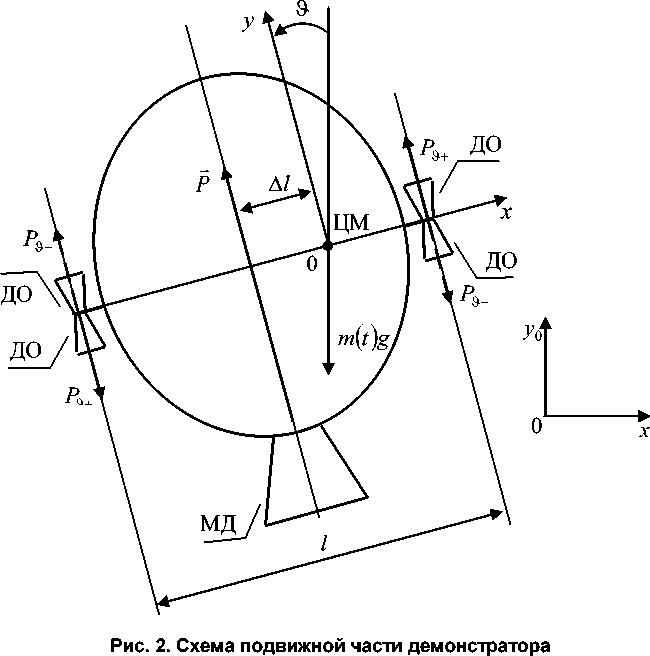
Садов В.Б., Чернецкий В.О., Алёшин Е.А.	Анализ системы управления демонстратора одного типа
Полагаем, что стартовая масса демонстратора m ( 0 ) = 121 кг,	(1)
момент инерции относительно оси вращения J z ( 0 ) = 21,58 кг - м2, смещение ЦМ относительно оси вращения находится в диапазоне	(2)
A l = ± 0,02 м, суммарное плечо сил ДО	(3)
l = 1 м.	(4)

Предполагается, что все двигатели будут работать на смеси спирт + жидкий кислород. Примем, что величина удельного импульса в этом случае

I_y= 3 3100 м/с.                                                                          (5)

Канал управления вертикальным перемещением

Если пренебречь силами трения в шарнирах 3, двигающихся вдоль направляющих штанг 2 (см. рис. 1), то в соответствии с рис. 2 уравнение движения вдоль оси 0 y будет иметь вид

У = Дх P cos d- g , m ( t )

где у - перемещение вдоль оси 0 y ₀; P - сила тяги МД; m ( t ) - масса подвижной части демонстратора в текущий момент времени; 9 - угол поворота подвижной части демонстратора; g - ускорение силы земного притяжения (действует только при у >  0 , поскольку до момента старта и после приземления сила земного притяжения уравновешивается силой реакции опоры).

Примем, что сила тяги МД

P = P + AP = m (0)g + AP,

где P – постоянная составляющая силы тяги, необходимая для уравновешивания силы земного притяжения в момент старта; AP - переменная составляющая силы тяги, необходимая для управления движением вдоль оси 0 y .

Будем считать, что величина A P лежит в диапазоне

AP = ±0,1 P0.                                                                                 (8)

Текущее значение m ( t ) может вычисляться по формуле

t

m (t) = m (0)-j(m мд (t) + ma(t ))dt,

0

где m_M({t ) - текущий секундный массовый расход МД; m_a(t ) - текущий суммарный секундный массовый расход ДО.

Для измерения параметров движения используем данные бесплатформенной инерциальной навигационной системы (БИНС) [7]. При предварительном анализе системы управления демонстратором будем считать, что БИНС работает идеально, т. е. обеспечивает точное измерение всех необходимых величин и не вносит в контур управления никаких задержек.

В результате структурная схема канала управления вертикальным перемещением будет иметь вид, приведенный на рис. 3, где МД – структурная схема модели МД; Py – структурная схема регулятора канала вертикального перемещения; yпр – программное значение перемеще- ния; у и у - текущие значения перемещения и его производной; mi‘Р - программное значение секундного массового расхода МД.

9              ^- g

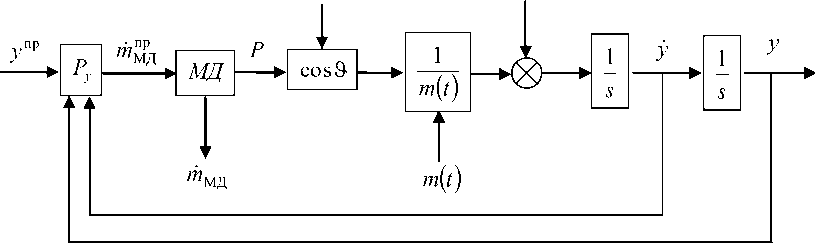
Рис. 3. Структурная схема канала вертикального перемещения

Будем полагать, что модель МД имеет вид, приведенный на рис. 4, где T , T и T , T – соответственно постоянные времени дроссельного регулятора расхода и камеры сгорания.

Рис. 4. Структурная схема модели МД

Синтез регулятора P может осуществляться различными способами, используя как требуемые прямые показатели качества регулирования, так и передаточные функции и частотные методы. Этой теме посвящено достаточно большое количество как учебных и научных книг [8, 9, 10], так и статей по синтезу регуляторов различного вида [11, 12, 13].

В качестве регулятора P будем использовать регулятор, построенный по схеме подчиненно

,               m (0)g                             „                                          „ го регулирования (рис. 5), где       – величина постоянной части массового расхода МД, необ-

Iуд ходимой для компенсации силы земного притяжения (в момент старта). Данные типы регуляторов достаточно часто применяются в приводной технике [14]. Исходя из (7), (8), уровень ограничения переменной составляющей массового расхода c может быть вычислен как c = 0,1 тЖ

I уд

.

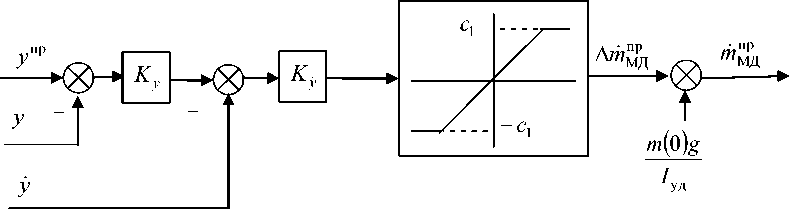
Рис. 5. Структурная схема регулятора P канала вертикального перемещения

Канал управления углом поворота

Исходя из рис. 2, уравнение вращательного движения будет иметь вид

S =    IM, + Mz ), где создаваемый ДО момент

Mz = Mz +- Mz -,(12)

Mz + = P»^ + Al ] + PS. | — Al) = P.1,(13)

Mz - = P»-1.(14)

Обусловленный смещением ЦМ относительно оси вращения возмущающий момент определяется выражением

Mz =- m (t) gAl cosS.(15)

Будем считать, что момент инерции в текущий момент времени в первом приближении пропорционален массе подвижной части демонстратора, т. е.

J (t)~ J70 m(t).

m ( 0 )

В результате структурная схема канала управления углом поворота будет иметь вид, представленный на рис. 6, где P - регулятор; ДО - структурная схема модели блоков ДО; m ПР и /й Пр - суммарные массовые расходы пар ДО, обеспечивающих моменты M_z+ и M_z _; »^пр - программное значение угла поворота; S и S - текущие значения угла поворота и его производной.

M в     m ( t )

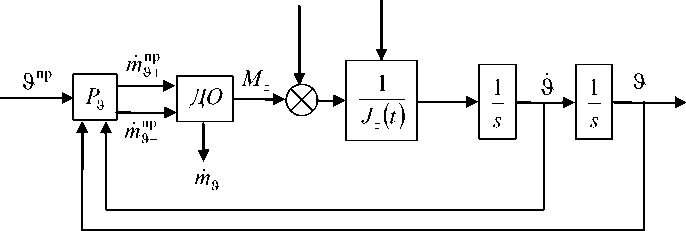
Рис. 6. Структурная схема канала управления углом поворота

Будем считать, что структурная схема модели блоков ДО имеет вид рис. 7, где T ₅ , T ₆ и T ₇ , T – соответственно постоянные времени клапанов и камер сгорания (по аналогии со структурной схемой МД, представленной на рис. 3).

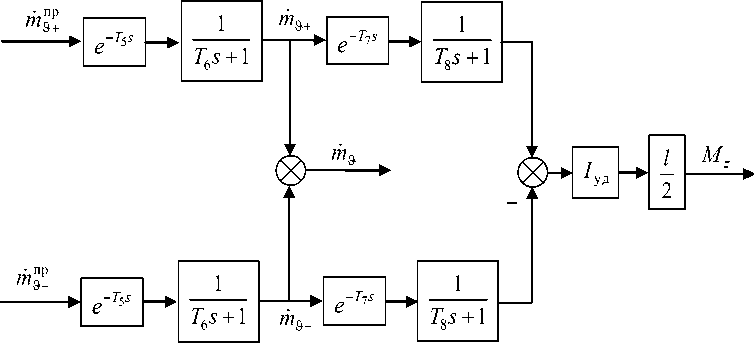
Рис. 7. Структурная схема модели блоков ДО

Для того, чтобы возмущающий момент M® не приводил к появлению статической ошибки, регулятор р должен быть астатическим. Будем использовать регулятор, построенный по схеме подчиненного регулирования в соответствии со структурной схемой, показанной на рис. 8. Элементы подобных регуляторов с двухпозиционным реле приведены в [15, 16, 17].

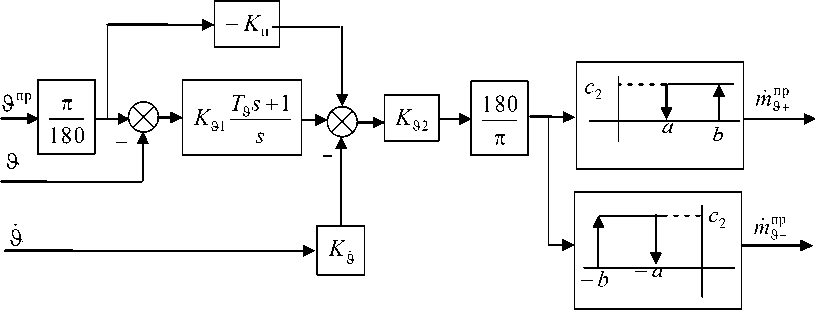
Рис. 8. Структурная схема регулятора P канала управления углом поворота

Параметр с2 релейных элементов регулятора должен иметь значение c = 2р+= 2 р9

.

I уд       I уд

Блоки с коэффициентами ^^ и

--- используются для того, чтобы программное значение

п угла 3пр, а также пороги а и b срабатывания релейных элементов задавать в градусах. Блок с коэффициентом - Ки обеспечивает инвариантную связь, уменьшающую перерегулирование, вызываемое наличием нуля в передаточной функции ПИ-регулятора К91 35 + ' .

s

Результаты моделирования

Поскольку при А / = ± 0,02 м максимальное значение возмущающего момента, исходя из (15), составляет M® = m ( о ) g А / ® +23,7 Н-м, для возможности компенсации данного момента необходимо, чтобы ДО обеспечивали управляющие моменты M_{z +} = M_z _ > | м ® |. Поэтому в качестве их значений было принято M_{z +} = M_z_ = 35 Н - м. В результате, исходя из (13), (14), каждый из четырех ДО должен обеспечивать тягу р₊ = р_ = 35 Н. В качестве параметров модели ДО (рис. 7) были приняты значения T = T ₆ = T = Т ₈ = 0,02 с.

Настройка регулятора (рис. 8) канала управления углом поворота выполнялась на автономной его модели без учета изменения момента инерции в процессе выгорания топлива и при нулевом значении возмущающего момента M ^в . При этом использовалась общеизвестная методика настройки контуров систем подчиненного регулирования. В результате были получены следующие параметры регулятора: К _{3 1} = 1; К _{3 2} = 5; К ₉ = 0,3; К _и = 0,6; T = 1; а = 1 ; b = 2 . Величина параметра c настройке не подлежит и определяется выражением (17).

В качестве параметров модели МД (см. рис. 4) первоначально были приняты значения T = T 2 = T₃ = T 4 = 0,1 с. В результате настройки были получены следующие параметры регулятора (см. рис. 5) канала управления вертикальным перемещением: К = 0,6 ; К ^ = 0,06. Величина параметра с 1 настройке не подлежит и определяется выражением (10).

Дальнейшее моделирование осуществлялось для совместной работы каналов с учетом изменения массы и момента инерции в процессе выгорания топлива.

Моделирование производилось с использованием пакета Matlab и его компонентов Simulink [18, 19].

Результаты моделирования отработки задания по высоте при первоначально принятых параметрах модели МД приведены на рис. 9.

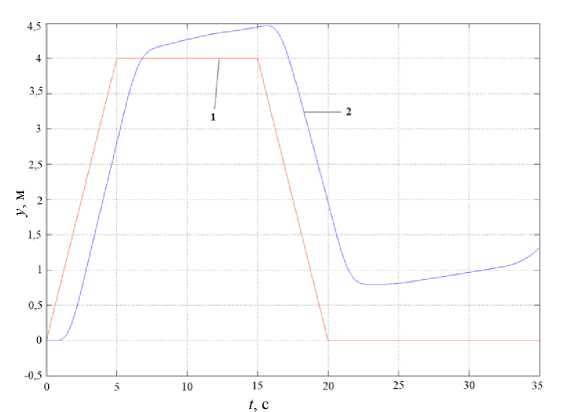
Рис. 9. Отработка задания по вертикальному перемещению при параметрах МД Т 1 = Т 2 = Т 3 = Т 4 = 0,1 с; 1 – задание, 2 – отработка

Как видно из рис. 9, работу канала управления вертикальным перемещением нельзя признать удовлетворительной. Это происходит из-за того, что при таких больших значениях постоянных времени модели МД система просто не успевает отрабатывать возмущение, вызванное уменьшением массы подвижной части демонстратора при выгорании топлива.

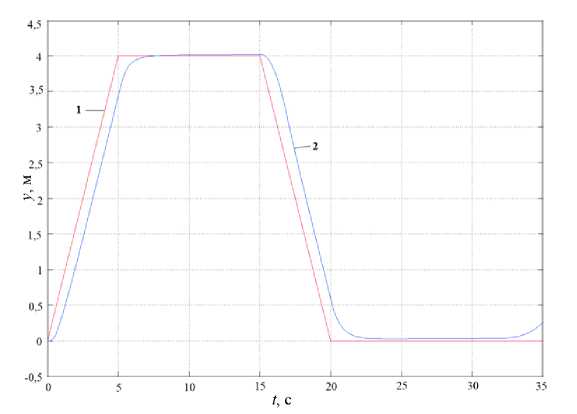
Если принять постоянные времени модели МД равными T_x = T ₂ = T = T = 0,02 с, то результаты отработки задания по высоте будут иметь вид, представленный на рис. 10.

3.5

2.5 S

^■2

0.5

15           20

t , с

Рис. 10. Отработка задания по вертикальному перемещению при параметрах МД Т 1 = Т 2 = Т 3 = Т 4 = 0,02 с; 1 – задание, 2 – отработка

Из рис. 10 видно, что при данных параметрах МД канал управления вертикальным перемещением работает удовлетворительно на протяжении примерно 30 с. В дальнейшем работа канала становится невозможной, поскольку ограничение на изменение тяги МД не позволяет скомпенсировать уменьшение массы подвижной части демонстратора.

На рис. 11–13 представлены результаты моделирования канала управления углом поворота при различных величинах смещения A l ЦМ от оси вращения.

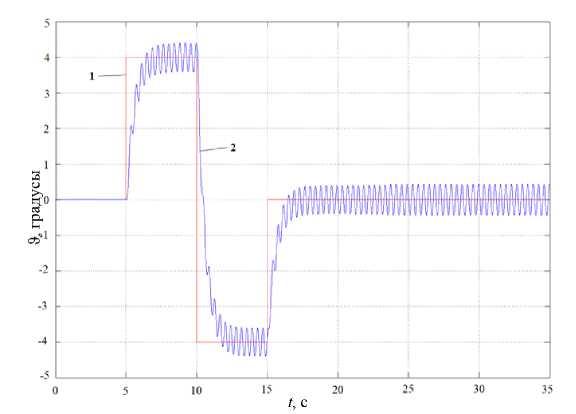
Рис. 11. Отработка задания по углу поворота при A l = 0 ; 1 - задание, 2 - отработка

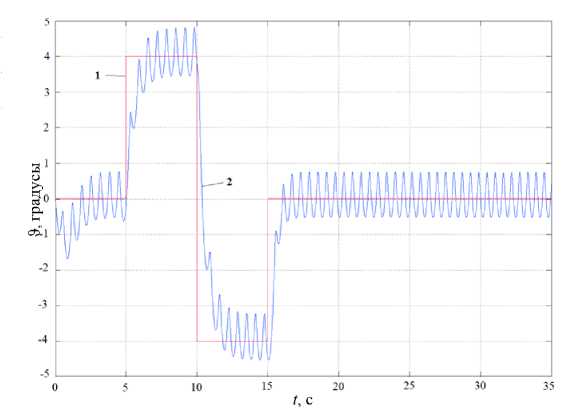
Рис. 12. Отработка задания по углу поворота при Al = 0,02 м; 1 - задание, 2 - отработка

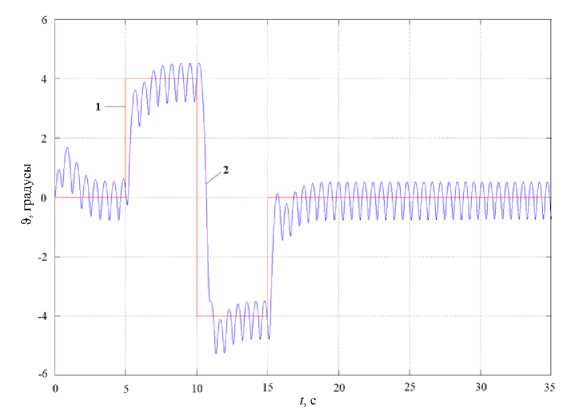
Рис. 13. Отработка задания по углу поворота при A l = - 0,02 м; 1 - задание, 2 - отработка

Как видно из рис. 11–13, в канале управления углом поворота возбуждаются автоколебания. Их амплитуда тем больше, а частота тем меньше, чем больше величина абсолютного отклонения ЦМ от оси вращения. Такое изменение амплитуды и частоты обусловлено тем, что часть создаваемого ДО момента расходуется на компенсацию возмущающего момента от смещения ЦМ.

Анализ влияния характеристик БИНС на характеристики системы

При моделировании движения демонстратора необходимо учитывать работу навигационной системы. Например, в схеме на рис. 6 углы 9 и скорости 9 выдаются навигационной системой со своими статическими и динамическими погрешностями.

Рассмотрим погрешности позиционирования демонстратора, обусловленные дрейфами и статическими погрешностями определения углов поворота демонстратора. Будем использовать встроенные датчики электронного гироскопа платы STM32F411-DISCO [20, 21]. Замер дрейфа датчика скорости гироскопа (I3G4250D) дал нам значение примерно ϑ = 1,77 ⋅ 10 ^{- 5} (градусов/c)/c. Двойное интегрирование этой величины по времени даст нам среднее текущее отклонение угла от нулевого положения, то есть ϑ ( t ) = ∫ ∫ (1,77 ⋅ 10 ^{- 5} ⋅ dt ) ⋅ dt = 1,77 ⋅ 10 ^{- 5} ⋅ t ² /2 в градусах. При этом появляется боковая сила за счет появившейся проекции тяги. Считая силу тяги примерно равной весу подвижной части демонстратора, можно записать

F _бок = m ⋅ g ⋅sin(ϑ)≈ m ⋅ g ⋅ϑ. (18)

Отсюда текущее значение бокового ускорения определяется как a _бок ≈ g ⋅ϑ.

Боковое перемещение за время полета 15с за счет дрейфа датчика скорости можно найти как

15 t                                           -54

S=g⋅∫∫(ϑ(t)⋅dt)⋅dt=9,81⋅1,77⋅10

0 0

= 0,0064 м.

Это перемещение является незначительной величиной и не требует коррекции горизонтального положения демонстратора при свободном его движении.

Рассмотрим смещение демонстратора за счет ошибок определения углового положения датчиков. Датчик у нас выдает скорость в диапазоне ±245 градус/с. Погрешность установки общего коэффициента усиления по скорости некалиброванного датчика составляет до ± 37 градус/с. (15– 17 %).Тогда при поддержании углового положения, например в 2 градуса, боковое перемещение за счет погрешности датчика (по аналогии с предыдущим расчетом) при отсутствии смещения его нулевого положения может составить

² _{S = 9,81 ⋅} 2 ⋅ 0,17 ⋅ t 2 ⋅ 57

= 0,67 м.                                                                 (21)

Эта величина может являться существенной и будет требовать в первую очередь тарировки датчика угловой скорости с целью определения коэффициента скорость поворота – выходной сигнал датчика. Но для этого необходимо иметь соответствующий стенд, позволяющий обеспечивать необходимые углы и скорости поворота БИНС с высокой точностью.

Выводы

• 1.    Поскольку при импульсном управлении углом поворота подвижной части демонстратора в системе управления неизбежны автоколебания, конструкция демонстратора будет испытывать периодические ударные нагрузки, обусловленные периодическим включением/выключением ДО.

• 2.    Измерительная система (БИНС) должна отслеживать автоколебания в канале управления углом поворота без существенных амплитудных и фазовых искажений, т. е. иметь повышенную (по сравнению с непрерывным управлением) полосу пропускания и частоту дискретизации.

• 3.    Для разработки регуляторов каналов системы управления необходимо:

• а)    получить достоверные модели и их параметры для МД и ДО как элементов системы управления;

• б)    разработать и изготовить БИНС и получить ее динамическую модель и параметры как элемента системы управления (включая исследования ее работы на стенде, имитирующем движение корпуса демонстратора);

• в)    определить или оценить параметры упругих колебаний элементов конструкции.

• 1.    Уманский, С. Ракеты-носители. Космодромы / С. Уманский. – М.: Рестарт, 2001. – 216 с.

• 2.    Гущин, В.Н. Основы устройства космических аппаратов / В.Н. Гущин. – М.: Машиностроение, 2003. – 272 с.

• 3.    Айзенберг, Я.Е. Проектирование систем стабилизации носителей космических аппаратов / Я.Е. Айзенберг, В.Г. Сухоребрый. – М.: Машиностроение, 1986. – 224 с.

• 4.    Кузовков, Н.Т. Системы стабилизации летательных аппаратов / Н.Т. Кузовков. – М.: Высшая школа, 1975. – 304 с.

• 5.    Лысенко, Л.Н. Наведение и навигация баллистических ракет / Л.Н. Лысенко. – М.: Изд-во МГТУ им. Н.Э.Баумана, 2007. – 672 с.

• 6.    Шалыгин, А.С. Навигация и наведение космических аппаратов / А.С. Шалыгин, В.А. Санников, И.Л. Петрова. – СПб.: Балт. гос. техн. ун-т, 2008. – 143 с.

• 7.    Матвеев, В.В. Основы построения бесплатформенных инерциальных навигационных систем / В.В. Матвеев, В.Я. Распопов. – СПб.: ГНЦ РФ ОАО «Концерн «ЦНИИ «Электроприбор», 2009. – 280 с.

• 8.    Ким, Д.П. Теория автоматического управления. Т.1. Линейные системы / Д.П. Ким. – М.: Физматлит, 2003. – 288 с.

• 9.    Мирошник, И.В. Теория автоматического управления. Линейные системы / И.В. Мирош-ник. – СПб.: Питер, 2005. – 336 с.

• 10.    Ерофеев, А.А. Теория автоматического управления / А.А. Ерофеев. – СПб.: Политехника, 2003. – 302 с.

• 11.    Анучин, А.С. Система подчиненного регулирования с параллельной коррекцией по напряжению выхода понижающего преобразователя постоянного тока / А.С. Анучин, Е.О. Столяров, Д.М. Шпак и др. // Известия СПбГЭТУ «ЛЭТИ» № 7/2020. – С. 87–94.

• 12.    Тютиков, В.В. Подчиненное регулирование координат электромеханических систем на базе метода АКАР / В.В. Тютиков, А.И. Воронин // Известия ЮФУ, технические науки №5(106)/2010. – С. 155–164.

• 13.    Шилов, К.Е. Разработка системы автоматического управления беспилотным летательным аппаратом мультироторного типа / К.Е. Шилов // Труды МФТИ. – 2014. – Т. 6, № 4. – С. 139–152.

• 14.    Анучин, А.С. Системы управления электроприводов / А.С. Анучин. – М.: Академия, 2015. – 372 с.

• 15.    Разыграев, А.П. Основы управления полетом космических аппаратов: учеб. пособие для вузов / А.П. Разыграев. – М.: Машиностроение, 1990. – 480 с.

• 16.    Васильев, В.Н. Системы ориентации космических аппаратов. М.: ФГУП «НПП ВНИИЭМ», 2009. – 310 с.

• 17.    Алексеев К.Б., Бебеин Г.Г. Управление космическими летательными аппаратами / К.Б. Алексеев. – М.: Машиностроение, 1974. – 340 с.

• 18.    Дьяконо, В. MATLAB 6: учебный курс / В. Дьяконо. – СПб.: Питер, 2001. – 592 с.

• 19.    Система моделирования динамических систем Simulink [Электронный ресурс]. URL: http://bourabai.ru/cm/simulink.htm (дата обращения 5.05.2021). – Текст: электронный.

• 20.    Инструкция пользователя конструктора 32F411EDISCOVER .– URL: https://www.st.com/content/ccc/resource/technical/document/user_manual/e9/d2/00/5e/15/46/44/0e/DM 00148985.pdf/files/DM00148985.pdf/jcr:content/translations/en.DM00148985.pdf (дата обращения 5.04.2021). – Текст: электронный.

• 21.    Инструкция пользователя I3G4250D: MEMS датчик движения: 3-степенной цифровой гироскоп [Электронный ресурс]. URL: https://www.st.com/resource/en/datasheet/i3g4250d.pdf (дата обращения 5.05.2021). – Текст: электронный.

ANALYSIS OF THE CONTROL SYSTEMOF A DEMONSTRATION OF ONE TYPE

V.B. Sadov, sadovvb@susu.ruV.O. Chernetsky, chernetckiivo@susu.ruE.A. Alyoshin, aleshinea@susu.ru

South Ural State University, Chelyabinsk, Russian Federation

• 1.    Umanskiy S. Rakety-nositeli. Kosmodromy [Launch vehicles. Spaceports]. Moscow, Restart, 2001. 216 p.

• 2.    Gushchin V.N. Osnovy ustroystva kosmicheskikh apparatov [Fundamentals of spacecraft design]. Moscow, Mashinostroenie, 2003. 272 p.

• 3.    Ayzenberg Ya.E., Sukhorebryy V.G. Proektirovanie sistem stabilizatsii nositeley kosmicheskikh apparatov [Design of stabilization systems for spacecraft carriers]. Moscow, Mashinostroenie, 1986. 224 p.

• 4.    Kuzovkov N.T. Sistemy stabilizatsii letatel'nykh apparatov [Aircraft stabilization systems]. Moscow, Vysshaya shkola, 1975. 304 p.

• 5.    Lysenko L.N. Navedenie i navigatsiya ballisticheskikh raket [Guidance and navigation of ballistic missiles]. Moscow, MGTU im. N.E.Baumana Publ, 2007. 672 p.

• 6.    Shalygin A.S., Sannikov V.A., Petrova I.L. Navigatsiya i navedenie kosmicheskikh apparatov [Navigation and guidance of spacecraft]. Sankt-Peterburg, Balt. gos. tekhn. un-t, 2008. 43 p.

• 7.    Matveev V.V., Raspopov V.Ya. Osnovy postroeniya besplatformennykh inertsial'nykh navigatsionnykh sistem [Basics of building strapdown inertial navigation systems]. Sankt-Peterburg, GNTs RF OAO «Kontsern «TsNII «Elektropribor», 2009. 280 p.

• 8.    Kim D.P. Teoriya avtomaticheskogo upravleniya. T.1. Lineynye sistemy [Theory of automatic control. T.1. Linear systems]. Moscow, Fizmatlit, 2003. 288 p.

• 9.    Miroshnik I.V. Teoriya avtomaticheskogo upravleniya. Lineynye sistemy [Theory of automatic control. T.1. Linear systems]. Sankt-Peterburg, Piter, 2005. 336 p.

• 10.    Erofeev A.A. Teoriya avtomaticheskogo upravleniya [Theory of automatic control]. Sankt-Peterburg, Politekhnika, 2003. 302 p.

• 11.    Anuchin A.S., Stolyarov E.O., Shpak D.M., Surnin D.K. [Slave Control System with Parallel Voltage Correction of DC-buck Converter Output]. Proceedings of Saint Petersburg Electrotechnical University, 2020, no 7, pp. 87–94. (in Russ).

• 12.    Tyutikov V.V. [Slave regulation of the coordinates of electromechanical systems based on the ACAR method]. Izvestiya SFedU. Engineering sciences , 2010, no. 5(106), pp. 155–164. (in Russ)

• 13.    Shilov K.E. Razrabotka sistemy avtomaticheskogo upravleniya bespilotnym letatel'nym apparatom mul'tirotornogo tipa [Development of an automatic control system for an unmanned aerial vehicle of a multi-rotor type]. Proceedings MFTI , 2014, vol. 6, no 4. pp. 139–152. (in Russ).

• 14.    Anuchin A.S. Sistemy upravleniya elektroprivodov [Electric drive control systems]. Moscow, Akademiya, 2015. 372p.

• 15.    Razygraev A.P. Osnovy upravleniya poletom kosmicheskikh apparatov: Ucheb. posobie dlya vtuzov [Fundamentals of spacecraft flight control: Proc. allowance for universities]. Moscow, Mashinostroenie, 1990. 480 p.

• 16.    Vasil'ev V. N. Sistemy orientatsii kosmicheskikh apparatov [Spacecraft orientation systems]. Moscow, FGUP “NPP VNIIEM”, 2009. 310 p.

• 17.    Alekseev K.B. Upravlenie kosmicheskimi letatel'nymi apparatami [Spacecraft control]. Moscow, Mashinostroenie, 1974. 340 p.

• 18.    D'yakonov V. MATLAB 6: Uchebnyy kurs [MATLAB 6: Tutorial]. Sankt-Peterburg, Piter, 2001. 592 p.

• 19.    Sistema modelirovaniya dinamicheskikh sistem Simulink . [Simulink Dynamic Systems Modeling System] Available at: http://bourabai.ru/cm/simulink.htm (accessed 5.05.2021).

• 20.    Instruktsiya pol'zovatelya konstruktora 32F411EDISCOVERY . [User's manual for constructor 32F411EDISCOVERY] Available at: https://www.st.com/content/ccc/resource/technical/document/ user_manual/e9/d2/00/5e/15/46/44/0e/DM00148985.pdf/files/DM00148985.pdf/jcr:content/translations/ en.DM00148985.pdf (accessed 5.04.2021).

• 21.    Instruktsiya pol'zovatelya I3G4250D: MEMS datchik dvizheniya: 3-stepennoy tsifrovoy giroskop . [User manual I3G4250D: MEMS motion sensor: 3-degree digital gyroscope] Available at: https://www.st.com/resource/en/datasheet/i3g4250d.pdf (accessed 5.05.2021).

ОБРАЗЕЦ ЦИТИРОВАНИЯ