Анализ случайных процессов со стационарными приращениями на примере чисел Вольфа

Случайные процессы со стационарными приращениями были введены А.Н. Колмогоровым [1]. Очевидно, что любой стационарный случайный процесс является одновременно и процессом со стационарными приращениями. В то же время, существуют и нестационарные процессы со стационарными приращениями. Простейшие примеры таких процессов - это линейные функции, и(г) = с 1 г + с₀, где с₀ и с , - постоянные.

Медленные изменения скоростей будут мало сказываться на значениях их приращений Ди(г) = и(г 1 ) — и(г₂). При переходе от скоростей и(г) к разностям Ди(г) компоненты процесса с большими периодами подавляются, и приращения скоростей оказываются стационарными, зависящими только от расстояния между точками, в которых измеряются скорости Дг = г 1 — г₂. Случайную функцию и(г) называют случайной функцией со стационарными приращениями.

Для процессов со стационарными вторыми приращениями случайная функция и(г) будет полиномом второй степени и т.д.

Инструментом описания случайных процессов со стационарными приращениями служат структурные функции. В ста- тье, посвященной исследованию турбулентности, А.Н. Колмогоров вводит структурную функцию как математическое ожидание квадрата разности мгновенных значений скоростей, измеренных в соседних точках случайного поля скоростей.

В теории случайных процессов со стационарными приращениями структурная функция также важна, как и корреляционная функция для теории стационарных процессов.

Настоящая статья является первой в цикле публикаций, посвященных исследованию случайных процессов со стационарными приращениями и структурных функций Колмогорова. Анализ проводится на примере одного из показателей солнечной активности, который представлен числами Вольфа w(t). Рассматривается временной ряд ежедневных данных в период с 30.10.1913 по 31.10.2022. Далее будет показано, что в этот период динамика чисел Вольфа определяет случайный процесс со стационарными приращениями, Дw(t) = w(t₂) — w(t 1 ), стационарность понимается в узком смысле. На разных временных интервалах вероятностное распределение приращений чисел Вольфа остается инвариантным и следует логистическому закону.

В последующих публикациях будут рассмотрены результаты анализа структурных функций для чисел Вольфа, связанные с диапазонами простой и расширенной масштабной инвариантности, зависимости показателей аллометрии от порядка структурных функций, а также взаимосвязи между локальными минимумами структурных функций и границами диапазонов автомодельности.

Числовой показатель солнечной активности

С активной областью на Солнце связаны многие явления: пятна, факелы, факельные поля, сильные магнитные поля, корональные конденсации, усиленное радиоизлучение, источники ультрафиолетового и рентгеновского излучения, области вспышек. Одни области активнее других, однако не существует единственного признака, по которому можно было бы охарактеризовать активную область Солнца. Основными мерами активности являются площади пятен, числа пятен, размеры и интенсивности факелов и факельных по- лей, потоки рентгеновского, ультрафиолетового и радиоизлучения.

Наиболее известное явление – это солнечные пятна, области с сильным магнитным полем и пониженной температурой [2]. Количество солнечных пятен или чисел Вольфа определяют как:

w = k(f + 10g),            (1)

где: / - количество наблюдаемых пятен;

g - количество наблюдаемых групп пятен;

к - нормировочный коэффициент.

В качестве объекта дальнейшего анализа рассматривается ежедневная динамика чисел Вольфа.

Стационарный характер приращений чисел Вольфа.

На рисунке 1 изображена ежедневная динамика чисел Вольфа с 30.10.1913 по 31.10.2022.

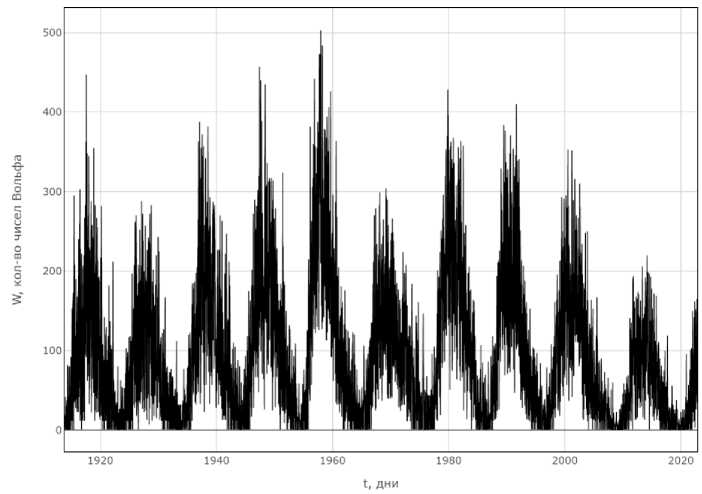
Рис. 1. Динамика чисел Вольфа

Ежедневная динамика солнечной активности не является стационарной. Коэффициент вариации ряда равен 90 %. Однако первые приращения чисел Вольфа оказываются стационарными, причем не только в широком смысле, но и в узком.

На рисунке 2 изображены первые разности исходного ряда Aw(t), оценки среднего значения и стандартного отклонения. В качестве временного лага при определении приращений чисел Вольфа был взят интервал, равный одному дню, тогда как первый и второй моменты рассчитывались на удвоенном 11-летнем цикле Солнечной активности, то есть данные усреднялись за 22 года.

На выделенном на рисунке 2 интервале с 7000 дня по 53200 день видно, что стандартное отклонение и среднее значение меняются незначительно.

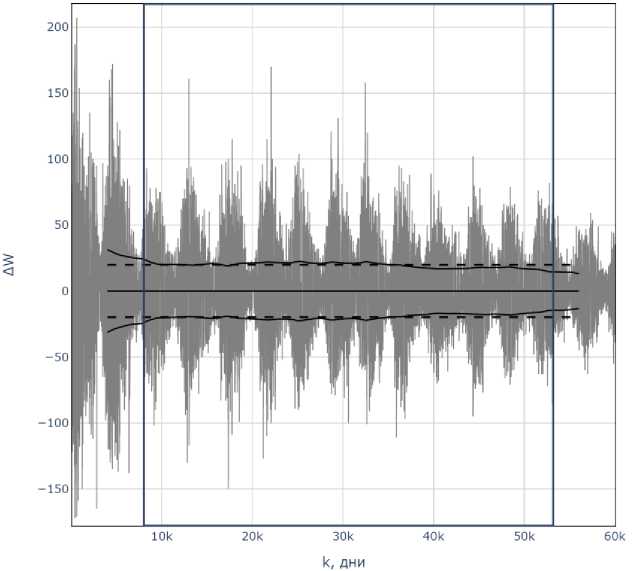
Рис. 2. Первые разности ежедневных данных

Различают стационарные случайные процессы в узком смысле и в широком смысле [3].

Случайный процесс называется стационарным в широком смысле (слабо стационарным), если его математическое ожидание и дисперсия не изменяются во времени, а автокорреляционная функция не зависит от абсолютного значения моментов времени t 1 ut₂, а зависит лишь от того, как далеко отстают они друг от друга во времени, то есть от разности времен т =

t 1 — t₂. Автокорреляционная функция для временного ряда х_г,...,х_п вычисляется по следующей формуле:

Л(т) =

и — т

п-т

^^X t+T

•X t .

t=1

Результат построения автокорреляционных функций для разных интервалов ежедневных приращений представлен на рисунке 3.

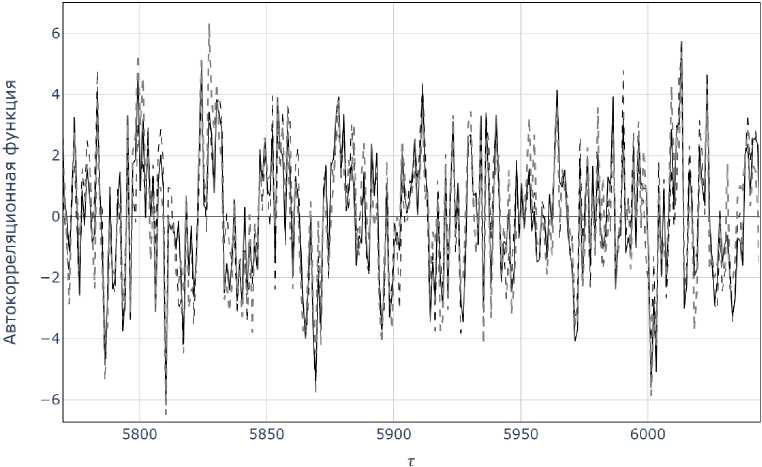
Рис. 3. Автокорреляционная функция

Наблюдается статистическая схожесть функций. Автокорреляционная функция не зависит от абсолютного значения моментов времени t 1 и t₂, а зависит лишь от т. Следовательно, ряд первых приращений ежедневных данных на интервале с 7000 дня по 53200 день стационарен в широком смысле.

Проверим, является ли процесс стационарным в узком смысле. Для этого необходимо, чтобы функции распределения F при разных началах отсчета совпадали [3].

Упорядочив первые разности чисел Вольфа по возрастанию, получим ранговое распределение, то есть зависимость упорядоченного значения от его порядкового номера (ранга) в упорядоченном ряду. Эта зависимость определяет обратную функцию распределения. Инверсия координатных осей и нормировка ранга по наибольшему количеству элементов приводят к интегральной функции распределения приращений чисел Вольфа [4].

Первые разности чисел Вольфа имеют симметричную плотность распределения, что характерно, например, для нормального или логистического закона распределения. Проведем сравнение этих двух законов распределения, для этого воспользуемся методом анаморфоз [4].

Интегральная функция логистического распределения задается уравнением:

F(x) =       (х-д)’

1 + е

где ц - среднее значение;

5 - параметр, пропорциональный стандартному отклонению ц = -^ • 5 [5].

Логарифмируя интегральную функцию распределения F(x), то есть уравнение (3), получим спрямляющее преобразование логистического закона, анаморфозу:

^|п(^^—1) = ^—Г^{(х —}^’     (4)

Таким образом, логистическая функция

спрямляется в координатах,

1))

^(x’^lnU )

—

. Эти координаты получили название

логистических координат (logistic scale).

Если в логистических координатах анали-

зируемые данные спрямляются, то логистический закон является адекватным их

описанием.

На рисунках 4 и 5 эмпирические распределения приращений чисел Вольфа,

взятые на разных временных интервалах,

представлены в координатах

1))

^(x’^lnG (X

—

Точками черного цвета показана эм-

пирическая функция распределения первых приращений чисел Вольфа, пунктир-

ной линией - теоретическое логистическое

распределение. В диапазоне (-6σ, +6σ) эмпирические данные практически совпадают с теоретической зависимостью. Следовательно, логистический закон является адекватным математическим описанием вероятностного распределения приращений чисел Вольфа.

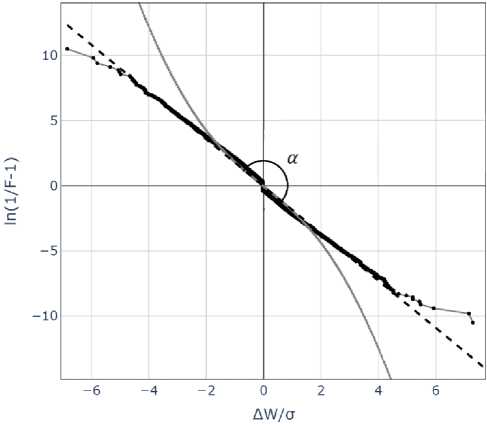
Рис. 4. Логистическая анаморфоза распределения приращений ежедневных чисел Вольфа, построенного для интервала с 1877 по 1977 гг. ц « 0, tga = 1.81

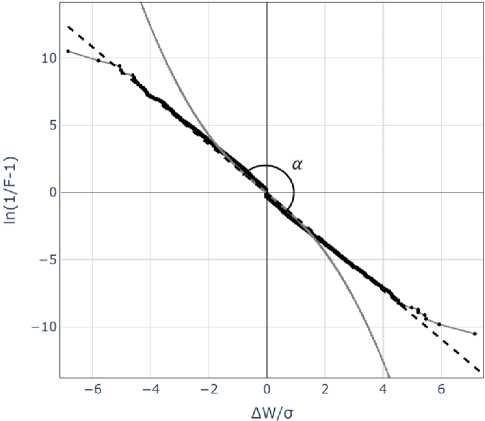
Рис. 5. Логистическая анаморфоза распределения приращений ежедневных чисел Вольфа, построенного для интервала с 1904 по 2004 гг. ц ~ 0,tga = 1.81

Прямая линия на плоскости определяется двумя параметрами: угловым коэффициентом и, например, координатой точки пересечения приближающей прямой с осью абсцисс. Поскольку графики анаморфоз на рисунках 4,5 проходят через начало координат, z ^ 0. Полученное значение параметра анаморфозы совпадает с оценкой математического ожидания, рассчитанной как средняя арифметическая временного ряда приращений чисел Вольфа.

В уравнении анаморфозы логистического закона (4) перейдем к безразмерному аргументу. Для этого нормируем шкалу абсцисс среднеквадратическим отклонением. В результате

|п(^-1) = -^.(1-^)

\ F(X) 7 S V г 7 X — Ц\ = I.8IM Г )

Если угловой коэффициент анаморфозы

• (4 ) равняется величине — —, то переход к безразмерному аргументу, нормированно-

• му средним квадратическим отклонением, изменит его значение и угловой коэффициент, согласно (5), станет равным -^ «

V3

• 1, 814. Идентификация углового коэффициента на графиках рисунков 4 и 5 дает именно это значение, 1.81. Таким образом, второй параметр анаморфозы, угловой коэффициент, оказывается также согласованным со второй статистической оценкой временного ряда чисел Вольфа, полученной как средняя арифметическая квадратов их приращений.

Для сравнения на тех же графиках в логистических координатах приводится теоретическое нормальное распределение, функция Лапласа, которая показана сплошной линией серого цвета. На уровне интегральных распределений, также как и для плотностей вероятностей, нормальное распределение совпадает с логистическим только в центральной части, на интервале от -1,4σ до 1,6σ. Вне этого диапазона исследуемые данные отклоняются от нормального распределения.

Итак, распределения приращений чисел Вольфа, построенные на разных времен- ных участках исходного временного ряда, остаются инвариантными; сохраняется логистический закон, что говорит о стационарности в узком смысле приращений чисел Вольфа.

Вывод. Ежедневная динамика чисел Вольфа определяет случайный процесс со стационарными приращениями, стационарность понимается в узком смысле. Вероятностное распределение приращений чисел Вольфа следует логистическому закону. Значения параметров логистической анаморфозы согласованы со статистическими характеристиками анализируемого ряда, вычисленными как арифметические средние приращений чисел Вольфа и их квадратов отклонений от среднего, то есть с оценками математического ожидания и стандартного отклонения.