Анализ течений при лазерно-акустической обработке нержавеющей стали AISI 316L

Введение ультразвука в технологические процессы, такие как создание литых деталей, сварка и наплавка, приводит в структуре металлов к дендритной фрагментации, что напрямую влияет на прочностные характеристики готовых конструкций. Дендритная фрагментация развивается при наличии полостей. Если материал в момент коллапса пузырьков-пустот подвергнуть воздействию ударных волн, произойдет инициирование дендритных ячеек в зоне размягчения закристаллизованного металла. В расплаве они перераспределятся под воздействием уже существующего в нем поля звуковых колебаний и приводят к росту числа центров кристаллизации. Наиболее полно изучены и представлены в литературе процессы в расплавах материала относительно больших масштабов [1 –3] . Описаны акустические течения, возникающие в ванне расплава, и образование кавитационных пузырьков. Показано, что при определенных частотах можно достичь гомогенной структуры в зоне термического воздействия.

Наряду с традиционными подходами получения структур с заданными свойствами сегодня бурно развивается новая область технологической науки — «аддитивные технологии».

Данный технологический процесс имеет особенности, которые осложняют его моделирование с помощью сформировавшихся подходов. Перечислим некоторые из особенностей:

– ванна расплава имеет малый масштаб;

– большие, по сравнению с литьем, скорости плавления и кристаллизации (порядка 10 ⁷ К/с) [4] вследствие использования источников энергии высокой мощности;

– трудность подведения источника ультразвука напрямую в жидкую фазу вещества, то есть требуется посредник в виде подложки;

– необходимость решения многофазных связанных задач термоупругости и тепломассопереноса.

Тем не менее в последние годы ряд исследователей достиг успехов в решении вышеперечисленных проблем. В работе [5] представлен способ изготовления турбинных лопаток из сплава Ti6Al4V в ультразвуковом поле путем прямой лазерной наплавки. Показано, что при наплавке образца твердость металла увеличивается более чем в 1.1 раза при наличии акустических колебаний с частотой 100 кГц и мощностью более 1 кВт. Акустические колебания приводят к образованию в структуре стали Ti6Al4V равноосных областей зерен. Варьируя частоту и мощность колебаний, можно выбирать зоны, где при наращивании образца следует сформировать равноосную структуру.

В работе [6] произведены расчет и верификация проволочно-дугового аддитивного производства изделия с введением ультразвуковых колебаний подложки, которой является пластина из стали AISI 1045. Показано, что ультразвук не влияет на качественную картину течения, но увеличивает общую скорость потока и, как следствие, тепломассоперенос, что способствует гомогенизации расплава. Авторами выполнен только CFD-расчет, то есть расчет в рамках вычислительной гидродинамики (Сomputational Fluid Dynamics) с введением ультразвука в граничные условия в виде переменного смещения подложки.

Оказалось, что ультразвуковое воздействие может ослабить растягивающее напряжение в верхней части сварного шва и немного повысить сжимающее напряжение в его нижней части [7] , что потенциально способствует улучшению механических свойств. Расчетный размер зоны, в которой фронт затвердевания восприимчив к ультразвуковой деформации, не превышает 1 мм [8] . Авторами осуществлены расчет и экспериментальная верификация влияния на ванну расплава поля ультразвука, сформированного высокочастотным импульсным лазером.

На основе реализованной в [9] многофазной модели влияния ультразвуковых колебаний на форму свободной поверхности в процессе лазерной сварки показано, что рабочая амплитуда воздействия на ванну расплава находится в промежутке от 4 до 6 мкм [9] . При амплитудах меньше 4 мкм форма ванны расплава не меняется, а при амплитуде более 6 мкм происходит расплескивание расплава.

Целью данной работы является моделирование процесса тепломассопереноса в кювете с расплавом стали AISI 316L под воздействием лазерного излучения в виде ультразвукового поля с учетом потерь энергии колебаний при переходе через твердую фазу материала, а также оценка воздействия ультразвукового поля на профиль течения в ванне расплава.

• 2.    Описание подхода к моделированию

• 3.    Постановка задачи

  • 3.1.    Управляющие уравнения

Исследовалось влияние на течение в ванне расплавленного металла колебаний, порожденных эффектом Марангони вследствие лазерного излучения. Последнее задавалось как гауссово распределение. Численное решение задачи течения подразумевало введение двух расчетных доменов, в одном из которых решалось дифференциальное уравнение упругости, а в другом — гидродинамическое дифференциальное уравнение с учетом полной энергии системы. Для приближения к процессу аддитивного производства оба домена представляли собой нержавеющую сталь AISI 316L в разных агрегатных состояниях — твердом и жидком. Деформация свободной поверхности не рассматривалась. Численные решения, получаемые методом конечных элементов в ANSYS Transient Structural и методом конечных объемов в ANSYS CFX, связывались при помощи модуля ANSYS System Coupling.

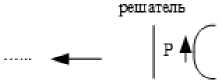
Передача данных решения задач прочности и гидродинамики, являющихся в обсуждаемом случае связанными, производилась в каждый момент времени в обе стороны таким образом: от прочностного решателя передавались показатели смещения на границе раздела доменов, а от гидродинамического решателя в прочностной — данные о силе воздействия в каждом узле на границе раздела доменов. Схема этой части алгоритма позаимствована в [10] и представлена на рисунке 1.

Распространение возмущений в произвольном твердом теле при переменном механическом воздействии, создаваемым внешним источником, в рамках теории упругости описывается классическим уравнением движения с учетом сил инерции, которое в векторной форме записывается как

∂ 2 u

V^ o+p F — p~^, (1)

∂t ²

где t — время, σ — тензор напряжений, F — вектор внешних объемных сил, ρ — плотность материала тела,

Инициализация гидре динамического расчета

Первая итерация

Гидродинамический решатель

Р

Передача сил в прочностной решатель

Прочностной Передача смещений в Гидродинамический

решатель

гидродинамический решатель

решатель

Начальное да впе ни е на интерфейсе

Деформация интерфейса из-за давления жидкости

Снижение давления из-за увеличения объёма

Вторая итерация

Передача сил в прочностной решатель

Гидродинамический

гидре динамический решатель

Рис. 1. Схема алгоритма связи задач прочности и гидродинамики

Увеличение давления из-за уменьшения объёма

Передача смешений в Прочностной

решатель

Деформация интерфейса в противоположном направлении

u — векторное поле смещений. При этом компоненты тензора напряжений представляются в виде:

E

Eν

° ^xx = 22(1 + v)^{£ xx +}(1 + v)(1 - 2v) E        Eν

° ^хх   2(1+) ^{e yx +} (1+v)(1 - 2v)

E        Eν vzz   2(1+) ezz +(1 + v )(1-2v)

EE

^(e XX ^{+ e} zz ),

^{( e} xx +^ zz ),

^(e xx + ^e xx ),

E

° ^xy =²2(1 + v) ^e x^y ’ ^z = ²2(1 + v) ^e yz ’ ° ^xz = ²2(1+v) ^e xz ’

где E — модуль Юнга, v — коэффициент Пуассона, eij — относительная деформация, (i,j = 1, 2, 3). Здесь деформации записываются как exx = dX, e

yy

∂u _y ∂y ^,

∂uz ezz   q ∂z

∂ux ∂uy exy exyx dy + dx , exyz e-

y ∂uz zx dz + dy'

∂u

y

∂u x ∂u y

^2e xy ^2e yx    dy ⁺ dx ,

где u i — смещения при i = x,y,z .

После подстановки сначала компонент тензора деформаций (3) в (2) и затем полученных выражений для компонент напряжений в (1) получим уравнения равновесия в перемещениях или уравнения Ламе. В векторной форме их запись выглядит так:

р ^-u = (А+^) V ² ^ u +^ ^ u +p F , ∂t ²

где λ и µ — коэффициенты Ламе, F — вектор массовых сил.

Перенос тепла в материале в общем виде представляется уравнением:

∂T pcp    + v •VT 1= VkVT+Q,

∂t

где ρ — плотность материала, c p — удельная теплоемкость, T — скалярное поле температуры, v — векторное поле скорости, ∇ — оператор набла, k — коэффициент теплопроводности, Q — объемный источник тепла. При этом ρ , c p , k являются функциями температуры.

Движение свободной поверхности расплава в ванне происходит за счет ненулевого градиента поверхностного натяжения и изменения плотности в ванне расплава в зависимости от температуры. Следовательно, систему уравнений (1) – (5) должны дополнять уравнения сохранения:

1 ^{+ V} (p v ) = ^0,

P\d + (vV)v j = -Vp+nV2v+pf, где p — давление, η — зависящая от температуры динамическая вязкость, f — массовые силы.

• 3.2.    Математическое описание особенностей рассматриваемой задачи

На свободной поверхности жидкого домена задается тепловой поток, который выражается так:

∂T (8) q    k~^    qlas + qconv +qrad, ∂n P .       .     (x-xo)2+(y-yo)2 (9) qlas = Пг2 (1—R)e        r2       , qconv = —hc(T-To) (10) qrad = -^ (Т4 — TO ) , (11) где k — коэффициент теплопроводности, n — вектор нормали к поверхности, qlas — тепловой поток лазера, qconv — конвективная теплоотдача, qrad — радиационная теплоотдача, P — мощность лазерного излучения, x0,y0 — координаты центра лазерного пятна, заданные в декартовой системе координат, r — радиус лазерного пятна, hc — коэффициент конвекции, T0 — температура внешней среды за пределами кюветы с расплавом, ε — коэффициент излучения поверхности расплава, σ — постоянная Больцмана, R — коэффициент отражения.

Также на свободной поверхности жидкого металла ставится условие термокапиллярной конвекции:

∂ v ∂γ ∂T ^η∂ n ∂T ∂ s ^,

где η — динамическая вязкость, γ — коэффициент поверхностного натяжения, n — вектор нормали к поверхности, s — вектор, касательный к свободной поверхности жидкого домена.

На верхней поверхности твердого домена полагаются нулевые.

Механические колебания подложки, роль которой в решаемой задаче выполняет дно кюветы с металлом, задаются как переменное смещение:

u z (t) = (A/2) + (A/2)sin(2ntv — n/2),

где A — амплитуда колебаний, ν — частота колебаний. На остальных стенках кюветы с расплавом выполняются условия свободных колебаний и нулевого теплового потока.

• 4.    Физическо-механические свойства стали AISI 316L

• 5.    Описание аппроксимации и дискретизации

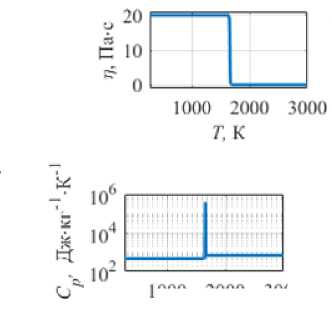
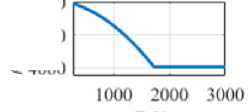
Физико-механические свойства нержавеющей стали AISI 316L в твердом и жидком агрегатных состояниях с указанием литературных источников, откуда взяты данные о материале, представлены в таблице 1, а теплофизические свойства содержит рисунок 2.

Для учета фазового перехода из твердого состояния в жидкое в интервале температуры между линиями солидуса и ликвидуса представим удельную теплоемкость и динамическую вязкость как сигмоидальные функции температуры:

n(T )= n L + (n s — П ь ) /( 1+е T-aTm ) , (14)

C p (T ) = C pL + (C pS — C pL ) /( 1 + e T - Tm ) + H m •e - 2 , (15)

где ηL — динамическая вязкость жидкого металла, ηS— динамическая вязкость твердого металла, CpL — удельная теплоемкость жидкого металла, CpS — удельная теплоемкость твердого металла, Hm — скрытая теплота плавления, Tm — температура плавления, равная среднему значению между температурой солидуса и ликвидуса, a — температурный коэффициент плавности сигмоидального перехода.

Расчетная область представляется в виде двух параллелепипедов (доменов): жидкого и твердого. Размеры доменов указаны на рисунке 3. Источник лазерного излучения (он же источник нагрева) располагается в центре свободной поверхности жидкого домена.

Размеры элементов аппроксимирующей ванну расплава расчетной сетки у жидкого и твердого домена различались и подбирались экспериментально, исходя из оптимального соотношения качество металла–скорость течения. Применялась регулярная тетрагональная сетка, при этом число элементов для жидкого домена составляло 1920 с размером стороны ячейки 2.5 · 10 ^-3 мм, для твердого домена — 63000 с размером стороны 4 · 10 ^-4 мм. Параметры нагрева и параметры на входах в решатели представлены в таблице 2. Начальная температура жидкого домена принималась равной 1673 К, то есть температуре ликвидуса.

Функция (13) механического отклика (смещения) подложки на лазерное воздействие представляет собой синусоиду со сдвигом по фазе на четверть (см. Рис. 4а ). Такое описание выбрано для того, чтобы начальное смещение равнялось нулю, а амплитуда колебаний — 1 мкм; частота колебаний составляет 100 кГц. Символами «*» на графике отмечены контрольные точки, в которых проводился анализ влияния лазерного воздействия на

( a )

( б )

( г )

£ 4000

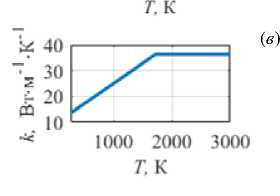
Таблица 1. Физическо-механические свойства стали

Параметр	Обозначение	Значение	Единица измерения	Источник
Температура ликвидуса	TL	1673	К	[11]
Температура солидуса	TS	1649	К	[11]
Скрытая теплота плавления	Hm	4·105	Дж/кг	[12]
Коэффициент конвекции	hc	5	Вт/(м 2· К)	[13]
Коэффициент излучения поверхности	ε	0.8	–	[14]
Динамическая вязкость в жидком состоянии	η	0.006	Па · с	[15]
Динамическая вязкость в твердом состоянии	ηS	20	Па · с	–
Удельная теплоемкость жидкого металла	CpL	458.98	Дж/(кг · К)	[16]
Удельная теплоемкость твердого металла	CpS	692.98	1Дж/(кг · К)	[16]
Градиент поверхностного натяжения жидкого металла	∂γ/∂T	0.00019	Дж/(кг · К)	[17]
Температура плавления	Tm	1660	К	–
Температурный коэффициент плавности сигмоидального перехода	a	3	К	–
Коэффициент отражения поверхности	R	0.5	–	–
Постоянная Больцмана	σ	5.6·108	Дж/К	–
Модуль Юнга	E	2·1011	Па	[18]
Коэффициент Пуассона	ν	0.3	–	[18]

1000 2000 3000

Г. К

Рис. 2. Теплофизические свойства стали AISI 316L: плотность ( а ), теплопроводность ( б ), динамическая вязкость ( в ), удельная теплоемкость ( г )

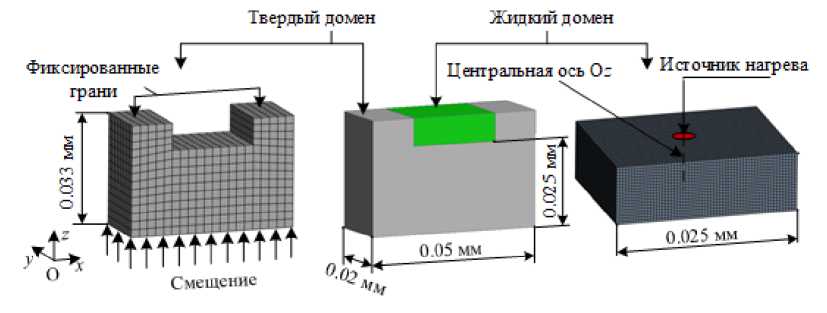
Рис. 3. Расчетная область (слева направо): твердый домен, общий вид, жидкий домен поток в жидкой ванне расплава нержавеющей стали AISI 316L.

• 6.    Результаты моделирования и сравнение

Рассматривается влияние периодического лазерного воздействия на ванну расплава в точках, указанных на рисунке 4а . На рисунке 5 в моменты времени, когда фронт волны колебаний достигает этих точек, приведены графики скорости течения в направлении оси Oz в жидком домене, то есть при 2.5 <  zz х 105) <  3.3 м, в условиях ультразвукового воздействия ( v _z ^∗ ) и без него, только за счет конвекции Марангони ( v z ).

В моменты времени, в которые амплитуда колебаний максимальна и минимальна (контрольные точки b, d, f, h, j, l), скорость потока с ультразвуковым воздействием и без него подобны друг другу, так как смещения (деформации) элементов сетки нулевые. При средней амплитуде колебаний (точки a, e, i) наблюдается торможение потока вследствие движения деформируемой нижней поверхности жидкого домена вверх, в то время как в точках с, g, k поток ускоряется вследствие движения деформируемой поверхности вниз. При таком периодическом

Таблица 2. Параметры задачи

Параметр	Значение	Единица измерения
Мощность нагрева	0.1	Вт
Радиус пятна нагрева	0.01	мм
Шаг по времени	2.5·10-8	с
Время начала нагрева	0	с
Продолжительность расчета	3·10-5	с
Температура внешней среды T 0	300	К

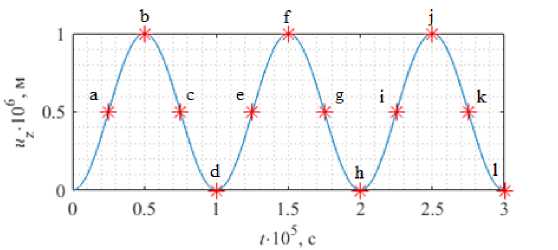
( a )

Рис. 4. График функции, описывающий во времени смещение вверх-вниз по оси Oz нижней части твердого домена ( а ) и иллюстрации деформации жидкого домена в контрольно-временных точках d–h ( б )

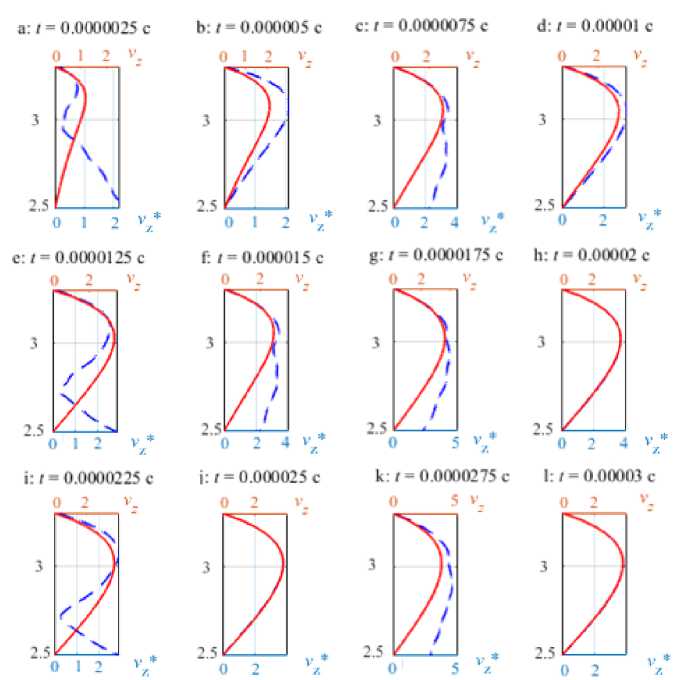
Рис. 5. Графики скоростей течения в жидком домене вдоль центральной оси Oz при ультразвуковом воздействии – v_z^∗ · 10⁵ м/c (штриховая линия), и без него – vz · 10⁵ м/c (сплошная линия)

движении поверхности на скорости движения металла в жидком домене влияет импульс деформации.

В таблице 3 приведены результаты анализа максимальной скорости течения в жидком домене вдоль центральной оси с учетом ультразвукового воздействия и без него. Расчет относительной разности значений рассчитывался по формуле:

∗ R = f-z--z^ -100%, vz где vz∗ и vz — максимальная скорость, соответственно, с учетом и без учета ультразвуковых колебаний.

Данные в контрольно-временных точках c, g, k, представленные в таблице 3, количественно подтверждают сделанное выше утверждение о том, что при движении деформируемой поверхности вниз, происходит ускорение течения. Противоположное высказывание справедливо для точек e, i. В контрольной точке a наблюдается высокая положительная относительная разность скоростей вследствие того, что влияние на течение металла конвекции Марангони в начальный момент времени на порядок меньше, чем передаваемых от подложки импульсов колебаний. Это объясняется малым градиентом температуры от воздействия лазерного источника на поверхности жидкого домена и, как следствие, медленно развивающимся конвекционным течением. На рисунке 6 в контрольно-временных точках (см. Рис. 4а ) для сравнения приведены картины полей скорости в ультразвуковом поле и без него в перпендикулярном плоскости Oxz сечении на половине высоты жидкого домена.

На картинах, отвечающих контрольно-временным точкам a, c, d, g, i, k, наблюдается сглаживание скалярного поля скорости в нижней части жидкого домена вследствие передачи импульса движения от деформируемой поверхности. Выводы о пропорциональности скорости течения в точках b, d, f, h, j, l на центральной оси Oz также справедливы и для скалярного поля расчетного домена.

Качественно картины течения совпадают с работой [6] , в которой исследовалась похожая ситуация, но с иной геометрией расчетной области и без учета потерь энергии при прохождении отклика ультразвуковых колебаний через твердый домен.

Таблица 3. К сравнению максимальной скорости течения в контрольных точках жидкого домена с учетом и без учета ультразвукового воздействия

Точки	vz∗ , м/с	vz , м/с	Относительная разность, %
a	0.000246948	0.000111758	120.97
c	0.000340184	0.000269938	26.02
e	0.000291001	0.000331612	–12.25
g	0.000415278	0.000356166	16.60
i	0.000292412	0.000366164	–20.15
k	0.000431457	0.000370363	16.50

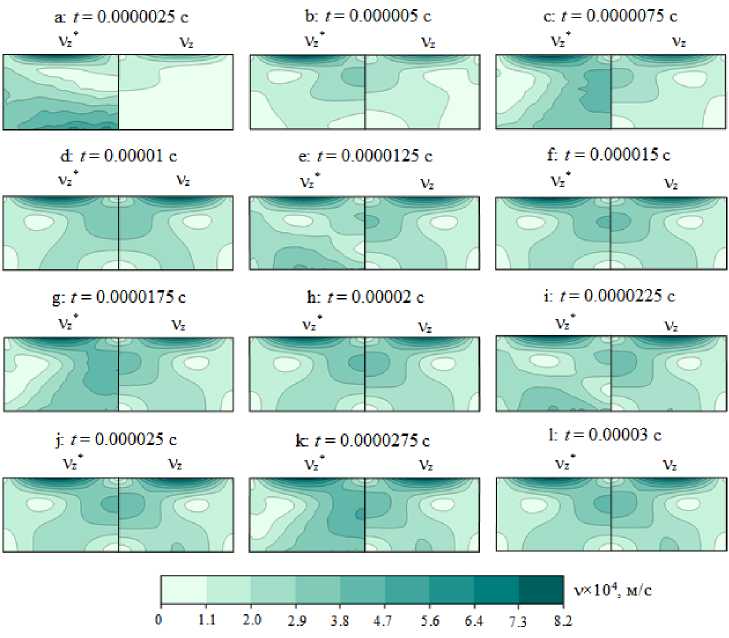
Рис. 6. Поля скоростей течения при ультразвуковых колебаниях ( v_z^∗ ) и без них ( vz )

• 7.    Заключение

Рассмотрена созданная трехмерная имитационная гидродинамическая модель процесса лазерной сварки при отсутствии и наличии ультразвукового воздействия на ванну расплава через твердую часть металла. В последнем случае учитывается конвекция Марангони на поверхности расплава.

Вычислительные эксперименты показали:

– моделирование процессов лазерной сварки c ультразвуковым воздействием возможно при применении инструментария вида ANSYS System Coupling, позволяющего решить связанную задачу гидродинамики и прочности;

– в моменты времени, в которые амплитуда колебаний ультразвуковой волны имеет максимум или минимум, скалярное и векторное поля скорости с ультразвуковым воздействием и без него пропорциональны. Изменение скорости течения минимально вследствие нулевой деформации поверхности жидкого металла, не получающей дополнительного импульса воздействия на поток;

– в моменты времени, которым соответствует среднее значение амплитуды колебаний, скалярное и векторное поля скорости при ультразвуковом воздействии и без него непропорциональны. Передаваемый импульс движения деформируемой твердой поверхности интенсифицирует скорость течения при движении (деформации) объема жидкого металла вниз и тормозит течение при движении (деформации) его вверх. В обоих случаях отмечено, что деформация приводит к сглаживанию скалярного поля скорости на нижней части жидкого объема.

Исследования по формированию течений в ванне расплава с учетом конвекции Марангони в результате высоконцентрированного лазерного излучения осуществлены за счет гранта Российского научного фонда (проект №23-29-00219) Разработка алгоритмов связи теплопрочностного и гидродинамического решателей и последующее исследование влияния ультразвука на течение выполнены в рамках Программы стратегического академического лидерства Казанского национального исследовательский технического университета имени А.Н. Туполева («ПРИОРИТЕТ–2030»).