Анализ уравнений девиации геодезических в метрике Шварцшильда

Впервые уравнение девиации геодезических получил Леви-Чевита в 1925 году при рассмотрении двух бесконечно близких геодезических в искривленном n-мерном пространстве. В [1] получен общий вид решений для 3- и 4-мерного риманова пространства и как частный случай приведено решение в метрике Шварцшильда без конкретизации вектора 4-скорости. Ранее общий вид решения для сферически-симметричного четырехмерного пространства был получен в [3]. Классическим описанием приливных сил в сферически-симметричной стационарной метрике является задача в [2] для тела прямоугольной формы, двигающегося со скоростью много меньше скорости света. Ссылаясь на уравнения, полученные в [3], Д. Филипп и другие [4], [5] нашли ньютоновское приближение уравнений девиации и уравнения орбит для двух спутников в гравитационном поле Земли и провели сравнения с релятивистским случаем в метрики Шварцшильда. В [6] рассмотрена одномерная гидродинамическая модель звезды, двигающейся вокруг шварцшильдовской черной дыры по параболической орбите. В отличии от ряда приведенных выше работ мы рассмотрели общий случай в сильном гравитационном поле, что имеет место у горизонта.

В ряде статей [7], [8] приведено решение уравнений девиации геодезических для заряженных черных дыр Райсснера-Нордстрёма. Данное решение является также как и решение Шварцшильда сферически-симметричным решением в вакууме, но отличается наличием у черной дыры электрического заряда и двух горизонтов событий. Эти исследования представляют исключительно теоретический интерес, так как заряженных черных дыр в природе не наблюдается [9].

Изучение девиации геодезических в метрике Шварцшильда важно для понимания приливного разрушения звезд, деформации аккреционных дисков и тому подобного вблизи черных дыр.

Целью этой работы является исследование влияния скорости (энергии) частицы и расстояния до горизонта на знак компонент вектора приливного ускорения в метрике Шварцшильда. Такое изменение говорит о том, что в зависимости от скорости частицы (или расстояния до горизонта) приливное сжатие меняется на растяжение. Получены точные решения уравнений девиации геодезических для: 1. частиц только с радиальной скоростью; 2. частиц на круговой орбите; 3. частиц с радиальной и круговой составляющими скорости.

В первой части приводится общий вид уравнения девиации геодезических. Во второй части приведено решение уравнения геодезического отклонения для частиц с радиальной скоростью. В третьей части показаны решения для частиц с круговой скоростью и общий случай движения частиц по спирали. В заключении приведены некоторые приближенные расчеты для работы приливных сил.

В статье расчеты выполнены в геометрической системе единиц c = G = 1, латинские индексы пробегают значения от 0 до 3 и выбрана сигнатура метрики - 2. Координаты r и t измеряются в единицах GMc ^{- 2} и GMc ^{- 3} соответственно. Тестовая частица имеет единичную массу. Все расчеты приведены в координатах Шварцшильда.

1. Уравнение девиации геодезических

Мы не будем подробно останавливаться на выводе уравнения девиации геодезических, изложим только постановку задачи и основные выводы следующие из уравнений в общем виде. Более подробный вывод смотри в [10], [11].

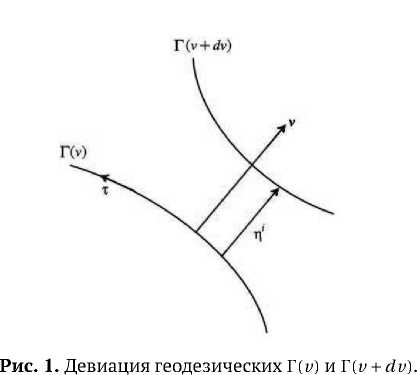
Рассмотрим относительное 4-ускорение двух тестовых частиц на бесконечно близких геодезических Г( v ) и Г( v + dv ), таких что координаты точек на них описываются функциями x i = x i ( т , v ), причем т является аффинным параметром вдоль геодезической, v перпендикулярен касательному вектору и остается постоянным вдоль каждой кривой (см. Рис.1). Расстояние между этими геодезическими удобно описывать бесконечно малым 4-вектором отклонения η ⁱ . В процессе движения одной тестовой частицы относительно другой, величина вектора отклонения меняется по закону:

D ² i

"5^ + R ikm U j n k u m = 0,

(1.1)

где R ikm = g^iIR ijkm — тензор Римана, и¹ — 4-скорость одной частицы относительно другой.

(2.1)

g ⁰⁰ _ ( 1 - 2 м ) ^{- 1} ,

g g g

• 11 _

22 _{_}

-

-

.33 _

-

£1 - M , r ²            '- 1

( r ² sin ² 6 ) ,

(2.2)

компоненты тензора кривизны:

M R 0101 - R 0303 - - Т Г ’ R 0202 -- R 1313 - 2^’                                  (2.3) M R 2323 - R 1212 - r^

Движение массивных частиц в окрестности черной дыры описывается времениподобными гео-

дезическими [12]: E t    1-2M/ r ’ r2 - E2- (1 - M) ! + Ц .          1 r Л r2 Г                                      (2.4) 6 - 0’ Ф - L’ где точкой, также как и в уравнении (1.1), обозначено дифференцирование по аффинному параметру τ, который для массивных частиц играет роль собственного времени, E — удельная энергия частицы и L — ее удельный угловой момент. Причем правые части уравнений t иг2 больше нуля, так как движение происходит вперед во времени и подкоренное выражение больше нуля соответственно.

Остановимся более подробно на описании радиального движения частиц. В координатах Шварцшильда рассмотрение радиального движения возможно только до горизонта. Для такого движения нулевая и первая компонента вектора 4-скорости отличны от нуля:

u l - ( u 0 ’ u 1 ’0’0 ) .                                              (2.5)

Выражений для ненулевых компонент скорости (2.5) подчинятся условию нормировки [13]:

g ik u^lu k - 1.

(2.6)

Чтобы удовлетворялось условие нормировки (2.6) за нулевую и первую компоненты вектора 4-скорости (2.5) можно принять уравнения геодезических (2.4) t и r , тогда:

u = [ dr ’ dr ’°’ ⁰) •                                   (2.7)

dτ dτ

Девиация геодезических, падающих радиально в поле невращающейся черной дыры, описывается уравнениями, полученными на основе (1.1), (2.5):

Dn - - g 00 R 0101 u 1 ( u 0 + u 1 ) - [ 1 - —I - 1 M d т 2                                   V r ) r 3	u 1 ( u 0 + u 1 ) >  0’	(2.8)
D 2 п 1-Г1Р   „ (u 0 + M1)- fl 2 M 1 Mu' d т 2 - g R 0101 u u + u J- p r J r 3 u	0 ( u 0 + u 1 ) >  0’	(2.9)
d т 2 - g ( R 0202 ( u ) + R 1212 ( u )) - r 5 (2 (	u 0 ) 2 + ( u 1 ) 2 ) <  0’	(2.10)
Dn 3 - g 33( R 0303 ( u0)2 + R ,3,3 ( u -) 2) - V M 35 (l dт 2        V                         / r 5 sin 2 6 V	( u 0 ) 2 + 2 ( u 1 ) 2 ) >  0.	(2.11)

Компоненты скорости в уравнениях (2.8)-(2.11) больше нуля на любых расстояниях от горизонта, следовательно можно точно определить знак приливного ускорения для ультрарелятивист-ских частиц. Так как уравнения девиации (2.8)-(2.11) являются координатно-зависимыми, на горизонте t -, θ -, φ -компоненты приливного ускорения стремятся к бесконечности, а r прерывается на горизонте. Из уравнений (2.8)-(2.11) явным образом не видно отличий релятивистских частиц от классических. Энергию релятивистской частицы ( m - 1) можно представить в виде [10]:

E - Y V g °° ’ (2.12)

где γ — Лоренц-фактор. Следовательно вектор девиации геодезических для классического и уль-трарелятивистского случая различается в зависимости от энергии. Движение с классическими скоростями характеризуется у —* 1 и, следовательно, E —> V g °° • Таким образом, если значения энергии превышают _x/ g °° , то частицы имеют ультрарелятивистскую скорость.

Проведем анализ уравнений (2.8)-(2.11). Известно, что при малых скоростях удельная энергия частиц стремится к ^/ g 00 , тогда:

₀ .     (    2 M Г^1/2   1   .

u = t —* 11--I , u = r —* 0.

(2.13)

Учитывая выражения (2.13), уравнения девиации геодезических для нерелятивистских ча-

стиц имеют вид:

D 2 η 0 = 0-                                        (2-14) dτ 2 D ^- = g11R 0101 ( u 0 ) 2 = M >  0-                          (2-15) dτ 2                       r 3 D 2 П 2    22       0^2    2 M -2    2 M V1 dT 2 = g R 0202 ( u ) = r 3 r p     r j < 0-                    (2.16) Ddn = g 33 R 0303 ( u 0 ) 2 = ( r 2 sin 2 в Г‘ M ( 1 - 2 M ) " ' >  0.               (2.17)

Из уравнений (2.15)-(2.17) следует, на удаленном расстоянии от горизонта r — и φ — компоненты приливного ускорения больше нуля и возрастают с уменьшением расстояния до горизонта. Компонента θ меньше нуля и при приближении к горизонту уменьшается. Таким образом, вдали от горизонта тело с нерелятивистской скоростью растягивается в радиальном и азимутальном направлениях, вдоль полярного направления тело сжимается.

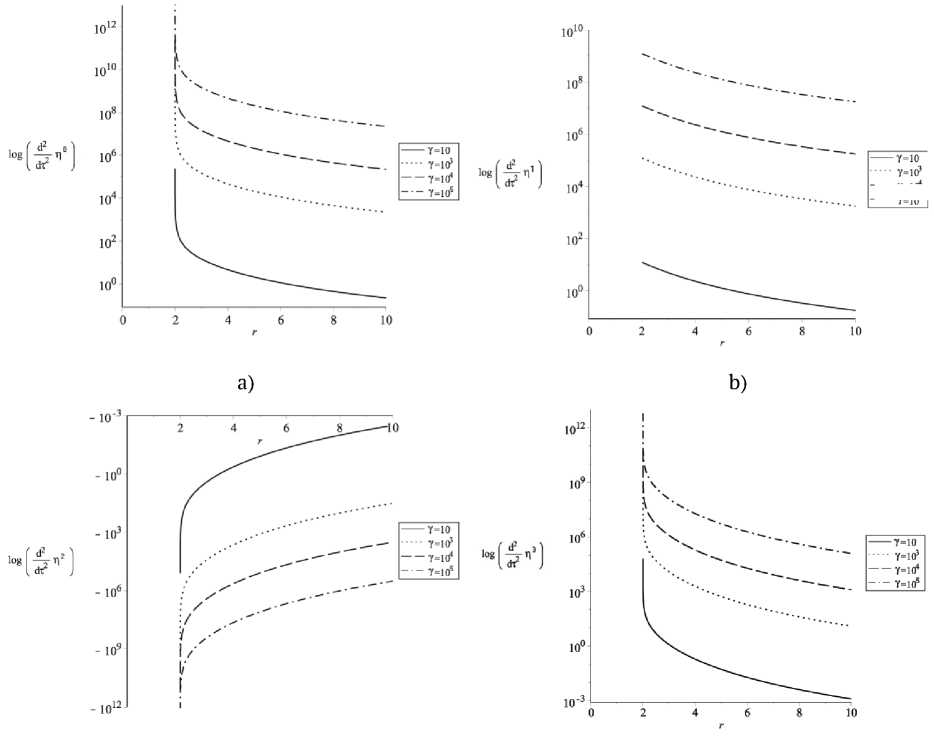
Зависимости для релятивистских частиц при различных энергиях приведены на рисунке 2, где наглядно видно, что θ —компонента 4-вектора приливного ускорения меньше нуля и уменьшается еще больше при уменьшении энергии частицы, t —, r — и φ — положительны и возрастают при приближении к горизонту, однако радиальная компонента не стремится асимптотически к бесконечности. Все компоненты приливного ускорения асимптотически стремятся к нулю на бесконечно удаленном расстоянии от черной дыры и с увеличением энергии частиц возрастают компоненты вектора девиации.

То есть, тело только с радиальной релятивистской скоростью при стремлении к горизонту шварцшильдовской черной дыры растягивается вдоль радиального и азимутального направлений и сжимается в полярном направлении. При переходе от релятивистских скоростей к малым скоростям приливные ускорения ведут себя аналогичным образом. Отличительной особенностью релятивистского случая является наличие ненулевой t -компоненты 4-ускорения.

u i = ( u ⁰ ,0,0, u 3 ) = d -0-0- dτ

dφ dτ

(3.1)

Согласно [14] круговые орбиты могут могут существовать до расстояний r min = 3 M , причем при r <  6 M орбиты неустойчивы, а при r >  6 M — устойчивы. Такие круговые орбиты характеризуются следующими удельным угловым моментом и удельной энергией:

Mr ²

L ² =-------

(3.2)

r - 3 M

E ² =

( r - 2 M ) ² r ( r - 3 M ) ■

(3.3)

С учетом (3.1) и (1.1) уравнения девиации геодезических для круговой орбиты имеют вид:

D ² η ⁰ dτ ²

- g ⁰⁰ R 0303 u ⁰ ( u ⁰ + u ³⁾ = ( 1 - 2 M j  ( M j u ⁰ ( u ⁰ + u ³⁾ >  0-

(3.4)

d)

c)

Рис. 2. Зависимости компонент вектора девиации геодезических от расстояния при различных значениях Лоренц-фактора. Ось ординат приведена в логарифмическом масштабе, t - φ — компоненты приведены на рисунках a)-d) соответственно. Масса черной дыры M = 1 , минимальное расстояние до горизонта 10 - 4 г^ .

--Y=10*

---Y=1(l5

D£ = g .. ⁽ R _ии ⁽ u 0 ) 2 + R 1313 ⁽ u 3 ) 2 ) = (1 - MM (( u 0 ) 2 + 2 ( u 3 ) 2 ) >  0, "dT F = g ²² ( R 0202 ( u 0 ) 2 ⁺ R 2323 ( u ³ ) 2 ) = ^- Г 2 ( Г 3 )(² ( u 0 ) 2 ⁺ ( u ³) 2 ) <  0, d ^П = g ³³ R ₀₃₀₃ u ⁰ ( u ⁰ + u ³) = ( г ² sin ² 6 ) ¹ ( 33 ) u ⁰ ( u ⁰ + u ³ ) >  0.

(3.5)

(3.6)

(3.7)

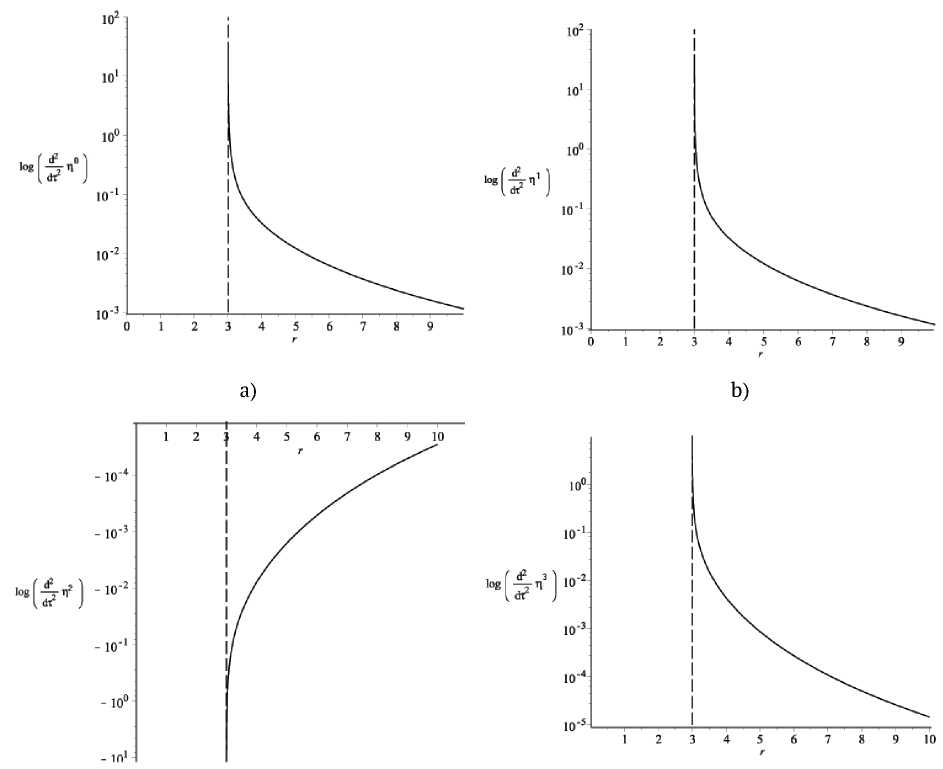
Из уравнений для кругового движения (3.4)-(3.7) видно, что знаки компонент 4-вектора приливного ускорения аналогичны знакам при радиальном падении. Однако, вид зависимости компонент вектора девиации несколько отличается от случая радиального движения и приведен на рисунке 3. Графики на рисунке 3 имеют более резкое возрастание по сравнению с графиками на рисунке 2 при стремлении к минимально возможному расстоянию существования круговых орбит.

Более общий вид уравнения девиации геодезических принимают при наличии у частицы как круговой так и радиальной компонент скорости и имеют следующий вид:

D ² η ⁰ dτ ²

- g ⁰⁰ [ R 0101 u ¹ ( u ⁰ + u 1 ) + R 0303 u ⁰ ( u ⁰ + u ³ )] >  0,

(3.8)

D ² η ¹ dτ ²

= g ¹¹ [ R 0101 u ⁰ ( u ⁰ + u 1 ) + R 1313 u ³ ( u ³ - u ¹ )] >  0,

(3.9)

d)

c)

Рис. 3. Зависимости компонент вектора девиации геодезических от расстояния при удельном моменте (3.2) и удельной энергии (3.3). Ось ординат приведена в логарифмическом масштабе. t - φ — компоненты приведены на рисунках a)-d) соответственно. Масса черной дыры M = 1 , минимальное расстояние г min = 3 M .

D V d т ²

= g ²² [ R 0202 ( u ° ) + R 1212 ( u 1 ) + R 2323 ( u 3 ) ] <  0,

D ² n ³ d т т

= g ³³ [ R 0303 u ° ( u ° + u ³ ) + R 1313 u ¹ ( u ¹ - u ³ )] >  °,

(3.10)

(3.11)

В этом случае вид удельной энергии совпадает с (2.11), а ограничения на удельный угловой момент получаются из условия положительности или равенстве нулю подкоренного выражения для r.

Знаки компонент вектора приливного ускорения и их зависимости от расстояния в общем случае (уравнения (3.8)-(3.11)) для релятивистских частиц аналогичны предыдущим случаям. При переходе к классическим скоростям уравнения девиации для общего случая (3.8)-(3.11) переходят в уравнения (3.4)-(3.7). Вид зависимостей для общего случая аналогичен виду для радиального случая и здесь не приводится.

Заключение

Анализ уравнений девиации геодезических показывает, что знаки компонент приливного ускорения, и соответственно приливных сил, в метрике Шварцшильда не меняются в зависимости от скорости частицы, параметров геодезической или черной дыры. Вдоль радиального и азимутального направлений всегда наблюдается приливное растяжения, а вдоль полярного - сжатие. Наличие ненулевой положительной t-компоненты для ультрарелятивиситских частиц и классических частиц на круговых орбитах говорит о том, что в результате девиации частицы излучают энергию.

Из полученных уравнений, по аналогии с классическим выражением для работы, можно приблизительно рассчитать работу приливных сил по отклонению частиц. Для примера здесь приведены данные для двух радиально двигающихся протонов, отклоняющихся друг от друга на расстояние комптоновской длины волны. Изначально протоны находятся на расстоянии 10 - 5 r g от горизонта черной дыры массой 10 6 M ₀ . Расчеты приведены в таблице 1.

Таблица 1. Работа по отклонению протонов вдоль определенных направлений в зависимости от разных значений энергий (Лоренц-факторов) частиц, двигающихся с радиальной скоростью

γ	W r (эВ)	W θ (эВ)	W φ (эВ)
1	1.05 х 10 - 16	- 5.23 х 10 - 12	2.62 х 10 - 12
10 2	1.05 х 10 - 12	- 5.23 х 10 - 8	2.62 х 10 - 8
10 3	1.05 х 10 - 10	- 5.23 х 10 - 6	2.62 х 10 - 6
10 4	1.05 х 10 - 8	- 5.23 х 10 - 4	2.62 х 10 - 4
10 18	1.05 х 10 20	- 5.23 х 10 24	2.62 х 10 24

Из таблицы 1 видно, что при увеличении γ -фактора (первый столбец) соответствующие значения работы вдоль каждого направления возрастают быстрее. Из вида зависимостей для вектора девиации от расстояния (Рис.2) следует, что работа приливных сил при приближении к горизонту неограниченно увеличивается. В последней строке приведены значения работы приливных сил при y = 10 ¹⁸ . Такие значения работы сил девиации необходимы при рождении частиц в поле статической черной дыры. В реальных условиях вблизи шварцшильдовских черных дыр скорости столь близкие к скорости света недостижимы за конечный промежуток времени.

Автор выражает особую благодарность научному руководителю д.ф.-м.н., проф. Андрею Анатольевичу Грибу за обсуждение работы и ценные замечания.