Анализ условий применения статической детерминированной модели, модифицированной для случая скачкоообразного увеличения стоимости запасов

В экономической литературе часто упоминается классическая статическая детерминированная модель (EOQ) управления запасами. При использовании EOQ оптимальный размер партии рассчитывается по формуле [1]:

.             р

Q * = _л 2 • D

N       I • C

где D – величина спроса на позицию запасов, P – затраты на доставку одной партии материала, I – отношение величины издержек хранения единицы материала к стоимости единицы материала в единицу времени, С – цена единицы материала. Время между поступлениями партий запасаемого материала на склад (длина цикла) равно:

T ц =Q*/D (2)

Одним из существенных недостатков модели EOQ является то, что в ней не рассматривается случай внезапного скачкообразного увеличения стоимости запасаемых материалов [2]. Однако, как показывает экономическая практика, такие прогнозируемые скачкообразные изменения закупочных цен реализуются в заметном числе случаев. В условиях ожидаемого скачкообразного увеличения стоимости единицы запасаемого материала и стоимости доставки партии можно использовать модифицированную для случая скачкообразного увеличения стоимости запасов статическую детерминированную модель (МСДМ) [3], с учетом ограничений по срокам хранения запасов.

В МСДМ оптимальный объем материалов, который необходимо запасти определяется по формуле:

D • C ₂ У 2 • D • C ₂ • P ₂    D

I • C 1          C 1 • 7I         I

где Q* 1 – величина создаваемого запаса материала определенного вида, который необходимо закупить до увеличения цены на материал, С 1 – цена единицы материала до скачкообразного увеличения, P 1 – стоимость доставки партии до ее увеличения, I – отношение величины издержек хранения единицы материала к цене единицы материала в единицу времени, D – спрос на запасаемый материал в единицу времени, С 2 –цена единицы материала после увеличения, P 2 – стоимость доставки партии материала после ее увеличения.

Обозначим продолжительность планового периода как T . Плановый период разобьем на две части. В первой части происходит уменьшение закупленной до уве- личения цены партии запаса материала, тогда продолжительность первой части планового периода определяется отноше-∗ нием   . Во второй части планового пе- риода осуществляются поставки материала партиями, размера Q2, через равные промежутки времени, обозначаемые Tц, тогда продолжительность второй части планово-∗ го периода составляет (Т-  ).

Размер партии на пополнение запаса во второй части планового периода Q2 рас- считывается по формуле (1):

Q 2 =

1 2 ■ D ■ P₂ I ■ C₂

Суммарные издержки, определяемые процессами создания и содержания запасов в течении планового периода продолжительностью T рассчитываются по формуле:

ИО = С, ■ Q, + P + I ■ C, ■ ^ + С₂ ■ (T ■ D - Q,) + 2

(T ■ D - Q , ) ■ yi ■ C 2 ■ P 2

T^d

Таким образом, формулой (3) определяется оптимальный размер партии материала, которую необходимо закупить при наличии достоверного прогноза скачкообразного увеличения стоимости запасаемого материала. Использование МСДМ оказывается актуальным в условиях нестабильной экономики [4].

Определим экономию на издержках управления запасами в плановом периоде при использовании МСДМ в следующих случаях:

– рассматривается скачкообразное возрастание стоимости доставки партии при постоянной цене единицы запасаемого ма- териала;

– скачкообразное возрастание цены единицы запасаемого материала при неизменной стоимости доставки партии.

Первый случай:

Р2=3,-Р1, С2=С1=С. Индекс стоимости доставки партии - 3, (31>1). По формуле

Q* =

I 2 ■ D ■ р

I ■ C

При таком значении раз-

мера партии общие издержки управления запасамиза весь плановый период по формуле (4) составят:

ИО, = 2 ■ Р, + С ■ Т ■ D + 2 ■ T ■ D ■, I ■ C ■ ³ ■ P¹ - 2 ■ _Л/3? ■ P,

^{1          1}                                           2 ■ D                    ^{1    1}

По формуле (3) оптимальный размер партии, закупаемой перед скачкообразным увеличением стоимости определиться следующим образом:

Q * I ² ^ ^D      ^ ^Р ,

• ¹    ■ ^C . Общие издержки по

формуле (4) будут равны:

ИО, = P, ■ (1 + 3,) + C ■ T ■ D + 2 ■ T ■ D ■ I ■ C ■^{3 1} ■ P¹ - 2 ■ 3, ■ P,

2   1      1                                       11

2 ■ D

Экономия за весь плановый период при применении (3) равна:

ИО 1 - ИО 2 = р ■ ! -75 1 ) ² .

Таким образом, при увеличении стоимости доставки партии в 1,5 раза, экономия от применения МСДМ в денежном выражении составит только 5% от первоначальной стоимости доставки независимо от продолжительности планового периода.

При возрастании стоимости доставки в 2

раза, экономия в денежном выражении составит 17% от первоначальной стоимости доставки. Это показывает, что при прогнозировании скачкообразного увеличения стоимости доставки партии и неизменно- сти стоимости единицы запасаемого материала применение МСДМ нецелесообраз- но.

Второй случай:

Р2=Р1=Р, С2=32^С1. Индекс стоимости единицы закупаемого материала  32

(32>1). По формуле (1) оптимальный раз- мер партии запаса равен:

Q* =

2 ■ D ■ P

I ■ C

.

Суммарные издержки за

весь плановый период на создание и содержание запаса по формуле (4) составят:

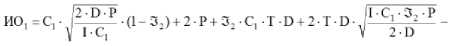
2-р-Тз;

(5.1)

Размер партии запаса, закупаемой перед скачкообразным увеличением стоимости единицы запасаемого материала по формуле (3) составит:

D /        \    1 2 ■ D ■ 3₇ ■ P

Q i * = _T - ⁽ 3 2 - 1 ) + _A    ,   ²

I         v 1 - C1 . Суммарные из держки управления запасом в плановом периоде при использовании МСДМ согласно формуле (4) составят:

ИО 2 = (1 -3 2 ) ■   ² ■ D³* ■ ^P ■ C¹ - 1 ■ C i ■ D ■ ( 3 2 - 1) 2 + P ■ (1

+3₂ ■ C ■ T ■ D + 2 ■ T ■ D ■ . I C ^{1 3 2} P - 2 ■ 3, ■ P

²¹             V  2 ^ D        ²      (5.2)

Таким образом, прогнозируемое скачкообразное изменение цены доставки партии в меньшей степени влияет на размер экономии при использовании МСДМ, чем прогнозируемое скачкообразное изменение цен запасаемого материала. Рассмотрим на примере расчет экономии от использования МСДМ в условиях прогнозируемого существенного увеличения стоимости единицы запасов при разных значениях индекса 3 2 .

Предприятию требуется 1200 кило-

Экономия на издержках управления запасами за весь плановый период за счет применения МСДМ составит:

ио₁ - ио ₂ =

= 1 С 1 . D ( 3 2 - 1 ) ² + ( 1 -3 2 Hi-^ ^J²^ + P4 1 -V3 7 ) ²

• 2       I                                              V I ■ C i

(5.3)

Поскольку 3 ₂>1, все слагаемые в последней формуле положительны, следовательно, применение МСДМ в случае прогнозируемого увеличения стоимости единицы запасаемого материала является целесообразным.

граммов материала в месяц, в настоящее время материал закупается по цене 650 рублей за килограмм. Доставка партии материала стоит 1000 рублей. На содержание запаса уходит 0,1 его стоимости в месяц. Продолжительность планового периода равна одному году. Допустим, стоимость доставки остается неизменной, Р 1 =Р 2 =1000 руб., через 14 дней прогнозируется увеличение стоимости 1 кг материала в 3 ₂ раз. Необходимо определить годовую экономию от применения МСДМ. Результаты расчета годовой экономии от применения МСДМ представлены в таблице 1.

Таблица 1. Расчет экономии от применения МСДМ, при разных значениях индекса стоимости единицы запасов

3 2	С 2 , руб.	Q*, кг рассчитанный по формуле (1)	Q 1 *, кг рассчитанный по формуле (3)	Относительная экономия от применения МСДМ, в %
1,2	780	192,15	2610,49	1,39%
1,3	845	192,15	3819,09	2,90%
1,4	910	192,15	5027,36	4,79%
1,5	975	192,15	6235,34	6,98%
1,6	1040	192,15	7443,06	9,44%
1,7	1105	192,15	8650,54	12,10%
1,8	1170	192,15	9857,80	14,93%
1,9	1235	192,15	11064,87	17,91%
2	1300	192,15	12271,75	21,01%

Для рассматриваемого примера применение при расчете оптимального размера партии МСДМ вместо EOQ целесообразно при скачкообразном увеличении стоимости одного килограмма материала на 30% и более (Таблица 1).

Рассмотрим, как будет зависеть экономия при применении МСДМ вместо EOQ от стоимости хранения запасов. Очевидно, что чем дороже обходится хранение, тем менее выгодно делать запасы, это может быть нецелесообразно даже в условиях роста их стоимости. В предлагаемом примере (таблица 1) при росте стоимости запасаемого материала на 60% (32=1,6), экономия оказывается существенной – 9,44%. Предположим, что хранение запаса материала будет стоить предприятию дороже, иначе, коэффициент пропорциональности издержек содержания I меняется от 0,1 (1/мес.) до 1 (1/мес.). Индекс стоимости единицы запасаемого материала 32=1,6.

Интенсивность расходования материала равна 1200 кг/мес. (таблица 2).

Таблица 2. Зависимость экономии от применения МСДМ от стоимости содержания запасов при индексе закупочной цены ℑ 2 =1,6

I, (1/мес.)	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0
Q1*, кг рассчитанный по формуле (3)	7443,1	3771,9	2540,3	1921,5	1548,7	1299,2	1120,4	985,9	881,0	796,9
Q*, кг рассчитанный по формуле (1)	192,15	135,87	110,94	96,08	85,93	78,45	72,63	67,94	64,05	60,76
Экономия от применения формулы (3)	9,44%	4,71%	3,14%	2,36%	1,89%	1,57%	1,35%	1,18%	1,05%	0,94%

Из анализа формул (5.1), (5.2), (5.3), а также зависимости экономии, возникающей при применении МСДМ, от значений индекса стоимости одной единицы материала, можно определить области целесообразности применения МСДМ.

Для материалов, составляющих высокую долю в себестоимости готовой продукции (примерно 10% всех материальных запасов), применение для определения оптимального размера партии МСДМ вместо EOQ целесообразно уже при увеличении их стоимости на 20%.

Для материалов, имеющих менее существенную долю в себестоимости конечной продукции (приблизительно 25% ассортиментных позиций материалов), применение МСДМ целесообразно в случае увеличения их стоимости на 100% и более.

При разработке системы управления ассортиментными позициями запасов, составляющими наименьшую долю в себестоимости продукции (оставшиеся примерно 65% запасов), нецелесообразно применять МСДМ.

МСДМ не может применяться при высокой стоимости создания условий для хранения увеличившегося размера партии.

МСДМ оказывается актуальной при управлении запасами в условиях нестабильной экономики. Особенно стоит обратить внимание, на прогнозируемые изменения стоимости материалов, связанных с особенностями государственного регулирования экономики, поскольку в этом случае весьма вероятно построение достоверного прогноза.