Анализ устойчивости и вторичных режимов термокапиллярного течения в слое жидкости при локализованном нагреве

В последнее время усилился интерес исследователей к течениям, возникающим в слое жидкости c поверхностью раздела при пространственно-неоднородном нагреве.

Если слой достаточно тонкий, то преобладает термокапиллярный механизм возникновения течения, обусловленный неоднородностью поверхностного натяжения в силу его зависимости от температуры. Такие течения характеризуются не только движением жидкости вдоль свободной поверхности, но и дефомацией самой поверхности [1]. Это явление имеет многочисленные технические приложения. В частности, практическая потребность в количественной оценке интенсивности течения и степени термокапиллярной деформации возникает в процессе лазерной обработки поверхностей в металлургии [2], при выращивании кристаллов методом зонной плавки [3], при разработке рецептов декоративных покрытий в лакокрасочной промышленности, в методиках, использующих явление фотоиндуцированной капиллярной конвекции при разработке жидкослойных систем регистрации информации и способов определения физических свойств тонких слоев жидкости [4] и в других ситуациях.

Термокапиллярное течение и деформация границы, вызванные локализованным нагревом поверхности раздела или приповерхностного слоя жидкости вследствие воздействия сосредоточенного источника тепла, созданного излучением лазера или некогерентного источника света, экспериментально изучались в работах [4-8]. В зависимости от параметров источника излучения и от стадии развития процесса в экспериментах наблюдались различные типы деформации границы раздела вблизи горячего пятна: выпуклый или вогнутый мениск и более сложные конфигурации поверхности с переменной кривизной. Структура конвективного течения, как правило, была одновихревой с радиальным растеканием жидкости от нагретой области.

Похожие и более сложные структуры получались в экспериментах [9], где твердотельный локализованный нагреватель помещался вблизи поверхности в глубине слоя. В этом случае по мере увеличения интенсивности источника или его приближения к поверхности последовательно отмечались стационарные формы поверхности, осцилляции мениска, концентрические и спиральные поверхностные волны.

Подобные режимы течений, вызванные локализованной неоднородностью поверхностного натяжения, и последовательность их бифуркаций наблюдались в лабораторных экспериментах, но не получили пока должного теоретического объяснения и не исследованы средствами численного моделирования. Наиболее полное описание сложного поведения конвективной системы с межфазной поверхностью должно основываться на результатах расчетов развитых трехмерных нелинейных режимов и исследовании их устойчивости. Это частично реализовано в немногочисленных работах лишь для предельного случая недеформируемой границы раздела [2, 10, 11].

Развиваемый в настоящей работе подход предполагает сведение трехмерной задачи к двумерной в рамках амплитудных уравнений длинноволнового приближения [12]. В применении к задаче с неоднородным нагревом этот подход позволяет правильно отразить основные особенности течения и деформации поверхности, наблюдаемые в лабораторных экспериментах с тепловым источником, создаваемым лазером или некогерентным источником излучения [8,13,14], и обладает богатыми возможностями по изучению различных типов граничных условий, форм неоднородности теплового или концентрационного потока и позволяет продвинуться в область существования развитых нелинейных режимов.

Математическая модель, соответствующая этому подходу, представляет собой систему нелинейных дифференциальных уравнений в частных производных для амплитуд температуры, завихренности и деформации поверхности жидкости. Целью работы является параметрическое исследование модели, определение областей параметров, при которых реализуются стационарные решения (стационары) различной структуры, исследование их устойчивости к малым возмущениям и нелинейной эволюции неустойчивых возмущений.

• 2.    Постановка задачи

Рассматривается тонкий горизонтальный слой вязкой несжимаемой жидкости толщиной L , нижняя граница которого считается теплоизолированной, а верхняя — свободной и деформируемой. Предполагается, что в жидкости установлено распределение температуры, соответствующее однородному подогреву снизу. Это поле искажено наложением слабо неоднородного теплового потока (Рис. 1).

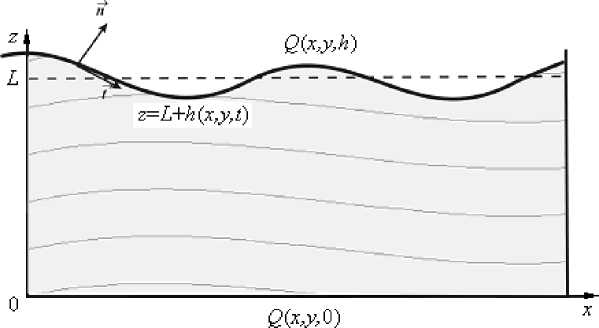
Рис.1. Геометрия задачи

Система уравнений, описывающая конвекцию, в терминах горизонтальной й ( x , y , z , t ) и вертикальной w ( x , y , z , t ) компонент скорости, температуры T ( x , y , z , t ) и давления p ( x , y , z , t ) имеет вид:

P {d tй + (й V) й + wW}=-Vp + A й + й", P { d tw + ( й V ) w + ww '} = - p' + A w + w"- G, V- u + w ' = 0, 5 tT + й -V T + wT ' = A T + T".

Если функцию, характеризующую мощность источника тепла, представить как

Q ( x , y , z ) = q ( x , y ) - q z ( z ) , то граничные условия запишутся в следующем виде:

z = 0: й = w = 0, T ' = - 1 + q ( x , y ) - q z ( 0 ) ;

z =1 + h (x, y): dth + й-V h = w, T '=V h-V T - 1 + q (x, y)-qz (h); qz (1) = Z •

На поверхности z = 1 + h ( x, y ) , где h ( x, y ) — деформация поверхности жидкости, выполняются условия баланса нормальных и тангенциальных компонент плотности потока импульса ^п_л = ^- p b i_k + n ( V i,k + V k,i ) :

П nn =V

V h _v V¹ + ( ^v h ) ²,

( Са - Ma T ) ,

П

nti

= Ma

(

ч V1+(dh)2

(diT + T 'Sih)

Уравнения (1)–(3) и граничные условия (4), (5) записаны в безразмерных переменных с использованием в качестве единиц измерения: длины — L , времени — L 2 /х , скорости — х/ L , давления — nx/ L 2 , температуры — AL , где A — абсолютная величина равновесного градиента температуры. Символы n , v , Х , о обозначают коэффициенты динамической вязкости, кинематической вязкости, температуропроводности и поверхностного натяжения жидкости соответственно. Штрих означает дифференцирование по вертикальной координате z , а операторы V и А cодержат производные только по горизонтальным координатам x и y .

В построенной модели присутствуют следующие безразмерные параметры: число Марангони — Ma = ( 5о/5 T ) QL /( nx ) , число Прандтля — P = v/x , число Галилея — G = gL /( vx ) и капиллярное число — Ca = о L[ ( nx ) • Параметр £ в выражениях (4) характеризует вертикальную тепловую неоднородность, причем Z = 0 означает, что q_z ( z ) = const.

Для удобства дальнейшего изложения проводится переобозначение параметров: c = 72/Ca, 5 = G/Ca, при этом значения c = 0, 5= 0 соответствуют случаю недеформируемой поверхности.

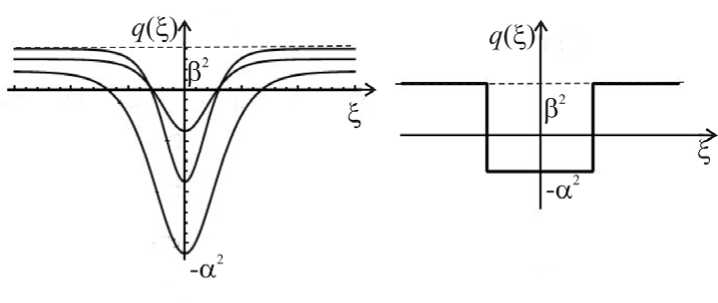
Предполагается, что неоднородный источник тепла локализован в горизонтальной плоскости. В дальнейшем будут рассмотрены два варианта конфигурации теплового пятна: плоское и осесимметричное; тогда функция q ( x , y ), описывающая горизонтальную неоднородность нагрева, будет зависеть от одной пространственной переменной, обозначаемой £ и имеющей разный смысл в зависимости от изучаемой ситуации: q = q ( £ ) , где £ = x соответствует случаю плоского источника, £ = r — случаю осесимметричного источника. Эта зависимость в основных расчетах выбиралась в виде гладкой функции: q ( £ ) = [в 2 ■ sh² ( Р'^ ) -а ² ] /ch² ( р-^ ) ; в ряде случаев также использовалась ступенчатая функция (Рис. 2).

Параметры а и Р функции q ( £ ) характеризуют меру отклонения теплового потока от критического значения, соответствующего порогу возбуждения термокапиллярной конвекции, внутри теплового пятна ( - а ² ) и вне его ( р ²). Параметр R определяет радиус теплового пятна ступенчатой функции теплопотока. Далее в расчетах рассматривается только случай плоской геометрии теплового источника.

а                          б

Рис.2. Гладкая ( а ) и ступенчатая ( б) горизонтальная неоднородность теплопотока q( ^ ) при различных параметрах а , в

• 3.    Длинноволновая аппроксимация

Предполагается, что горизонтальные масштабы термокапиллярного течения, поля температуры и деформации поверхности намного больше, чем вертикальные. Это допущение позволяет применить метод асимптотических разложений, согласно которому переменные, описывающие возмущения, раскладываются в ряд по малому параметру в , связанному с отношением вертикального и горизонтального размеров: 8 2 = ( df /дx )/( 5 f ( ) « 1. В рассматриваемом случае для возмущений скорости, температуры, деформации поверхности и давления можно записать следующие асимптотические разложения:

W — в ( W 0 + В W 1 + В 2 W 2 + ...

T — T ₀ +в T + в ² T 2 + ...,

и — ^В ( и о + В U y + В и 2 + ... ) ,

h — в ( H + в H 1 + ... ) ,       p — в^{- 1} P - 1 + P 0 +в P 1 + ... .

После преобразования масштабов по формулам

(x, у) > д/В" (x, у), t > в't, G > bG, Ca > B2Ca в низших порядках по в (-1 и 0) из выражений (6, 7) получаются соотношения:

P - 1 — G ( 1 - z ) , P ₀ — G H - Ca A H , T ₀ — - z + Ф , U — 12 f ‘ ( z ) VФ , W 0 —- 12 f ( z ) АФ .

Учёт в разложениях (6, 7) членов до второго порядка по в позволяет получить используемую в дальнейшем математическую модель задачи в длинноволновом приближении в виде системы нелинейных дифференциальных уравнений для функций Ф ( x , у ) , Т ( x , у ) и H ( x , у ) , характеризующих изменения амплитуд полей температуры, завихренности и деформации свободной поверхности вблизи критического значения числа Марангони (Ma c — 48):

at ф + VФ•V х (ez т)+115 v4Ф - v2 h - 3| v • (|VФ |2 VФ) + 2V • (н VФ) ++ | — + — |v•(v2ФVф) + ^3 + — |V2 VФ|2 - V-(^Ф) +1V2q +ZqH — 0;

(10 I P J              ⁷ (I 10 P J ^{1 1 V 2} 2

az V2 Т — ;31P' V(v2ф)хVФ-24V H хVФ;                                  (9)5V2H -V4H — - с V2Ф.

Здесь f ( z ) = z ² - z ³; e z — ( 0,0,1 ) .

В случаях плоского и осесимметричного задания тепловой неоднородности система уравнений (9) для основного состояния, зависящего от одной пространственной координаты ^ , не содержит функции Т ( Т = 0). В рассматриваемом далее плоском варианте теплопотока q ( x ) остальные функции удовлетворяют следующей системе уравнений:

—ФоIV (x) - H" (x) - 48 (фо' (x )3) + f13 + —) (Фо ' (x) Фо" (x))' +

15 ^{0            0}          35 \ ⁰      / v 10 5 P J^{3 0}         0 \

+2 (H0 (x) Фо* (x))'-(q (x) Фо* (x))' + 2 q "(x )+Zq (x) H0 (x ) = 0;                 (10)5 H0 (x) + c Ф0 (x) - H0" (x) = 0.

Далее, в терминах этих функций ищутся решения (9), локализованные в окрестности теплового пятна. Граничные условия в этом случае принимают вид: – для плоской задачи:

Ф ( x , t ) > 0, 5 _x Ф ( x , t ) > 0, H ( x , t ) > 0, 5 _xH ( x , t ) > 0 при x >+да ;

– для осесимметричной задачи

Ф ( r , t ) > 0, d _r Ф ( r , t ) > 0, 5 2 Ф ( r , t ) > 0,

H ( r , t ) ^ 0, d r H ( r , t ) ^ 0, d 2 r H ( r , t ) ^ 0,      ^{при r} ^⁺” ,

5 _r Ф ( r , t ) = 0,    5 _rH ( r , t ) = 0                при r = 0 .

• 4.    Методы решения амплитудных уравнений

Для решения амплитудных уравнений (10) применяется метод Галёркина. Наличие бесконечной области определения искомых функций затрудняет численную реализацию этих уравнений. Требуется в качестве базисных выбирать такие функции, которые были бы определены на бесконечном промежутке и удовлетворяли бы граничным условиям. Поскольку ищутся решения, локализованные в окрестности теплового пятна, базисные функции также должны быть локализованы в этой же окрестности и должны стремиться к нулю при бесконечном удалении от неё. На практике реализация такого подхода затруднена вследствие сложного вида базисных функций, удовлетворяющих всем приведённым требованиям, что обуславливает сложность определения интегралов в процедуре проектирования уравнений на базис Галёркина (при вычислении невязок). Последняя может быть реализована в этом случае только численно.

Наиболее перспективным представляется другой путь решения уравнений. Перед тем как непосредственно применить метод Галёркина, следует провести преобразование координат, такое, чтобы искомые функции имели конечную область определения. В качестве такого преобразования выбирается ^ = th ( в • x ) , тогда x е ( ^ , да ) > 2 е [ - 1,1 ] . Преобразование координат влечёт за собой преобразование амплитудных уравнений и граничных условий. Проделанная процедура позволяет использовать базисные функции, определённые на конечном промежутке, в частности полиномы от новой независимой переменной { ^ k } ₀₁₂ . Базисные функции ищутся в виде: Ф ₀ = Х а . '5 k , H 0 = ^bk • 5 ^k .

,k = 0,1,2,...                                                      r                т

Далее, согласно методу Галёркина, эти функции подставляются в преобразованные амплитудные дифференциальные уравнения. Коэффициенты a_k , b_k ( k = 0,1,2,... ) определяются из условия минимума невязки, в результате чего исходные дифференциальные уравнения сводятся к системе нелинейных алгебраических уравнений относительно этих коэффициентов:

• Y ⁰j ⁺ E Y ¹^- • ^ai ⁺ E y ² i , j , k • ^ai • ^ak ⁺ E Y 3 i , j , k , 1 • ^ai • ^ak • a l = ⁰ ( ^j = 0, 1, ², ... ) . ii , k         i , k , l

Здесь у ⁰, Y 1 , Y 2 , Y 3 есть постоянные коэффициенты. К системе добавляются ещё два алгебраических уравнения, следующие из граничных условий. Затем ищутся действительные решения полученной системы, для чего составляется функционал из суммы квадратов левых частей входящих в нее уравнений. С помощью стандартных функций системы Mathematica [15] находится его минимум, который и является искомым решением.

Проведено исследование зависимости решений амплитудных уравнений от числа базисных функций. Результаты представлены на рисунке 3. Видно, что для сходимости решения достаточно 6–8 базисных функций.

Помимо метода Галёркина использовались метод пристрелки и сеточные методы. Их существенным недостатком является то, что возникает необходимость рассмотрения конечной области L определения искомых функций и проведения дополнительного анализа зависимости решений от размера области определения.

На рисунке 4 представлена зависимость значения температуры в центре теплового пятна от L . Важно подчеркнуть, что вид зависимости резко меняется при малом изменении управляющего параметра. Это создаёт дополнительные трудности, так как требуется корректировка размера области при изучении зависимости решения от параметров задачи. В связи с большей простотой реализации и меньшим временем вычислений в качестве основного был выбран метод Галёркина.

Расчёты стационарных решений проводились для широкого диапазона изменений параметров неоднородности теплопотока а и в при фиксированном значении параметра ширины теплового пятна R = 1 и для различных значений физических параметров c , 8 .

Ф(х=0)ч

-0,009 :

-0,010 :          . .........

-о,ои :      •

-0,012       ......,

0   2   4   6    8   10 12 ДГ

Рис.3. Зависимость амплитуды температуры в центре теплового пятна Ф ( x = 0 ) от числа базисных функций N при значениях параметров а = 0,1; в = 0,1; c = 0,001; 8 = 0,001; Pr = 13; Z = 0

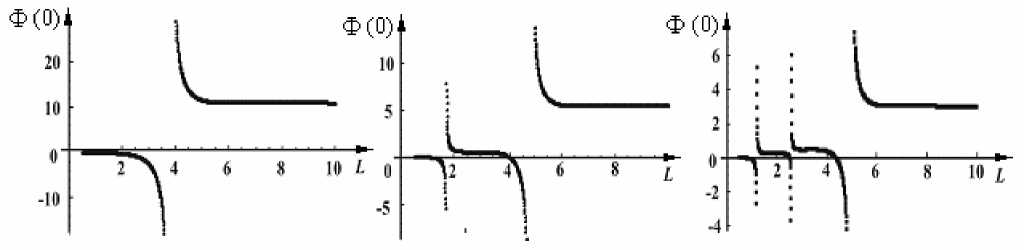
а                              б                              в

Рис.4. Зависимость амплитуды температуры в центре теплового пятна от длины промежутка L (линейная задача, недеформируемая граница, в = 0,3) при следующих значениях параметра неоднородности нагрева а : 0,3 ( а ), 0,5 ( б ), 0,7 ( в )

• 5.    Исследование устойчивости стационарных решений в линейном приближении

Практический интерес представляют не все найденные стационарные решения. Наблюдаться в экспериментах и расчетах полной системы (9) могут лишь те из них, которые обладают устойчивостью по отношению к малым возмущениям. Для выявления этих решений искомые переменные в амплитудных уравнениях представлялись в виде Ф ( x,у, t ) =Ф о ( x ) +Ф ' ( x,y ) • e t , H ( x , y , t ) = H 0 ( x ) + H ' ( x , y ) • e ^Х t , Т ( x , y , t ) = Т ₀ ( x ) +Т ' ( x , y ) • e ^x t . Здесь Ф ₀, H ₀, T ₀ — стационарные состояния, а Ф ', H ', Т ' — малые возмущения. В таком виде искомые функции подставлялись в амплитудные уравнения, в которых сохранялись только слагаемые первого порядка малости относительно возмущений. В результате получалась следующая краевая задача на собственные значения:

ХФ ' + -1- ДДФ ' - — У • (| УФ ₀12 УФ ' ) - — У • ( ( УФ ₀ • УФ ' ) УФ ₀ ) + 2 У • ( H ₀ УФ ' ) + +( 1-0 + -р ^•( ДФ ₀УФ ' + ДФ ' УФ 0 ) + ( - + - р ^Д ( УФ 0 •УФ ’ ) - у • ( q ( x ) УФ ' ) + +Д H ' + 2 У- ( H ' УФ ₀ ) + Z q ( x ) H ' + УФ ₀ •Ух ( у Т ' ) = 0;

—( У ( ДФ ₀ ) хУФ ' +У ( ДФ ' ) хУФ 0 ) - 24 У H ₀ хУФ ' - 24 У H 'хУФ 0 -у ДТ ' = 0;

c ДФ ' + 5Д H ' - ДД H ' = 0 .

Малые возмущения задавались в виде:      Ф ' ( x , y ) = ф ' ( x ) • e^{k -} i " ^{x +} k ² i " ^y ,

H ' ( x , y ) = h ' ( x ) • e k ¹ ^ i • ^{x +} k ² i • ^y , Т ' ( x , y ) = ^ ' ( x ) • e^v i • ^{x +} k ² i • ^y , где Х — декремент возмущений, а k ₁, k ₂ — волновые числа в направлениях x , y . В дальнейшем рассматривались только такие возмущения, для которых k _- = 0. Предполагалось, что возмущения локализованы в окрестности теплового пятна и затухают на бесконечности. Решения, исследуемые на устойчивость, вычислялись для множества значений параметров а и в . С учётом того, что само решение зависит от этих параметров, исследование при фиксированных в проводилось для «ветви» подобных решений. Под «ветвью» понимается множество решений сходной пространственной структуры, вычисленных для различных значений параметра а , когда остальные параметры остаются фиксированными.

Задача исследования устойчивости стационарного состояния системы (9) в линейном приближении сводилась к поиску нетривиальных решений системы линейных однородных обыкновенных дифференциальных уравнений (11). Эта система, как и при нахождении стационарных решений, решалась методом Галёркина с предварительным преобразованием координат ^ = th (в^ x), сводящим бесконечную область определения к конечной. Искомые амплитуды возмущений считались локализованными в окрестности теплового пятна и приближались полиномиальными функциями независимой переменной: ф' =Е a* •^k,h'=Е bk •^k, v'= Е ck • ^k . После подстановки этих функций kkk в преобразованные уравнения для возмущений и минимизации невязки получались линейные алгебраические однородные уравнения относительно неизвестных коэффициентов ak, bk, ck (k = 0,1,2, ...). Таким образом, задача сводилась к алгебраической проблеме собственных значений, которыми являются декременты возмущений. Собственные значения определялись из условия существования нетривиальных решений этой системы. Задача на собственные значения решалась с

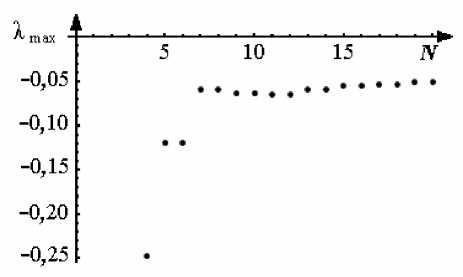
Рис.5. Зависимости максимального значения декремента X max от числа базисных функций N при значениях параметров: а=0,1; в = 0,1; c = 0,001; 5 = 0,001; Pr = 13; Z=-0.015

помощью стандартных функций Eigenvalues, Eigenvectors и Eigensystem системы Mаthematica . Их аргументом являлась квадратная матрица, собственные векторы которой требовалось найти.

Результаты исследования зависимости максимального декремента от числа базисных функций в разложении Галёркина (Рис. 5) демонстрируют, что сходимость наблюдается уже при 8–10 функциях.

• 6.    Результаты расчётов стационарных решений и их исследование на устойчивость

Нелинейные амплитудные уравнения (10) имеют множество решений при конкретных фиксированных параметрах системы. Зависимость полученных в расчетах значений функции амплитуды деформации поверхности в центре теплового пятна от параметра а и соответствующие пространственные структуры искомых функций показаны на рисунке 6, где сплошные линии соответствуют решениям, устойчивым по отношению к одномерным возмущениям (с волновым числом к 2 = 0), а штриховая — неустойчивым к ним.

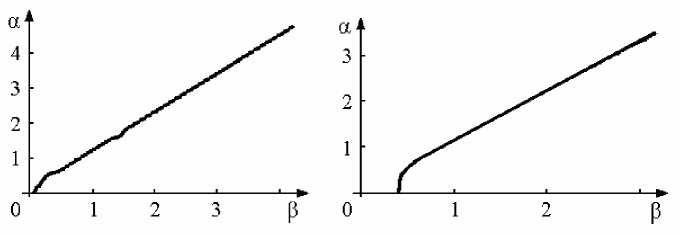
В результате проведенного исследования получены карты устойчивости на плоскости параметров ( а , в ) , характеризующих слабонеоднородный тепловой поток (Рис. 7). Области устойчивости стационарных решений расположены под нейтральной кривой. Обнаружены следующие закономерности: для достаточно малых значений в (меньших некоторого критического значения в * ( c , 5 ) ) основное решение неустойчиво во всей области изменения а , что наблюдается и при линейном анализе устойчивости состояния механического равновесия в упрощенной постановке [13]; в области в>в * ( c , 5 ) при малых значениях параметра а решения устойчивы, но существует критическое значение параметра а _* , при превышении которого решения становятся неустойчивыми для возмущения с определенным значением волнового числа k ₂ , и при дальнейшем росте а область волновых чисел, соответствующих неустойчивым возмущениям, растет; при увеличении параметров с и δ, что соответствует бóльшим деформациям свободной поверхности, область неустойчивости расширяется, при этом значение в * ( c , 5 ) также возрастает (Рис. 7, б ). Каждая изображенная на рисунке 7 нейтральная кривая получена в результате минимизации критического значения а _* при объединении нейтральных кривых для некоторой совокупности «ветвей» стационарных решений, характеризующихся близкими по форме искомыми функциями.

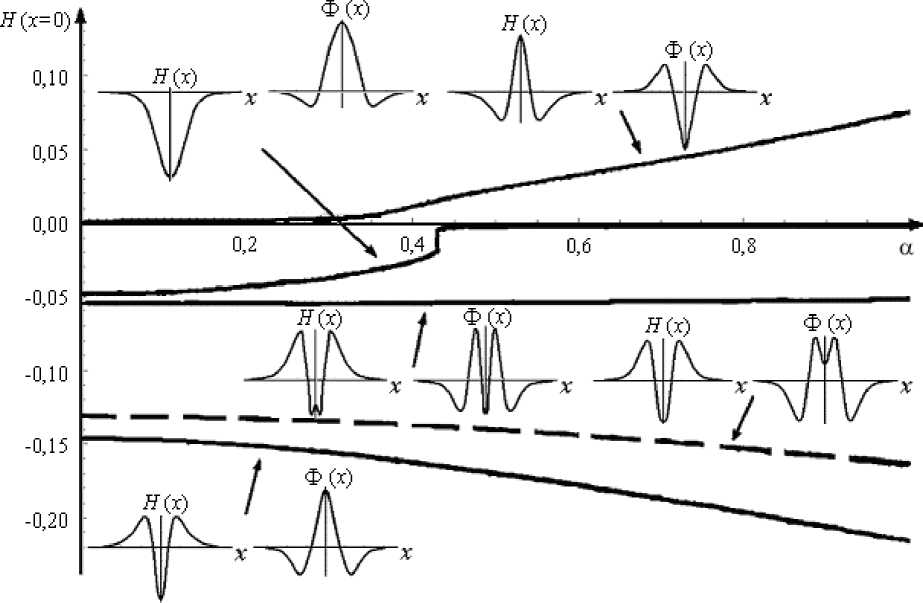
Рис. 6. Зависимость значений функции деформации поверхности в центре теплового пятна от параметра а для плоской задачи при значениях параметров: в = 0,1; с = 1; §=1; Z = -0,015; Pr=13

а                             б

Рис. 7. Нейтральные кривые линейной устойчивости при значениях параметров (Pr = 13; Z = 0): а - c = 0,001, § = 0,001; б - c = 0,1, § = 0,1

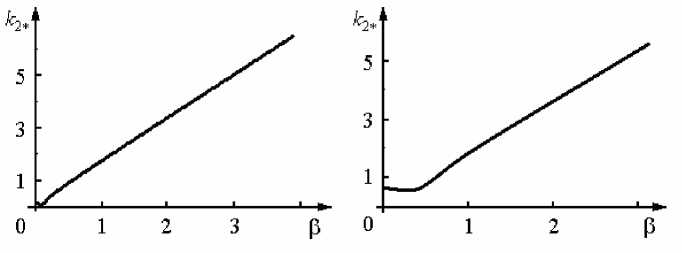
Рис. 8. Зависимость критического волнового числа от параметра в (Pr = 13; Z = 0): а - c = 0,001, § = 0,001; б - c = 0,1, § = 0,1

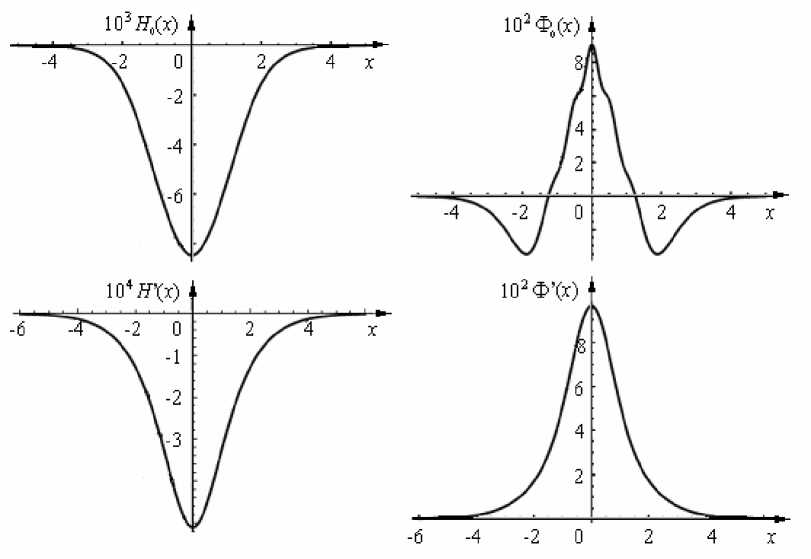
Рис. 9. Пример стационарного состояния H 0 ( x ) , Ф₀ ( x ) с соответствующим критическим возмущением

H ' ( x ) , Ф' ( x ) при значениях параметров а = 2,14; р = 0,6; c = 0,1; 5 = 0,1; Pr = 13; Z = 0

На рисунке 8 показаны зависимости критического волнового числа k _* от параметра в , соответствующие нейтральным кривым рисунка 7. Видно, что при Р<Р * ( c , 5 ) реализуется неустойчивость с волновым числом к ₂ = 0, а при дальнейшем росте в в исследуемом интервале его значений поперечное волновое число имеет тенденцию к росту. На рисунке 9 приведен пример стационарного состояния на нейтральной кривой с соответствующими критическими возмущениями. Из данных примеров видно, что критические возмущения могут иметь симметрию, отличную от основного решения, или быть несимметричными.

• 7.    Численное исследование двумерных амплитудных уравнений

Для анализа устойчивости одномерных стационарных решений и двумерных режимов, развивающихся в результате их неустойчивости, использовалось также численное решение полной двумерной задачи о нелинейном развитии возмущений (9). Задача в полной двумерной нелинейной постановке решена численно на основе полунеявного псевдоспектрального метода, разработанного для задачи с однородным подогревом [16]. Все переменные системы (9) с помощью дискретного преобразования Фурье записывались в спектральном представлении:

N

F ( x , y , t ) = £ F km ( t ) e ^{( kx +} my ) . (12) к , m = 0

Нелинейные конвективные члены в (9) находились путем последовательного вычисления произведений соответствующих переменных в физическом пространстве и обратного перехода в Фурье-пространство. Эволюция Фурье-коэффициентов во времени определялась конечно-разностным методом с использованием схемы дискретизации по

Кранку–Николсону для линейных членов и дискретизации методом Aдамса–Бэшфорта для нелинейных. В качестве начальных условий выбирались либо решения однородной задачи в виде периодических конвективных валов, либо одно из ранее полученных одномерных или двумерных стационарных решений неоднородной задачи.

Проведены расчеты для разного числа Фурье-мод N и различных физических параметров. Выяснено число необходимых Фурье-мод , определяемое характером решения: N = 128. Как следует из проведенных тестовых расчетов, в некоторых случаях это число является недостаточным; в случае появления больших пространственных градиентов решения нужное значение N может превышать 256 функций по каждой горизонтальной координате, что делает актуальным анализ способов повышения эффективности вычислений, например, путем реализации вычислительного алгоритма на компьютерах параллельной архитектуры.

За пределами области устойчивости в зависимости от параметров и интенсивности возмущений в двумерных (2 D ) вычислениях получены локализованные стационарные решения другой симметрии, а также нестационарные решения и глобальные ячеистые структуры (Рис. 10).

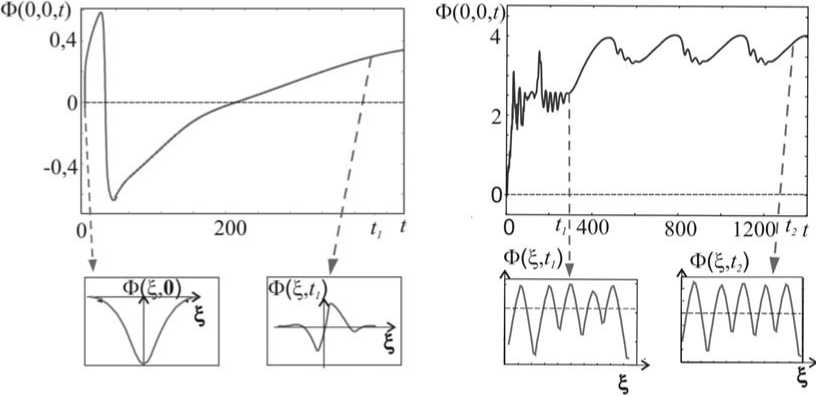
а                                  б

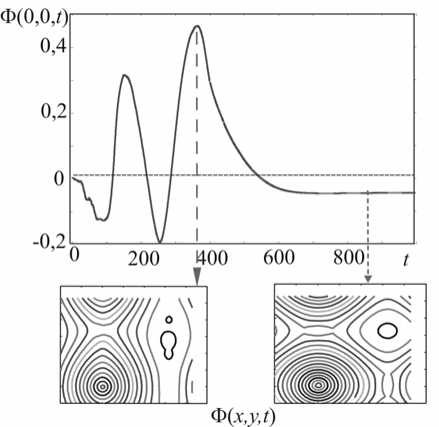
в

Рис.10. Развитие возмущений температуры для разных мод неустойчивости 1 D стационаров: а – 1 D локальная монотонная, б – 1 D глобальная колебательная, в – 2 D глобальная

Работа выполнена при поддержке Российского фонда фундаментальных исследований и Администрации Пермского края (проекты № 07-01-96048_Урал_а, № 07-01-96040_Урал_а).