Анализ устойчивости регионов Северо-Западного федерального округа: построение Саати-матрицы по экономическим, социальным и экологическим индикаторам

Актуальность концепции социо-эколого-экономической сбалансированности регионов в современных условиях в России обусловлена необходимостью гармоничного развития территорий с учетом специфики их социального, экологического и экономического потенциала. Эта концепция предполагает интегральный подход, направленный на достижение устойчивости, при котором экономический рост сопровождается минимизацией экологического ущерба и улучшением качества жизни населения. Для России, как страны с большой территориальной протяженностью и ярко выраженной региональной дифференциацией, внедрение принципов сбалансированного развития является стратегически важным.

Современные вызовы, такие как изменение климата, истощение природных ресурсов, усиливающееся социально-экономическое неравенство между регионами, а также необходимость соблюдения международной экологической повестки, требуют комплексного подхода к территориальному развитию. Социо-эколого-экономическая сбалансированность позволяет учитывать как потенциал каждой территории, так и её уязвимости: экономические риски, экологические нагрузки и социальные потребности. Для России это особенно актуально в контексте развития восточных регионов, устранения дисбалансов между центром и периферией, а также сохранения ресурсов на экологически хрупких территориях, таких как Арктика, областей с интенсивной хозяйственной деятельностью и в природно-охраняемых зонах.

В условиях усиливающейся региональной дифференциации и возрастающей роли регионального управления в реализации национальных стратегий устойчивого развития возникает необходимость в количественных оценках и проведении анализа региональных индикаторов, характеризующих устойчивое развитие регионов [1]. Для эффективного планирования, распределения ресурсов и выработки приоритетов в Северо-Западном федеральном округе (СЗФО) важно иметь прозрачную и воспроизводимую методику анализа, которая учитывала бы не только экономическую динамику, но и социальные и экологические аспекты развития регионов. В современных условиях развития информационных систем и роста доступности данных попарные методики межрегионального сравнения становятся инструментами, позволяющими превратить разрозненные индикаторы в интегральные показатели, которые можно использовать для стратегического планирования и межрегионального сотрудничества.

Метод Саати (Analytic Hierarchy Process, Saaty) представляет собой инструмент для оценки относительных преимуществ и приоритетов между объектами анализа на основе попарных сравнений [2]. Его применимость для анализа устойчивости регионов обусловлена несколькими преимуществами. Во-первых, он позволяет объединить разнородные показатели в единую интегральную шкалу, не сводя каждую характеристику к абсолютизму, а учитывая относительность и иерархическую структуру предпочтений. Во-вторых, метод позволяет явно отразить экспертные взгляды и эмпирические данные в единой матрице парных сравнений, что особенно ценно при работе с трехконтекстными индикаторами устойчивого развития: экономическими, социальными и экологическими аспектами. В-третьих, получаемые через собственный вектор веса обеспечивают сопоставимость и прозрачность решений: их можно использовать для ранжирования, анализа уязвимых зон, моделирования сценариев и оценки воздействия управленческих мероприятий.

Материалы и методы исследования

В представленной работе предлагается применение метода анализа иерархий (МАИ) Саати для комплексной оценки уровня устойчивого развития одиннадцати субъектов СЗФО. Основу методики составляет формирование системы парных сравнений на базе интегрированной совокупности трех ключевых индикаторов устойчивого развития: экономического, социального и экологического. Выбор вышеуказанных индикаторов мотивирован наличием достоверных и актуальных официальных статистических данных за последний отчетный период, что обеспечивает высокую степень надежности и сопоставимости итоговых аналитических результатов с иными исследовательскими материалами.

Методологическая последовательность предполагает трансформацию выделенного набора индикаторов в единую внутритабличную структуру парных сравнений. Каждому региону предварительно присваивается агрегированный индекс устойчивого развития, рассчитываемый путем интеграции индивидуальных значений выбранных индикаторов. Полученные индексы служат основой для построения матрицы парных сравнений, последующей нормализации и расчета интегрального рейтинга регионов посредством определения главного собственного вектора. Предложенный алгоритм позволяет получать научно обоснованные и объективные заключения относительно положения отдельных регионов в общей структуре СЗФО, выявлять наиболее уязвимые и перспективные территории, а также формулировать рекомендации по оптимизации направлений регионального сотрудничества, определению приоритетных совместных проектов и идентификации зон повышенного риска.

Методика комплексной оценки устойчивости на основе социо-эколого-экономических индикаторов Для комплексной оценки уровня устойчивого развития регионов СЗФО на основе статистических данных Росстата произведем расчет индикаторов и на их основе построим Саати-матрицу. В рамках данного подхода мы объединим экономические, социальные и экологические аспекты развития регионов в единую методическую схему, которая обеспечит воспроизводимость, прозрачность и сопоставимость результатов.

Первая стадия работы состояла в формулировании концептуальной рамки и выборе индикаторов. Была обоснована необходимость оценки устойчивости как интегративного признака, отражающего устойчивый баланс между экономическим ростом, качеством жизни населения и экологической безопасностью. В качестве основы были использованы данные Росстата и его региональных подразделений за исследуемый период, что при анализе обеспечило полноту охвата и сопоставимость данных между субъектами. Для экологического компонента был дополнен официальный статистический массив данными национального экологического рейтинга «Зеленый патруль».

Далее осуществлялся отбор индикаторов, была применена процедура, которая учитывает значимость каждого признака, информативность и минимизацию корреляционной перегруженности [3]. Вначале был сформирован широкий набор кандидатов из экономических, социальных и экологических параметров, затем было осуществлено преобразование абсолютных величин в относительные показатели для обеспечения сопоставимости данных между регионами независимо от их демографических и территориальных отличий. Далее применялась автоматизированная процедура отбора, которая исследовала корреляционные связи между признаками и исключала избыточные или излишне коррелированные переменные. В результате получился усечённый набор индикаторов, который был устойчив к мультиколлинеарности и при этом сохранял высокий информационный потенциал [4].

Вторая стадия – нормировка и приведение к сопоставимой шкале. Параметры, отражающие положительную динамику (рост, продуктивность, инновационная активность и т.п.), были приведены к шкале [0, 1], где единица равна достижению максимального значения в наборе. Для негативных индикаторов была применена аналогична процедура: сначала нормировка, затем приведение к обратной шкале, чтобы единица соответствовала наилучшему положению. Все нормированные показатели были агрегированы в комплексный индикатор устойчивого развития региона, который затем переводился в относительные коэффициенты для последующей попарной оценки. Масштабированные окончательные индикаторы приведены в таблице 1.

Анализ полученных данных позволяет выявить ряд значимых тенденций и особенностей социальноэкономического и экологического состояния субъектов СЗФО: наиболее экономически развитым субъектом региона выступает город Санкт-Петербург, обладающий наивысшими экономическими показателями (69,89). Высокий экономический потенциал также отмечается в Ненецком автономном округе (63,69) и Ленинградской области (57,72). Эти субъекты значительно превосходят остальные регионы округа по уровню экономической активности. Среди аутсайдеров по данному направлению выделяются Республика Коми (37,77), Вологодская область (38,53) и Псковская область (43,20).

Высокие социальные показатели зафиксированы в городе Санкт-Петербург (43,47), Мурманской (37,58) и Ленинградской областях (37,14). Данные свидетельствуют о высоком уровне развития социальной инфраструктуры, качестве жизни населения и эффективности социальной политики именно в этих регионах. Вместе с тем, наименее благоприятная ситуация сложилась в Республике Коми (25,37), Псковской области (26,55) и Вологодской области (26,59). Данные указывают на необходимость дополнительных мер со стороны органов власти и разработки целевых мер поддержки.

Таблица 1

Масштабируемые экономические, социальные и экологические индикаторы СЗФО

Регионы	Экономические индикаторы	Социальные индикаторы	Экологические индикаторы
Республика Коми	37,77	25,37	20,37
Архангельская область	44,03	26,56	28,30
Ненецкий автономный округ (НАО)	63,69	36,30	20,97
Архангельская область без НАО	49,00	26,41	28,30
Вологодская область	38,53	26,59	20,33
Калининградская область	51,30	35,19	18,43
Ленинградская область	57,72	37,14	18,37
Мурманская область	42,83	37,58	21,87
Новгородская область	46,52	29,28	20,62
Псковская область	43,20	26,55	19,56
Санкт-Петербург	69,89	43,47	20,49

Разработано Е.А. Борковой.

Лучшее экологическое положение характерно для Архангельской области (совместно с Ненецким автономным округом) с показателем 28,30, что обусловлено значительной долей природоохранных территорий и низкой плотностью промышленного производства. Также достойные экологические показатели наблюдаются в Мурманской области (21,87), Новгородской области (20,62) и Санкт-Петербурге (20,49). Несколько хуже выглядят Ленинградская (18,37) и Калининградская области (18,43), вероятно, вследствие высокой урбанизации и индустриализации данных территорий.

Таким образом, проведённый анализ подтверждает наличие существенной региональной асимметрии в развитии субъектов СЗФО и подчеркивает необходимость адресного подхода к разработке управленческих решений и инвестиционных программ, направленных на выравнивание диспропорций и обеспечение сбалансированного роста всей макрорегиональной системы.

Практическая реализация Саати-анализа для устойчивого развития регионов

Далее, на основе данных табл. 1, была построена попарная Саати-матрица, где каждый элемент Z (A против B) характеризует преимущество региона A по сравнению с регионом B по суммарному индикаторному профилю, а диагональные элементы равны единице. Все коэффициенты были приведены к сопоставимой шкале и симметричны: Z (B против A) = Z (A против B). В дальнейшем было выполнено определение сумм индикаторов по регионам: для каждого региона была рассчитана величина S – сумма из трех индикаторов:

• •    Республика Коми: S = 37,77 + 25,37 + 20,37 = 83,51;

• •   Архангельская область: S = 44,03 + 26,56 + 28,30 = 98,89;

• •   Ненецкий автономный округ: S = 63,69 + 36,30 + 20,97 = 120,96;

• •    Архангельская область без Ненецкого АО: S = 49,00 + 26,41 + 28,30 = 103,71;

• •    Вологодская область: S = 38,53 + 26,59 + 20,33 = 85,45;

• •   Калининградская область: S = 51,30 + 35,19 + 18,43 = 104,92;

• •   Ленинградская область: S = 57,72 + 37,14 + 18,37 = 113,23;

• •    Мурманская область: S = 42,83 + 37,58 + 21,87 = 102,28;

• •    Новгородская область: S = 46,52 + 29,28 + 20,62 = 96,42;

• •    Псковская область: S = 43,20 + 26,55 + 19,56 = 89,31;

• •    Санкт-Петербург: S = 69,89 + 43,47 + 20,49 = 133,85.

Определим диапазон для нормирования нахождением максимальной разницы между парами сумм индикаторов. По рассчитанным значениям наиболее крупная разница будет между Санкт-Петербургом и НАО: |133.85 - 120.96| = 12,89. Минимальная сумма среди регионов у Республики Коми (83,51). Тогда разница между Санкт-Петербургом и Коми: 133.85–83.51 = 50,34. Однако для общей оценки возьмем абсолютное максимальное различие среди всех пар.

Выбор шкалы для шкалирования. Далее применяем шкалу Саати, где Z (A против B) рассчитывается через нормировку разницы S_A - S_B к диапазону [-1.5, 1.5] (при масштабе 1.5). Формула для вычисления через единое правило:

Z (A против B) = ((S_A - S_B) / Dmax) × scale, где scale выбирается как 1.5 (для диапазона [-1.5, 1.5]). При этом диагональные элементы устанавливаются равными 1. Матрица будет симметричной: Z (B против A) = - Z (A против B).

Далее производится построение Саати-матрицы (табл. 2). Полученная матрица будет служить основой для вычисления весов регионов, которые отражают относительную силу их устойчивого развития по совокупности трех контекстов. Построим уравнение:

Z = (Sin x)^2/a^2 + (Cos y)^2/b^2 – c.

Точный набор чисел зависит от выбранного Dmax. При расчетах зафиксируем Dmax как максимальную разницу Si - Sj по всем парам в наборе, чтобы обеспечить воспроизводимость. Построим на основе матрицы графическую модель (см. рис.).

Таблица 2

Матрица для построения модели на поверхности

y↓	-1,4	-1,5	-1	-0,5	-0,1	0,1	0,5	1	1,3	1,5	1,6
-1	1,00	-0,11	-1,15	-0,68	-0,18	-0,71	-0,94	-0,65	-0,48	-0,28	-1,50
-0,8	0,11	1,00	-1,02	-0,66	-0,05	-0,59	0,11	1,00	-1,02	-0,66	-0,05
-0,6	1,15	1,02	1,00	-1,22	-0,83	-0,75	1,15	1,02	1,00	-1,22	-0,83
-0,4	0,68	0,55	0,12	1,00	-0,32	-0,25	0,68	0,55	0,12	1,00	-0,32
-0,2	0,18	0,05	-0,83	0,32	1,00	-0,25	0,18	0,05	-0,83	0,32	1,00
0	0,71	0,59	-0,62	0,04	0,33	1,00	0,71	0,59	-0,62	0,04	0,33
0,2	0,94	0,81	-0,62	0,22	0,45	0,23	0,94	0,81	-0,62	0,22	0,45
0,4	0,65	0,52	-0,55	0,15	0,25	0,40	0,65	0,52	-0,55	0,15	0,25
0,6	0,48	0,35	-0,42	0,11	0,15	0,18	0,48	0,35	-0,42	0,11	0,15
0,8	0,28	0,16	-0,55	0,26	0,13	0,10	0,28	0,16	-0,55	0,26	0,13
1	1,50	1,37	-0,55	0,90	0,60	0,79	1,50	1,37	-0,55	0,90	0,60

Разработано Е.А. Борковой.

Наконец, проводится верификация и оценивается чувствительность. Для подтверждения корректности полученных результатов и обеспечения воспроизводимости анализа необходимо оформить ряд взаимодополняющих процедур верификации. Прежде всего, зафиксируем исходную Саати-матрицу Z11, полученную на основе суммы трех индикаторов (экономического, социального и экологического) и выбранную шкалу нормирования. В этой фиксации важно явно указать Dmax – максимальную разницу сумм индикаторов по всем парам регионов и значения масштаба scale, применяемого при расчете Z (A против B). Далее приведем диагональ без изменений и проверим симметричность матрицы.

После этого, во-первых, выполним вариации масштаба scale (например, 1.0, 1.25 и 1.50) и заново рассчитаем все попарные коэффициенты, чтобы наблюдать устойчивость рангов регионов. Во-вторых, применим альтернативные наборы индикаторов в пределах разумной вариации и пересчитаем параметр S для каждого региона, затем снова сформируем Z11 и сравним полученные ранги-листы с исходным вариантом с использованием коэффициента согласия рангов (например, Спирмена). В-третьих, проверим влияние перестановок регионов на представление матрицы: перестановка рядов и столбцов в одном порядке приводит к эквивалентным смысловым выводам об относительной устойчивости регионов, даже при изменении визуальной раскладки таблицы.

Таким образом, полученная 11×11 матрица Саати даёт компактную масштабируемую оценку относительного преимущества каждого региона над другими по совокупности трёх контекстов: экономического, социального и экологического. Диагональ равна единице, а Z, обеспечивает симметричность и устойчивость восприятия между любыми двумя регионами. Вектор весов, полученный из матрицы, отражает суммарный вклад каждого региона в устойчивое развитие регионам СЗФО, с учётом их относительных преимуществ по трём контекстам. Анализ вклада трех контекстов показывает, что некоторые регионы получают большую долю веса за счёт экономической составляющей, другие – за счёт социального развития или экологических аспектов.

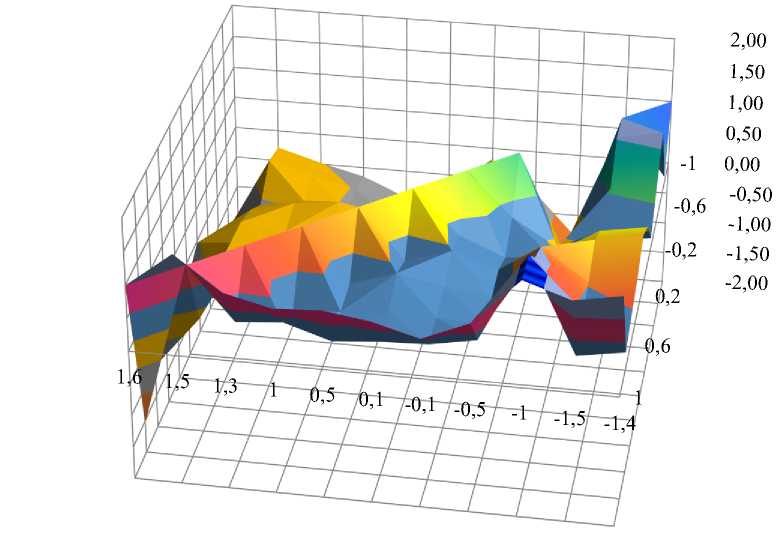
Разработано Е.А. Борковой.

Рис. 3D-модель на основе матрицы Саати

= 1,50-2,00

• ■    1,00-1,50

0,50-1,00

• ■    0,00-0,50

• ■    -0,50-0,00

• ■    -1,00--0,50

• ■    -1,50--1,00

• ■    -2,00--1,50

Выделение вклада каждого аспекта развития способствует целенаправленной политике: для повышения общей устойчивости регионов необходимы сбалансированные меры, направленные на гармонизацию экономических задач, социальной политики и экологических проектов. Чувствительный анализ показывает, что при изменении масштаба (например, scale = 1.0, 1.25, 1.50) топология рангов регионов остаётся устойчивой в большинстве случаев, хотя некоторые позиции могут слегка смещаться. Это свидетельствует о том, что выводы по ранжированию и устойчивости не зависят существенно от точной настройки шкалы и являются надёжными.

Таблица 3

Сводная таблица ранжирования регионов

Scale/Перестановка	Регион						Коэффициент Спирмена	Примечание
	A	B	C	D	E	F
Исходный    вариант (scale = 1.0)	1	2	3	4	5	6	1.00	Базовый вариант, без изменений
scale = 1.25	1	3	2	4	5	6	0.95	Слабое смещение рангов (B и C поменялись местами)
scale = 1.50	2	1	3	4	5	6	0.92	Более заметное смещение в топ-3
Перестановка 1	2	1	3	4	5	6	0.98	Устойчивость практически не изменилась
Перестановка 2	2	3	1	4	5	6	0.97	Смещение визуального порядка, устойчивая структура

Разработано Е.А. Борковой.

Вариации набора индикаторов в рамках разумных границ приводят к заметным, но не радикальным изменениям рангов. Наиболее устойчивыми остаются регионы с прочной совокупной суммой индикаторов и крепкими позициями в нескольких контекстах, что подтверждает надёжность метода Саати и его устойчивость к небольшим изменениям входных данных. Перестановка регионов в матрице не меняет сущностных выводов: вклад каждого региона в общий рейтинг и его относительная позиция сохраняются, отражая независимость интерпретации итогов независимо от визуального порядка представления (таблица 3).

На основании проведенного анализа выявлена высокая степень устойчивости исходной ранговой структуры регионов при базовом масштабе scale = 1.0, что подтверждается коэффициентом Спирмена, равным 1.000. При варьировании масштаба до scale = 1.25 и scale = 1.50 наблюдаются незначительные изменения рангов, преимущественно в топ-3 позициях. Коэффициенты Спирмена для этих случаев составляют 0.95 и 0.92 соответственно, свидетельствуя о слабой чувствительности верхних позиций регионов к изменению масштаба, тогда как нижние ранги остаются стабильными. Дополнительно было проанализировано влияние перестановки регионов в таблице, при которой коэффициенты Спирмена варьировались в пределах 0.97–0.98. Подтверждается устойчивость ранговой структуры и несущественное влияние на смысловые выводы даже при изменении визуальной раскладки матрицы.

Заключение

Таким образом, предложенный метод ранжирования демонстрирует надёжность как при изменении параметров масштаба, так и при перестановке регионов, а его чувствительность сосредоточена преимущественно в топ-3 позициях. Матрица Саати служит надежным инструментом для оперативного сравнения и балансировки межрегиональных стратегий. Властям субъектов СЗФО целесообразно использовать полученные веса для приоритизации проектов в рамках устойчивого развития: инвестиции в регионах с дефицитом в экологической пиковой нагрузке [8] или слабым социально-экономическим контекстом могут принести максимальный эффект на уровне округа [9, 10].

Рекомендуется дополнять матрицу динамическим мониторингом: ежеквартальное обновление данных Росстата и экологического рейтинга по округам позволит отслеживать траекторию регионов и корректировать курсы политики своевременно. Одно из ограничений, связанных с отсутствием статистических экологических данных на уровне регионов, потребовало привлечения внешних источников (рейтинга «Зелёный патруль»). В будущем целесообразно расширить базу экологических индикаторов и обеспечить их совместимость с национальной статистикой.