Анализ влияния окружающей среды на эффективность алгоритма обработки информации в беспроводных сенсорных сетях

В настоящее время в связи с мировыми тенденциями роста стоимости энергии, повышением эффективности и экологичности производства, обеспечением безопасности человеческой и природной жизни уделяется большое внимание разработке и применению инновационных технологий, в том числе беспроводных сенсорных систем. Беспроводная сенсорная система (БСС) – это распределенная, самоорганизующаяся система множества сенсоров, предназначенных для отслеживания физических явлений или условий окружающей среды, а также исполнительных устройств, объединенных между собой радиоканалом [1]. Благодаря своей высокой гибкости, расширенному охвату наблюдения, надежности, мобильности и экономической эффективности, БСС (WSN) имеют широкое применение и высокий потенциал в области военного наблюдения, безопасности, мониторинга окружающей среды [2; 3].

В частности, примером подобной БСС может служить распределенная система охраны. Решения о наличии или отсутствии проникновения на охраняемые объекты в таких системах могут выноситься одновременно несколькими сенсорами по имеющемуся определенному алгоритму. Эти решения далее по радиоканалу передаются в центральный узел (ЦУ), в котором локальные решения, принятые в виде бинарной информации типа «да» или «нет», комплексируются, и выносится окончательное решение о наличии или отсутствии проникновения на объект с целью повышения эффективности. Существенное повышение эффективности по сравнению с эффективностью отдельных сенсоров за счет комплексирования информации в ЦУ показано во многих ранее опубликованных работах [4–8]. Важно отметить, что при функционировании БСС окружающая среда также является одним из элементов, который непосредственно оказывает влияние на эффективность как локальных сенсоров, так и всей системы. В связи с этим цель данной работы заключается в синтезе комплексной системы обнаружения на основе информации от локальных сенсоров, в анализе эффективности принятия решения такой комплексной системой с учетом влияния среды распространения.

1. Влияние окружающей среды на функционирование локального сенсора

В распределенной системе охраны возможно применение датчиков (сенсоров), функционирование которых основывается на разных физических явлениях (звуковом, вибрационном, тепловом излучениях и пр.), причем могут использоваться несколько сенсоров разного типа, обладающих разной эффективностью. Под сенсором будем понимать устройство, преобразующее входное

BSB^ei © Парфенов В.И., Ле В.Д., 2020

Таблица 1

Table 1

Тип среды	Частота	ц / f 2, см - 1 ■ с2
Воздух	132–400 (кГц)	2,94 ■ 10 - 13-3,99 ■ 10 - 13
Кислород	598,9 (кГц)	1,68 ■ 10 - 13 (давление 0,99 атм.)
Углекислый газ	304,4 (кГц)	27,1 ■ 10 - 13 (давление 0,98 атм.)
Вода	7–250 (МГц)	25 ■ 10 - 17 ( t 0 = 20 ° C)

воздействие любой физической природы (температуры, давления, силы света и пр.) в сигнал, удобный для дальнейшего использования. Кроме того, каждый локальный узел содержит не только измерительный сенсор, но и встроенный передатчик, который передает информацию об объекте наблюдения в ЦУ, в котором и реализуется ком-плексирование принятых данных, и выносится окончательное решение. Очевидно, в таких распределенных системах большое внимание необходимо уделять функционированию локального сенсора, который непосредственно воспринимает входные воздействия от объекта и выполняет их первичную обработку. При этом на эффективность принятия решения сенсором будут оказывать непосредственное влияние характеристики окружающей среды распространения. Рассмотрим подробнее примеры влияния окружающей среды на эффективность функционирования подобных распределенных систем охраны.

Практически всегда функционирование измерительного сенсора прямого действия основано на восприятии физических явлений, позволяющих в ответ на неэлектрические воздействия получать на выходе электрические сигналы. К таким явлениям относятся, например, фотоэффект, пьезоэлектрический эффект, эффект Зеебека (термоэлектрический эффект) и др. Известно, что энергия преобразованного электрического сигнала пропорциональна порции излученной энергии от цели. Для описания энергетической характеристики цели может быть использована некоторая физическая величина, эквивалентная излученной мощности от цели. При этом можно записать следующее выражение для интенсивности принимаемого сигнала в открытом пространстве в общем виде [9]:

P

I = —07 exp ( - 2 ц r ) ,                               (1)

4 n r ²

где P0 – излучаемая мощность от источника; ц - коэффициент поглощения, зависящий от частоты излучения и свойств среды. Последний коэффициент может быть получен по расчетными формулам или из справочных материалов. Например, при распространении звука формула для коэффициента поглощения имеет следующий вид [9]:

to 4

ц = —г -n+£+x 2 р v ³ ( ³

где to - частота звукового излучения; р - плот- ность среды; v – скорость распространения волны в среде; n - коэффициент внутреннего трения; Z - коэффициент вязкости; x - коэффициент теплопроводности среды; CV, CP – удельные тепловые емкости при постоянном объеме и давлении; цр - коэффициент поглощения, связанный с релаксацией [9].

Значения нормированного коэффициента поглощения звука для нескольких условий приведены в табл. 1.

В случае распространения вибрации в среде коэффициент поглощения можно определить из следующего выражения [10]:

ц = 4,34 ton v

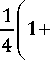
Р 2 v 2 I

Р 1 v 1 )

где to - частота вибрации; n - коэффициент потерь; v – скорость распространения волны; р - плотность среды (предполагается, что вибрация проходит от слоя с индексом «1» к среде с индексом «2»). Значения n , ^v и плотность р для основных типов грунта приведены в табл. 2.

Известно, что мощность полученного сигнала в локальном сенсоре P_c пропорциональна интенсивности звука в данной точке приема. Следовательно, можно записать следующее выражение для мощности полученного сенсором от цели сигнала:

P

Pc = к —02- exp ( - 2 ц r ) ,                              (4)

4 п r ²

где k – некоторый коэффициент пропорциональности.

Таблица 2

Table 2

Вид среды	Плотность среды p , г/см 3	Скорость распространения продольной волны v , м/с	Коэффициент потерь n
Скальный грунт	2,65	3500	0,01
Песок	1,6	600	0,1
Глина	1,7	1500	0,2

2. Алгоритм обнаружения цели

Рассмотрим наблюдение в i-м локальном сенсоре. Для этого введем в рассмотрение гипотезу H1, которая означает, что проникновение на наблюдаемый объект происходит, и гипотезу H0, при выполнении которой такого проникновения на объект нет. Далее будем характеризовать эффективность обнаружения сенсором вероятностями ложной тревоги ai и пропуска цели вi. В практических условиях применений БСС на локальном сенсоре часто используется критерий обнаружения Неймана - Пирсона, поэтому ai часто предполагаются заданными. В то же время вероятность пропуска цели вi зависит от энергии сигнала, полученной от цели. В случае энергетического обнаружения в i-м локальном сенсоре (при расстоянии ri от i-й цели до сенсора) эти вероятности можно найти в соответствии со следующими выражениями:

ai = 1 -Ф( H),   в i =Ф( H — Z (ri)), где

если i -й сенсор обнаруживает проникновение на охраняемый объект; u_i = –1 – в противном случае ( i = 1… K ). Аналогично обозначим через U_i решение, выносимое центральным узлом, в результате обработки сигнала, пришедшего от i -го сенсора. Это решение также может принимать одно из двух значений: U_i = 1, если в ЦУ на основании принятого сигнала выносится решение, что сенсор обнаружил проникновение на охраняемый объект, и U_i = –1 – в противном случае. Кроме того, радиоканал между i -м сенсором и ЦУ будем характеризовать вероятностями ошибок первого и второго рода A_i и B_i .

В [7; 8] показано, как на основе алгоритма ком-плексирования информации в ЦУ может выноситься окончательное решение о наличии или отсутствии цели. По аналогии с [7; 8] выражение для отношения правдоподобия запишем в следующем виде:

KK

M = E c i и Ui = Z X i ( ^Ui ) , i = 1                 i = 1

x

Ф ( x ) = j

-да

exp

V 2 п

-x2L'

dx

– интеграл вероятности;

Z ( r i ) = 2^

– отношение сигнал/шум; H – порог обнаружения;

N – двусторонний спектр мощности белого шума.

Используя формулу (4), можно записать выражение для отношения сигнал/шум для i -го локального сенсора в сокращенном виде как

Z () ! q 2 i exp^{( -} 2 , i r ) ,                                  (6)

^{i                  r}i ²

где q _{0 i} – отношение сигнал/шум при нулевом расстоянии от цели до сенсора.

Решения, выносимые локальным сенсором о наличии или отсутствии цели, могут быть представлены в виде бинарной информации: u_i = 1,

и

v i 0 ’ = ^a i ^{( 1 -B} i ) + ^{( 1 -a} i ^{) A} i , V i 1) = ( 1 — в i ) (1 — В i ) + в i A i .

Следовательно, окончательное решающее правило обнаружения, используемое в ЦУ, можно записать как

K

H ₁

M = E X i ( ^Ui ) > h , i = 1         <

H ₀

где пороговое значение h определяется, исходя из выбранного критерия оптимальности.

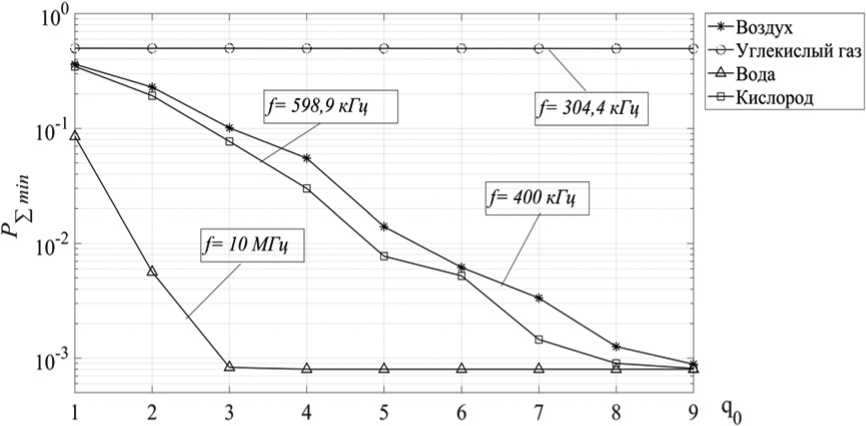
Рис. 1. Зависимость полной вероятности ошибки от энергетического параметра q ₀ для БСС звукового вида

Fig. 1. Dependence of the total error probability on the energy parameter q ₀ for a sound-type wireless sensor system

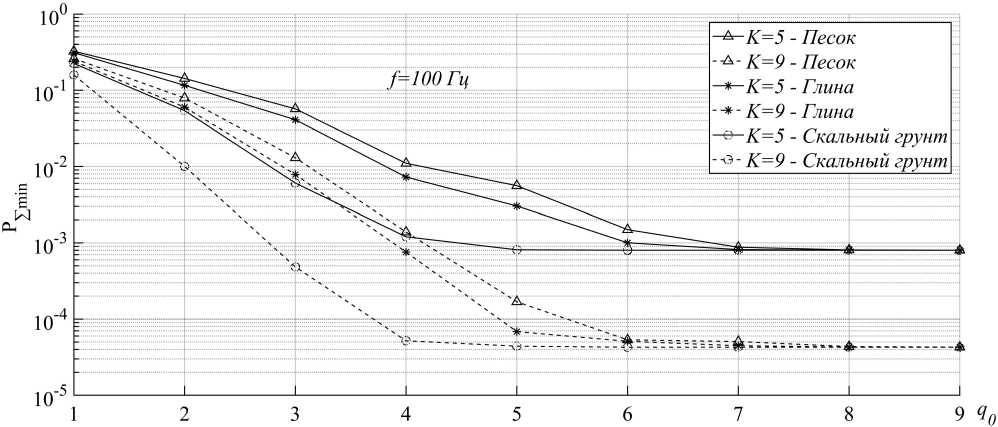
Рис. 2. Зависимость полной вероятности ошибки от энергетического параметра q ₀ для БСС вибрационного вида

Fig. 2. Dependence of the total error probability on the energy parameter q ₀ for the vibration type wireless sensor system

Кроме того, для анализа влияния среды на эффективность системы для простоты предполагалось, что расстояние от цели до каждого локального сенсора одинаково. Для характеристики эффективности алгоритма (8) выберем критерий минимума полной вероятности ошибки P y _min = = min( A y + В y )/2, достигаемого при определенном значении порога h , где Л ^ и В ^ - вероятности ошибок первого и второго рода всей системы соответственно, которые можно определить по полученным выражениям из [7; 8]:

Л ^= 1 -¥()(h *), B^-T ^С h \ причем

W i ⁾⁽ h ’) -« ki ¹ V £ 1 ( h • - C l _t ) +

+ (1 Ч")'1' k-1 (h * + C2 k) • г - 0 или 1; k - 1,...K, Tg)(h ) - n(h ), где q(.) - функция единичного скачка.

3.    Результаты расчетов

В соответствии с вышеизложенным предположим, что вероятности ошибок первого рода для всех сенсоров одинаковы: а ^ - 0,1. Для описания эффективности каналов связи также предположим, что вероятности ошибок первого и второго рода для всех радиоканалов одинаковы и равны A i - 0,01; B i - 0,01.

Полученные результаты расчетов представлены на рис. 1, 2. На рис. 1 приведены зависимости пол- ной вероятности ошибки от энергетического параметра q0 для случая применения БСС звукового вида с количеством сенсором K = 5 и при расстоянии от цели до локальных сенсоров r = 0,3 м.

Из рис. 1 следует, что среда распространения существенно влияет на эффективность принятия решения всей системой. В среде, состоящей полностью из углекислого газа, полная вероятность ошибки всей системы практически не меняется и равна 0,5 (даже при больших значениях ОСШ q о ) (изображена линией с кружочками). В этом случае обоснованное вынесение решений невозможно. Действительно, при этом на уровне локального сенсора звук сильно поглощается средой, что приводит к ухудшению эффективности принятия решения как одиночным сенсором, так и всей системой. Наименьшую степень влияния на эффективность системы оказывает водная среда (вероятность на рис. 1 изображена линией с треугольниками). Однако с ростом энергетического параметра q q (ОСШ) полная вероятность ошибки быстро уменьшается и достигает предельного значения, которое не изменяется даже при увеличении q q . В воздухе и в кислороде влияние среды на эффективность системы более сильное, и в этих двух средах вероятности ошибок практически мало отличаются друг от друга.

На рис. 2 приведены зависимости полной вероятности ошибки от энергетического параметра q ₀ для случая применения БСС вибрационного вида с количеством сенсором K = 5 (сплошные линии) и K = 9 (пунктирные линии) при расстоянии от наблюдаемой цели до локальных сенсоров r = 1 м.

Из рис. 2 следует, что эффективность принятия решения системой в случае применения сенсоров вибрационного вида наихудшая при распростра- нении в песке (верхние линии с треугольниками) по сравнению с остальными видами сред. Наименьшая степень влияния на эффективность всей системы наблюдается в скальном грунте. Кроме того, можно отметить, что эффективность принятия решения системой может быть существенно повышена за счет увеличения количества сенсоров (например, при увеличении количества сенсоров с 5 до 9 вероятность ошибки уменьшается более чем на порядок при не очень малых значениях параметра qq ). Как и в случае звука, при одном и том же количестве сенсоров с ростом энергетического параметра q0 полная вероятность ошибки уменьшается лишь до определенного предела. Это можно объяснить тем, что при больших значениях qо вероятности пропуска цели локальными сенсорами стремятся к нулю, в результате полная вероятность ошибки всей системы практически не меняется с ростом энергетического параметра qq . В этом случае эффективность системы не может дальше повышаться за счет энергетики.

Заключение

В данной работе были выполнены статистический синтез и анализ алгоритма комплексиро-вания информации в беспроводных сенсорных сетях с учетом особенностей среды распространения. Приведенные результаты позволяют оценить эффективность принятия решения системой в разных средах функционирования локальных сенсоров и предварительно выбрать тип сенсора для повышения качества работы системы. Дальнейшим направлением исследований может стать разработка алгоритмов комплексирования информации с учетом замираний в канале связи.