Анализ влияния параметров на движение роботизированных транспортных платформ

Введение. В последние десятилетия значительный прогресс в области робототехники и автоматизации привел к широкому внедрению роботизированных транспортных платформ в различные сферы промышленности и логистики [1]. Эти платформы предназначены для выполнения различных задач, включая транспортировку грузов на производственных предприятиях, складских комплексах и логистических центрах [5]. Одним из ключевых аспектов эффективности роботизированных платформ является их способность к безопасному и быстрому перемещению в динамичной и изменяющейся среде, что требует точного учета различных параметров, таких как коэффициент трения, масса платформы и ее ориентация в пространстве [6]. Актуальность исследования обусловлена необходимостью повышения точности управления и надежности эксплуатации таких платформ [2, 7]. Основная цель работы - разработка математической модели, позволяющей определить движущую силу в зависимости от условий движения и характеристик поверхности. Результаты данного исследования могут быть полезны для разработчиков роботизированных систем, инженеров и специалистов по логистике, стремящихся улучшить производительность и надежность автоматизированных транспортных средств. Понимание взаимосвязи между параметрами движения и их влияние на поведение платформы позволит создавать более адаптивные и устойчивые системы, способные эффективно работать в различных условиях и справляться с непредвиденными ситуациями.

Материалы и методы. В работе применялся литературный обзор, методы инженерного эксперимента, изобретательской деятельности.

Результаты и обсуждение.

Введем обозначения:

• •    F – движущая сила, Н;

• •      Ртр - сила трения, Н;

• •    N – сила реакции опоры, Н;

• •    m – масса платформы, кг;

• •    g – ускорение свободного падения, м/с;

• •    α – угол склона, град;

• •    μ – коэффициент трения;

• •    а - ускорение движения платформы, м/с^2.

Составим систему уравнений согласно второму закону Ньютона [4]:

г F + Ftp + N + Ft = та

t N + Ft = 0

Введем систему прямоугольных координат, в которой ось Ох параллельна силе подъема, а ось Оу–параллельна направлению силы реакции опоры. Переходя к скалярной форме посредством нахождения проекций на оси этой системы, и добавляя в систему соотношение силы реакции опоры и силы трения, запишем:

! F — Ftp — mg • sina = та N — mg • cosa = 0

Ftp = pN

Перенесем слагаемые mg∙sinα и mg∙cosα в правые части первых двух уравнений и представим силу реакции опоры в третьем уравнении произведением mg^ cosa. Заменим Frp в первом уравнении системы на произведение µmg∙cosα из ее третьего уравнения:

!F

- pmg • cosa = mg • sina + та N = mg • cosa        ,

F_Tp = pmg • cosa

При помощи формулы 3 мы можем посчитать движущую силу роботизированной платформы, для этого необходимо знать ее значение ускорения. Так как роботизированная тележка перемещается по той же траектории, что и впереди идущий человек, то ее скорость напрямую зависит от средней скорости перемещения человека.

Рассмотрим случай, когда скорость роботизированной платформы и средняя скорость перемещения человека приблизительно равны и постоянны, то есть они движутся равномерно и параллельно относительно друг друга, тогда:

vp«v4,p = 1,39 м,(4)

vk = const, а = 0 ^2,(5)

F = FTp + mg • sina,(6)

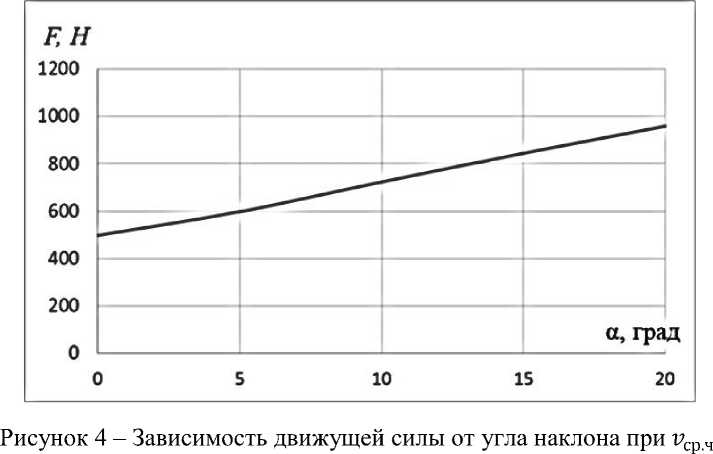
Произведем расчет по 3 формуле, воспользовавшись следующими исходными данными: m = 150 кг; g = 10 ^2; g = 0,25 [3]. Подсчитаем значения движущейся силы при значениях угла наклона от 0° до 20°. Составим таблицу (таблица 1) и построим график (рисунок 1).

Таблица 1 - Зависимость силы подъема от угла наклона при v_p ~ г_ч . _с р

α, град	0	5	10	15	20
F , Н	300	429,6	555,9	678,1	794,9

Рисунок 1 - Зависимость подъемный силы от угла наклона при v_p ~ г_ср . _ч

По данному графику видно, что чем больше угол наклона, тем больше движущая сила, следовательно, при возрастании угла наклона требуется прикладывать большую движущую силу, чтобы преодолеть силу тяжести и силу трения, действующие на роботизированную платформу.

Найдем среднюю скорость человека по следующей формуле:

^{V c}p   t ,

Узнаем допустимое значение средней скорости роботизированной платформы относительно средней скорости перемещения человека на отрезке ab равном 100 м.

км 1000•5 м

^сря = 5 — = 3600 = 1,39 с,

Выразим из приведенной выше формулы время, затрачиваемое человеком, чтобы пройти путь длиной 100 м:

$ _ 100 _ t v_cp 1,39 = ⁷² c,

Рассмотрим случай, когда средняя скорость перемещения человека и скорость роботизированной платформы неравны друг другу и средняя скорость роботизированной платформы изменяется в процессе передвижения, то есть она приобретает ускорение. Зададимся, что ускорение роботизированной платформы величина постоянная и вид его движения равноускоренный:

^р ^ ^ср.ч^ср.ч I,39 ~ (8)

Зададимся условиями, что время на преодоление расстояния от а до b составит 72 с и S1 – расстояние между человеком и роботизированной платформой составляет 5 м, тогда найдем оставшееся расстояние S2, которое необходимо преодолеть роботизированной платформе (рисунок 2).

Рисунок 2 – Перемещение роботизированной платформы и человека на плоскости

S2 = S-S1 = 95 м,

Тогда при заданном времени и пути, найдем среднюю скорость передвижения роботизированной платформы:

vcp = 95 = 1,3 м, ср 72         с

Следовательно, найдём ускорение. Так как движение равноускоренное, то:

= ^к- ^ t , где тк - конечная скорость роботизированной платформы, равная 1,3м,

Тогда:

Vk

а =   , t откуда, а = 1,3 —, при t = 1с - время разгона двигателя.

Тогда найдем значение движущей силы, воспользовавшись формулой (3) (таблица 2): F = цтд • cosa + та + тд • sina, где т = 150кг; д = 10^; ц = 0,25 [3]; а = 1,3 СМ .

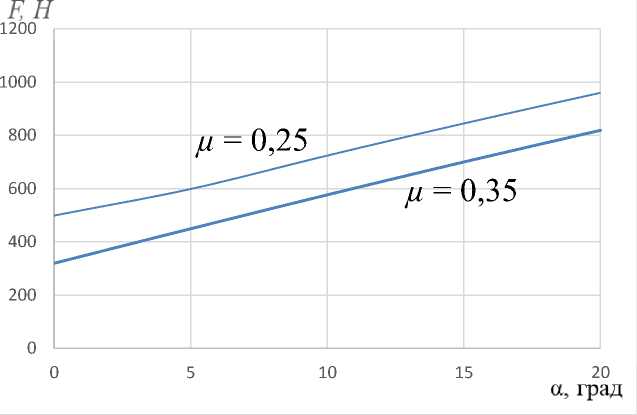
Рисунок 3 - Зависимость движущей силы от угла наклона при v_p Ф v_cp4

Произведем расчет при разных значениях коэффициента трения в равноускоренном движении роботизированной платформы. Воспользуемся ГОСТом 9128-2013, в котором принято следующее значение коэффициента трения, равное 0,25 - 0,35 [3].

Таблица 2 - Зависимость движущей силы от угла наклона при v_p Ф а_ср . _ч

α, град	0	5	10	15	20
F , Н	570	700	825	946	1060

По графику видно, что при меньшем значении коэффициента трения равное 0,25 движущая сила в два раза меньше, следовательно, для дальнейших расчетов примем F = 570 H; g = 0,25; a = 0° .

Воспользуемся ранее выведенной формулой, показывающей зависимость движущей силы от изменения угла склона:

I

F = ^.mg • cosa + ma + mg • sina а = 7             '

Подставим полученную формулу для нахождения ускорения роботизированной платформы в первое уравнение, связывающее силу и угол наклона. Покажем зависимость средней скорости от основных механических характеристик роботизированной платформы:

F = ^mg • cosa + m^^- + mg • sina, Перенесем все значения, не содержащие скорость, в правую часть:

F — ^mg • cosa + mg • sina = m^-,

Разделим обе части уравнения на у :

F(F-^.mg^cosa+mg^sina) ---------m ---------= ^V k ,

t • (—^g • cosa + g • sina + у) = VK,

Возьмем ранее полученные значения: F = 570 Н; a = 0°; m = 150 кг; g = 10 ^2; д = 0,25;

t = 1 с: произведем подсчет конечного значения скорости роботизированной платформы:

Vk = 1,29 7.

Следует подчеркнуть, что по ранее полученной формуле, показывающей зависимость скорости от основных механических характеристик роботизированной платформы при равноускоренном движении, скорость передвижения и его масса обратно пропорциональные величины, следовательно, при увеличении массы платформы скорость будет падать. Произведем анализ данной зависимости с целью получения допустимых значений грузоподъемности роботизированной платформы v к , м/с (таблица 3).

Таблица 3 - Зависимость скорости от массы

m , кг	80	120	150	180	210
м V k ,- с	4,6	2,25	1,3	0,7	0,2

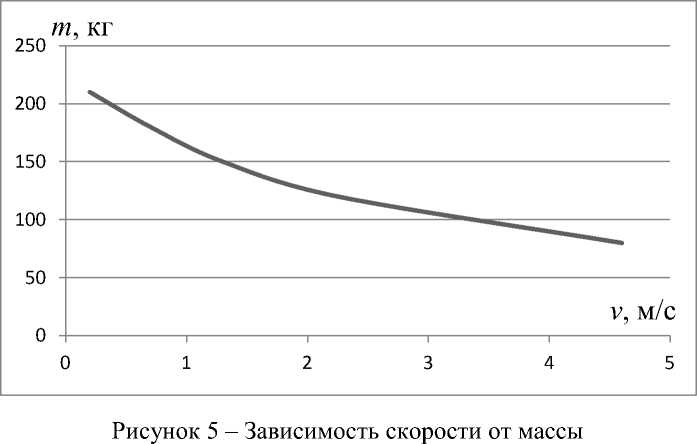
Исходя из расчетов и графика (рисунок 5), видно, что оптимальное значение скорости, близкое к допустимому значению 1,3 ^м , получается оптимальная масса роботизированной платформы является 150-210 кг, в случаях выше 210 кг на нее оказывается сильное сопротивление, из-за чего она не может разогнаться.

Заключение. Результаты исследования подтверждают, что движущая сила роботизированной платформы увеличивается с увеличением угла наклона поверхности и коэффициента трения. Также была установлена зависимость скорости от массы платформы: при увеличении массы скорость снижается. Эти данные необходимо учитывать при проектировании и эксплуатации платформ.