Анализ восстановления квадратурных составляющих по пилот-сигналам

Для систем радиосвязи важной проблемой является повышение помехоустойчивости приёма цифровых дискретных сигналов. В системах приема дискретных сообщений пилот-сигналы используются для восстановления квадратурных составляющих коэффициента передачи канала связи [1]. Применение пилот-сигналов позволяет дать оценку частотно-временного поля характеристик принимаемых сигналов и снизить вероятность ошибочного приема символов. Поэтому их число должно выбираться с учетом компромисса между снижением скорости передачи информации и качеством оценивания характеристик замираний. Для оценивания (интерполяции) частотно-временного случайного поля (СП) применяются различные методы, тесно связанные с моделями представления СП квадратурных составляющих [2]. Наиболее эффективно представление СП в виде двумерного марковского поля, что позволяет применять для восстановления калмановские алгоритмы [3]. Вместе с тем, это приводит к дополнительным ошибкам за счет замены реальных корреляционных функций (КФ), СП экспоненциальными. Таким образом, встает актуальная задача сравнительного анализа эффективности алгоритмов восстановления СП квадратурных составляющих в системах мобильной связи на основе известных и предложенных методов представления СП с помощью авторегрессий с кратными корнями характеристических уравнений.

Рассмотрим возможности восстановления квадратурных составляющих с корреляционной функцией (КФ) в пространстве частот. Для нахождения дисперсии ошибки оценивания квадратурных составляющих воспользуемся филь-

трацией Калмана при аппроксимации реальной дробно-рациональной КФ авторегрессионными (АР) процессами первого и второго порядка.

Оптимальная оценка вектора квадратурных составляющих записывается в виде [4]:

,

где P – ковариационная матрица ошибок оценивания. Используя формулы, запишем

, (2)

где V_x = M^xx ^г} – ковариационная матрица вектора значений квадратурных составляющих. Структура этой матрицы имеет следу-

ющий вид:

/ ^2

14 =

5*2 1

В_г 2

-2

ВВ

1 3

2 3

ВВ

1 м

2 М

, (3)

Rm 1

Rm 2

Rm г

где – ковариация между значениями квадратурных составляющих на частотах . Эту матрицу удобно переписать в виде:

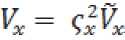
где

;

–

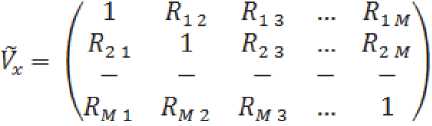
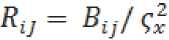
коэффициент корреля-

ции квадратурных составляющих, которые находятся по заданной КФ:

R.. = RQ< = i -j) = R(k) =

= R(M =

,

где                      – разность соседних

частот. уровне [5-6]:

Заданный интервал корреляции ^0 на 1/ e позволяет выбрать коэффициент £F

R(k0)=1 e

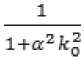
Ve—1 или a —     , где e – основание натурального

^0

логарифма.

Обычно применение фильтра Калмана основано на замене КФ экспонентой

^1(Ю = о^р^¹ ,       (7)

где Py находится из условия равенства W- . При этом p_Y = e ^o. e

Для повышения эффективности восстановления квадратурных составляющих будем использовать АР процесс с корнем характеристического уравнения кратности m=2 . При этом КФ

RiU^qi+^W^ , (8) где параметр p по заданному значению /Cq .

На рис. 1 приведены три графика КФ R®, R^k), R₂(k) при k_o = 10. Хоро шо видно, что КФ ^2 ( ^ D лучше аппроксимирует реальную частотную КФ 7? (k ).

ДИСПЕРСИЯ ОШИБКИ ДЛЯ ДВУХ ПИЛОТ-СИГНАЛОВ составляющих на 10 частотных позициях с дву- мя пилот-сигналами, расположенными на первой и девятой позициях.

При этом в формуле:

-1000000000

относительные дисперсии ошибок оценивания будут диагональными элементами матрицы.

^ = V_X(E+ q^CV^¹ ,   (9)

гдеq=^– отношение сигнал/шум. Структу- ра матрицы    имеет следующий вид:

/ »i    Лг/^Х  Лз/^Х  - Р1м/о,\

L₌  ^21/^    "2    ^2з/"х   - PimIOxX

,(0)

Vmi/Ox  Рмг/oi  Рмз/»х  -   Ом ’ где °1 ~ ^eXI^x^I ~ aE^iax,…,

^M — т2 – относительные дисперсии оши- бок оценивания квадратурных составляющих.

a^ = si^Truz^ =.

Представлены графики при, как для q=10, так и для q=100, (рис. 3, 4).

Из рисунков 3 и 4 видно, что АР моделей с кратными корнями характеристических уравнений и КФ R2(k) (АР процесс с корнем характеристического уравнения кратности m=2) немного проигрывает по дисперсии ошибки по отношению к фильтрации с КФ R(k). Предложенный подход R(k) более эффективен, чем остальные методы фильтрации.

Представленное на рис. 2 в качестве примера рассмотрим восстановление квадратурных

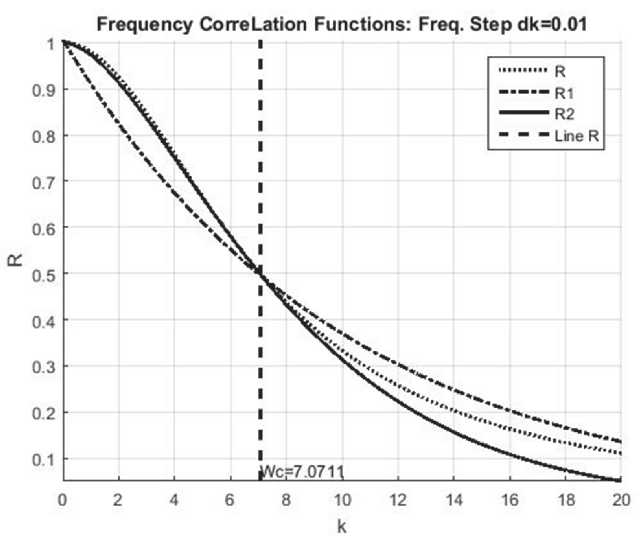
Рис. 1. Корреляционные функции по частоте dk = 0,01, где dk – дискретность шага.

1 23456789 10

Рис. 2. Расположение двух пилот-сигналов

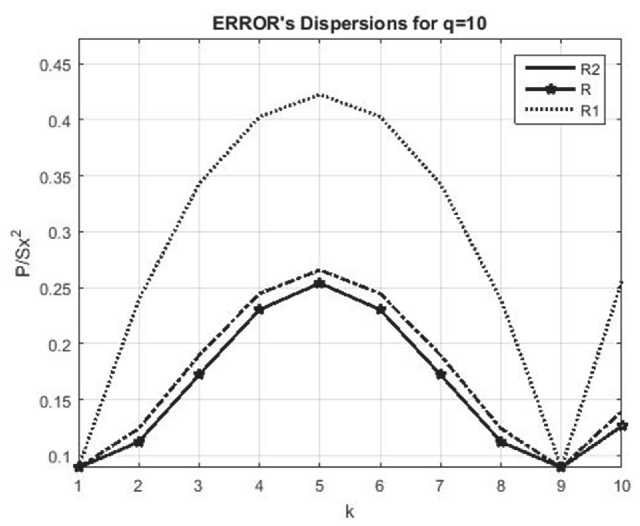
Рис. 3. Относительная дисперсия ошибки при

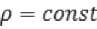
:, q = 10

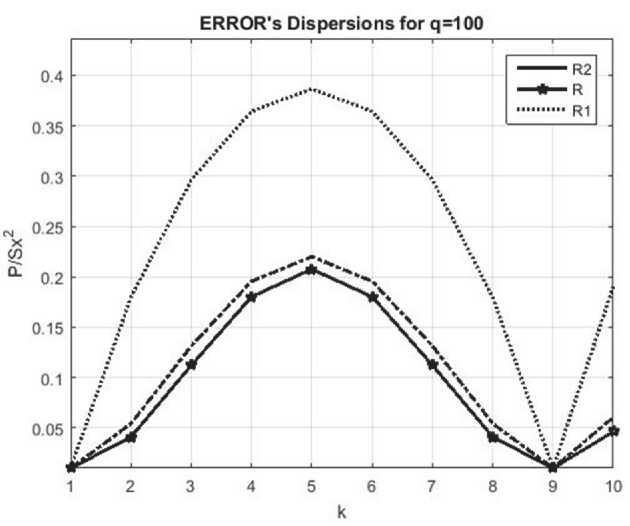
Рис. 4. Относительная дисперсия ошибки при р = \5 'ль t, q = 100

При анализе эффективности восстановления значений квадратурных составляющих по частоте произведено сравнение алгоритмов Калмана, авторегрессионных процессов с корнями характеристического уравнения. Установ лен существенный (в 2 - 3 раза) проигрыш по величине дисперсии ошибки восстановления при использовании классической калмановской фильтрации с экспоненциальной аппроксимацией R 1 (k). Вместе с тем, авторегрессионные мо- дели обеспечивают возможности применения восстановления квадратурных составляющих по пилот-сигналам в реальном масштабе времени.

ДИСПЕРСИЯ ОШИБКИДЛЯ ЧЕТЫРЁХ ПИЛОТ-СИГНАЛОВ

Представленное на рис. 5 рассмотрим восстановление квадратурных составляющих на 10 частотных позициях с четырьмя пилот-сигнала-ми, расположенными на первой-второй и восьмой-девятой позициях.

При этом в формуле:

С = 0000001000 0000000010

относительные дисперсии ошибок оценивания будут диагональными элементами матрицы.

^ = V_X(E+ q^CV^¹ ,   (6)

где q= — – отношение сигнал/шум. Структу- T²

ра матрицы имеет следующий вид:

a2

P^/^ P13fOx - Р1м/Ох\

»2    ^23/^   ™ РгМ^х I ,(7)

^мг/^х Рмз!^х — ^ам /

ZT² — ZT² /zr² ZT² — ZT² /zt²

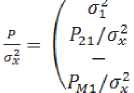
где ^1 ~ ^QexI^QX»°T ~ ^ETi^X ,   …,

^м —    – относительные дисперсии оши бок оценивания квадратурных составляющих.

a^ = si^Truz^ =   .

Представлены графики при p = const, как для q =10, так и для q =100, (рисунки 6, 7).

Как следует из анализа кривых на рис. 6 и рис. 7, применение АР моделей с кратными корнями характеристических уравнений и КФ R ₂(k)

практически не приводит к проигрышу по дисперсии ошибки по отношению к фильтрации с КФ R(k). Заметим, что использование классической калмановской фильтрации с экспоненциальной аппроксимацией R1(k) реальных КФ проигрывает предложенному подходу в 2-3 раза по дисперсии ошибки восстановления при не- значительном уменьшении вычислительных затрат. Вместе с тем, АР модели обеспечивают возможности применения калмановского восстановления квадратурных составляющих по пилот-сигналам в реальном масштабе времени.

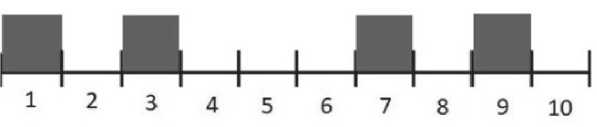
Рис. 5. Расположение четырёх пилот-сигналов

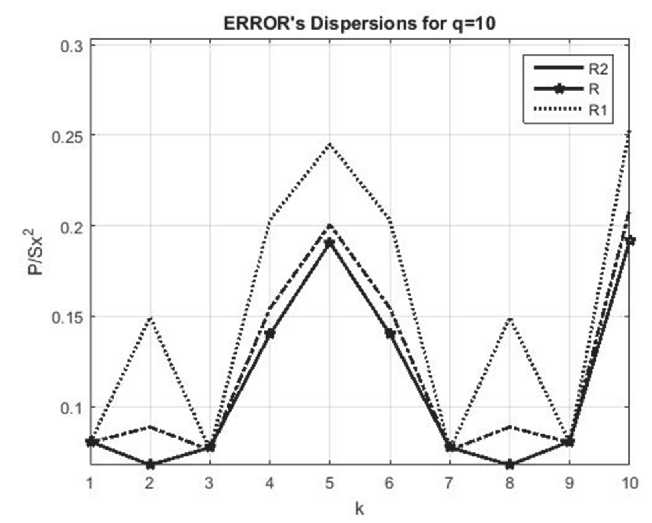
Рис. 6. Относительная дисперсия ошибки при

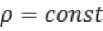
, q = 10

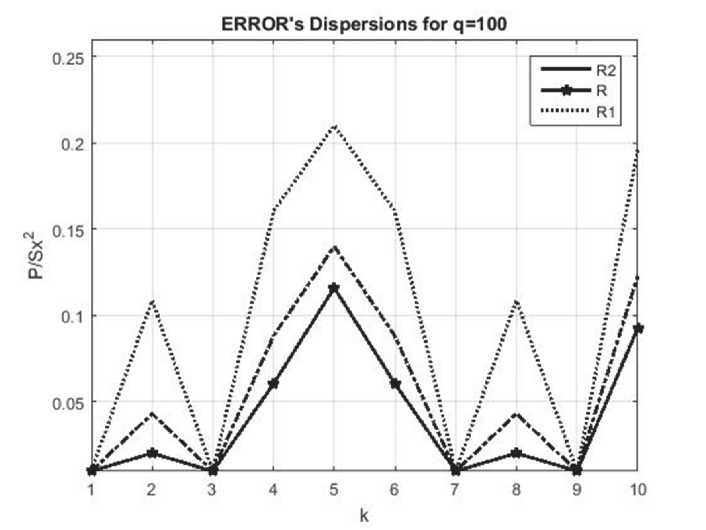
Рис. 7. Относительная дисперсия ошибки при р = const, q = 100

ЗАКЛЮЧЕНИЕ

В работе представлен анализ эффективности алгоритмов восстановления случайных полей квадратурных составляющих в системах мобильной связи на основе известных и предложенных методов представления случайных полей с помощью авторегрессий с кратными корнями характеристических уравнений. Предложено осуществлять восстановление полей канала связи в реальном масштабе времени на основе калмановской фильтрации с применением АР моделей с кратными корнями характеристических уравнений. Установлено, что использование классической калмановской фильтрации с экспоненциальной аппроксимацией R ₁ (k) реальных КФ проигрывает предложенному подходу в 2-3 раза по дисперсии ошибки восстановления при незначительном уменьшении вычислительных затрат.