Анализ задачи дифракции света на микрооптике гибридным методом конечных элементов - граничных элементов

—- = itopHy,(1)

дх

-z = -i®pHx ,(2)

дy

—- ——- = itoe(x, У) Ez дх ду

**

для ТЕ- поляризации: Е = (0,0, Е_z ), H = ( H_x , H y ,0);

дН —- = -itoe(x, у)Еу , дх (4) дИ —— = ie(x, у)Ex , ду (5) дЕy дЕ —- —у22 = -itopHz, (6) дх ду —— для ТМ-поляризации: Е = (Ex,Еу ,0), Id = (0,0, Hz); где ю - циклическая частота излучения, ц - магнитная проницаемость среды, Е, Н - вектора электрической и магнитной напряженности электромагнитной волны.

Из систем (1) - (3) и (4) - (6) следует уравнение Гельмгольца вида:

д	■ X д у ( х , у ) "	д	■ X д у ( х , у ) "	+
дх	L a дх J	ду	L a ду J	(7)

+ к о PV (-, У) = 0, где для ТЕ-поляризации p       е (х, у)

V = Е z , а = —, в = -^z., Р 0         ^е 0

, I------ to 2п ко = tope =— = — - волновое число в вакуу-

• • с А

• ме, Ц0, £0 - магнитная и электрическая постоянные; для ТМ-поляризации:

• 2. Метод Галеркина и метод конечных элементов

„      е ( х , у )       p

V = H z , а =----- , в = — .

е ₀         p ₀

Из теоремы Грина [2] для двух произвольных функций на плоскости (х, у) следует

JJ [ V p ( x , у )V q ( x , у ) ++ p ( x , у )V² q ( x , у ) ] dxdy = n

= J P (x, у)         ' di, s           дn д — д —                д2   д2 д2

где V = —ех + —е - градиент, V =—- +—- - дх ду у                    дх2 ду2

лапласиан, — - производная по направлению, за-дn даваемому внешней нормалью n к замкнутому контуру S области Q, dl - дифференциал вдоль линии контура S.

Для ТЕ- поляризации уравнение (8) запишется в виде

JJ — vvv q - koei(x, у) x nL Pi x y(x, у)q (x, у)]dxdy =                     (9)

= J q ^{( x} ’ у ) I V ^dl

В методе Галеркина [3] искомое поле ищется в виде разложения по базисной системе интерполирующих функций:

N

V ^{( х} , У ) = Е C n V n ^{( x} , у )•                    ⁽¹⁰⁾

n = 1

В качестве системы линейных интерполирующих функций можно выбрать функцию вида n = (k,l) - двойной индекс):

.   x_k - x у, - у                  _,₍₁₎

1---- , если x, у е Й (у

А А                     ^к’¹

1 - x^-x А ’ 1+у^-у, Vki(x, y)= А 1 + Ук-^У + А . xk - x 1 + к А , 1 - у^-у, А если x, у е ^к22 если x, у е ^к31)

А^- , если x, у е ^к ⁴ ) если x, у е ^к⁵⁴ если x, у е ^к⁶⁴

где А - шаг сетки отсчетов, показанной на рис. 1.

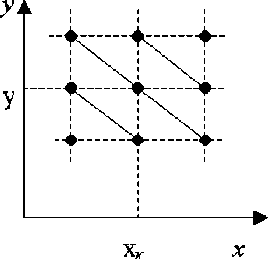
Рис. 1. Фрагмент триангуляции

На рис. 1 показаны также области линейной аппроксимации Q кР ) , p = 1,6 . Подставляя в уравне

ние (9) разложение (10) и выбирая в качестве функции q ( x , y ) базисную функцию v _kl ( x, У ), получим систему алгебраических уравнений для поиска коэффициентов разложения С т :

N N Г Г 1

ЕЕ C m C l Uf — ^V m ^V V l -

• I = 1 m = 1        (_QL ^P l

• - к S ( x , У) V m ( x , У) v i ( x , У ) ] dxdy -        (12)

  - f v i ( x , У ) д ^ ^" ( x , У ) dl ( = 0

s dn I

Система уравнений (12) - однородная и поэтому имеет единственное нулевое решение. Сделать ее неоднородной можно с помощью наложения граничных условий. Например, в задаче Дирихле считается известным световое поле на границе рассматриваемой области:

• v ( х , У ) = Р ( х , У ),( х , У ) е S ,                  ⁽¹³⁾

N

Е C m M ml = ^- ff g ⁽ x , У ) Vl ^{( x} , У ) ^dxdy .      ⁽¹⁷⁾

m = 1              П

а в задаче Неймана считается известной производная по нормали:

d V ( x , У )

'     = q ( x , У ), ( x , У ) е S                 (14)

д n

Пусть среди N узловых точек на плоскости, принадлежащей рассматриваемой области, М точек принадлежат границе S, тогда внутри области Q будет N-M точек. В задаче Дирихле М коэффициентов С т оказываются известными:

М

Р ^{( х} , У ) = Е ^C m V m ⁽ х ’ У )’ ⁽ х ’ У ) ^{е S         (15)}

т = 1

Тогда вместо однородной системы уравнения (12) получается неоднородная система уравнений:

N

Е C m A ml = bl                         (16)

m = M + 1

3. Вариационный подход в методе конечных элементов: метод Ритца

Если в операторном уравнении

т; u=f(18)

^^.

Линейный оператор L - положительный, то есть имеет место соотношение

(Lu, v)=(u, Lv)>0,(19)

то решение уравнения (18) эквивалентно минимизации функционала [4]:

E(u)=(Au, u) - 2(/; u),(20)

где (u, v) = ffu (x, y)v(x, y)dxdy - скалярное произве-n дение, f (u )= f|udl для неоднородной задачи Нейма-s dn на.

Для уравнения Гельмгольца будем иметь:

]L = - -1 A- к 2s_t ( x , y ),                     (21)

P l

E ( V ) = ff —- V A V - к02 s v ²( x , y ) dxdy L p i                         _

- 2 f fv«dl . S

-

Подставим в уравнение (22) разложение искомой функции ^ ( х , у ) по базису интерполирующих функций (10), получим:

N

E ( C m ) = Е C n C m B mn ,                   (23)

n

где

A ml = ff — ^V m ^V V l ^- n L p

к 0 S l ^{( x} , У >_т ^{( x} , y >! ^{( x} , y ^{) ]} d^xdy ,

M   ,      dv bl = Е Cm fvl(x, У) -;—(x, У)dl m=1 S          дП

где

B mn = ff — ^V V n V V m ^{- k}’° ^SVnV m ^dxdy ^{-nL P l}                         J .(24)

- 2f ^d_Vm^ l v d

_S д n ⁿ

Уравнение Эйлера получается приравниванием к нулю производной от функционала (23):

дЕ^С т¹ = 2^ Е C n B mn = 0.              (25)

^dC m      n = 1

M

- Е C m Л — ^V V m ^V V l — m = 1     Q _ ^P l

^k 0 ^S l

⁽ x , У ) V m ⁽ x , У ) V l ⁽ x , У

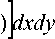
Определитель этой системы det( 1~_mn ) всегда отличен от нуля, т.к. является определителем Грама для линейно независимых интерполирующих функций v _m ( x , y ). Rang(E)

Неоднородной система уравнений (12) становится и в том случае, если внутри области Q имеются источники излучения, которые описываются функцией g ( x , у ) и которая появляется в правой части уравнения Гельмгольца (7). Тогда неоднородная система уравнения будет иметь вид:

4. Метод интегральных уравнений Фредгольма второго рода

Рассмотрим для ТЕ - поляризации двумерную задачу дифракции плоской волны на прозрачном теле. Для этого выберем область Q 1 и Q 2 как показано на рис. 2: Q 1 - это область прозрачного однородного тела, например цилиндрическая линза, Q ₂ - это

Сложив уравнения (30) и (31) с учетом граничных условий (27), получим

внешняя однородная область; обе области разделены контуром S.

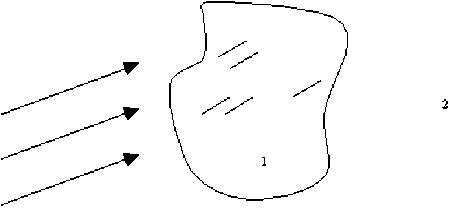
Рис.2. Дифракция плоской волны на прозрачном объекте

⁽ к 12 - к 2 ) J J V 1 G 2 dxdy - V 0 ( x , у ) =

Ц

V 1 ,( x , y ) eQ 1

^- У 2 ^{,( x} , У ) ^еЦ 2

Для полей ^ i и ^₂ из Q ₁ и Q ₂ требуется решить дифференциальное уравнение Гельмгольца [5]:

( А + к2) ^ 1 = 0,( x , у ) eQ i ,

^{( А +} k22) ^ 2 =- g 2 ^,( x , У ^{) еЦ} 2 ,

где g 2

источник во внешней области Q 2,

к 12 = -П^£'1,2Ц112 — волновое поле для сред 1 и 2, с граничными условиями, которые следуют из непрерывности на границе раздела двух сред тангенциальных составляющих напряженностей электрического и магнитного полей:

У\\ S = V 2I S ^,( x , У ) ^e S ,

d V i

дn S

^g V 2 дn

,

S

где v ₀( x , y ) = JJ g ₂ G ₂ dxdy - поле в области Q₁ или Ц

Q₂, созданное источниками с функцией - g ₂( x , у ). Далее мы предполагаем, что точечный источник находится далеко от области Q₁ и Т₀( х , у ) можно рассчитывать как плоскую волну.

Первое из уравнений (32) является интегральным уравнением Фредгольма второго рода относительно функции поля Т₁ ( х , у ), ( х , у ) e Q₁ решив его и найдя функцию Т₁( х , у ) с помощью второго из уравнений (32) можно найти внешнее рассеянное поле ^ 2 ( х , у ), ( х , у ) e Q 2 .

Если X = к 2 - к 2 не является характеристическим значением уравнения, т.е. не удовлетворяет соотношению

X J J V ₁ G ₂ dxdy = V ₁( x , у ),                   (33)

П 1

то решение уравнения (32) можно выразить через соответствие функции V п } и собственные числа X п ,

n - нормаль к контуру Q₁ внешняя область Q₂. Функция Грина для двумерных световых полей (цилиндрическая волна) равна функции Ханкеля второго рода нулевого порядка

G 1,2 ⁽ x , x ' , у , у ') =

= H 0 ²⁾ ( к 1,2 V ( x — x У + ( У — У У) ’

первый член асимптотического разложения, который имеет вид:

H j _|^2,( x ) = J —exp( - ix + i^П ), x ^^        (29)

V n x          4

Применение формулы Грина [2] к уравнениям (26) дает:

г ( дv₁ _       дG ₂ I „

। G 2 — 1 г dl + s l д n          д n

+ ( к ² - к ₂ ² ) J J V ₁ G ₂ dxdy =                  ⁽³⁰⁾

Ц

V 1 , ( x , У ) е^ 1 , 0, ⁽ x , у ) е^ц 2 ,

Г J ^д V 2_Г^дG 2 L, J l2 V 2 ттг ^d1 s l д п д ⁿ

J ^{0,( x} ’ У ) ^eQ1 g 2 G 2 dxdy = l            ~

Q ^j             l^- V 2^{,( x} , У ) ^еЦ2

удовлетворяющие уравнению

^X n J J ^V n ^G 2 ^dxdy = ^V n ^{( x} , У ),                 ⁽³⁴⁾

П 1

следующим образом [6]:

V 1 ^{( х} , у ) = V 0 ^{( х} , у ) ⁺

+ ( к 2 - къ± . ^S,V: ( x - y l .

1 = 1 X l - ( к 1 - к 2 ) где g i = J J V q( x , у) V 1 ( x , у ) dxdy . ц

В методе конечных элементов уравнения (32) сводятся к системе алгебраических уравнений. Используя разложение искомого поля по базису интерполирующих функций (10) вместо первого из уравнений (32), получаем линейную систему алгебраических уравнений:

N

^^ CmDmn = On on ,                      (36)

m = 1

где

D mn = ( к 1 ² - к 2 ²) X

^X J J V m ^{( x} ‘ , У ' ) G 2 ⁽ x n , У п ; ^x ‘ , У ' ) ^dx'dy' ^- .

Q 1

• ^- V m ^{( x} n , У п X V 0 n = V 0 ⁽ x n , У п )

• 5. Метод граничных интегральных уравнений

Интегрирование в (32) происходит по двумерной области Q1. Чтобы уменьшить объем вычисле- ний рассмотрим сведение задачи о дифракции плоской волны на прозрачном теле к системе интегральных уравнений, в которых интегрирование происходит по границе области (в двумерном случае - по контуру). Для этого заменив в уравнении (30) G2 на G1 (при этом k = k2, и второе слагаемое в уравнении (32) будет равно нулю) и используя граничные условия (27) получим систему из двух граничных интегральных уравнений [5]:

j l-^ r ¹ G 1 ^- V 1 'У' 1 ^dl = 0, ( x , y ) eQ 2 ,

S | dn           8 n J

двумерном теле можно найти в [7]. В этом методе точки ( х к , у к ) из уравнения (40) выбираются на контуре S. Тогда вместо системы (37) в случае отсутствия источников можно записать:

, l0Vr дG L, 1     /ас

Ji -т~ G1 - V1 — Jdl = -V1,    (x, y)e S,

Idn         dn J 2

S

0V _r    d G L,   1   / а с МП

^G 2 - V 1^ J ^dl = -7 V 1 , ⁽ x , y ) ^e S . ⁽⁴¹⁾ d n           d n J       2

■ dl = V o , ( x , y ) eQ 1 . (37)

Система уравнений (37) имеет единственное ненулевое решение. Необходимость ее заключается в том, что область определения правой части (37) -двумерная плоскость, а область определения левой -замкнутая линия S. После решения системы уравнений (37) поля в областях Q 1 и Q₂ находятся по формулам:

X 5V1 Г Ш 5G

J G1 -V1^

S L dn          8 n

dl = V 1 , ( x , y ) еП_ь

г a_V i          d G 2

V0 -J ~ G 2 - V1“2

S L dn          8 n

dl =

= V 2 ,   ^{( x} , y ) ^eQ 2.

Представляя поле V 1 и его нормальную производную по границе S в виде кусочно-линейной аппроксимации

M

V 1 ^{( x} , y )| S = L C m⁾ V m V m ⁽ x , y ) ,

Если уравнения кривой S задано в виде ломаной линии, то вместо правых частей в уравнении

Гт   6 Г        9

(41) появятся выражения: I 1-- V 1 и-- v 1 , со-

(  2п J      2п ответственно, где 0 - угол излома контура в выбранной точке (х, у) e S, то ее единственное решение будет нулевым. Чтобы избежать этой ситуации можно выделить из первого уравнения известную часть поля, описывающую падающую волну:

V1 (х, У) = v1 (x, y) + V1 (x, y), где v1 ,V1 - рассеянное и падающее световые поля, а во втором уравнении рассматривать только рассеянное поле

V 1 ^{( х} , У ) = v 1 ^{( x} , y ).

Можно поступить наоборот, это зависит от того в какой области реально находится источник света в Q 1 или в Q₂. В методе, основанном на уравнении (41) в отличие от метода, основанного на уравнении (37), задействованы только точки на границе S. Это создает некоторые трудности при цифровой реализации метода, так как для определения М от-

d V 1 ( x , y ) d n

S

m = 1

M

S

= L C m² V m ⁽ x , У ) ,

m = 1

S

где М - число граничных точек, у т ( х , У ) — интерполирующие функции из уравнения (11), вместо системы (37) получим линейную алгебраическую систему уравнений относительно неизвестных C m и c m 2:

L Cm2^Mm. - Cm1 Nm. )=°> m=1

L ( C m 2 ¹ «2 - Cm¹ N mk ) = v ,. , m = 1

где

M m 2    V^V'_; ⁽ x ’ ^y ) G 1,2 ( x , y ; x . , y . ) dl ,

S     ^{d n}                           ,

⁽ x k , y . ) ^eQ 2 ,

N m ¹^ = j v m ⁽ x , y )

S

a G 1,2 ⁽ x , y ; x k , y . )

d n

dl ,

⁽ x k , У к ) ^eQ 1 -

Разновидность метода граничных интегральных уравнений для дифракции света на прозрачном

V

счетов функции V1\ s и М отсчетов функции ^ ¹

S

требуется 2М точек на границе S.

6. Гибридный метод конечных элементов

В [8] предложен метод расчета дифракции света на прозрачном двухмерном теле, сводящийся к решению системы из двух интегральных уравнений, одно из которых получается по вариационному методу и методу Ритца по формула (24), (25) и одно из граничных уравнений (41). Система уравнений имеет вид:

Е (VS) = JJ{V(VS + V^VS + Vi) -Q

- к(2^si^VS + V )2 }dxdy - -J (vS + V)   (VS + V) dl

S           dn

N

VS (x, y ) =L CmVm (x, y ), m=1

d E ( v ^S ) ^d v m j J^ v i S I a n

= 0,

,

G 1 ^- V S ' У ' J = ¹ V^S , ⁽ x , y ) ^{e S} , 8 n I 2

где ψ ^S ( x , y ), ψ ⁱ ( x , y ) неизвестное рассеянное и известное падающее световые поля, например с ТЕ – поляризацией в двумерной области Ω, ограниченной контуром S.

Численный пример.

Рассмотрим дифракцию плоской ТЕ-поляризованной волны на диэлектрическом однородном цилиндре с круглым сечением. Пусть плоская волна падает на цилиндр слева направо вдоль оси x , длина волны λ 0 = 1 мкм. Относительная диэлектрическая проницаемость цилиндра ε = 2 , радиус равен 0,5 мкм. Окружающее цилиндр однородное пространство имеет параметры ε = µ = 1. Расчет производился гибридным методом конечных элементов по формулам (42). В качестве области Ω выбирался квадрат размером 2х2 мкм, а контура S – периметр области Ω . Число точек разбиения квадрата было равно N = 80x80. После нахождения проекции на ось z электрического вектора E_z внутри области Ω и на ее периметре S , рассчитывалось поле вне области Ω в области Ω 2 с помощью теоремы Грина по второй из формул (41). Внешняя область Ω 2 имеет размеры 8х6 мкм и число отсчетов – 320х240.

На рис. 3 показана двумерная картина дифракции (распределение интенсивности поля) на круговом цилиндре. Видно, что максимум интенсивности находится внутри диэлектрического цилиндра вблизи задней точки его поверхности. При определенных параметрах наличие максимума интенсивности внутри элемента микро-оптики может привести к его разрушению. Данный эффект надо учитывать при проектировании ДОЭ.

Рис. 3. Распределение амплитуды, полученное гибридным методом

На рис.4 показано распределение интенсивности в зависимости от полярного угла вокруг цилиндра на расстоянии равном 1 микрон от его центра, то есть интенсивность по периметру кругового цилиндра.

Заключение

В данной работе рассмотрен метод конечных элементов в различных вариантах, применительно к двумерной задаче дифракции световой волны на диэлектрическом теле с цилиндрической поверхностью и с произвольным сечением.

Одним из рассмотренных методов проведено численное моделирование дифракции плоской волны с TE-поляризацией на круглом цилиндре с диаметром, равном длине волны. Заметим, что результаты расчета методом конечных элементов дифракции на круглом цилиндре с высокой точностью совпали с результатами расчета по аналитическим формулам точного решения задачи.

A

0,6

О -------------------------------------------1------------------------------------------1--------------------------------------------1-----------------------------------------1--------------------

90           180           270           360 angle

Рис. 4. Распределение амплитуды по периметру цилиндра

Работа поддержана Российским фондом фундаментальных исследований N 98-01-00894, 99-0139012, 00-01-00031, 00-15-96114.