Анализ задачи кручения трансверсально-изотропного полого цилиндра малой толщины с переменными модулями сдвига

r 1 <  r <  r ₂, 0 <ф< 2 п , - L <  z <  L .

Уравнение равновесия в перемещениях при отсутствии массовых сил имеет вид [1]:

# G       - 11+ 5 G 1 E 1 ;■ - ^и Ф 1 + G _{] (}p)^= 0.

др ^     ( dp p )J p ^ dp p J         S^ ²

Здесь p = r/r0, £ = z/r0 — новые безразмерные переменные, r0 =(r1 + r2)/2 — радиус срединной поверхности цилиндра, pe[p1;p2] (ps = rs/r0, s = 1,2), £g[—l; l] (l = L/r0); иф= иф(p, £) — компонента вектора смещения; G = G(p), G1 = G1 (p) — безразмерные упругие характеристики (модули сдвига), рассматриваемые как произвольные положительные кусочнонепрерывные функции переменной p.

Предполагаем, что боковая часть цилиндра свободна от напряжений, т. е.

—

= ^{G (} p ⁾ (^d U 7

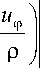
= 0, ( s = 1,2 ) ,

p=p s

CTPФ а на торцах цилиндра заданы следующие граничные условия:

^.    Gi (p)dur    = f ±(p), d^ 5=± i где f ± (p) — достаточно гладкие функции, удовлетворяющие условиям равновесия.

Решение (1) будем искать в виде:

и ф ( p , ^ ) = v ( p ) m ( ^ ) ,                                            (4)

где функция m(^) подчинена условию m "(^)-Ц2 m (£,) = 0.                                          (5)

После подстановки выражения (4) в уравнения (1) и (2) с учетом условия (5) получим:

(

G ( р ) и' ( р )

V г

—

и(р)

‘

G ( р ) ^и' ( р ) V

—

р р 7

р=р ,

= 0.

и' ( р ) — ^^У + ц ² G ( р ) и ( р ) = 0,

V         р 7

Рассмотрим несколько частных случаев зависимости упругих характеристик от р.

Квадратичная зависимость . Допустим у цилиндра модули сдвига заданы в виде функций

G ( р ) = g 0 р ²; G ( р ) = g 1 р ², где g ₀ , g ₁ — постоянные.

С учетом зависимостей (8) из уравнений (6) и (7) имеем:

г

и" ( р ) + - и' ( р ) + g ¹ Ц 2 р        V g 0

р

—

Л 1^и ( р ) ⁼ 0, р 7

^⁽р ² «’ ( ^р ) ^—р« ^{( р )} ) |_ , =°-

Уравнения (9) и (10) можно представить в следующем виде:

A и = ц ² и ,

где

A и = <

—

g ₀ ( d 2 и   3 d и 3  ³

+        ^и gi V d р   р d р р

;

2 d и р —— ри d р

р=р ,

= 0

.

A — самосопряженный оператор в гильбертовом пространстве L2 (р1;р2) с весом р3. Все собственные значения Xk (A) — вещественные, а соответствующие им собственные функции — ортонормированные:

р 2

( ^U k , ^U n ) = J ^U к ( р ) ^U n ( р ) р ^{3 d} р = ⁸ kn .                                  ⁽¹²⁾

р 1

Общее решение (9) имеет вид:

и ( р ) = р ^—1 ( AJ ₂ ( Рр ) + BY 2 ( Рр ) ) ,                               (13)

где р= I—ц;  J2 (рр), Y2 (рр) — функции Бесселя первого и второго рода g0

соответственно; A , B — произвольные постоянные.

С помощью уравнения (13), удовлетворяя граничным условиям (10), относительно A и B получаем однородную линейную систему алгебраических уравнений. Из условия существования нетривиальных решений этой системы имеем характеристическое уравнение:

^А ( Р , р 1 , р 2 ) =

Р ² р 1 р 2 +

V

Р ^р 1 ^р 2

—

^ ^ ^^^ру"

р 1 р 2     7

L 11 ( в )

+

+[ 4 вр 1

V

^—lix 7 ^{L o ( в ) +}

(         32 1      .

4 вр 2 — -- I L 01 ( в ) + 16 L 00 ( в ) = 0,

V        ^вр 2 7

где

L , -( P ) = Л(Рр 1 ) 7 -(Рр 2 ) — Л -(Рр 2 ) Y i ( Рр 1 ) , ( i , j = 0,1 ) .

Левая часть трансцендентного уравнения (14), как целая функция параметра ц, имеет счетное множество нулей с точкой сгущения на бесконечности.

Проанализируем характеристическое уравнение (14). Положим

P i = 1 -е ; р 2 = 1 + е ,                                           (15)

Г — Г где е = ——1 — малый параметр, характеризующий толщину цилиндра.

2 r 0

Подставляя выражения (15) в уравнение (14), получаем

^A i ( ц , P i , P 2 ) = D ( ц , е ) = 0.                                          (16)

Функция D ( ц , е ) при е >  0 имеет две группы нулей со следующими асимптотическими свойствами:

• а)    первая группа состоит из двукратного нуля ц = 0;

• б)    вторая группа состоит из счетного множества нулей, которые имеют порядок O ( е ¹ ) .

Приведем схему доказательства этих свойств. Представим D ( ц , е ) в следующем виде:

D ( ц , е ) = 4^ | i + f 16 - 2g ц ² )е ² +fц ⁴ - 2 g ¹ ц ² + 32\⁴ + ... | .         (17)

^п g 0 [ ( ^{3   3} g 0    J    ( 15 g 0 ²       g 0        ³ J

Отметим, что D (ц, е) = ц2 D0 (ц, е) и limD0 (ц,е) = C (0< C <да). ц^0

То есть ц = 0 является двукратным нулем D ( ц , е ) .

Покажем, что все нули D0 (ц, е) неограниченно возрастают при е > 0. Предполагаем обратное. Допустим цk ^цк ^да при е > 0. Тогда справедливо предельное соотношение D0 (цк, е) = еD* (цк) при е > 0. Предельные точки множества нулей цк при е > 0 определяются из уравнения D* (цк ) = 0. В рассматриваемом случае D* (цк ) = 2g1. Следовательно, V                                                         V 7 п g 0

предположение о существовании ограниченных при е >  0 нулей несправедливо.

Определим характер стремления цк к да при е > 0. При е > 0 возможны следующие случаи: 1) ецк ^ 0; 2) ецк ^ const; 3)ецк ^да. Аналогично методу [2] можно показать, что случаи 1 и 3 здесь невозможны.

Для построения асимптотики нулей второй группы отыскиваем их в виде:

ц к = ^ + O ( е ) .                                      (18)

е

После подстановки выражения (18) в характеристическое уравнение (14) и преобразования его с помощью асимптотических разложений функций J _v ( рр ) , Y _v ( рр ) ( v = 0,1 )

для 8 _к получим:

sin

(

²J g ^{1 8} >

V V ^g 0

^

J

= 0, 8 к

п к

2 g ₁ / g ₀ ^.

Из уравнений (19) видно, что в отличие от изотропной оболочки при фиксированных значениях k и при больших значениях g1 g0 (сильная анизотропия) показатель изменяемости напряженного состояния Sк стремится к нулю. В этом случае некоторые погранслойные решения не обладают свойством затухания и могут охватывать всю область, занятую оболочкой.

Приведем асимптотическое построение однородных решений, соответствующих группам нулей, которые рассмотрены выше.

Перемещение и напряжения, соответствующие корню ц ² = 0 , определяются следующими формулами:

u ф ¹⁾ ( р , ^ ) = 4 )р^ ^ф^ ⁰ , ^ ф5 = g 1 A 0 р ³.

Полагая р = 1 + еп ( - 1 ^п^ 1 ) и раскладывая по малому параметру е решения второй группы, находим для них следующие асимптотические выражения:

и ⁽²⁾- u ф =

с

\

■ S _к cos

g1 z S2sin рф             к е к=1

g ^{1 s} к ^{( 1 -}п ) + О ^{( е ) т}к ⁽^ ,

V ^g 0           J

( Г— к 1

к

к

g ^{1 s} к ( 1 ^-п ) ⁺ O ( ^е ) ^т к ( ^ ) , g 0           J _

, _ от

=$= g 1 Е

где m k ( ^ ) = F k e ^{ц к} Ч E k e

— I

к = 1

Ц к

.

g ^{1 S} к cos g ₀

\

к

Е s к ( 1 -л/L O ^{( е )} m№ ,

V g 0          J

Укажем характер построенных решений. Перемещение представим в виде:

от uф (р, 5) = A0р^ + Е ик (р) тк (^).

к = 1

Во второе слагаемое включены перемещения, определяемые вторыми группами решений.

На основе уравнения (22) для напряжений получим:

от

^ ф2 = g 1 A 0 р ^{3 +} g 1 Е р 2 ^и к ( р ) ^т к ( ^ ) , к = 1

^ рф = g 0 Е ( р 2 ^и к ( р ) ^- р^и к ( р ) ) ^т к ( ^ ) .

к = 1

Для крутящих моментов M _ёб напряжений, действующих в сечении ^ = const, имеем:

р ₂

M _ёб = 2 n J С ф^ р ² d р .

р ₁

Подставим уравнение (23) в выражение (25):

^п g 1 ( р 6 ^-р 6 )

M ёд =      3

от

Г р 2

к

A o + 2 ^п g i Е J р 4 ^и к ( р ) d р m' k ( ^ ) .

к = 1

к Р 1

Умножим обе части уравнения (9) на р ⁴ и проинтегрируем полученное выражение в пределах [ р 1 ; р ₂ ] :

— ц ² J р ⁴ и к ( р ) d р = з р 2 р ² и к ( р ) d р - J р ⁴ и к ( р ) d р -3* J р ³ и к ( р ) d р . g ⁰      р 1                           р 1                        р 1                           р 1

С помощью интегрирования по частям и с использованием граничного условия (10) из выражения (27) получим:

Р 2

J р ⁴ и к ( р ) d р = 0.

P i

Подставим зависимость (28) в уравнение (26):

ⁿ g 1 ( p 6 ^— p 6 )

M ^ё6 =      3

Формулы (20) определяют внутреннее напряженно-деформированное состояние цилиндра. Напряженное состояние, соответствующее второй группе решений, имеет характер пограничного слоя и первые члены его асимптотического разложения эквивалентны краевому эффекту Сен-Венана в теории трансверсально-изотропных плит [2].

Рассмотрим вопрос о снятии напряжений с торцов цилиндра. Как было показано, несамоуравновешенную часть напряжений можно снять при помощи проникающего решения (20), причем связь постоянной A ₀ с крутящим моментом определяется равенством (29).

Подставим уравнение (23) в граничные условия (3)

« g 1 Epuk (p)mk (6)

k = 1

= f 1 ± ( p ) .

6=± l

где f±(p)=f ±(p)—p3. n(p2 —p1 )

Умножая выражение (30) на pu _n ( p ) и интегрируя в пределах [ p ₁; p ₂ ] , с учетом уравнения

• (12) получаем:

mn (6)U 1=t±, т. е.

( h n e ^Ц n ⁶ F n ^—

H n e ^—

' ■ ⁶ E - )l =± l = t ± .

1 p 2

Здесь t ± = — J Z 1 ^± ( p ) ^U n ( p ) p d p .

^g 1 p i

После решения уравнения (31) определим неизвестные постоянные F_n и E_n :

F n =

t V n^l

n

—

t ^—е^—ц nl n

2 Ц n sh ( 2 Ц n l ) ’

E n

t+e^—H n l n

—

t ^—е^ц nl n

2 Ц n sh ( 2 Ц n l ) "

Линейная зависимость . Допустим модули сдвига заданы в виде:

G ( p ) = g o p ; G i = g i p ,

где g ₀ , g ₁ — постоянные.

С учетом зависимости (32) из уравнений (6) и (7) имеем: ^u4p ^{) +} j ^u ' ⁽ p ^{) +} [ g ¹ h ^{2 —}pr ] ^{u (} p ^{) = 0} , M^{p ) —u ( p ))}L =p. = 0.

s

Общее решение (33) имеет вид:

u ( p ) = p

— I

¹² ( C 1 J 3/2 ( Pp ) + C 2 Y 32 ( Pp ) ) ,

где C ₁, C ₂ — произвольные постоянные.

С помощью выражения (35), удовлетворяя граничным условиям (34), характеристическое уравнение:

получаем

^А 2 ( ц , Р 1 , Р 2 ) =

г

х sin ^ ц

g ₁

_^ +

V g 0 (Р 1 Р 2

9 Р 1 Р 2 ^{— 3} Р 2 ^— 3 Р 2 g 0

^р 1 ^р 2

g ₁

ц—1 +    7- ц g 1 р1 р2

— 3

х

—

³ ( р 2 ^—Р 1 )    ⁹ g 0 ( Р 2 ^— Р 1 ) — 2

_2_2           _ _3_3    ц р1 р2          д1р1 р2

х

7 —     >

х cos

Трансцендентное уравнение (36) имеет счетное множество корней ц k .

Подставляем выражение (15) в характеристическое уравнение (36):

А 2 ( ц , Р 1 , Р 2 ) = Q ( ц , е ) = 0.                                     (37)

Уравнение (37) имеет две группы корней: а) первая группа состоит из двукратного корня ц = 0, который не зависит от е; б) вторая — из счетного множества корней ц k = — + O (£), £ которые при е > 0 стремятся к бесконечности.

Перемещение и напряжения, соответствующие корню ц ² = 0, имеют вид:

u ^(р , ^ ) = B 0 р^ ^ Р^ 0, ^ .: = g i B 0 Р ².                      ⁽³⁸⁾

Формулы (38) определяют внутреннее напряженно-деформированное состояние цилиндра.

Постоянная B ₀ пропорциональна крутящему моменту M _êð напряжений, действующих в сечении

^ = const таким образом:

^{2 п} g 1 ( р 2 ^— Р 5 ) м ёб =---------- B 0 .

Перемещение и напряжения, соответствующие второй группе корней, по своей структуре имеют вид (21) и соответствующее напряженное состояние имеет характер пограничного слоя.

Выводы. Решения (20) и (38), соответствующие корню ц ² = 0, определяют внутреннее напряженно-деформированное состояние цилиндра. Напряженное состояние, соответствующее второй группе корней, с порядком O ( е ^—1 ) имеет характер пограничного слоя. В этом случае некоторые погранслойные решения не обладают свойством затухания и могут охватить всю область, занятую цилиндром.