Аналог теоремы Лаврентьева - Зорича о глобальном гомеоморфизме для отображений с неограниченной характеристикой

Основные утверждения настоящей статьи анонсированы в работе [5] без приведения какой-либо аргументации. Доказательство основного результата в данном тексте приведено схематично, поскольку здесь мы в значительной мере опираемся на замечание из работы [2, с. 532, 2-й абзац].

В 1938 г. М.А. Лаврентьевым было сделано предположение о том, что локально квазиконформные отображения пространства R ³ являются гомеоморфизмами. Хорошо известным математиком В.А. Зоричем было получено следующее решение проблемы М.А. Лаврентьева (см. [1]).

Если f : R n ^ R n , n >  3, локально гомеоморфное квазирегулярное отображение R n , то f является гомеоморфизмом, причем на все пространство R n .

Основная цель настоящей заметки заключается в распространении гипотезы М.А. Лаврентьева о глобальном гомеоморфизме, доказанной В.А. Зоричем в его работе [1], на более широкий случай. Мы покажем, что отображения f : R n ^ R n , n >  3, удовлетворяющие относительно общим геометрическим соотношениям в окрестности бесконечно удаленной точки, являющиеся локальными гомеоморфизмами пространства R n , n >  3, инъективны. Необходимо заметить, что В.А. Зоричем был получен и более общий вариант его теоремы (см., напр.: [2]). Упомянем также недавнюю работу

М. Кристи [12] по этому поводу.

Перейдем теперь к определению упомянутых выше классов отображений. Как известно, в основу геометрического определения квазиконформных отображений, заданных в области D из R n , n >  2, положено условие

M ( f (Г)) <  KM (Г)                            (1)

для произвольного семейства Г кривых y в области D, где M — конформный модуль семейства кривых (внешняя мера, определенная на семействах кривых в R n ), а K >  1 — некоторая постоянная. Другими словами, модуль любого семейства кривых искажается не более, чем в K раз. Пусть теперь в основе определения отображения f лежит неравенство вида

M ( f (Г)) <  j Q(x) • p n (x)dm(x),                          (2)

D где m — мера Лебега в Rn, ρ — произвольная неотрицательная борелевская функция, такая что произвольная кривая y семейства Г имеет длину, не меньшую 1 в метрике р, то есть криволинейный интеграл первого рода J p(x)|dx| по каждой кривой y € Г удовле-γ творяет условию: J p(x)|dx| > 1, а Q : D ^ [1, то] — некоторая (заданная) веществен-γ нозначная функция (см., напр.: [16]). Изучению отображений, удовлетворяющих соотношению (2), посвящено значительное количество работ (см., напр.: [3; 5–8; 11; 12; 16; 17]). Отметим, что В.М. Миклюков исследовал некоторые классы отображений, удовлетворяющих аналогичным оценкам в терминах емкостей на поверхностях (см., напр.: [4]). При этом неравенство вида (2) анонсировано без приведения доказательства в работе [8] для так называемых отображений, квазиконформных в среднем. В частном случае, когда в соотношении (2) имеет место условие Q(x) < K п.в., мы снова приходим к неравенству (1). В общем случае, когда это не обязательно так, неравенство (2) означает, что искажение модуля исходного семейства Г происходит с некоторым весом Q(x), M (f (Г)) < MQ(x)(Г) (см. работы А. Казаку Каберия [10] и М. Кристи [12]).

Как уже было отмечено выше, локальные гомеоморфизмы f, удовлетворяющие соотношениям вида (1), называемые в этом случае локально квазиконформными отображениями , инъективны при n >  3 (см., напр.: в [1]). Достаточно простой пример отображения f (z) = e ^z указывает, вообще говоря, на неверность последнего утверждения при n = 2.

В настоящей работе обозначены некоторые аналитические условия на функцию Q из более общего, нежели (1), соотношения (2), отличные от банального требования ее ограниченности, при которых локальные гомеоморфизмы f, удовлетворяющие неравенству (2) для произвольного семейства кривых Г и любой р € admГ, инъективны в R n при n >  3. Вопрос о точности условий в работе не обсуждается, однако, как показывает схематично построенный нами пример (см. теорему 2), ни одно из этих условий нельзя заменить на требование Q € L p , p >  1. Некоторые приложения нашего основного результата (теорема 1), относящиеся к гомеоморфизмам классов Соболева W lOcn , могут быть найдены в заключительной части статьи (следствие 1).

1. Определения и предварительные сведения

Всюду далее D — область в R n , n >  2. Запись f : D ^ R n предполагает, что отображение f непрерывно. В дальнейшем R n = R n U{to} — одноточечная компактификация R ⁿ ,

B(x ₀ , r) = { x E R n : | x — x ₀ | < r } ,     B n = { x E R n : | x | < 1 } ,

S(x0,r) = {x E Rn : |x — x0| = r}, Sn-1 := S(0,1) , m — мера Лебега в Rn. Пусть Q : D ^ [0, то] — измеримая по Лебегу функция, тогда qx0(r) — среднее интегральное значение Q(x) над сферой |x — x0| = r, qxo(r) :=—Ц^г   [ Q(x) dS,                     (3)

ω n-1 r

|x-x0|=r где dS — элемент площади поверхности S, ωn-1 означает площадь сферы Sn-1 в Rn, Qn — объем единичного шара Bn в Rn, dist(A, B) — евклидово расстояние между множествами A, B C Rn. Борелева функция р : Rn ^ [0, то] называется допустимой для семейства Г кривых y в Rn , если jp(x) |dx| > 1

γ для всех кривых y E Г. В этом случае мы пишем: р E admГ. Модулем семейства кривых

Г называется величина

М (Г) =

inf

ρ ∈ adm Γ

j p ⁿ (x) dm (x).

D

Свойства модуля в некоторой мере аналогичны свойствам меры Лебега m в R ⁿ . Именно модуль пустого семейства кривых равен нулю, М (0) = 0, модуль обладает свойством монотонности относительно семейств кривых Г 1 и Г 2 : Г 1 C Г 2 ^ М (Г 1 ) <  М (Г ₂ ), а также свойством полуаддитивности (см. теорему 6.2 в [18]):

M

∞∞ иГi < £М(Г,).

i=1         i=1

Говорят, что семейство кривых Г 1 минорируется семейством Г 2 , пишем Г 1 > Г ₂ , если для каждой кривой y E Г 1 существует подкривая, которая принадлежит семейству Г ₂ . В этом случае М (Г 1 ) <  М (Г ₂ ) (см. теорему 6.4 в [18]).

Пусть E, F С R n — произвольные множества. Обозначим через Г(E,F, D) семейство всех кривых y : [a, b] ^ R n , которые соединяют E и F в D, то есть Y(a) E E,y (b) E F и y (t) E D при t E (a,b). Следующее понятие мотивировано одним из важнейших определений квазиконформности по Ф. Герингу, определившему квазиконформное отображение как гомеоморфизм f, искажающий емкость кольца в конечное число раз K, 1 <  K <  то (см. об этом раздел 13 в [13]). Пусть r ₀ = dist (x ₀ , dD), Q : D ^ [0, то ] — измеримая по Лебегу функция,

A(r i , r 2 ,x o ) = { x E R n : r i <  | x — x o | < r 2 } ,

S i = S ( x ₀ ,r i ) . Говорят, что f : D ^ R n является кольцевым Q-отображением в точке x ₀ G D, если соотношение

M ( f (r(S i , S 2 , A))) <  I Q(x) • n n ( | x - X 0 | ) dm(x)

A

выполнено для любого кольца A = A ( r 1 ,r 2 ,x ₀ ), 0 < r 1 < r ₂ < r ₀ и для каждой измеримой функции n : (r 1 , r ₂ ) ^ [0, то ] такой, что

r 2

j n ( r ) dr >  1.

r 1

Не лишним будет заметить, что условие (8) заменяет более общее требование допустимости (4) для специального семейства кривых Г (S 1 , S 2 , A). Заметим также, что если f является K -квазиконформным, то f удовлетворяет соотношению (7) при Q ( x ) = K G [1, то ). Исходя из сказанного выше, для нас в первую очередь представляет интерес случай неограниченных Q, ибо ситуация ограниченности последних полностью исследована в работе [1]. Пусть x ₀ G D. По аналогии, будем говорить, что

f : D \ { x ₀ } ^ R n является кольцевым Q-отображением в точке x ₀ G D, если соотношение (7) выполнено для каждой неотрицательной измеримой функции η, удо-

влетворяющей соотношению (8). При этом, здесь предполагается, что само отображение

f будет определено лишь в проколотой окрестности точки x 0 .

Для отображения f : D ^ R n , имеющего в D частные производные почти всюду,

пусть f ' ( x ) — якобиева матрица отображения f в точке x, ||f ' (x) | =

Внешняя дилатация отображения f в точке x определяется как величина

max heR n \{0}

If ‘ (x)h| |h|

K O ^{( x,f} )

ГМГ |J ( x,f )I ’

1 ,

J ^{( x,f} ) = 0 f ^' ( x ) = 0 ,

то , в других случаях

2. Вспомогательные результаты

Предложение 1. Предположим, что область D содержит начало координат, f : D \ { 0 } ^ R n , n >  2, — кольцевое Q-отображение в нуле. Пусть, кроме того, найдутся е ₀ > 0, е ₀ < dist(0,dD), и борелевская функция ^(t) : (0, то ) ^ (0, то ), удовлетворяющая условию

0 <

ε 2

I ( Е 1 ,Е 2 ) := У ^ ( t ) dt <  то

ε 1

для произвольных Е 1 ,Е 2 G (0,в ₀ ), такие что при е ^ 0

У Q(x) • ^ n ( | x | ) dm(x) = o ( I ^п ( е,е₀ )) . e<|x|o

Обозначим через Г семейство всех открытых кривых y (t) : (0,1) ^ R n , таких что Y(t k ) ^ 0 при некоторой последовательности t k ^ 0 и y (t) ^ 0. Тогда M ( f (Г)) = 0.

Доказательство. Заметим, что

∞

Г >U r i , i=1

где r i — семейство кривых a i ( t ) : (0,1) ^ R n таких, что a i (1) G S (0,r i ), где r i — некоторая последовательность, удовлетворяющая условиям r i < в ₀ , r i ^ 0 при i ^ то , и a i ( t k ) ^ 0 для той же последовательности t k ^ 0. Зафиксируем i >  1, и в G (0,r i ). Ввиду соотношения (9) имеем I ( в, r i ) > 0 при всех в G (0, r i ), где величина I ( в, r i ) также определяется из (9). Заметим, что функция

n(t) = { t I<^в-’- ₀ -

t ^G (^ r i ) , t G R \ (в, r i )

удовлетворяет условию нормировки вида (8) в кольце А ( в, r i , 0) = { x G R n : в <  | x | <  r i } и, следовательно, в силу соотношения (7)

M ( f (r(S (0, в), S (0,r i ),А(в,^, 0)))) <  I Q(x) • n n ( | x | ) dm(x) <  F i (в),

A(6,r i ,0)

где F _i (в) = I (_g^   J   Q(x) ^ ⁿ ( | x | ) dm(x). Учитывая (10), имеем F _i (в) ^ 0 . Заме-

ε<|x|<ε 0

тим, что при любом в G (0, r i )

r i >  г (S(0,в), S(0,r i ), А(в,r i , 0)) .

Таким образом, при каждом фиксированном i = 1, 2,..., из (12) и (13) получаем, что

M ( f (r i )) <  F i (в) ^ 0

при в ^ 0 и каждом фиксированном i G N. Однако левая часть неравенства (14) не зависит от в и поэтому M ( f (r i )) = 0. Наконец, из (11) и свойства полуаддитивности модуля, см. (5), следует, что M ( f (r)) = 0. □

Как и в работе [3], введем следующее определение, обобщающее понятие функций ограниченного среднего колебания по Джону — Ниренбергу (см. [14]). Будем говорить, что функция у : D ^ R имеет конечное среднее колебание в точке x0 G D, и писать у G FMO в x0, если lim

6 —>0

1 fi n • в ^п

/

В ( х о ,б )

| у(х) — у ₆ | dm(x) <  то ,

где у 6 = и— f у^{(х) dm(x)}. B(x 0 , 6)

Предложение 2. Пусть Q : D ^ [0, то ] — измеримая по Лебегу функция, D С R n , n >  2, x ₀ G D, такие, что выполнено хотя бы одно из следующих условий:

• 1)    Q G FMO ( x 0 );

n—1

2*) Q(x) <  C • (log РУ   ;

• 2)    q x o ( r ) = O ([ log r ] n 1) при r ^ 0;

• 3)    при некотором d ( x ₀ ) >  0, d ( x ₀ ) <  dist (x ₀ ,dD) и произвольных e E (0,5(x ₀ ))

  и

  
  

  δ(x 0 )

  /

  ε

  
  

  dt

  
  

  tq n - 1 ^(t)

  
  

  < ∞

  
  
  
  

  δ(x 0 )

  /

  
  

  dt

  
  

  = ОС .

  
  
  
  

  tq x n o - 1 (t)

  
  

Тогда можно указать e₀ e (0,1) и функцию ^(t) > 0 такие, что в точке х ₀ выполнены условия (10) и (9) предложения 1.

Разумеется, 2*) является просто частным случаем 2). Отметим, что если f является K -квазирегулярным отображением, то есть Q ( x ) = K в (7) для некоторой постоянной K >  0, каждое из условий 1)-3) предложения 2 автоматически выполнено. Отметим также, что соотношение (16) выражает собой интегральное условие расходимости, которое использовалось и ранее большим числом авторов (см., напр.: [15], [9] и [2]).

Доказательство. Не ограничивая общности, можно считать, что х ₀ = 0. Заключение предложения 2 в случае Q ∈ FMO следует из следствия 6.3 гл. VI [16], которое утверждает, что условие Q E FMO (0) при некотором е₀ > 0 влечет соотношение

Q(x) • ^ n ( | x | ) dm(x)

ε<|x|<ε 0

= O (loglogj) ,

где 0 < ^(t) := t _lo1_g i . Заметим также, что в обозначениях предложения 1 I ( e,e₀ ) :=

^{ε 0}                       log ¹

:= J ^(t)dt = log ^s 1 . Таким образом, соотношение (18) с учетом последнего завершает ε                     log _ε0

рассмотрение случая 1). Пусть теперь qx0(r) = O ([log Г]n 1) при r ^ 0. Фиксируем e0 < min { dist (0, dD), 1} . Полагаем ^(t) = t ljg i. Заметим, что

ε < |x| < ε 0

Q(x)dm(x)

n

(^{|x |} log я)

ε 0

-JU

ε      |x| = r

Q(x)dm(x)

n

(^{|x |} log я)

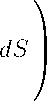
dr <  C • Ш п — 1 • I ( e,E o ) ,

ε 0

где, как прежде, I(e,e0) := J ^(t) dt и C > 0 — некоторая постоянная. Таким образом, ε случай 2) рассмотрен. Осталось рассмотреть случай 3). При каждом фиксированном ε0

e₀ < 5(x ₀ ) и произвольном e <  e ₀ рассмотрим функцию I ( e,e₀ ) = J ^ ( t ) dt, где

ε

/ i/[tq o ^{n - 1} (t)] , t E ( e,e o ) , [                 ⁰ , t ^{E ( e}, ^E 0 ) ,

где q ₀ (r) = q _x 0 (r), x ₀ := 0. Заметим, что I ( е,е₀ ) <  то при всех Е Е (0,Е 0 ) в силу предположения (16). Тогда ввиду (17) можно считать, что I ( е,е₀ ) > 0, е Е (0 ,е₀ ) . В таком случае функция ^(t), определенная соотношением (19), удовлетворяет соотношению (9) предложения 1. Кроме того, ψ удовлетворяет также соотношению (10), поскольку несложный подсчет показывает, что J   Q(x) • ^ n ( | x | ) dm(x) = ш _{п - 1} • I ( е,е₀ ) , при-

ε<|x|<ε 0

чем I ( е,е₀ ) = o ( I ^п ( е,е ₀)) ввиду (17). Предложение 2 полностью доказано. □

• 3.    Основной результат

Будем говорить, что отображение f : R n ^ R n есть кольцевое Q-отображение в точке х ₀ = то , если отображение f = f ^q-XF | 2^) является кольцевым Q -отображением в точке х ₀ = 0 при Q = Q (qxp) • При этом, используя замену переменных у := := Я2 в интеграле в правой части неравенства (7), можно переформулировать данное определение следующим образом. Отображение f : R n ^ R n будем называть кольцевым Q-отображением в точке х ₀ = то , если соотношение

M ( f (Г (S(0, R 1 ), S (0, R 2 ), A(R 1 , R 2 , 0)))) <  j     Q ( y ) • n n ( | y | )dm(y)       (20)

A(R 1 ,R 2 ,0)

выполнено для произвольных 0 < R 1 < R 2 <  то и произвольной неотрицательной измеримой функции п : (R 1 ,R 2 ) ^ [0, то ] такой, что

R 2

j n ( r ) dr >  1,

R 1

где множество A(R1,R2, 0) = A(R1,R2, x0) при x0 = 0 задается соотношением (6). Будем говорить, что функция у : Rn ^ R имеет конечное среднее колебание в точке то, если функция ^*(x) = у (я|2) имеет конечное среднее колебание в точке 0. Заметим, что отображение ^(x) = ^x2 подобно отображает сферу S(0, г) на сферу S (0,1/r), откуда следует, что |J(x,^)| = (1/|x|)2n. Согласно сказанному, прибегая к замене переменной в интеграле в правой части соотношения (15), мы снова можем переформулировать определение конечного среднего колебания в точке ∞ в следующем виде. Будем говорить, что функция у : D ^ R имеет конечное среднее колебание в точке то, пишем у Е FMO(то), если при R ^ то где ϕR

S I^x - ^Rl ^ |x|>R

оШ-

R n • / Hx)

|x|>R лировать условия вида 2), 2*)

ω n-1 · R ^n-1

и

^d _| ^m _x| ⁽ ₂ ^x _n ⁾ . Аналогично для бесконечности можно переформу-3) предложения 2 предыдущего раздела, соответственно:

■ j Q(x) dS

S(0, R)

Q(x)   = O Qlog | x | ] n 1)    при x >  to ;                    (24)

∞

/

dt

tq n - 1 (t)

= to

для некоторого do > 0.

Один полезный результат, используемый нами ниже, заключает в себе следующее.

Предложение 3. Произвольное гомеоморфное отображение f : D \ { 0 } ^ R n , удовлетворяющее условию вида (7) в точке х ₀ = 0 G D, имеет конечный или бесконечный предел в этой точке, как только функция Q(x) удовлетворяет требованию (10) предложения 1 при некоторой функции ^(t) с условием (9), см. лемму 4.1 и следствие 5.2 в [3]. При этом продолженное по непрерывности отображение f : D ^ R n является гомеоморфизмом в D.

Основной результат настоящей статьи заключает в себе следующая теорема.

Теорема 1. Предположим, что локальный гомеоморфизм f : R n ^ R n , n >  3, является кольцевым Q -отображением на бесконечности, то есть отображение f удовлетворяет условию вида (20) для произвольных 0 < R 1 < R 2 <  то и любой неотрицательной измеримой по Лебегу функции η, для которой выполнено соотношение вида (21). Предположим, что функция Q ( x ) удовлетворяет, по крайней мере, одному из условий:

• 1)    функция Q ( x ) имеет конечное среднее колебание на бесконечности, см. (22);

• 2)    выполнено хотя бы одно из соотношений вида (23)–(24);

• 3)    выполнено требование (25) при дополнительном условии Q ( x ) >  1 почти всюду.

Тогда f является гомеоморфизмом в R n , причем f (R n ) = R n .

Доказательство. Ограничимся здесь схемой доказательства, опуская подробности. Известным математиком В.А. Зоричем, установившим справедливость данного утверждения для случая ограниченных Q, было замечено (см. 2-й абзац на с. 532 в [2]), что доказательство гомеоморфности отображения f использует лишь тот факт, что модуль семейства кривых Г, уходящих на бесконечность, при рассматриваемом отображении f переходит в семейство Г ‘, такое что M (Г ‘) = 0. Воспользуемся теперь этим замечанием.

Из предложений 1 и 2 следует, что отображение f = f ^]ХХ|₂^ переводит семейство

Г 0 , состоящее из всех кривых, лежащих в R ⁿ и стремящихся по некоторой последовательности к точке х ₀ = 0 в семейство кривых, модуль которого равен нулю. Обозначая Дх ) = "]ХХ[ 2 и через Г ^ семейство всех неограниченных кривых в R n , мы имеем, что Г ^ = ^ (Г о ), и, значит,

M ( f (Г _ )) = M ((f о Д Г о ) = M (ДГ о)) = 0 .

Таким образом, гомеоморфность отображения f следует из сделанного выше замечания, на основе рассуждений из работы [1].

Поскольку f — гомеоморфизм в Rn, можно применить предложение 3 относительно инверсии f = f (|Х:0 в нуле, f : Rn\{0} ^ Rn. Тогда f — гомеоморфизм в Rn , при этом

множество f R ⁿ одновременно открыто и замкнуто в R ⁿ (как гомеоморфный образ компактного и открытого множества в R n ), то есть f (Rn) = R n и, значит, f (R n ) =

= R n . □

• 4.    О методе построения локального гомеоморфизма, для которого нарушена теорема типа Лаврентьева — Зорича

Прежде всего хотелось бы отметить, что для локальных гомеоморфизмов, удовлетворяющих соотношению (1), условия вида (22)–(25) автоматически выполняются, поскольку указанный случай соответствует неравенству (7) при Q(x) = K.

Следующий пример показывает, что условия на функцию Q(x), сформулированные в предыдущем разделе, являются точными в некотором смысле. Именно условия на

Q to)

∈ L ^p ни для какого (сколь

Q(x) нельзя заменить более простым условием угодно большого) р >  1.

Теорема 2. Для каждого р >  1 найдется локальный гомеоморфизм f : R n ^ R n , n >  3, удовлетворяющий соотношению вида (20) с некоторым Q(x), таким что Q ‘ (x) = Q (pxp) € L p (B n ), при этом f не является инъективным отображением в _R n _.

Доказательство. Зададим гомеоморфизм g : R n \ { 0 } ^ R n следующим образом:

1 + |х|а g(x) = —л— x, |x| где а € (0, n/p) (см. предложение 6.3 гл. VI в [16]). Это отображение является гомеоморфизмом, отображающим Rn \ {0} на множество {y € Rn : |y | > 1} в Rn, при этом, можно показать, что g удовлетворяет соотношению вида (7) в нуле с

^Q g ^(x)

1 + | x | ^a α | x | ^α

n-1

(см. [там же]). Заметим, что при | x | < 1 для некоторой постоянной C >  0 выполнено Q g (x) <  | _x | _a ( n - i) и, следовательно, Q g (x) € L ^p (B n ), поскольку ар <  n. Полагаем

h(x)

^g to) 2 g (№)Г

Заметим, что h — гомеоморфизм пространства R ⁿ на единичный шар B ⁿ , удовлетворяющий соотношению вида (20) с некоторой функцией Q _h (x) , причем по построению соответствующая функция Q h ^| Xx 2^ = Q g (x) суммируема в степени р в B n . Ясно, что единичный шар можно отобразить на некоторую область посредством локального q -квазиконформного отображения s(x), которое преднамеренно можно выбрать не инъективным. Полагаем f (x) = s ^ h(x). Построенное таким образом отображение, очевидно, не является инъективным в R ⁿ , однако удовлетворяет соотношению вида (20) на бесконечности с некоторой функцией Q f (x), в то время как соответствующая функция Q f (|Х 2) = q • Q g (x) суммируема со степенью р в B n . □

Напомним, что y ₀ € D — точка ветвления отображения f : D ^ R n , если ни в одной окрестности U точки y 0 сужение отображения f | U не является гомеоморфизмом. Совокупность всех точек ветвления f принято обозначать B f .

Предложение 4. Пусть x ₀ Е D, f : D \{ x ₀ } ^ R n — открытое дискретное отображение класса W 1 C ( D \ { x ₀ } ), для которого K O ^-1 (x, f) Е L^ ( D \ { x ₀ } ) и m ( B f ) = 0. Тогда f удовлетворяет соотношению (7) в точке x 0 при каждой неотрицательной измеримой функции η, удовлетворяющей (8), и вполне конкретном значении Q := K O ^-1 (x, f) (см. теорему 1 в [6]).

На основании предложения 4 и теоремы 1 получаем следствие.

Следствие 1. Пусть f : R n ^ R n , n >  3, — локальный гомеоморфизм класса W lO^ R n ), для которого K O ( x, f ) Е Ц; — 1 (R ⁿ ). Предположим, что функция Q = K O ^-1 (x, f) имеет конечное среднее колебание на бесконечности, см. (22), либо удовлетворяет хотя бы одному из соотношений (23)–(25). Тогда f является гомеоморфизмом в R ⁿ , причем f (R n ) = R n .

Замечание. Элементарный пример отображения f (z) = e z , действующего из C в C и являющегося локально квазиконформным Q ( z ) = 1, показывает, что при n = 2 теорема 1 и следствие 1 не имеют места.