Analogue Wavelet Transform Based the Predicted Imaginary Part of the Dynamics of Rational Map Having Zeros

Wavelet theory is based on analyzing signals to their components by using a set of basis functions. One important characteristic of the wavelet basis functions is that they relate to each other by simply scaling and translation. The original wavelet function, known as mother wavelet, which is generally designed based on some desired characteristics associated to that function, is used to generate all basis functions [1]. It is well known that the mother Morlet in Fig.1, is a modulated function composed of two quadrature components, characterized by the following equation:

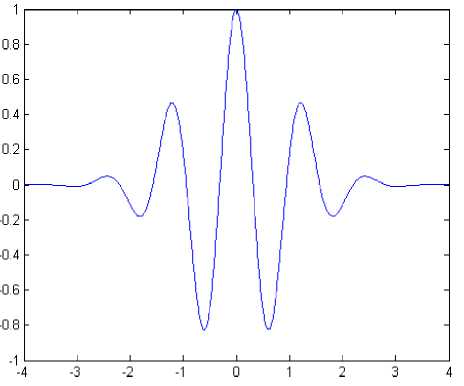
Fig.1. Morlet Wavelet

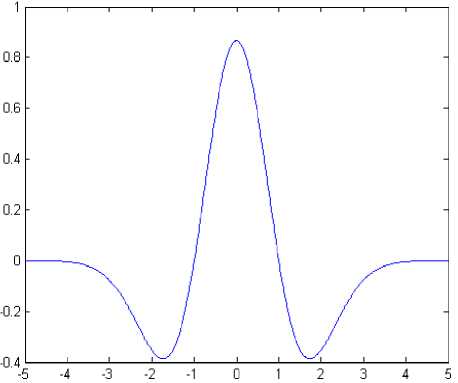
Fig.2 Mexican Hat Wavelet

wavelets and IFSs, is that large scale data may be compressed into a few functions or parameters. In the case of IFSs, only a few matrix entries are needed, and a finite set of vectors in R^d must be prescribed. As is shown in [8], this can be turned into effective codes for large images. Similarly (see [11]) discrete wavelet algorithms can be applied to digital images and to data mining. The efficiency in these applications lies in the same fact: The wavelets may be represented and determined by a small set of parameters; a choice of scaling matrix and of masking coefficients, i.e., the coefficients a in the scaling identity Eqn. (1.3) below

• [12] . The scaling function ф satisfies an important equation, called the scaling equation . This is obtained by considering the function ф ( A ¹ ) which lies in V ] C V .

Since the translates of ф form a basis for У_й then the scaling function is obtained:

The wavelet has been shown to be a very efficient tool for local analysis of non stationary and fast transient signals due to its good estimation of time and frequency localizations. This feature can be used to distinguish cardiac signal points from severe noise and interferences [4]. Wavelets find applications and have significant impact in various scientific areas including geophysics, hydrodynamics, econometrics, data processing, image compression, detection of discontinuities, neural networks, etc [5]. One of the reasons wavelets have found so many uses and applications is that they are especially attractive from the computational point of view. Computational efficiency of wavelets lies in the fact that wavelet coefficients in wavelet expansions for functions in V (resolution subspace in L ² ( R^d ) may be computed using matrix iteration, rather than by a direct computation of inner products: the latter would involve integration over R^d , and hence be computationally inefficient, if feasible at all. The deeper reason for why we can compute wavelet coefficients using matrix iteration is an important connection to the subband filtering method from signal/image processing involving digital filters, down-sampling and up-sampling. In this setting filters may be realized as functions m on a d-torus, e.g., quadrature mirror filters [6]. It would be interesting to adapt and modify the Haar wavelet, and the other wavelet algorithms to the Julia sets [7]

One of the applications of Iterated Functional Systems (IFSs), and their spectral theory, is to image processing [8] and [9]. IFSs include dynamical systems defined from a finite set of affine and contractive mappings in R^d , or from the branches of inverses of complex polynomials, or of rational mappings in the complex plane. A unifying approach to wavelets, dynamical systems, iterated function systems, self-similarity and fractals may be based on the systematic use of operator analysis and representation theory [10]. In terms of signal processing, what the two have in common,

where

k e Z^d

⁽ ak ^ e Z

is a sequence of complex numbers.

Definition 1.1: Let z I— > R ( z ) be a given polynomial. Let P be a finite set of distinct polynomials each of degree less than the degree of R. Let K ² ( R , P ) be a space of functions F in H ² ( J ( R )) . We say that F is in K ² ( R , P ) iff there are functions F_p ( z ) in H ^{2 ( J ( R} )) indexed by P such that

F (z )=2 p(z ^P (R (z)) e P

(1.4)

It is easy to see that each K ² ( R , P ) is a closed subspace in H ² ( J ( R )) , so in particular it is a Hilbert space. The finite family P that enters Eqn. (1.4) is a family of generalized filters. It depends on the particular polynomial z — R ( z ) , and we can expect to find solutions to Eqn.(1.4) in Definition 1.1 from the kind of representations of the Cuntz algebras the authors studied in their work on wavelets on fractals [9].

In this paper we will deal with the complex iteration systems which generate Julia sets in the Riemann sphere. If

Dynamics of Rational Map Having Zeros

n ,           n —1 ,     ,        0

P ( z ) _ pnz  + ^pn — 1 z    + ... + ^p о z

^Z O(zA       m         m —1 +  +    0   ^.

Q ^{( z} ) qm^z + qm _— 1 z    + ... + q 0 z

is a rational function with P , Q polynomials z G C , and N = max(deg P ,deg Q ) then R : X ( R ) ^ X ( R ) is N — to — 1 except at the singular points of R. The Julia set X = X ( R ) is the complement of the largest open subset of C where Rⁿ is a normal family.

Let R : C ^ C be an analytic self-map of the complex plane to itself. We will assume that it is either the Riemann sphere or the complex plane. In our investigation we have only concentrated on complex plane. For the notations and the relevant definitions cf. [13]. We will be considering as a discrete dynamical system [14] on the phase space, so we are interested in the behavior of the iterations of the said function by itself, that is, the n-fold compositions of with itself. Much work has been done for complex quadratics [14].

A. Beardon [15] has investigated the iterations of rational functions and its properties.

But we have tried to study the complex valued rational function which arose out of the solution of Classical Yang- Mills equation by Witten [16]. SelfDual and Anti Self Dual solutions of classical Yang-

Mills Equations correspond to solutions electromagnetic field tensor

of the

F v =d ц A v ~d v А ц

(1.8)

where we identify

F^{l 0} = E¹ ; F i =

-£ijkBk

*

vv      vv

Explicitly, the contravariant and covariant of the electromagnetic field tensor are:

(1.9)

metrical gauge field A [16]. The solutions are given by, ц k a — z

G ( z ) ⁼П 4--- (1.13)

i=0 a^ + z where a is the zero of the function g(z) and it is arbitrarily chosen complex number with the only restriction that Re a^ > 0. — a * is the pole of the same function. Witten in [15] has imposed the restriction ona . Here we attempt to relax the said condition and consider any a G C, where C is the complex plane. In this present work we have made an attempt to study the dynamics of the following class of rational functions in Eqn. (1.9). Here k is the topological index cf. [16]. Throughout our study we have used C++ program [17] to construct the images. We have tried to investigate the images for the functions G(z) for k = 1 i .e.

aj — z

G ( z ) = 4---- (1.14)

^ai ^{+ z}

Computation of some Julia sets of rational maps having the same number of poles and zeros was discussed [18]. In [19] we have statistically analyzed the image obtained out of complex valued rational functions having single Pole. In this paper we have used Tiberius (Predictive Modeling Software) [20] as well as Matlab signal processing tool for generating wavelet based predicted imaginary part of sample II.

The present paper has the following sections: section 2 provides neural network model based on RMS type of error, section 3 presents the analysis of the ANN model using Matlab SPTool, section 4 , discuss the analysis of the model with autoSIGNAL,and we will wind with the conclusion.

F Vv

E ¹ E ^T t E ³

E ¹ 0

B ³

B ²

E ² B ³

B ¹

ЗА E ³

B ²

B ¹

0 J

(1.10)

^F v

E ¹

E ²

t E 3

E ¹ 0

B ³

B ²

E ² B ³

B ¹

ЗА E ³

B ²

B ¹

0 J

(1.11)

where

a     a

a a dv Av

abc b c

b AVAv

(1.12)

here a , b , c are SU(2) (i.e. Special Unitary

Group)

indices. Witten in [16] has chosen a cylindrically sym-

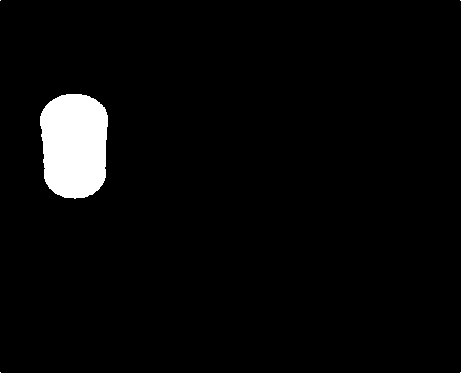
Fig.3. Computer Generated Image for c= (1, 0.1) int maxIterations = 10; double thresh = 10.0

Dynamics of Rational Map Having Zeros

Fig.4. Computer Generated Image for c= (1,0.1) int maxIterations = 100; double thresh = 10.0

• II.    Artificial Neural Networks Model

Artificial Neural networks are mathematical entities that are modeled after existing biological neurons found in thebrain. All the mathematical models are based on the basic block known as artificial neuron. A neural network is formed by layers of neurons. Fig.5. and Fig.6 show a simple neuron and One-Layer Network Architecture. A layer includes the inputs p, the weights matrix W , the summers, the bias vector b, the transfer function f and the network output vector a.

A layer whose output is the network output is named the output layer. All the other layers are called hidden layers.

Among the biologically inspired computing models are artificial neural networks (ANN). ANN does not approach the complexity of the brain, but both of them have two key similarities: the building blocks are simple computational devices and the connections between neurons determine the function of the network [21]. In Fig.7, we have developed the model using predictive modeling software known as Tiberius [20]. The neural network model has two inputs, thirteen hidden neurons and one output linear neuron. The two input variables are w and w , that is, the real parts of sample I and sample II respectively. The actual imaginary part of sample II and its predicted model are shown in Fig.8.

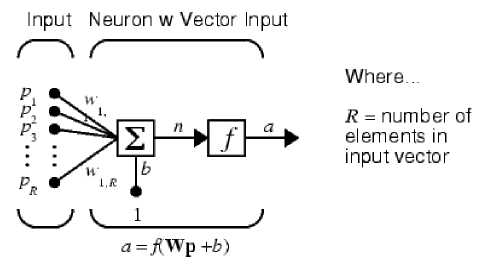
Fig.5. Simple Neuron

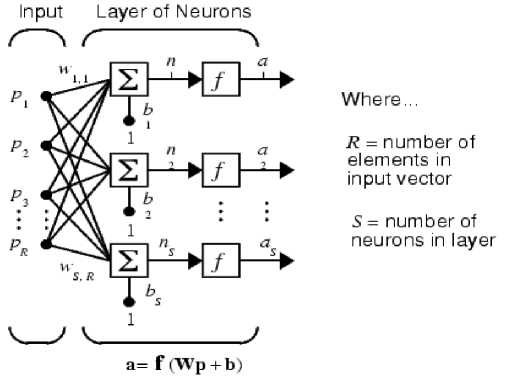
Fig.6. One-Layer Network Architecture

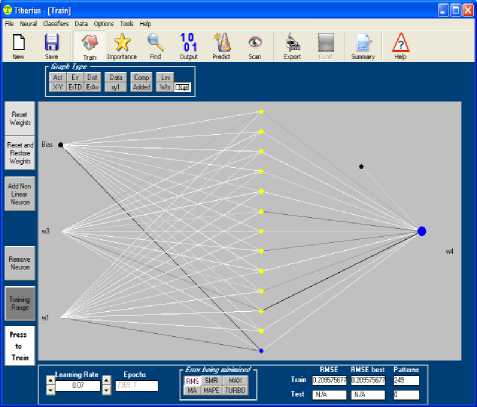
Fig.7. Artificial Neural Network Configuration

	w 1,1	w 1,2     .	.    w 1, R
	w 2,1	w 2,2    .	.    w 2, R
W =	.	.. ..	.               . .               .
	. _ w S ,1	.. wS ,1     .	.               . .    w S , R J

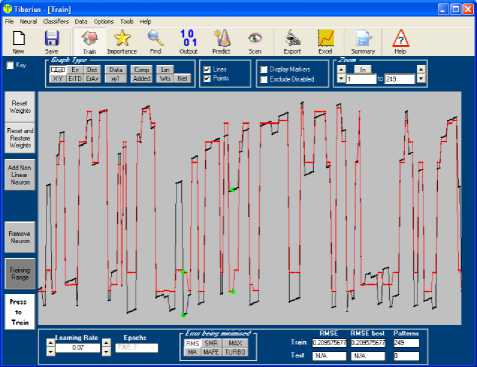
Fig.8. Actual and Modelled Values of w ⁴

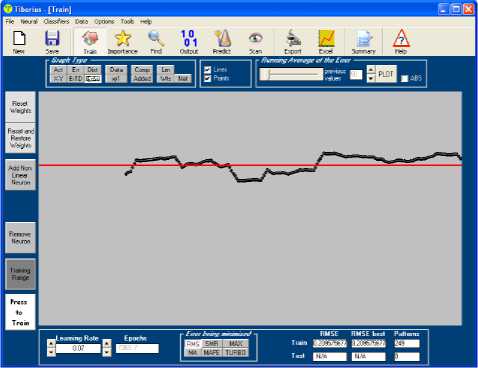
Fig.9. Smoothed Errors (for Time Series)

section. These are used to visualize waveforms and spectra of several signals and make a qualified filter design. Therefore, characteristic properties and desired parameters of signals have been estimated. In order to use a signal under these processes the signal was imported as a vector. The modeled imaginary part is plotted in Fig.10.

In our experiment we have considered two samples each of 249 data points from data points of the picture shown in Fig.3. w and w are the real parts of sample I and sample II respectively whereas w and w are the imaginary parts of sample I and sample II respectively. We now propose to model the imaginary part w of sample II in terms of real parts w and w as shown on the neural network in Fig.7. The predicted imaginary part w of sample II has 249 patterns and the Tiberius software has shown that the real part w of sample II is more important than the real part w of sample I in predicting the imaginary part w of sample II. The predicted imaginary part w of sample II was then imported as a vector of 249 patterns to Matlab workspace.

Let us consider the column data vector M of predicted imaginary part w of sample II,

M =

m ₁

m

• III.    Model Analysis Using Matlab

  Researchers in Applied Mathematics, Communications and Signal/Image Processing areas have developed many different wavelet systems and some are still actively working in designing even newer wavelets with specialized characteristics [1] but in many fields scientists are faced with the problem of recovering a true signal from incomplete, indirect or noisy data. Wavelets can help in solving the problem through a technique called wavelet shrinkage and thresholding methods that David Donoho has worked on for many years [22]. The technique consists of decomposing a data set utilizing wavelets by applying filters that act as averaging filters and others that produce details [23]. Some of the resulting wavelet coefficients correspond to details in the data set. In this section we are interested in the effect of band pass filter on artificial neural network model whose configuration is shown in Fig 7. We have first imported the model from Tiberius software to Matlab workspace then from Matlab workspace to signal processing tool with the sampling frequency of 8192Hz. This tool has three main components: signal section view, filter section view and edit as well as spectra

m

Let X ( t ) = [ x_T ( t ) x ₂ ( t ) . . . x ₂₄₉( t ) ] be the sampling vector signal with the sample frequency mentioned above.

Let w ( t ) be the sampled predicted imaginary part w of sample II with the same sampling frequency. Let us perform the vector multiplication on column vector M and row vector X ( t ), then we get:

w ₄ ( t ) = [ m_x  m₂

m 249 ]^X

Therefore,

Dynamics of Rational Map Having Zeros w4 (t) = m^i (t) + m^x^ (t) +... + m249x249 (t) (3.2)

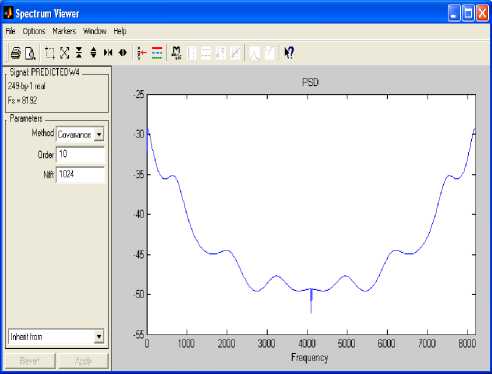
A stable band pass filter has been designed to analyze in this frequency range the predicted imaginary part of sample II. Fig.12 indicates the pole–zero plot of the filter. Magnitude, phase response, step response, group phase delay and other properties of the same filter are shown in Fig.13. The filtering process has eliminated noise successfully as indicated by power spectral densities (PSDs) of pre-filtering and post-filtering. The power spectral density of the predicted imaginary part of sample I is shown in Fig. 11 with minimum frequency equal to half of the sampling frequency. The PSD of the filtered predicted imaginary part of sample I is shown in Fig.15.

Let f ( t ) be the impulse response of the band pass filter,

Let y ( t ) be the response of the band pass filter, then

From Eqn. (3.2) we get

У ⁽ t ) = ^{f (} t ) * ^w 4 ⁽ t ) = ^m1 ^{f (} t ) * ^x 1 ⁽ t ) ^{+ m} 2 ^{f (} t ) * ^x 2 ⁽ t ) + ... + m ₂₄₉ f ( t ) * x 249 ( t )                           (3.3)

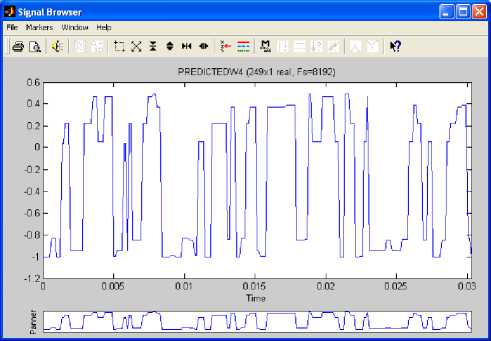
Fig.10. Predicted Imaginary Part ⁴ of Sample II

The filtered predicted imaginary part of sample II y ( t ) is shown in Fig. 14. The filtered signal is obviously a modulated signal. Hence we have successfully generated analog continuous wavelet transform from the model of imaginary part of sample II. The Matlab signal processing tool shows that the modulated signal generated out of the imaginary part of sample II is a real signal. Its expression can be easily derived from the equation of mother Morlet equation given in Eqn. (1.1) by equating the imaginary part to zero. Hence we get

w

Fig.11. PSD of the Imaginary Part ⁴

У(t) = w. ,t (t ) =

V .   )

(3.4)

Therefore

I t - T |

У ⁽ t ) = ^{f (} t ) * w 4 ⁽ t ) = cos ^Ю 0 I       I h_s , T ⁽ t )

V .  )

|У ⁽ t ) =| ^{f (} t ) * ^w 4 ⁽ t )|

(t- T \

= cos ^Ю о II h_s T ⁽ t )

V .  )

= h . , ( t )

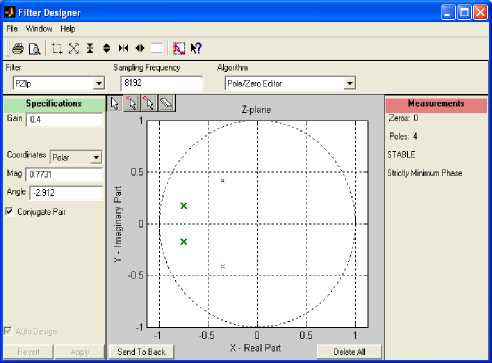
Fig.12. Filter Pole-Zero Plot

We therefore realize that the filter effect has generated a real wavelet transform whose magnitude is equal to the magnitude of the windowed function.

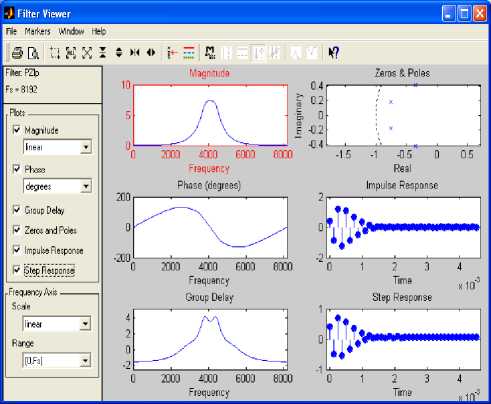
Fig.13. Filter Viewer

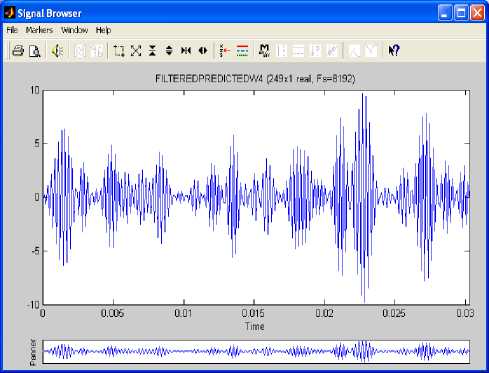
Fig.14. Filtered Predicted Imaginary Part

w ₄

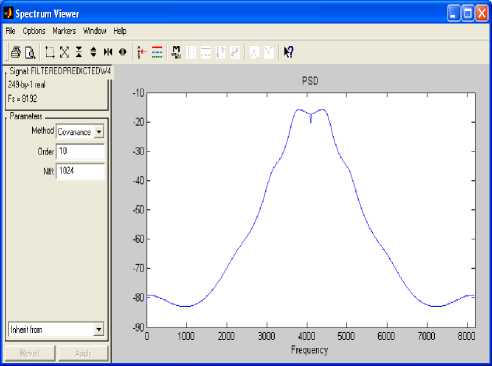
Fig.15. PSD of the Filtered Predicted Im. Part w ⁴

• IV.    Model Analysis UsinAutoSIGNAL

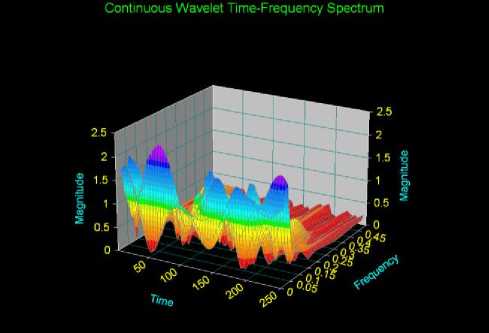
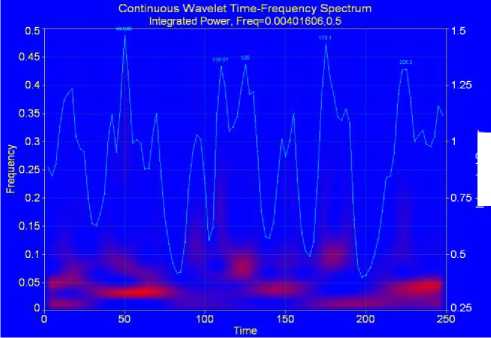
Finally we have imported the predicted values of the imaginary part w of sample II to autoSIGNAL, this is a cutting edge signal analysis software. We have been able to produce the Paul, Gaussian and Morlet mother wavelets using that computer tool. The mother wavelets mentioned above are ordered according to their time localization properties. The Paul wavelet has the best time localization capability amongst the three different mother wavelets, but at the same time it has the worst frequency localization. This makes the Paul mother wavelet more suitable for demodulating fringe patterns that exhibit high signal to noise ratio and rapid phase variations. On the other hand, the Morlet wavelet has better localization in the frequency domain than the Paul wavelet and it is more suitable for demodulating fringe patterns with slow phase variations and low signal to noise ratios [24]. In our work, we have selectively explored the properties of the generated wavelet transform based on Paul wavelet using autoSIGNAL, but the same analysis can be carried out on Morlet and Gaussian Derivative wavelets. The results obtained in this section confirm the results obtained in the previous section where we concluded that the modulated signal in Fig.14 is a wavelet. In addition to what the Matlab signal processing tool provides, autoSIGNAL provides the frequency and time range analyses of the integrated power contain in Paul wavelet as per Fig.19 and Fig.20. Paul wavelet Smoothing and Denoising as well as Filtering and Reconstruction are shown in Fig.21and Fig.22 respectively.

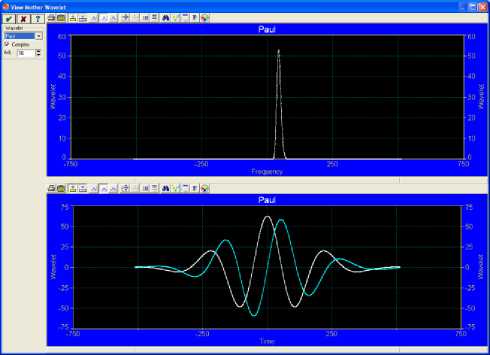
Fig.16. Wavelet of the Predicted Imag. Part

w ₄

w

Fig.17. Magnitude of the CWT of the Predicted ⁴

Integrated Power

Fig.20. Integrated Power for Frequency Range Analysis

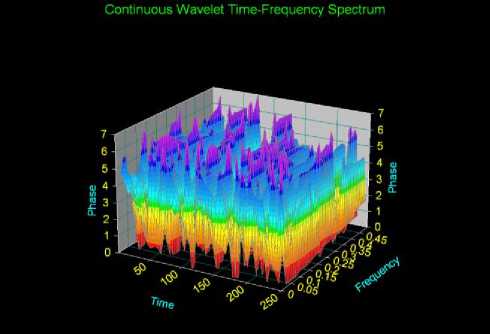
Fig.18. Phase of the CWT of the Predicted Im. Part

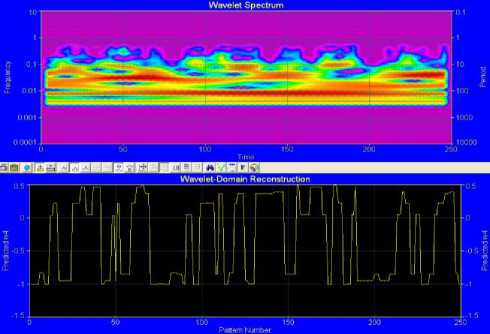
Fig.21. Wavelet Smoothing and Denoising

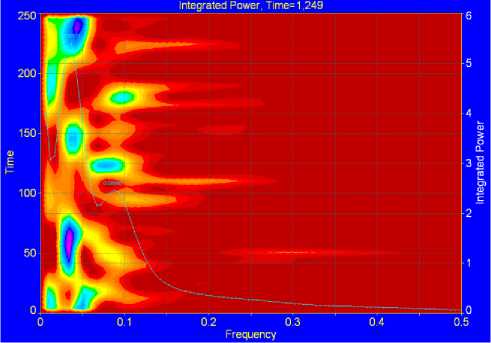
Fig.19. Integrated Power for Time Range Analysis

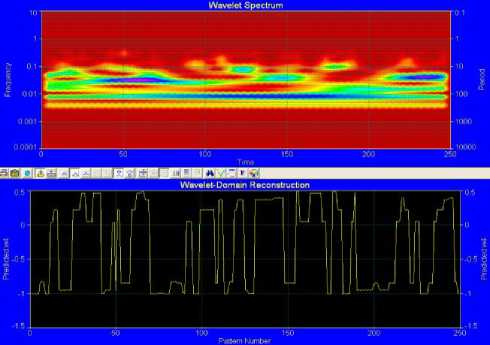
Fig.22. Wavelet Filtering and Reconstruction

• V. Conclusion

This research aimed at proving analogue wavelet transform generation in the dynamics of rational maps. The information from the computer generated picture is hidden in the corresponding continuous wavelet. We have modeled the imaginary part of sample II using the real part of sample I and sample II as the inputs to the artificial neural network with thirteen hidden nodes. We have first imported the ANN model from Tiberius Predictive modelling software to Matlab workspace then from the latter to Matlab SPTool. The filtering process has eliminated noise successfully and generated a modulated signal representing a continuous wavelet. We have also found that the filtered imaginary part of sample II has dominating frequency at half of the sampling frequency. We have explored the continuous wavelet generated using autoSIGNAL software. The model has generated Morlet, Paul and Gaussian derivative mother wavelets. Wavelet Transform provides multiscale information and thus is an efficient tool for local analysis of non stationary signals, especially for processing biomedical signals.