Анизотропные космологические модели типа Бианки I, V, IX в теории гравитации с неминимальной кинетической связью

Благодаря стремительному развитию наблюдательной космологии в последние десятилетия, некоторые астрономические наблюдения говорят нам, что общая теория относительности нуждается в модификации и одним из способов это включение дополнительной степени свободы. Одним из претендентов па. эту роль является скалярное поле, называемое ипфлатопом. На данный момент, существует достаточное количество скалярно-тензорных теорий описывающих эволюцию пашей вселенной. Мы же в качестве рабочей теории сосредоточимся на. теории гравитации с неминимальной кинетической связью [1]. Данная теория является частным случаем более обобщенной скалярно-тензорной теории Хоридески, которая допускает уравнения поля не выше второго порядка. [2].

“Работа выполнена в рамках Программы стратегического академического лидерства «Приоритет 2030» Казанского федерального университета и частично поддержана грантом РИФ № 21-12-00130.

Также известно, что однородная изотропная вселенная Фридмана, включает себя три модели с различным знаком кривизны к = — 1,0,1, что соответствует открытой, плоской и закрытой моделям вселенной [3]. В качестве обобщения открытой, плоской и закрытой вселенной соответствуют модели Бианки типа. V, I и IX соответственно [4]. Изотропные космологические модели хорошо изучены [1], И, [6], поэтому в данной работе мы исследуем поведение анизотропии в однородных космологических моделях на. ранних и поздних стадиях эволюции вселенной.

1. Анизотропные космологические модели в теории с неминимальной кинетической связью

Теория гравитации с иемииимальиой кинетической связью определяется следующим действи ем:

5 =

[9^ЦУ + aG цy ^ Ц>^ _v ф),

(1.1)

где R - скаляр Риччи, д_ЦУ - метрический тензор, G_ЦУ - тензор Эйнштейна, 4/р = 8^, и о -коэффициент неминимальной кинетической связи. Более детальный анализ уравнений поля в ковариантном представлении представлен здесь [5].

Для анизотропных моделей моделей типа. Бианки возьмем метрику, заданную через 1-формы:

ds ² = —dt ² + O 2 W ¹ 0 w¹ + o2w² 0 ш ² + o3w³ 0 w ³ ,

(1.2)

где щ(Д - масштабньie факторы, w¹ - 1-фор мы, где г = 1, 2, 3. Чтобы перейти в определенный тип Бианки используются коммутационные соотношения для 1-форм ш¹. Для модели Бианки I коммутационное соотношение выглядит следующим образом dw^l = 0, для Биаики V — dw¹ = w¹ Л w¹, и для Бианки IX — dw¹ = — 2е^г ^ ^киР Л ш^к.

Таблица 1. Значения в диагональной матрице представляющие кривизну пространства-времени. Где t означает тип Бианки I,V или IX. Также для типа Бианки IX допускаются следующие комбинации {i,j, к} = {1, 2, 3}, {2, 3,1}, {3,1, 2}.

К2 ЦУ	к Цу	к v ЦУ	к1Х ЦУ
К 2 ^ 00	0	—“1	1 [ 2   1    2  1 _2__ “1  _ “2  _ “2 1 з  п 2 +n2 +n3    „2П3    n2n2    п2п2 3 | “ -J      “2     “2      “ 2 “ 3     “ 1 “ 3     “ i “ з J
К2 11	0	—“1	_ 3о2   ।     “2     ।    “к   _ 2   ,    2   ,  _2_ 0202 + а2а2 + а2а2    а2 + а2 + а2 3 к        г к         г 3        г         3        к

Опираясь па. классификацию Бианки получим уравнения поля для этих моделей. Варьируя действие с неминимальной кинетической связью (1.1) по метрике (1.2) и используя следующую параметризацию й ₁ = ae^+^^^-j й ₂ = ae^+ ^— ^З-, 03 = ae^-2^+, г де a - средний масштабный фактор, а р± - параметры анизотропии. Тогда получим следующую систему уравнений после нескольких алгебраических манипуляций

3м^2_г (^{я2 —} ф+ ^— р— ^{+ К}0о) ⁺ ^а^ф2 ^я^{2 — р}+ ^— р— ⁺ зя0о^ = 2 ^{ф 2}, (1.з) Дз It Ч^МР1 + 1 оф²) а³Р+1 = ¹ (м^ — ¹ оф²)(К^1 + ^22 — 2^) , (1.4) a dt 2 о 2

4 Pt \(^МР^{1 +} |^оф 2) a³^1 = ДД C^VP ^— ф°^ф 2) ^(КИ ^{— К}22). (1.5) a dt 2 о \ 2

И варьируя действие (1.1) по скалярному полю ф, получим уравнение на скалярное поле

4 4 {a³ф [1 — a³ dt

3о (я² — р + —р— + А0о)] } = 0.

(1.6)

Перепишем полученные уравнения поля в соответствие с каждым типом Бианки для большей наглядности.

Бианки I

Модель типа. Бианки I в деталях проаиализироваиа и исследована, в данной работе [7]. Ключевым здесь является то, что мы сразу можем получить первые интегралы из этих уравнений (1.8, 1.9).

3(“ + 2“ф2J (н 2 — 3 + — 3-)	= 1Ф2, 2^ ’	(1-7)
1 1 [(“Р+2 “Ф 2) -’3±]	= 0 ,	(1-8)
^1 ^ [1 — 3“ (Н2 — 3+ нз- )]}	= 0.	(1-9)

Бианки V

В модели Бианки V присутствует педиагопальпое модифицированное уравнение Эйнштейна.

01/10

2Н1 - Н 2 — Н з = 0,

(1.10)

что в некоторой степени упрощает систему, так как можно это уравнение проинтегрировать й2 = а₂а₃. И это дает нам 3 = 3 - = — 3 + / V3,

зм 2 [н 2	—432—4 3      а2		+ -“Ф2 [н 2		4 и — 3 2	—	1 3a2		=       2 ,	(1.11)
			1 d a3 dt	(“Р	1 + 2“Ф	2)	a3	• 3	= 0,	(1-12)
	1 d ( 3 1 а Ф a3 dt [	1	— 3“	( н 2 —	432 — 33	1 a2	у		= 0.	(1-13)

В данной модели также как и в Бианки I можно сразу получить первые интегралы (1.12, 1.13), что значительно упрощает дальнейший анализ.

Бианки IX

Некоторый анализ данной модели представлен в данной работе [8]. Стоит заметить, что здесь также имеется первый интеграл (1.16), однако только для уравнения на. скалярное поле.

ам^ Н2 — 3+ — 32 + - +-“Ф2 Н2 — 3+ — 3- +      =  хФ2,                 (1.14) a     2                       3a         2 1 £ [(“Р + 2“Ф2) а33±]  =  2/2 (“Р — 3»2) /3±,(1.15) а? -в {a3» [1—3“ (н 2—3+—3-+К )]j  =  0-                   (1лб> где мы ввели анизотропный потенциал

К = — 1 е-8/3+ (4е6/3+ cosh2(V33-) — 1) (4е6/3+ sinh2(V33-) — 1) .             (1.17)

Для того, чтобы проанализировать данную модель, мы полагаем, что параметры анизотропии 3± <<  1. Тогда раскладывая ан изотропный потенциал К (1-17) по малым 3± вплоть до первого порядка, уравнение (1.15) примет следующий вид

¹ (I “^Мр¹ + ¹ “Ф 2) ^а3³± = 0                          (^1Л8^

1 dt \         2 J

Это позволяет нам получить первый интеграл для параметров анизотропии 3±-

Численные решения данных систем уравнений представлены на. графиках (Рис. 1, Рис. 2). Отсюда видно, что при а /то параметр Хаббла Н ^ 0, это означает, что модели типа Бианки I, V, IX изотропизуются на. поздних стадиях эволюции вселенной. Однако совершенно иначе ведет себя параметр Хаббла Н в этих моделях при а ^ 0.

Рассматривая случай пулевых параметров анизотропии р± = 0 (Рис. 1),в модели типа Бианки I параметр Хаббла Н стремится к константе заданной начальными условиями при численном решении. Это детально исследовано здесь [7]. При а ^ 0 в моделях типа Бианки V и IX параметр Хаббла Н имеет следующие ассимптотики Н ^ +то и Н ^ —то соответственно, что четко видно на. правом графике (Рис. 2).

В случае р± = 0 (Рис. 2) слева, поведение аналогично тому, что и в изотропном случае. Однако, анизотропия дает некоторый вклад в эволюцию вселенной в виде пика, после плато.

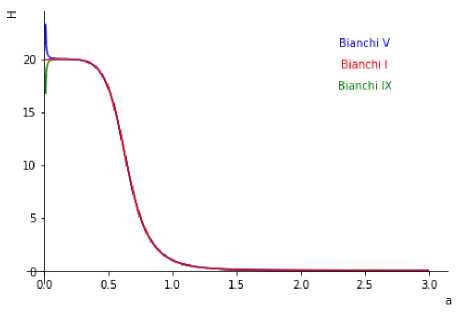
Рис. 1.

Поведение параметра Хаббла Н2 от среднего масштабного фактора а пр и Р± = 0.

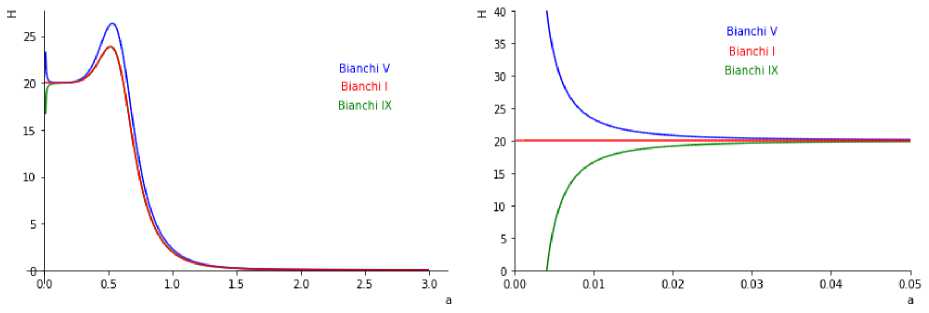
Рис. 2. Поведение параметра Хаббла Н ² в зависимости от а пр и Р± = 0 (Слева). Поведение параметра Хаббла Н² в зависи мости от а пр и Р± = 0 вблизи пуля. (Справа)