Ant Colony Optimization for Train Scheduling: An Analysis

Published Online January 2014 in MECS

Ant Colony Optimization (ACO) is a meta-heuristic technique and is used to find shortest path between source and destination. ACO is widely used in scheduling and routing problems. J. E. Bell and P. R. McMullen [1], B. Bullnheimer, R. F. Hartl, and C. Strauss [2] solved the vehicle routing problem by Ant Colony Optimization. It is also applied for solving NP-hard problems like traveling salesman problem [3-5], scheduling problem [6], water distribution problem [7], sequential ordering problem [8], etc.

In Indian Railway scenario [9] [10], all type of trains Mail, Passenger, Express, Superfast and Cargo runs on same track. The total area is divided into zones and zones are divided into divisions. There are several tracks available to reach from one zone to another through different divisions. Moreover, within the divisions the numbers of tracks are limited and the numbers of trains are more. So proper scheduling is required to be maintained to optimize the cost (possibly in terms of time). Generally, in India the scheduling of cargo trains are maintained on the basis of priority and Shortest Job First (SJF) and for the free traffic First Come First Serve (FCFS) is used which is termed as Standard Train Scheduling (STS) [9].

Optimization techniques can be applied to solve train scheduling problem effectively. Cai and Goh [11] solved the train scheduling problem by heuristic method and found satisfactory result. Khairnar [12] designed a decision support system for scheduling a new train. Keivan and Fahimeh [13] solved the train scheduling problem using ACO and shown some improving results. They have considered scheduling on single track with uniform speed. Here we have tried to overcome the limitation of uniform speed. The recent paper [14-16], considers variable speed on single track but lacks the collision detection and avoidance criteria. We have considered collision free single track cases on different positions of trains to retain the complexity of the problem as double track can pass two trains at a time without collision.

We have considered four different possible conditions namely (a) same speed (b) different constant speed (c) maximum speed limit condition and (d) variable speed; for both the trains moving in same as well as different directions.

The paper is organized as follows: Section 2 describes the basics of Ant Colony System. Section 3 deals with the design principles of train scheduling on single track. Section 4 demonstrates the experimental setup. Section 5 deals with the results and discussions and Conclusions are drawn in Section 6.

• II.    Background

• 2.1    ACS (Ant Colony System) State Transition Rule

Ants deposit special chemical called pheromone on the ground and objects. Behavior of all ants is essentially influenced by the pheromone which they detect in their way. Ants use different levels of pheromones to coordinate every activity which their colony needs. The pioneer ant randomly explores the environment for the food source. When it finds the food source it returns to the nest depositing a variable amount of pheromone which is proportional to the richness of the food source. Other ants choose their movement probabilistically with preference of places with higher amount of pheromone. The slowly evaporating nature of pheromone decreases the amount on unused as well as less frequently used paths. Their way of communication via pheromone to choose the shortest path is termed as Ant Colony Optimization (ACO) technique.

Bonabeau [17] have shown that Linepithema humile, an ant species use recruitment to efficiently organize the foraging behavior of the ant colony. A simple experiment was performed with two bridges of different lengths placed between the ants’ nest and a source of food (Fig. 1). Initially the random paths chosen by the ants and their probability of choosing each bridge is 0.5. However as time passed, and the pheromone trails increased, the ants intended to favor the shortest route to the food. The pheromone trail increased on the shorter bridge with respect to time because the ants consume less time to cover the distance, and in turn population of ants increased on the shorter path.

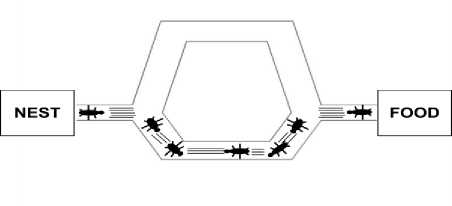
Fig. 1: An illustration of the original (biological) ant experiment

There are different variations of ACO. Out of them ACS (Ant colony System) is one of the most successful technique which uses state transition rule to choose the next move and local as well as global updates to determine the efficient paths.

Ants prefer to move from one place to another (i.e. one node to other node) which are connected by short edges with a high amount of pheromone [18]. It can be done by using following rule.

An ant positioned on node r chooses the city s as to move by applying the rule given by (1).

PIk (r, s ) = “

z

T (r, s ). Щ ( r, s )]в T ( r, u ). Щ( r, u )] в

if se Jk (r),u e Jk (r)

otherwise where τ is the pheromone, η =1/d is the inverse of the distance d (r,s), Jk(r) is the set of cities that remain to be visited by ant k positioned on city r (to make the solution feasible) and ß is a parameter which determines the relative importance of pheromone versus distance (ß >0). Equation (1) multiplies the pheromone on edge (r,s) by the corresponding heuristic value η (r,s). In this way we favor the choice of edges which are shorter and which have a greater amount of pheromone.

• 2.2    ACS Local Updating Rule

• 2.3    ACS Global Updating Rule

While building a solution (i.e., a tour) of the TSP, ants visit edges and change their pheromone level by applying the local updating rule [9] of Eq. (2):

t(r,s) ^(1 -p)*t(r,s) + рЛт(r,s)     (2)

where 0< p <1 is a parameter.

We have assumed ∆ τ(r, s) = τ₀.

Once all ants have built their tours, pheromone is updated on all edges by using the following rule :

t (r, s ) ^(1 - a )*t ( r, s ) + «.At ( r, s )     (3)

where 0<α<1 is pheromone decay [19-20] parameter and we assume α=0.2 to get a better effect of probability on the globally shortest path.

Where,

(Lg6)    if (r, s )e global best0       otherwise and Lgb is length of globally best tour.

• III.    Design on Single Track

• 3.1    Same Speed for Both Trains

The different possible conditions according to the position of the trains are discussed bellow:

T ( r , s ) = <

Let assume there are two trains T1 and T2 between two stations S1 and S2 and every station has two platforms P1 and P2, where D is departure time of train T, A is arrival time of train T, H is headway time of trains T1 and T2.

Condition 1: If trains are moving from station S1 and S2 in opposite direction then departure time should maintain the following equation:

D{T2,S2}=>A{T1,S2}+H{T1,T2}           (4)

or D{T1,S1} = >A{T2,S1} + H{T1,T2}

Equation (4) shows that departure time of second train from station S2 should be equal to or more than arrival time of first train at station S2 plus headway time of first and second train, or departure time of first train from station S1 should be equal to or more than arrival time of second train at station S1 plus headway time of first and second train.

Condition 2: If both train are moving in same direction from any station S1 or S2, then allow departing the trains in difference of its headway time which should be more than 20 min (assumed).

D{T2,S}=>H{T1,T2}+D{T1,S}             (5)

or D{T1,S} = >H{T1,T2} + D{T2,S}

Equation (5) shows that departure time of second train from one of the stations should be equal to or more than departure time of first train at same station plus headway time of first and second train, or departure time of first train from one of the stations should be equal to or more than departure time of second train at same station plus headway time of first and second train.

• 3.2    Different Constant Speed for Both Trains

Condition 1: If two trains T1 and T2 are moving in opposite direction from stations S1 and S2 and speed (T1) > speed (T2), then train T1 should be allowed to move first on the track and T2 should start after T1 passes.

D{TS,S1}=>A{TF,S2}+H{TS,TF}          (6)

or D{TS,S2} = >A{TF,S1} + H{TS,TF}

Equation (6) shows that departure time of slower train from station S1 should be equal to or more than arrival time of faster train at station S2 plus headway time of slower and faster train, or departure time of slower train from station S2 should be equal to or more than arrival time of faster train at station S1 plus headway time of slower and faster train.

Condition 2: If both trains are moving in same direction from any station S1 or S2, then we have to check the speed of both trains and allow faster train to go first and after that slower train to go on track in difference of its headway time.

D{TS,S}=>D{TF,S}+H{TS,TF}               (7)

Equation (7) shows that departure time of slower train from any one of station should be equal to or more than departure time of faster train from same station plus headway time of slower and faster train.

• 3.3    Maximum Speed Limit Condition for Both Trains and at Fixed Speed

Condition 1: If two trains are moving in opposite direction then let the faster train go first and slower train later but the fastest speed of the both train should be less then fixe speed on track.

• (i)    D{TS,S1}=>A{TF,S1}+H{TS,TF}(8)

and   Sp{TS,TF}< Sf

• (ii)    D{TS,S2} = >A{TF,S2} + H{TS,TF}

and   Sp{TS,TF}< Sf

Case (i): Equation (8)-(i) shows that departuretime of slower train from station S1 should be equal toor more than arrival of faster train on station S1 plus headway time of slower and faster train but maximum speed of slower and faster train should be less then fixed speed at all the time when trains are moving on the track.

Case (ii): Equation (8)-(ii) shows that departure time of slower train from station S1 should be equal to or more than arrival of faster train on station S1 plus headway time of slower and faster train but maximum speed of slower and faster train should be less then fixed speed at all the time when trains are moving on the track.

Condition 2:  If two trains are moving in same direction then let the faster train go first and slower train later by the difference of there headway time but the fastest speed of the both train should be less then fixe speed on track.

D{TS,S}=>D{TF,S}+H{TS,TF}          (9)

and Sp{TS,TF} < Sf

Equation (9) shows that departure time of slower train from any one of station should be equal to or more than departure time of faster train from same station plus headway time of slower and faster train but maximum speed of slower and faster train should be less then fixed speed at all the time when trains are moving on the track.

• 3.4    Variable Speed for Both Trains

Condition 1: If two trains T1 and T2 are moving in opposite direction between stations S1 and S2 on track then check the average speed of both trains by the sensors which are applied on the track and let the faster train go first

D{TS,S1}=>A{TF,S1}+H{TS,TF}         (10)

or D{TS,S2} = >A{TF,S2} + H{TS,TF}

Equation (10) shows that departure time of slower train from station S1 should be equal to or more than arrival of faster train on station S1 plus headway time of slower train and faster train, or departure time of slower train from station S2 should be equal to or more than arrival of faster train on station S2 plus headway time of slower train and faster train.

Condition 2: If two trains T1 and T2 are moving in same direction between stations S1 and S2 on track then second train T2 should have less speed then first train T1 at all time on the track or there should be more than 3 km distance between trains T1 and T2.

• (i)    D{T2,S1}=>D{T1,S1}+H{T1,T2}        (11)

and DS{T1,T2} = > 3 K.M.

or      Sp{T1} = > Sp{T2}

• (ii)    D{T2,S2} = >D{T1,S2} + H{T1,T2}

and DS{T1,T2} = > 3 K.M.

or      p{T1} = >Sp{T2}

Case (i): Equation (11)-(i) shows that departure time of second train from station S1 should be equal to or more than departure time of first train from station S1 plus headway time of first and second train, And distance between first and second train on track should be equal to or more than 3 km or speed of first train should be always more than speed of second train on track.

Case (ii): Equation (11)-(ii) shows that departure time of second train from station S2 should be equal to or more than departure time of first train from station S2 plus headway time of first and second train, And distance between first and second train on track should be equal to or more than 3 km or speed of first train should be always more than speed of second train on track.

• IV.    Simulation Experiment

For the sake of understanding an example graph Graph1 in Fig. 2 is considered. The nodes are considered as zones. There are several paths possible to reach from one zone to another zone. The scheduling between the zones are considered only because in each division have a limited tracks which bound the trains to follow the same path on time sharing basis. Here Node1 is the starting station and Node 6 is the destination station and each station has at least two platforms. The distances between the stations are assumed (not real distances) in km.

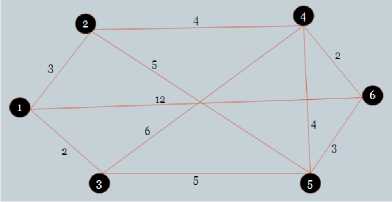
Fig. 2: Graph 1

The program was written in C language in AMD Opteron 2.2 GHz machine with x86 64 architecture having 2 GB RAM. We have also considered another four cases as shown in Fig. 3, 4, 5 and 6 respectively as shown in matrix form for the respective graphs.

12 3 4 1 Ло 4 5 О 2 4 0 0 6

3  5 0 09

4  0 6 90

5  9 7 34

5 6

9 О

7 О

3 О

4 5

О 2

2 О

6'0 005

• Fig. 3:    Adjacency matrix of Graph 2

  1 2

  
  

3 4 5 6

5 0 0 9'

0 2 4 0

0 3 7 5

3 0 6 0

7 6 0 6

5 0 6 0>

• Fig. 4:    Adjacency matrix of Graph 3

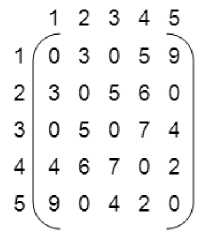
Fig. 5: Adjacency matrix of Graph 4

3 4

5 14

9 9

О 8

8 О

Fig. 6: Adjacency matrix of Graph 5

The ant colony system is applied on different Graphs. The step by step process for Graph 1 is described below:

Step1: Trains are allowed with time constraints and priority. Populate sufficient amount of ants (> S² i.e. greater than square of no of stations S) at the starting node (say 1).

Step2: Apply state transition rule to choose the next move to the adjacent stations.

Step3: Perform local update.

Step4: Store the paths from source to destination by applying Step 3 & Step4 repeatedly till the destination reaches.

Step 5: Apply global update on the best path out of three stored paths.

Step 6: Repeat above steps till all ants converge in the shortest path or a maximum number of ants (80%) converge in the shortest path.

Step 7: Store the best path along with other two alternate promising paths from the results from the iterations done so far.

Step 8: Check the conditions as discussed in Section 3 for the best path for each station pair and set the departure time accordingly fulfilling the time constraint.

Step 9: If the best path is blocked due to some reason, schedule the train in the next alternate promising path after checking the time constraint and priority.

• V.    Simulation Results

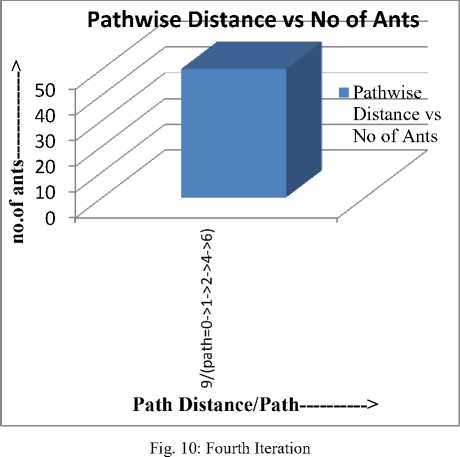
  The assumptions and conditions for the implementation were taken from Operational Manual [16] of Indian Railways. After successful implementation of our algorithm, we have checked iteration wise convergence of the ants to obtain the best path. Total number of ants considered is 50 for Graph 1. At the end of the first iteration, all promising paths and number of ants through those paths are explored. The concentration of ants on a particular path depends on the distance. In the first iteration 6 ants chooses the shortest path (i.e. 1246) followed by 8, 15 and 50 ants in consecutive iterations as shown in Fig. 7, 8, 9 and 10. Number of paths retained iteration wise is inversely proportional to the distance because ants do not prefer

their movement on relatively larger paths as the concentration of pheromone decreases on those paths.

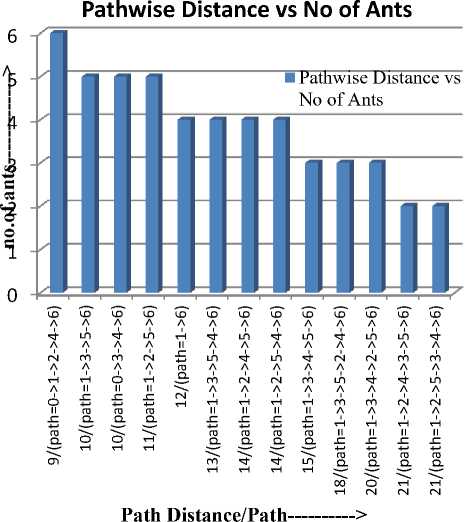
Fig. 7: First Iteration

After first iteration, consecutive iterations are continued till all ants or maximum (80%) ants converge in the shortest path. It is observed that less number of path are traversed by the ants.

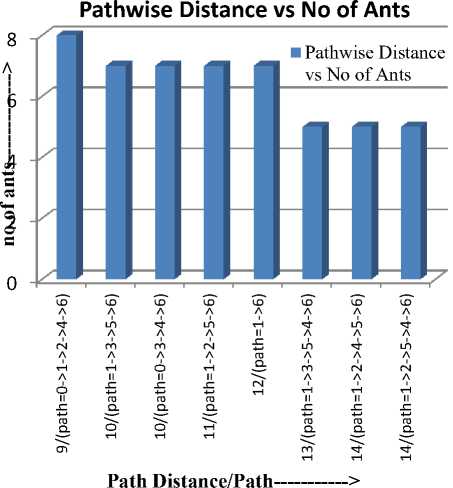
Fig. 8: Second Iteration

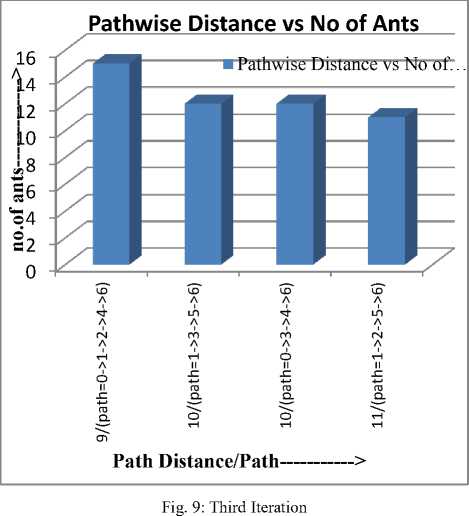
In third iteration there are four more paths are skipped and in fourth iteration all ants are moving in shortest path.

The proposed Train scheduling algorithm is compared with the Standard Train scheduling algorithm in a single track scenario and it is assumed that on each station one platform is blocked by a cargo train. We have considered five cases with variable number of links as well as nodes and traced the execution time for the both algorithm as shown in Table 1. Number of paths denotes the available paths for source destination pair.

The time is traced iteration wise. First iteration takes 10.15 milliseconds whereas second, third and fourth iteration takes 5.93, 3.03 and 2.37 milliseconds respectively as shown in Fig. 11.

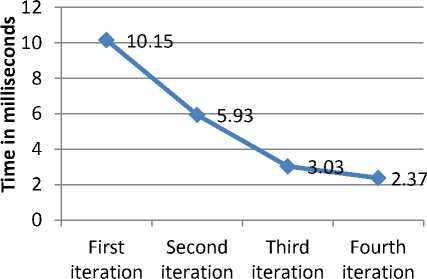
Fig. 11: Iteration wise execution time

Table 1: Comparison of Execution Time for Ant Colony Optimization Train Scheduling (ACOTS) and Standard Train Scheduling (STS) on Different Graphs

Graph	No of Links	No of Nodes	No of Paths	Execution time of ACOTS(milli-sec)	Execution time of STS(milli-sec)
1	10	06	13	23.54	46.27
2	10	06	16	28.07	46.27
3	10	06	12	19.93	46.27
4	08	05	07	16.66	33.54
5	06	04	05	12.72	22.97

From the simulation results it is observed that our proposed Ant Colony Optimization Train Scheduling (ACOTS) takes less time than the Standard Train Scheduling (STS) and hence performance is better. It also takes care of collations to avoid accidents as discussed in Section 3.

The graphical representation of Table 1 is shown in Fig. 12 as shown below:

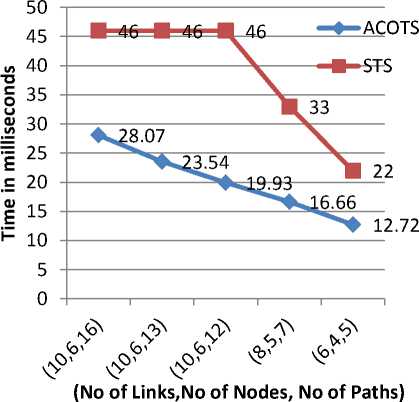
Fig. 12: Graphical view for comparison between Ant Colony Optimization Train Scheduling (ACOTS) and Standard Train Scheduling (STS) Algorithm

• VI.    Conclusion

Finally we conclude as under:

• (i)    Cargo train scheduling is one of the important problems as these trains generate huge revenue for the Railway Department.

• (ii)    The technique used for the solution is bioinspired and capable to solve highly combinatorial problems.

• (iii)    From the results in Section 5, it is evident that proposed Ant Colony Optimization Train Scheduling (ACOTS) exhibits better performance than the Standard Train Scheduling (STS).

• (iv)    Proposed algorithm is capable to produce alternate paths which may be useful for time bound situations or sudden damage on paths.

• (v)    The algorithm facilitates safe, collision free journey.