Anti-Swing and Position Control of Double Inverted Pendulum (DIP) on Cart Using Hybrid Neuro-Fuzzy Controllers

Published Online July 2016 in MECS

Inverted Pendulum (IP) is one of the complex, highly non-linear and multi-variable system [1], [2]. It is widely used as laboratory model for practical implementation and demonstration of various control systems. Various Soft computing techniques "Ref. [3]" have been used for Stabilization of IP systems. Chen et al. [4] designed a neural network controller based on two stage chaos optimization algorithm for DIP system. The controller was able to solve local minimum problem one of the disadvantage of Back-propagation (BP) neural networks. Xiu-fen at al. [5] proposed a controller based on BP algorithm of Artificial neural network (ANN) having 4 input and 3 layer structure for IP system. The ANN controller was further compared with fuzzy logic controller. J. Yu et al. [6] proposed a LQR controller for control of Linear double flexible inverted pendulum system. The LQR controller was further used to design an efficient neural network controller based on Sugeno-type fuzzy inference system. The simulation results proved that neural controller was better as compared to LQR controller in terms of speed, stability and accuracy.

Yi-Jen and Min [7] designed an Adaptive terminal sliding mode recurrent fuzzy neural network (ATSRFNN) to control a coupled DIP system. The ATSRFNN controller was composed of a recurrent fuzzy neural network (RFNN) and an adaptive terminal sliding (ATS) controller. The RFNN controller was designed to mimic an ideal controller and ATS controller controls the external disturbances. Fujinaka et al. [8] proposed a Neuro-PID control architecture to stabilize DIP system. The gain parameters of PID controller were tuned using neural networks. The simulation results shows the effectiveness of the proposed control architecture. Sang at al. [9] performed the control of DIP with improved BP algorithm of ANN. The BP network of 6-10-1 structure was used for learning. In "Ref. [10]" a locally linear neuro fuzzy (LLNF) approach for building an inverse model for friction compensation of DIP has been proposed. Sang et al. [11] proposed an artificial neural network (ANN) with improved BP algorithm for balance control of double inverted pendulum system. The training data for ANN was acquired from three-loop PID algorithm. The BP network of 6-10-1 structure with Tansig function in the hidden layer and Purelin function in the outer layer was used.

In "Ref. [12]" an experimental study on decentralized neural network to control a 2-degree of freedom inverted pendulum on an x-y plane has been performed. The neural controllers were applied to control both angle and position of the cart. Fuyan Cheng et al. [13] designed a high accuracy and high resolution fuzzy controller to stabilize a DIP at upright position. They combined fuzzy control theory with optimal control theory to determine composition coefficients. Lee and Jung [14] proposed a Takagi-Sugeno (T-S) Neuro fuzzy control scheme to control IP system. The BP learning algorithm for the T-S neuro fuzzy network was derived for on-line learning and control. Xiao et al. [15] presented a motion mode control for double inverted pendulum system based on fuzzy logic and neural network. The parameter of neural controller were optimized by back propagation algorithm. Further, the motion modes of the system were defined and adjusted online. Experimental implementation and testing proved the validity of proposed methodology. This study shows a comparison analysis of two different soft-computing approaches for control of DIP on cart. Initially fuzzy logic controllers (FLC's) were used for the control of DIP systems. The data sets from FLC's were used for training of NN's controllers. The modeling and simulation of the complete system and sub-system were done in Matlab-Simulink. The results proved the validity of the proposed techniques.

Equation's of motion for Cart

̈= (F- -b ̇)

• II.    DIP on Cart

DIP consists of two inverted pendulums mounted on cart which is free to move along horizontal direction. The cart has to be controlled by an input force F. A view of DIP is shown in fig.1. "Ref. [16]". It's dynamics represents a two-link kinematic joint for Robotic arm, robotic knee, multi-stage rocket etc "Ref. [17]". The objective is to control the DIP system such that angle of bottom pendulum ( ), angle of top pendulum ( ), and cart position (x) should be equal to zero. A view of various input parameters for DIP system are shown in table 1.

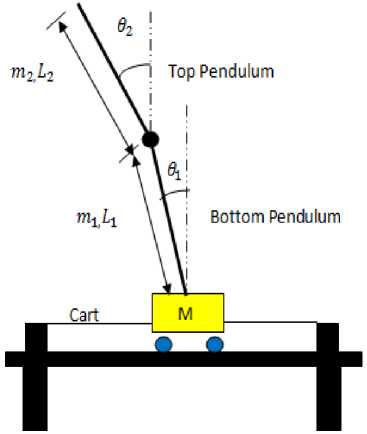
Fig.1. Double Inverted Pendulum on cart

Table 1. Input parameters of DIP system

Symbol	Parameter	Value	Unit
M	Mass of Cart	2	Kg
m -	Mass of Bottom Pendulum	1	Kg
m 2	Mass of Top Pendulum	0.5	Kg
L -	Length of Bottom Pendulum	0.1	m
L2	Length of Top Pendulum	0.1	m
I	Moment of inertia	0.006	kgm²
g	Acceleration due to gravity	9.8	m/s²
b	Coefficient of friction	0.1	Ns/m²

• III.    Mathematical Equations

The Matlab-Simulink model for DIP was derived using Newton's Second law. The governing equations for subsystems were derived as follows.

Equation's of motion for Bottom Pendulum

= (     cos + sin -

̇ +     cos + sin )(2)

P_l = m_L (- 0 1 L ₁ cos 0₁ -0" ₁L _L sin 0_L +g)

+ m₂ (2 0^L ₁ cos 0₁ -2 U_lL ₁ sin 0_l -

022ccos02-02L 2COSH2+g)

=    ( ̈+ ̇ sin - ̈ cos ) + m 2 (x +20 c L Lsin0 l-20lL Lcos 0 l+

̇ sin - ̈ cos(4)

Equation's of motion for Top Pendulum

̈ =  (      cos + sin -    ̇ )(5)

P₂ = m_c (-2 0 ^c L ₁ cos 0₁ -2 0 _l L _L sin 0 _l -

0L2ccos0c-0cLccos0c+g)

=    ( ̈+2 ̇ sin -2 ̈ cos +

+0cL2sin02-02 Lccos0 2)(7)

• IV.    Fuzzy Logic Control of Dip System

Fuzzy logic controller (FLC) is one of the most successful application of fuzzy set theory which involves the application of linguistic variables rather than numerical variables "Ref. [18]". The advantage of using FLC is that it substitute a fuzzy rule based system for a skilled human operator "Ref. [19]". This study used Mamdani fuzzy inference system (M-FIS) having gbell MF's for designing of FLC's. A total of seven linguistic variables were selected. A view of gbell MF's and if-then fuzzy rules for cart controller are shown in fig.2 and table 2 respectively.

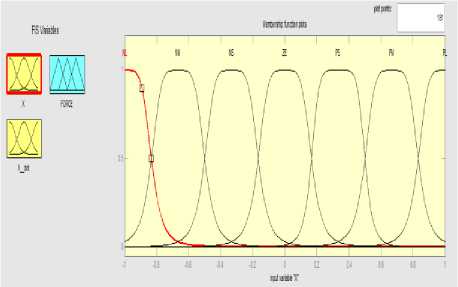
Fig.2. MF's for Cart controller

Table 2. If-then fuzzy rules

FORCE	X
X Dot	NL	NM	NS	ZE	PS	PM	PL
	NL	NL	NL	NL	NM	NS	ZE
	NL	NL	NL	NM	NS	ZE	PS
	NL	NL	NM	NS	ZE	PS	PM
	NL	NM	NS	ZE	PS	PM	PL
	NM	NS	ZE	PS	PM	PL	PL
	NS	ZE	PS	PM	PL	PL	PL
	ZE	PS	PM	PL	PL	PL	PL

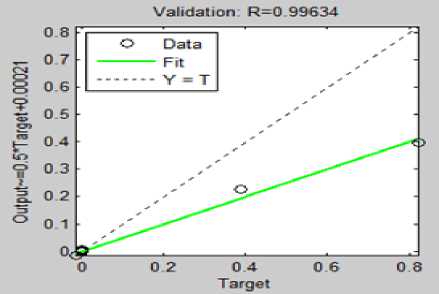
Fig.5. Regression plot Validation data

• V.    Neural Network Control of DIP System

The data sets for NN's controllers were considered from results of Fuzzy controller. A total of 302 data sets were collected which were randomly divided into training, validation and testing samples. The training was done using Levenberg-Marquardt back propagation algorithm and training performance was measured Mean squared error (MSE) method. Training automatically stops when generalization stops improving, as indicated by an increase in MSE of validation samples. A view of neural network control architecture for designing of cart controller is shown in fig.3. It consists of two inputs and one output with 25 neurons in the hidden layer and 1 neuron in the output layer.

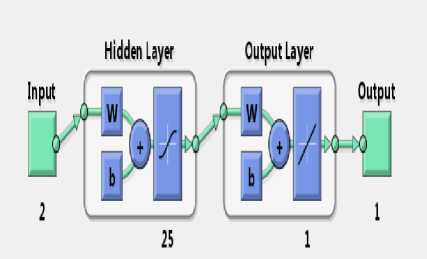
Fig.3. Neural network architecture

The regression plots for training, validation and test data samples for cart controller are shown from fig.4 to fig.6.

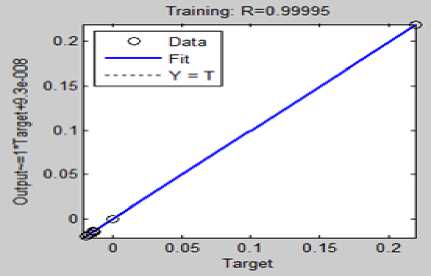
Fig.4. Regression plot for Training data

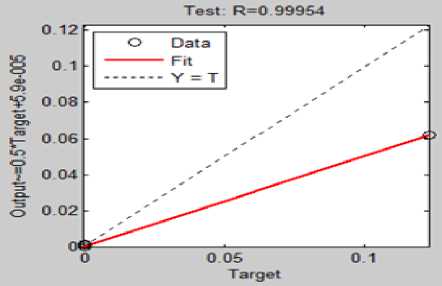
Fig.6. Regression plot for Test data

The different values of R and MSE, for cart, bottom pendulum and top pendulum upto 4 decimal places are shown in table 3.

Table 3. Values of R and MSE for different controllers

Regression values (R)	Cart	Bottom pendulum	Top pendulum
Training	0.9996	0.9999	0.9970
Validation	0.9963	0.9863	0.9671
Test	0.9995	0.9852	0.9969
All	0.9743	0.9957	0.9907
MSE	2.27e-08	0.00413	0.0251

• VI.    Simulink Modeling

The mathematical equations were used for developing Matlab-Simulink model of the DIP system. A DIP subsystem was built which was finally masked to give complete system. A view of Simulink of DIP sub-system and Simulink of DIP are shown in fig.7 and fig.8 respectively.

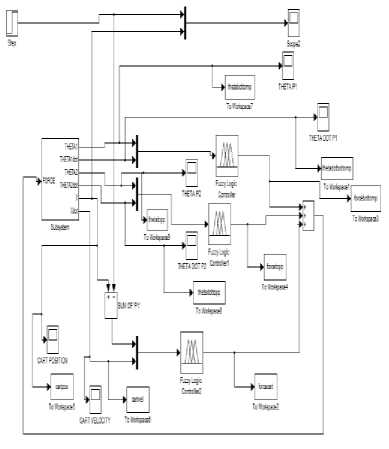
Fig.7. Simulink of DIP system

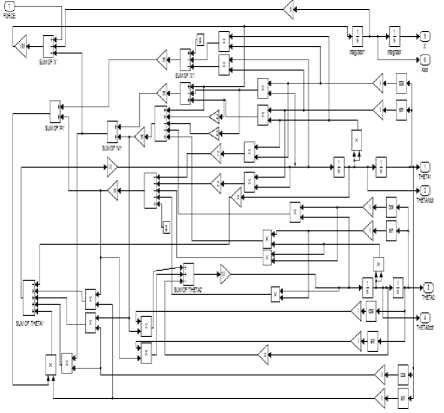
Fig.8. Simulink of DIP sub-system

The Simulation results for fuzzy and NN's controller were shown with the help of graphs and tables below.

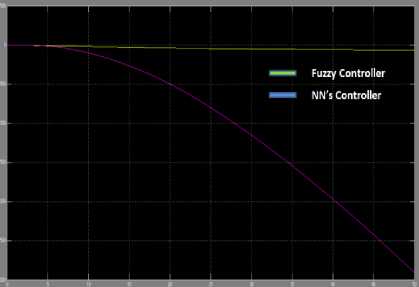
Fig.9. Cart Position control

Table 4. Output responses for Cart position

Performance parameter	Fuzzy controller	NN's controller
Settling time (sec)	5sec	.....
Max. Overshoot (degrees)	60º	.....
Steady state error	0	.....

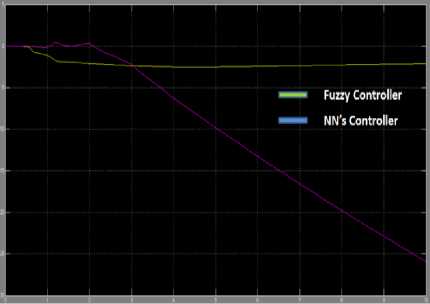
Fig.10. Cart Velocity control

Table 5. Output responses for Cart velocity

Performance parameter	Fuzzy controller	NN's controller
Settling time (sec)	1.2 sec	.....
Max. Overshoot (degrees)	-2.5 º	.....
Steady state error	0	.....

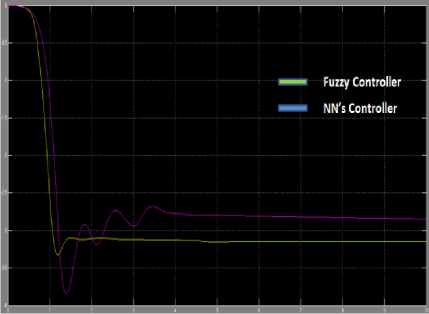
Fig.11. Bottom pendulum angle control

Table 6. Output responses for Bottom pendulum angle

Performance parameter	Fuzzy controller	NN's controller
Settling time (sec)	1.4 sec	3.8 sec
Max. Overshoot (degrees)	-3.3º	-3.7º
Steady state error	0	0

Table 7. Bottom pendulum angular velocity

Performance parameter	Fuzzy controller	NN's controller
Settling time (sec)	2 sec	4 sec
Max. Overshoot (degrees)	1.2º to -8.5º	3.5º to -9.8º
Steady state error	0	0

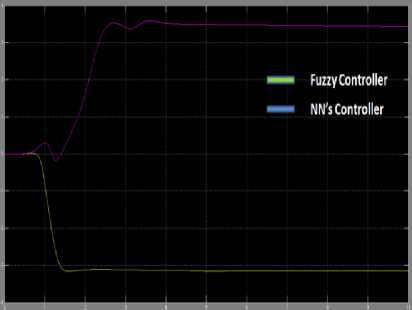
Fig.13. Top pendulum angle control

Table 8. Top pendulum angle

Performance parameter	Fuzzy controller	NN's controller
Settling time (sec)	1.5 sec	3.5 sec
Max. Overshoot (degrees)	0.1º to -3.2º	3.6º to -0.2
Steady state error	0	0

Table 9. Top pendulum angular velocity

Performance parameter	Fuzzy controller	NN's controller
Settling time (sec)	1.5 sec	4 sec
Max. Overshoot (degrees)	0.2º to -7.8º	4.5º to -3.2º
Steady state error	0	0

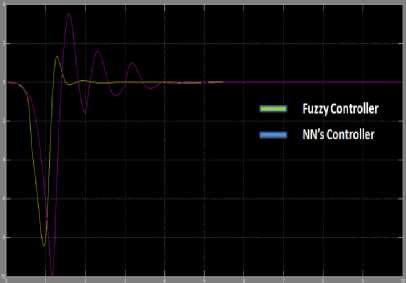
Fig.12. Bottom pendulum angular velocity

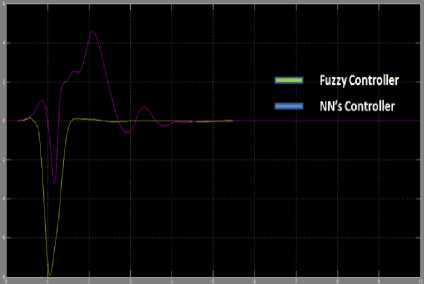
Fig.14. Top pendulum angular velocity control

• VIII.    Conclusion

A comparison study for control of highly non-linear DIP system on cart has been proposed. A fuzzy logic controller was designed which controls the complete system within 2 sec and zero steady state error. The data sets from fuzzy controller were used to train the Neural network controllers using Levenberg-Marquardt method. The Regression and MSE values for NN's controllers were adequate. It was also observed that NN's controller was not able to control cart position and velocity but provides excellent results for pendulum controllers. The maximum overshoot for fuzzy controller were less as compared to NN's controllers. As an extension to future work other methodologies including Genetic Algorithm (GA), Particle swarm optimization (PSO) etc can also be incorporated and compared for control of non-linear systems.