Аппаратная реализация кодирования информации систематическими полярными кодами

Автор: Тимофеев Г.С.

Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau

Рубрика: Математика, механика, информатика

Статья в выпуске: 1 т.18, 2017 года.

Бесплатный доступ

Кодирование информации с помощью корректирующих кодов позволяет осуществлять контроль целостности передаваемых сообщений, а в ряде случаев - исправлять ошибки, возникшие при передаче информации по каналу с шумом. Рассматриваются полярные коды - двоичные линейные блоковые корректирующие коды, достигающие пропускной способности симметричных каналов без памяти. В основе полярных кодов лежит операция поляризации N-разрядного двоичного симметричного канала без памяти. Рассматриваются операции несистематического и систематического кодирования информации полярными кодами с прямым порядком битов и с битовой перестановкой, приводится метод реализации систематического кодирования через двукратное несистематическое кодирование полярными кодами. Вводится операция прекодирования - преобразования K-разрядного информационного вектора в N-разрядный вектор в соответствии с некоторым полярным кодом С. Предлагается схема прекодера, построенная с использованием регистров сдвига, которая позволяет осуществлять прекодирование для любого (N, K)-полярного кода. Приводится обзор вариантов аппаратной реализации несистематических кодеров полярных кодов с прямым порядком битов и с битовой перестановкой и их сравнительные характеристики. Приведенные варианты реализации основываются на конвейерном способе организации вычислений и имеют разрядность входного сигнала P, кратную длине кодового слова N. Предлагается схема систематического кодера (32, 16)-полярного кода с прямым порядком битов, включающая в себя блок прекодера и два блока несистематического кодирования и реализующая конвейерный способ организации вычислений, приводится временная диаграмма конвейера предлагаемого кодера. Рассматриваются варианты масштабирования предлагаемой схемы с целью реализации систематического кодирования полярными кодами с практически значимыми значениями длины кодового слова N. Масштабирование в ширину предполагает увеличение разрядности входного сигнала P, масштабирование в длину предполагает увеличение числа стадий конвейера для каждого блока несистематического кодирования. Приводятся результаты моделирования предлагаемого систематического кодера в пакете Altera Quartus II 13.0 с использованием системы ModelSim 10.1. Результаты полностью совпадают с результатами моделирования в пакете MATLAB R2016b.

Еще

Коды с коррекцией ошибок, полярные коды, систематические полярные коды

Короткий адрес: https://sciup.org/148177696

IDR: 148177696

Текст научной статьи Аппаратная реализация кодирования информации систематическими полярными кодами

Введение. В настоящее время помехоустойчивое кодирование является неотъемлемой частью любой современной системы связи, в том числе космической. Применение помехоустойчивого кодирования позволяет снизить уровень ошибок в передаваемых сообщениях и повысить надежность передачи сообщений.

Полярные коды, предложенные Эрдалом Ариканом, имеют большое практическое значение, поскольку доказано, что они достигают пропускной способности симметричных каналов без памяти [1]. Кроме того, для полярных кодов характерно отсутствие области насыщения ошибок [2] и низкая сложность реализации [3]. Однако полярные коды имеют два существенных недостатка: во-первых, низкую эффективность для коротких кодов и кодов средней длины по сравнению с LDPC-кодами аналогичной длины, а во-вторых, алгоритм последовательного исключения (Successive Cancellation, SC), предложенный Ариканом для декодирования полярных кодов в [1], является последовательным по своей природе, что влечет за собой низкую пропускную способность.

В настоящее время существует ряд методов, решающих эти проблемы. Дальнейшим развитием идеи полярных кодов являются систематические полярные коды [4], позволяющие значительно снизить уровень битовых ошибок в передаваемых сообщениях. Для повышения эффективности полярных кодов был предложен ряд новых алгоритмов декодирования, развивающих идеи SC-декодирования [5–7]. Также был предложен ряд решений, повышающих пропускную способность алгоритмов декодирования [8; 9].

В статье представлен обзор существующих подходов к аппаратной реализации кодирования полярных кодов. Выделена и подробно рассмотрена операция прекодирования – предварительного преобразования информационного сообщения длины K в сообщение длины N , предложен вариант аппаратной реализации. Разработано устройство систематического кодирования полярными кодами, включающее в себя блок, реализующий операцию прекодирования.

Кодирование полярными кодами. Полярные коды относятся к классу двоичных линейных блоковых кодов. В основе процедуры кодирования полярными кодами лежит операция поляризации канала, которая описывается линейным преобразованием, задаваемым матрицей F ® n , где F - 2 x 2 — ядро поляризации,

F =

1 I ; 0 n - n -кратное кронекеровское произ-матрицы с собой; n = log 2 N , где N – длина

ведение

кодового слова конструируемого кода. Полярный код С задается набором параметров ( N, K, A c ), где N – длина кодового слова; K – размер информационной части; A c – множество «замороженных» символов, значение которых равно нулю, \A_c\ =N-K , A c с {0,..., N - 1}. Методы построения полярных кодов подробно рассмотрены в [1; 10].

Несистематическое кодирование полярными кодами описывается выражением xN = uNGn , (1)

где x ₁ ^N – кодовое слово; u ₁ ^N – вектор, включающий информационные символы ( u i t A c , 1 < i < N) и «замороженные» позиции ( u i e A c , 1 < i < N); G N - порождающая матрица полярного кода, задаваемая матри- F® n

. Если порождающая матрица задается выражением

G n = B n F ⁰ ⁿ , (2)

где B N – матрица перестановки, то код называется полярным кодом с битовой перестановкой (bit-reversed) [1]. Если порождающая матрица задается выражением

G n = F ® ⁿ , (3)

то код называется полярным кодом без битовых перестановок (non-reversed) [4]. Схемы bit-reversed и nonreversed (8, 5, {1, 3, 5})-полярных кодов представлены на рис. 1.

Систематическое кодирование. Систематическое кодирование позволяет не изменять значения информационных битов. Кроме того, оно позволяет значительно снизить уровень битовых ошибок [4]. Процедура кодирования описывается выражением xN = yNG, (4)

где G_N может соответствовать как выражению (2), так и выражению (3).

В векторе x 1 N значения x i t A c равны значениям информационных битов, а значения x i e A c неизвестны. В векторе y N значения y i e A c равны нулю, y i t A c неизвестны. После решения уравнения (4)

вектор x ₁ является кодовым словом систематического полярного кода. Алгоритмы программной реализации систематического кодирования полярными кодами подробно рассмотрены в [11]. Рис. 2 иллюстрирует операцию систематического кодирования non-reversed (8, 5, {1, 3, 5})-кодом.

Для bit-reversed полярного кодирования операция систематического кодирования аналогична, за исключением соединения элементов «исключающее ИЛИ», которое соответствует рис. 1.

В работах [12; 13] рассматривается метод реализации систематического кодирования полярными кодами через двукратную операцию несистематического кодирования. Для этого необходимо:

1) преобразовать информационное сообщение d ₁ ^K в сообщение u ₁ ^N в соответствии с Ac ;
2) осуществить процедуру несистематического кодирования над вектором u ₁ ^N , получить вектор x ₁ ′ ^N ;
3) обнулить символы x_i ′ ∈ A_c ;
4) осуществить процедуру несистематического кодирования над измененным вектором x ₁ ′ ^N , полу

_N чить вектор x1 .

На рис. 3. представлена схема систематического кодирования на основе несистематического non-reversed кодирования.

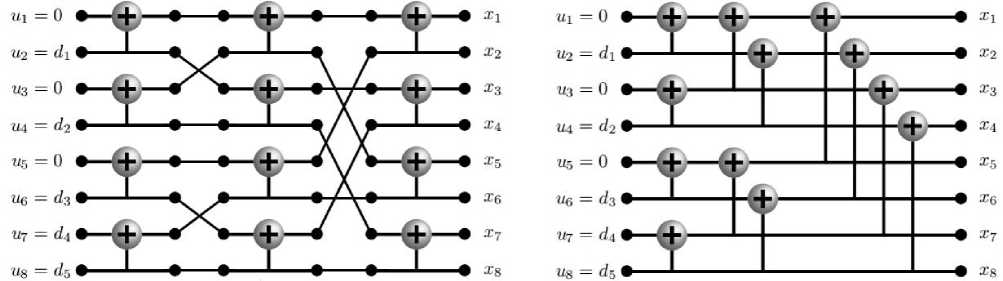
Рис. 1. Схемы полярного (8, 5, {1, 3, 5})-кода: bit-reversed ( а ); non-reversed ( б )

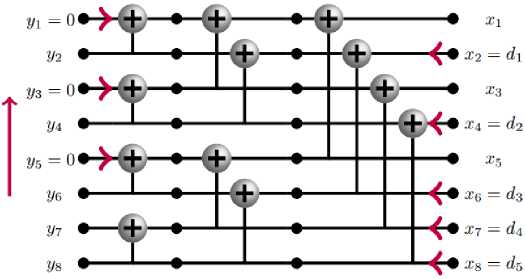
Рис. 2. Схема систематического non-reversed полярного кодирования (8, 5, {1, 3, 5})-кодом

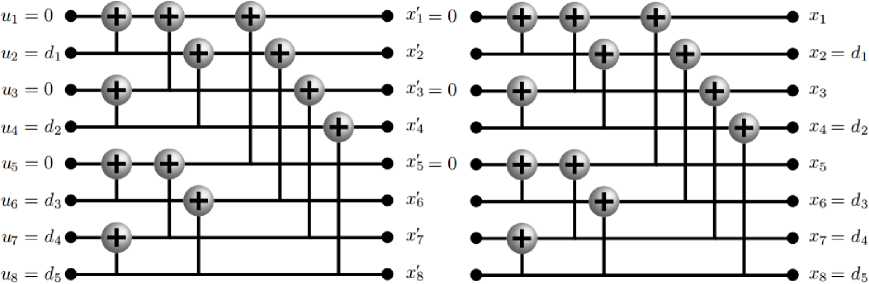
Рис. 3. Схема систематического кодирования на основе несистематического non-reversed кодирования (8, 5, {1, 3, 5})-полярным кодом

Прекодирование информации. Термином «прекодирование» обозначим операцию преобразования информационного сообщения d ₁ ^K в сообщение u ₁ ^N в соответствии с множеством A c :

f ( d i^K , A c ) = u N .

Прекодирование для (8, 5, {1, 3, 5})-кода будет выглядеть так:

f ({ d i , d 2 , d 3 , d 4 , d ₅ },{1,3,5}) = {0, d 1 ,0, d 2 ,0, d 3 , d 4 , d 5 }.

Введем понятие маски полярного кода. Маска полярного кода – это вектор m длины N такой, что m i = 0 для i e A c и m i = 1 для i t A c . Для (8, 5, {1, 3, 5})-кода маска полярного кода имеет вид m = {0, 1, 0, 1, 0, 1, 1, 1}.

Операция прекодирования может быть реализована с использованием регистров сдвига вправо (рис. 4, 5). Прекодирование (8, 5, {1, 3, 5})-полярного кода потребует 5-разрядный сдвиговый регистр D для вектора d , 8-разрядный сдвиговый регистр M для вектора m и 8-разрядный сдвиговый регистр U для вектора u .

Сдвиг в регистре M осуществляется на каждом цикле работы, на выход поступает значение младшего бита M 1. Сдвиг в регистре D осуществляется при условии M 1 = 1. Входной сигнал регистра U равен M 1 ^ D 1 . На рис. 4, а описывается состояние регистров прекодера (8, 5, {1, 3, 5})-полярного кода. В первый цикл работы осуществляется загрузка вектора m в регистр M и вектора d в регистр D . Непосредственно операция прекодирования осуществляется за следующие 8 циклов. Таким образом, прекодирование вектора u для (8, 5, {1, 3, 5})-кода осуществляется за N+ 1 циклов. Схема прекодера (8, 5, {1, 3, 5})-полярного кода приведена на рис. 5, а .

Перейдем к обобщенной схеме прекодера с разрядностью P регистров сдвига D , M и U , кратной N и K. Рассмотрим подробно диаграмму состояний такого прекодера с P = 4, представленную на рис. 4, б :

Цикл 1: загрузка d14 в рег. D; загрузка m4 = {1,1,0,1} в рег. M; простой в рег. U.

Цикл 2: сдвиг в рег. D ; сдвиг в рег. M ; U 4 = d 1 .

Цикл 3: сдвиг в рег. D ; сдвиг в рег. M ; U 3 ⁴ = { d 1 , d 2 }.

Цикл 4: простой в рег. D ; сдвиг в рег. M ; U 2 = { d 1 , d ₂,0}.

Цикл 5: сдвиг в рег. D ; сдвиг в рег. M ; U 1 ⁴ = { d 1 , d ₂,0, d 3 } - прекодирование u 4 завершено.

Цикл 6: простой в рег. D ; простой в рег. M ; простой в рег. U .

Цикл 7: простой в рег. D ; загрузка m 8 = {0,0,1,0} в рег. M ; простой в рег. U .

Цикл 8: простой в рег. D; сдвиг в рег.

U ⁴ = { d 2 ,0, d 3 ,0}.

Цикл 9: простой в рег. D; сдвиг в рег.

U 1 ⁴ = {0, d 3 ,0,0}.

Цикл 10: сдвиг в рег. D; сдвиг в рег.

u 1 ⁴ = { d 3 ,0,0, d 4 }.

Цикл 11: загрузка d ₅⁸ в рег. D ; простой в рег. M ; простой в рег. U .

Цикл 12: простой в рег. D ; сдвиг в рег. M ; U 1 ⁴ = {0,0, d 4 ,0} - прекодирование u 8 завершено.

Цикл 13: простой в рег. D ; загрузка m 92 = {1,1,0,1} в рег. M ; простой в рег. U .

Цикл 14: сдвиг в рег. D ; сдвиг в рег. M ;

U 1 ⁴ = {0, d ₄,0, d ₅}.

Прекодирование u14 длилось в течение циклов 1–5, начиная с загрузки d14 и m14 , затем в течение цикла 6

происходит простой прекодера. Прекодирование u58 длилось в течение циклов 7–12, начиная с загрузки m58 . Разница в один цикл связана с тем, что при пре- кодировании u58 загрузка m58 и d58 происходит в цик- лах 7 и 11 соответственно. Таким образом, простои, аналогичные простою в цикле 6, вводятся для того, чтобы прекодирование P бит всегда осуществлялось за P+2 цикла. Схема обобщенного прекодера с P = 4 представлена на рис. 5, б.

Для реализации необходимо добавить сигналы разрешения сдвига Shift_en для регистров M и U . Shift_en = 0 в том случае, если регистр маски M уже не содержит бит маски, но еще не прошло P +2 цикла с прошлой операции прекодирования.

Методы аппаратной реализации несистематического кодирования. Схемы несистематических полярных кодов, рассмотренные выше, могут быть реализованы в виде комбинационной схемы – параллельного кодера. Такое устройство имеет N входов, включает в себя N (log2 N) элементов «исключаю- щее ИЛИ» и осуществляет кодирование за n этапов.

Очевидным недостатком такого решения является его плохая масштабируемость, поскольку при параллельной реализации разрядность входа и выхода такой схемы равна длине кодового слова N. Для минимизации разрядности входа и выхода схемы кодирования необходимо применение методов конвейеризации вычислений [14].

Первым из рассматриваемых вариантов применения методов конвейеризации является конвейерная схема несистематического bit-reversed кодера [15; 16] с разрядностью входного и выходного сигнала P и длиной кодового слова N . На рис. 6. Представлена схема с P = 4 и N = 16.

Другой вариант – конвейерный несистематический non-reversed кодер с P = 4 и N = 16, представлен на рис. 7 [13]. В таблице приведены сравнительные характеристики параллельного кодера и рассматриваемых схем.

Как видно из таблицы, кодер 1 требует меньшего количества элементов «исключающее ИЛИ», чем кодер 2. Недостаток кодера 1 проявляется при реализации систематического кодирования согласно схеме на рис. 4. В этом случае требуется хранить маску полярного кода в non-reversed форме для осуществления прекодирования информации и в bit-reversed форме для наложения маски в ходе систематического кодирования, что влечет за собой дополнительные расхо- ды ресурсов памяти.

Цикл	D5	D4	D3	D2	Dl	Ms	M7	Мб	M5	M4	М3	М2	Ml	U8	U7	U6		U4	из	U2	Ul	Цикл	Di	Di	Di	Dl	Mi	Mi	M?	M1	Ui	Ui	U2	Ul
1. 2 з' 4 5 6 7* 8 9 ю’ 11 12 13 14 15 16 17 18 19	ds	di	ds	d2	di	1	1	1	0	1	0	1	0	0	0	0	0	0	0	0	0	1 2 3 4_ 5_ 6_ 7_ 8_ 9_ 10 11 12_ 13 14	di	di	d?	di	1	о	1	1	0	0	0	0
	d5	di	di	di	dl	0	1	1	1	0	1	0	1	0	0	0	0	0	0	0	0		0	d4	dl	ds	0	1	0	1	di	n	0	0
	0	di	di	di	di	0	0	1	1	1	0	1	0	dl	0	0	0	0	0	0	0		0	0	di	di	0	0	1	0	di	di	0	0
	0	di	d4	di	di	0	0	0	1	1	1	0	1	0	di	0	0	0	0	0	0
																							0	0	di	di	0	0	0	1	0	di	dl	0
	1	0	di	di	di	0	0	0	0	1	1	1	0	di	0	di	0	0	0	0	0
																							0	0	0	di	0	0	0	0	d3	0	dl	dl
	0	0	di	d4	di	0	0	0	0	0	1	1	1	0	di	0	dl	0	0	0	0
	0	0	0	ds	d4	0	0	0	0	0	0	1	1	d3	0	d:	0	di	0	0	0		0	0	0	di	0	0	0	0	di	0	di	di
	0	0	0	0	di	0	0	0	0	0	0	0	1	di	di	0	di	0	di	0	0		0	0	0	di	0	1	0	0	di	0	di	di
	0	0	0	0	0	0	0	0	0	0	0	0	0	ds	dJ	ds	0	dl	0	di	0		0	0	0	d4	0	0	1	0	0	di	0	dl
	di	d4	di	d2	di	1	1	1	0	1	0	1	0	d5 di	d4	di	0	di	0	di	0		0	0	0	d4	0	0	0	1	0	0	di	0
	d:	di	di	di	dl	0	1	1	1	0	1	0			di	di	di	0	d2	0	dl		0	Cl	0	0	0	0	о	0	di	0	n	di
	0	di	d4	di	dz	0	0	1	1	1	0	1	0			d5 0	d4	cb	0	di	0		ds	d7	de	ds	0	0	0	0	di	0	0	dl
	1	di	d4	di	di	0	0	0	1			0	]	0	di		ds ■	di	ds	0	di
																							ds	d7	de	ds	0	0	0	0	0	(14	0	0
	0	0	d5	d4	d3	0	0	0	0	1	1	1	0	d2	0	dl		di	d4	d3	0
																							ds	d7	de	ds	0	0	1	1	0	di	0	0
	0	0	di	di	di	0	0	0	0	0	1	1		0	di	0	dl		di 3	di	di
																							0	ds	d7	de	0	0	0	1	ds	0	di	0
	0	0	0	(1	d4	0	0	0	0	0	0	1		d3	0	d?	0	d!		ds 0	d4 d5
	1	0	0	0	di	0	0	0	1	0	0	0		di	di	0	di	0	di
	0	0	0	0	0	0	0	0	0	0	0	0	0	di	di	d3	0	di	0	dl	0
	di	d4	d3	d:	di	0	1	1	0	1	0	1	0	d?	d4	di	0	d2	0	dl 0
						а																б

Рис. 4. Состояние регистров прекодера (8, 5, {1, 3, 5})-полярного кода ( а ); состояние регистров обобщенного прекодера с P = 4 ( б )

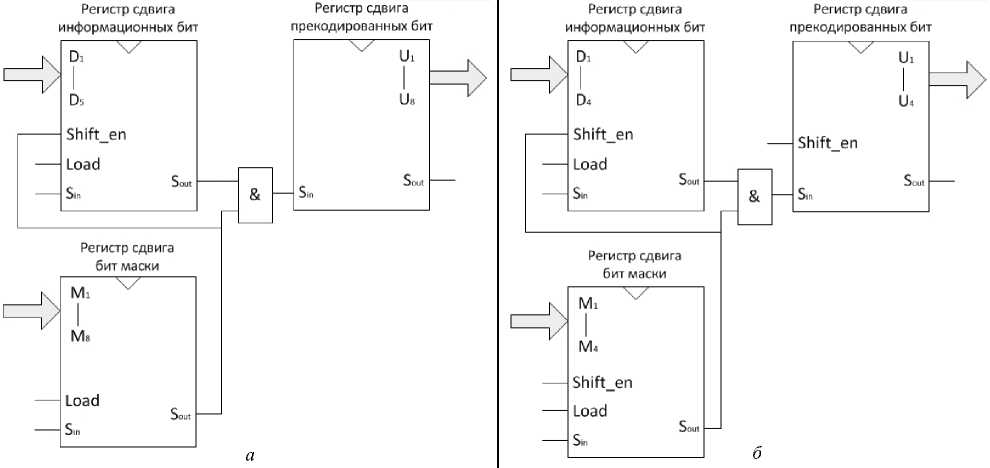
Рис. 5. Схема прекодера (8, 5, {1, 3, 5})-полярного кода ( а ); обобщенная схема прекодера ( б )

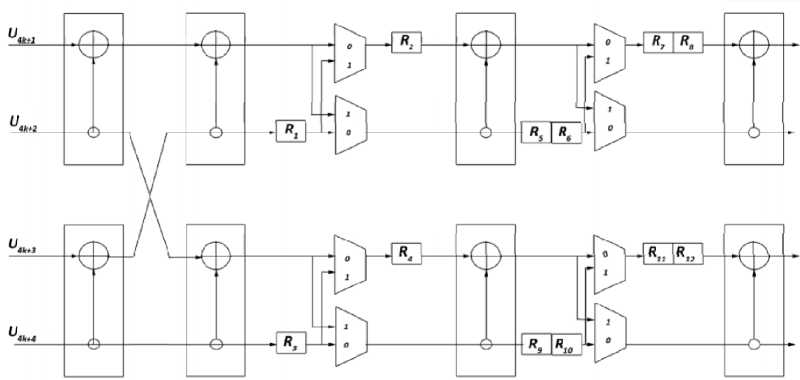
Рис. 6. Конвейерный несистематический bit-reversed (16, K )-кодер с P = 4 (кодер 1)

Сравнительные характеристики рассматриваемых схем кодирования

Характеристики	Параллельная схема	Кодер 1 [15; 16]	Кодер 2 [13]
Разрядность	N	P	P
«Искл. ИЛИ»	N ( log 2 N )	р ( log 2 N )	^P ^f lo^g 2 TP )
Регистры	–	P ^f N - 1) k P )	P ^f ^N — 1) k P )
Мультиплексоры	–	P f log₂ P )	p f iog₂ N )
Задержка кодирования	0	N + P - 2 P	N + P - 2 P

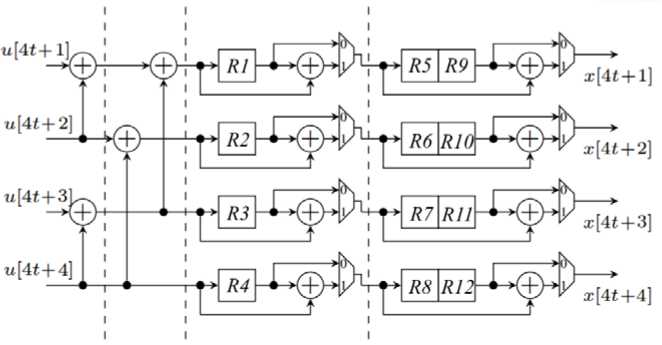
Рис. 7. Конвейерный несистематический non-reversed (16, K )-кодер с P = 4 (кодер 2)

Кодер систематического полярного кода. На рис. 8 представлена структурная схема разработанного устройства систематического (32, 16)-полярного кода с разрядностью P = 8. Систематическое кодирование реализуется в соответствии со схемой на рис. 3. Временная диаграмма конвейера систематического (32, 16)-кодера представлена на рис. 9.

Блок «Прекодер» реализует операцию прекодирования и является обобщенным прекодером с P = 8. Он преобразует информационное сообщение I в вектор U в соответствии с маской полярного кода M, результат записывается в регистр 1. Блоки «НСК 1» и «НСК 2» – конвейерные несистематические non-reversed (32, K)-кодеры с P = 8. Блок «НСК 1» кодирует вектор U в X’. Наложение маски M на вектор X’ осуществляется с помощью двухвходового элемента «И», результат записывается в регистр 2. Затем блок «НСК 2» кодирует преобразованный вектор X’ в вектор X, который и является кодовым словом.

Кодирование сообщения ( N , K )-кодером разрядности P осуществляется за ^N _P стадий, длительность „ f N Л .

каждой стадии составляет 21 — -11 + 3 цикла, общее время кодирования составляет 3 P циклов. Отноше- ние длительности цикла предлагаемого систематиче- ского кодера TСК к длительности цикла блока «Прекодер» ТПр описывается выражением TСК = (P + 2)ТПр.

Разработанный систематический кодер был смоделирован в пакете Altera Quartus II 13.0 с использованием системы ModelSim 10.1. На рис. 10 приведены результаты симуляции в системе ModelSim 10.1. Моделировалось систематическое кодирование информационного сообщения d = 16’ h {2 F , 59} (32, 16)-полярным кодом с маской m = 32’ h {88, E 8, E 8, EE }. Результат кодирования равен x = 32’ h { AC , AC , 53, 5 C }. Результат моделирования совпадает с результатом моделирования систематического полярного (32, 16)-кода в пакете MATLAB R2016b, построенного с использованием библиотеки [17].

Заключение. В работе представлен обзор метода помехоустойчивого кодирования, получившего название полярного кода. Рассмотрены методы кодирования полярными кодами и варианты их аппаратной реализации. Выделена операция прекодирования, предложен метод ее аппаратной реализации. Разработано устройство систематического кодирования полярными (32, K )-кодами, реализующее также и операцию прекодирования, проведено его моделирование. Разработанное устройство может быть масштабировано для кодирования информации полярными кодами с практически значимыми значениями длины кодового слова N .

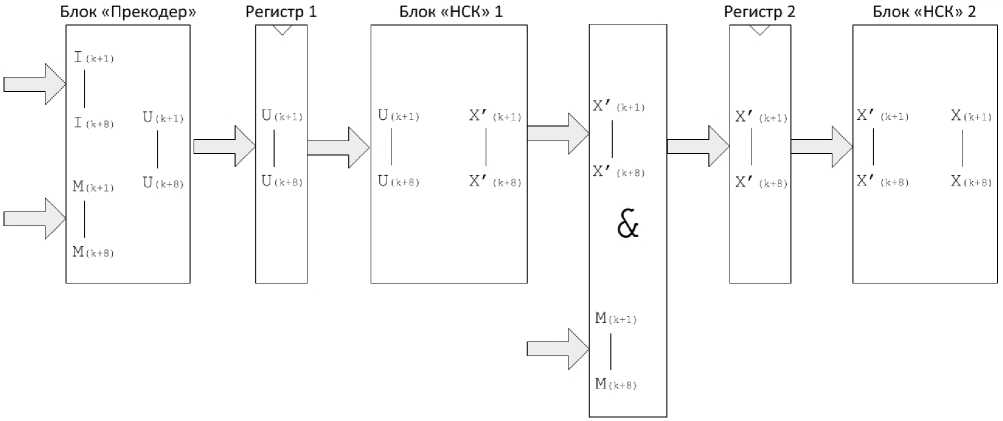
Рис. 8. Структурная схема систематического (32, 16)-кодера

12 3456789 10 11 12

Цикл

Прекод-е бит Ui-Ue

Загрузка бит Ui-Ui в Регистр 1

НСК 1 бит Ui-Us

Шаг 1

НСК 1 бит U1U» Шаг 2

НСК 1 бит Ui-Ui ШагЗ

Наложение Mi Мина X’l-X'a, запись ■ Регистр?

НСК 2 бит X'1-X'i Шаг1

НСК 2 бит X'1-X'i

Шаг 2

НСК 2 бит X'i-X'« ШагЗ

Прекоде бит U«-Uu

Загрузка бит U>Uib r Регистр 1

НСК1 бит Uv-Uib

Шаг 1

НСК1 бит Ui-Uib

Шаг 2

НСК1 бит U»-Uib ШагЗ

Наложение

Mv-Mib на х>Х*и, запись ■ Регистр 2

НСК 2 бит Uv-Uib

Шаг 1

НСК 2 бит Х'а-Х'ть

Шаг 2

НСК 2 бит Х'е-Х'ть ШагЗ

Прекод-е бит U17-U24

Загрузка бит U17-U* в Регистр 1

НСК1 бит Uv-Um Шаг 1

НСК1 бит Uv-Um Шаг 2

НСК1 бит Uit-Um ШагЗ

Наложение Mi»-M.'« на х*|>-х'м, запись ■ Регистр 2

НСК 2 бит Х'п-Х'м Шаг 1

НСК 2 бит X'lz-X'ia

Шаг 2

НСК 2

бит Х'12-Х'м ШагЗ

Прекод-е бит UjvUu

Загрузка бит Um-Uu в Регистр 1

НСК1 бит UivUu Шаг 1

НСК1 бит Um-Uu Шаг 2

НСК1 бит Uk-Uu ШагЗ

Наложение

М2уМп на

Кп*м, МЛиО.

• Регистр 1

НСК 2 бит Х'и-Х'м Шаг 1

НСК 2 бит Х'п-Х'и Шаг 2

НСК 2 бит X'ivX'u ШагЗ

¹' Блок кода

Рис. 9. Временная диаграмма конвейера систематического (32, 16)-кодера

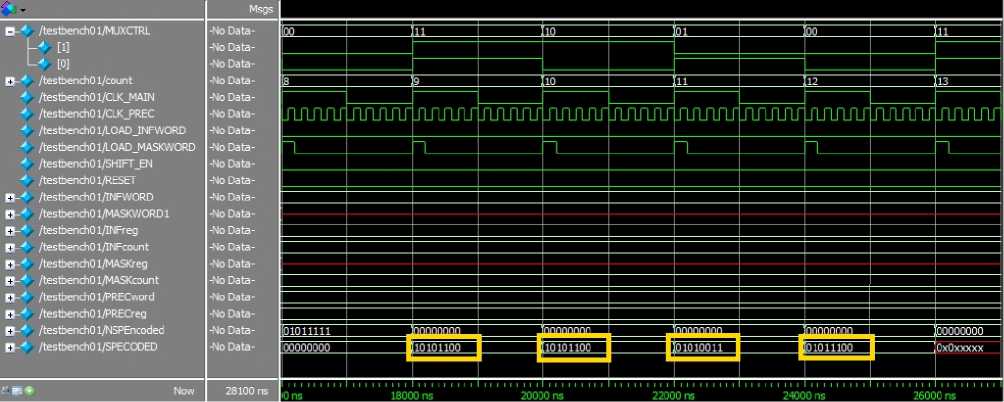
Рис. 10. Результаты симуляции в системе ModelSim 10.1

Список литературы Аппаратная реализация кодирования информации систематическими полярными кодами

Arikan E. Channel polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels. IEEE Transactions on Information Theory. 2009, Vol. 55, No. 7, P. 3051-3073 DOI: 10.1109/TIT.2009.2021379
Eslami A., Pishro-Nik H. On bit error rate performance of polar codes in finite regime. IEEE Communication, Control and Computing 48th Annual Allerton Conference. 2010, P. 188-194. Doi: 10.1109/ALLERTON.2010.5706906.
Leroux C., Raymond A. J., Sarkis G. A semi-parallel successive-cancellation decoder for polar codes. IEEE Transactions on Signal Processing. Vol. 61, No. 2, 2013. P. 289-299 DOI: 10.1109/TSP.2012.2223693
Arikan E. Systematic polar coding. IEEE Communications Letters. 2011, Vol. 15, No. 8, P. 860-862.
Tal I., Vardy A. List decoding of polar codes. IEEE International Symposium on Information Theory. 2011, P. 1-5.
Niu K., Chen K. Stack Decoding of Polar Codes. Election Letter. 2012, Vol. 48, No. 12, P. 695-696 DOI: 10.1049/el.2012.1459
Trifonov P., Miloslavskaya V. Polar subcodes. IEEE Journal on Selected Areas in Communications. 2016, Vol. 34, No. 2, P. 254-266. 2504269 DOI: 10.1109/JSAC.2015
Leroux C., Raymond A. J. Hardware Implementation of Successive Cancellation Decoders for Polar Codes. Journal of Signal Processing Systems archive. 2012, Vol. 69, No. 3, P. 305-315 DOI: 10.1007/s11265-012-0685-3
Leroux C., Tal I. Hardware architectures for successive cancellation decoding of polar codes. IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2011. 5946819 DOI: 10.1109/ICASSP.2011
Vangala H., Viterbo E., Hong Yi. A Comparative Study of Polar Code Constructions for the AWGN Channel. Available at: https://arxiv.org/abs/1501.02473? context=cs (accessed: 28.11.2016).
Vangala H., Viterbo E., Hong Yi. Efficient systematic polar encoding. IEEE Communication Letters. 2016, Vol. 20, No. 1, P. 17-20. 2497220 DOI: 10.1109/LCOMM.2015
Sarkis G., Giard P., Vardy A., Thibeault C., Gross W. J. Fast Polar Decoders: Algorithm and Implementation. IEEE Journal on Selected Areas in Communications. 2014, Vol. 32, No. 5, P. 946-957 DOI: 10.1109/JSAC.2014.140514
Sarkis G., Tal I. Flexible and Low-Complexity Encoding and Decoding of Systematic Polar Codes. IEEE Transactions on Communications, 2015. Doi: 10.1109/TCOMM.2016.2574996.
Parhi K. K. VLSI Digital Signal Processing Systems: Design and Implementation. USA, Wiley, 1999, 784 p.
Indumathi G., Aarthi Alias Ananthakirupa V. P. M. B., Ramesh M. Architectural Design of 32 Bit Polar Encoder. Circuits and Systems. 2016, No. 7, P. 551-561 DOI: 10.4236/cs.2016.75047
Yamuna devi S., Magdalinjoenita G., Revathi V. An Advanced Architecture for 16-bit Polar Codes using Partially Parallel Encoder. International Journal of Advanced Research in Electronics and Communication Engineering (IJARECE). 2016, Vol. 5, No. 1, P. 16-18.
Vangala H., Viterbo E., Hong Yi. Polar coding algorithms in MATLAB. Available at: https://ecse. monash.edu//staff/eviterbo/polarcodes.html (accessed: 24.11.2016).

Еще

Статья научная