Application of bird swarm algorithm for allocation of distributed generation in an Indian practical distribution network

Published Online July 2019 in MECS

Electric distribution network represents the final electrical connection between the power consumers and huge power supply system. The distribution network is a complex system and having about 70% of the total loss owing to the high value of R/X. Minimization of such high loss is a perplexing task for distribution firms. The major techniques of power loss minimization are capacitor placement, network re-configuration and DG placement [1]. From the past few years, DG placement is becoming a renowned area of research. Several types of DGs and their definitions have been discussed in [2]. DG is a lesser quantity power production that is directly fed to the load/distribution side rather than the transmission system [3]. It is also named as “dispersed generation”, “decentralized generation” or “embedded generation” [4]. DG is mainly classified [5] into two categories based on the type of fuel consumed renewable energy resource based DGs and non-renewable energy resource based DGs. A few years back, DG is modeled as an active power source only but now with advances in technology DGs exists in different kinds [6] such as:

Type-1 DG: generates active power only. For example photovoltaic, microturbines

Type-2 DG:  generates reactive power. For instance synchronous condenser, capacitor

Type-3 DG: generates active and reactive power. The synchronous generator is the best example for it

Type-4 DG: injects real power and consumes reactive power. The induction generator is an example of it

Incorporation of DG into the distribution network (DN) facilitates several advantages [7] such as curtailed power loss, voltage magnitude enrichment and reduced financial investment on the expansion of the existing network and reduced emission. DG location significantly affects the performance of DN. Incorrect placement of DG may cause increased loss, operation and investment cost [8]. However, the appropriate DG placement helps in maximizing the technical, financial and environmental benefits from the DG.

The remaining sections of this paper are arranged as follows: Section II explains related work. Section III presents problem formulation and system constraints. Section IV and V discuss proposed CSI and BSA methods. Finally, sections VI and VII present experimental results and final conclusions, respectively.

• II.    Related Work

There are numerous analytical and optimization methods utilized in the literature. A 2/3 analytical method has been used in [9] by considering network loss minimization as an objective. According to this rule in a balanced DN, power loss minimization will be more, if the DG is placed at a distance of 2/3 from the feeder with a 2/3 size of DG. The main defect in this method is, it is suitable only for a balanced distribution system but not suitable for the unbalanced system. An analytical method was proposed by authors in [10] for optimal allocation (sizing and sitting) of time-varying DGs in radial as well as networked DNs with time-varying loads. An analytical method for minimization of power loss in DN by optimal placement and sizing using power stability index was proposed by authors in [11]. Simultaneous allocation of DG and the capacitor was proposed [12]. In [12] Sensitivity analysis is employed for optimal placement and analytical method is used for sizing.

Authors in [13] suggested a particle swarm optimization, artificial bee colony optimization [14] techniques for network loss reduction using optimal DG sitting. In [15], SOS (symbiotic organisms search) algorithm, Stud krill herd algorithm [16], grey wolf optimization [17] were employed for multi-DG allocation in radial DNs. Multiple DG placements under different load models using invasive weed optimization algorithm was proposed [18].

In this paper, a novel combined sensitivity index (CSI) based on both magnitude of load apparent power and voltage sensitivity is used to identify the optimal nodes for DG integration. However, the optimal DG size is calculated using a new population based BSA. Here, an objective function is modeled to minimize the network power loss.

I V m + 1 | 2 “ I V m | 2 ^{— 2(} R m , m + 1 ^X P m ⁺ X m , m + 1 ^X Q m )-

22   mm

... ⁺ ( R m , m + 1 ⁺ X m , m + 1 ) ^X .     _l2

^{,               ,}              | V m |²

C. DG Penetration Level

It is represented as given in (5)

DG pl =

KVA DGp x 1oo KVA Load

D. Voltage Deviation

Voltage deviation is calculated using (6).

Deviation

■^ I V rated - V j\

^

j = 1        rated

E. Voltage Limit

The magnitude of voltages of all buses should lie within the pre-specified range and is represented as^

min          max

V j ^- V j ^- V j

Here, V™ = 0.9 pu and Vj^max = 1.1 pu

• III.    P roblem F ormulation and C onstraints

• A.    Mathematical Problem Formulation

To gain the considerable benefits from the DG, DG must be positioned at the appropriate bus/node with a suitable size. The main motive of this problem is to diminish the network loss. The sum of total network loss is considered as fitness function and is calculated as

P otalloss = min ^J'  ( j , j + 1)          (1)

j = 0

Where, nb=total number of nodes and

P _loss (j, j + 1) =Real loss between j^h node and (j+1)^h node

• B.    Power Flow Constraints

Real power (2) and reactive power (3) flow in each branch and end bus voltage (4) is determined as follows

P m + 1 = P m + P DG

—

22 mm

P L , m + 1    R m , m + 1      .     .2

| V_m |

Q m + 1 = Q m + Q DG — Q l , m + 1

—

22 mm ^m , ^{m + 1}      I у |2

| V_m |

• IV. P roposed CSI

Optimal location of DG plays a vital role in voltage profile enhancement. Most researchers have used voltage sensitivity analysis and artificial intelligent techniques in the past to identify optimal locations for placement DG units. Many researchers and scientists have suggested sensitivity techniques based on power loss, voltage and a combination of both to solve optimal DG placement problem. In this work, proposed CSI [19] is employed to locate the most suitable nodes/buses to incorporate the DG units on an Indian practical 52-bus RDN. It mainly depends on

• •    Voltage sensitivity

• •   Apparent power of a connected load (KVA)

CSI (Sb) is mathematically modeled as follows nb

S b = E ^V k , b * ^KVA k +^A Vb™^          (8)

k = 2

For K =2, 3, 4,…… nb

Note that bus ‘1’ is a reference bus or substation bus and nb is the maximum number of nodes in the system.

The maximum change in voltage magnitude ( A V_b max ) after the placement of DG unit is represented as follows:

max             act    base

A V b   = ma^x| V k, b - V k, ь  |

Here, variables V _k ^a _b ^ct and V _k ^b _b ^ase are voltages at node ‘ b’ after and before placement of DG at node ‘k’, respectively.

The KVA magnitude of connected load at bus ‘ k ’ is calculated as follows:

KVA k =   ( PL . ) 2 + ( QL k ) 2          (10)

Here, PL and QL are active power magnitude and reactive power magnitude of connected load at node ‘ k’ .

Importance of first term of (8) is that the buses with higher KVA loads should keep those node voltages at higher values as possible. Second term is the maximum voltage magnitude change due to DG placement. Ranking of buses in each feeder is obtained using (8). The value of S_b is calculated at each bus (except reference bus) by injecting active power of 10%, 20% and 30% of total active power. Bus with highest S b value should be selected as candidate bus to place DG unit. Top five sensitive buses in each feeder of an Indian practical 52-bus RDN are given in Table 1. As nodes 19, 24 and 50 are being on top in the priority list, they are selected as candidate nodes to place DG units.

Table 1. Ranking of buses

Rank of buses	Feeder 1			Feeder 2			Feeder 3
	DG power injection (% of TRPL)			DG power injection (% of TRPL)			DG power injection (% of TRPL)
	10	20	30	10	20	30	10	20	30
1	19	19	19	24	24	24	50	50	50
2	18	18	18	26	26	26	52	52	52
3	17	17	17	23	23	23	51	51	51
4	15	15	15	31	31	31	49	49	49
5	14	14	14	25	25	25	48	44	48

• V. B ird S warm A lgorithm

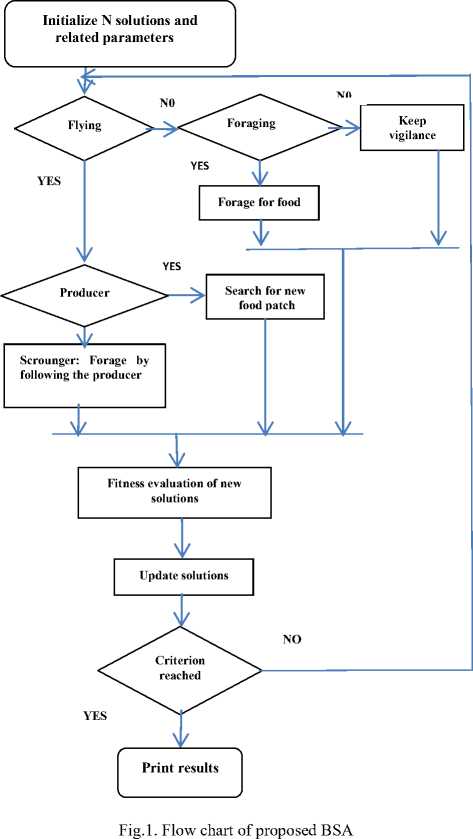
  In this problem, Bird swarm algorithm (BSA) is used to determine the size/capacity of DG units. BSA [20] is a very recently (2015) developed, bio-inspired optimization technique. BSA is developed based on the intelligence observed in communication and social behavior of bird swarms. Basically, most of the birds exhibit three types of behaviors such as foraging, vigilance and flight behavior.

• A.    Foraging Behavior

All birds in the swarm quests for food based on its previous knowledge and swarms experience. These actions can be mathematically expressed as below:

X m + П = X t,. , n + (P m , n - < , n ) X C X rand(0,1)

.... + (g n - X tn , n ) X ⁵ X rand (0,1)                 ⁽¹¹⁾

In the above expression (11) rand(0,1) represents a randomly generated number between (0,1) and n e [1,2,.... D ]. 5 and C are respectively named as social accelerated and cognitive accelerated coefficients and both are positive numbers. P m,n is the previous best position of m ^th bird and g is the previous best position of a swarm.^

• B.    Vigilance Behavior

Each and every bird in the swarm tries and competes with the rest of the swarm to get a position in the middle of the swarm to safeguard themselves from the predators. Hence, each bird in the swarm would not move continuously towards the center. The mathematical representation of these motions is as follows:^

X m + n = X m , n + A ¹⁽ mean n - X m , n ) ^x rand (0л

.... + A2(Pq,n -xm,n) X rand(-1,1)

( PFit)

A1 = a1X exp I--x N I

I sumFit + e(

A 2 = a 2 x exp

(  PFitm - PFita mq j | PFitq - PFitm \+e

N x PFit_a ) q_ sumFit + e 7

Where, q ( q * m ) is a randomly selected positive number between 1 and N. a1 and a2 are positive numbers in [0 2]. PFitm represents the mth bird’s best fitness value. sumFit denotes sum of the best fitness of all the birds in the swarm. e is a small number to eliminate zero-division error and meann represents nth bird average position.

• C.    Flight Behavior

While searching food the birds may travel from one location to other location due to predation threat or any other reason and once again at the arrived site they would forage for food. Some birds of the swarm called producers would quest for food patches while the rest of the swarm called scroungers try to forage the food patches identified by the producers. The mathematical representation of producer and scrounger behavior may be as follows:

X m'л = X m , n + randn (0,1) ^x X m , n          (15)

X m + n = X m , n + ( X‘ q , n - X m , n ) ^x FL ^x rand (0,1)   (16)

Here, randn(0,1) represents Gaussian distributed random value with 0 and 1, respectively as mean and standard deviation and FL represents the following factor. The flow chart of the proposed BSA is shown in Fig.1.^

STEP: 5 Find out the test system power loss for generated DG sizes

STEP: 6 Sort out DG size with lowest power loss

STEP: 7 Update DG sizes using expressions (11)-(16)

STEP: 8 Find out power loss for updated DG sizes

STEP: 9 Update current best DG size if the power loss obtained in step 8 is less than power loss obtained in step 5 otherwise moves to step 7.

STEP: 10 Stop if the criterion is satisfied

• C. Implementation of BSA

The complete algorithm of the proposed method is as follows:

STEP: 1 Load test system line and load data to run power flow program.

STEP: 2 Find the most suitable bus in each feeder using the expression (8) to place DG

STEP: 3 Initialize population and other BSA parameters.

STEP: 4 Generate birds (DG sizes) using (17)

DGsize = ( DG max - DG ^i^ )*rand () + DG ^in   (17)

• VI.    Experimental Results

  In this article, minimization of network loss is taken as an objective and is reached by incorporating multiple DG units into the network. The suitable DG location and size are found out by CSI and BSA. The complete optimization program has been implemented and executed on MATLAB R2014a version installed in Intel Core i3, 4GB RAM HP laptop. Control parameters employed in the execution of proposed BSA are presented in Table 2 and are same for all cases.

Table 2. Control parameters of BSA

Parameter	Value
Number of birds	30
Maximum iterations	100
Cognitive accelerated coefficient	1
Social accelerated coefficient	1
Constants (a1 and a2)	1.5

Table 3. Specifications of Indian practical 52-bus RDN

Base KVA	Base KV	Connected load		Power loss
		KW	KVAr	KW	KVAr
1000	11	4184	2025	887.19	381.69

The BSA is being applied to 52-bus Indian practical RDN [21]. The detailed specifications of this test system which is portrayed in Fig. 2 [22] are given in Table 3 and Appendix A. This test RDN is an arrangement of three feeders consists of total 52 nodes and 51 branches. The uncompensated/base case system is experiencing a total network loss of (887.19+j381.69) KVA. By applying CSI approach bus 19, 24 and 50 are selected as candidate buses to incorporate three DG units. In this work, the following cases are analyzed.

Case 1: Three DG units injecting active power at unity power factor (P.F)

Case 2: Three DG units injecting active and reactive power at 0.9 P.F

Case 3: Three DG units injecting active and reactive power at 0.95 P.F

According to the ranks of nodes, top three nodes i.e. nodes 19, 24 and 50 are selected to place DG units. The numerical results of case 1,2 and 3 are tabulated in Table 4 in terms of optimal DG position, size, and penetration level, loss reduction, minimum voltage level and voltage deviations.

Table 4. Results of Indian practical 52-bus RDN

particulars	Base case	Case-1	Case-2	Case-3
Σ KW loss	887.194	295.879	203.569	195.099
Σ KVAr loss	381.699	127.297	87.582	83.938
DG size and location (KVA)	0	696.95(19)	775.175(19)	780.859
		500.00(24)	500.00(24)	500
		1058.68(50)	1170..877(50)	1193.656
ΣDG penetration (%)	0	48.526	52.622	53.235
Best power loss		295.879	203.569	195.099
Average power loss		295.927	203.664	195.213
Worst power loss		296.052	204.080	195.608
Standard deviation		0.06134	0.0348	0.0330
|Vmin| (p.u)	0.6844	0.8923	0.9139	0.9166
Σ|Vdevi|	8.5796	3.0545	2.0850	1.9976

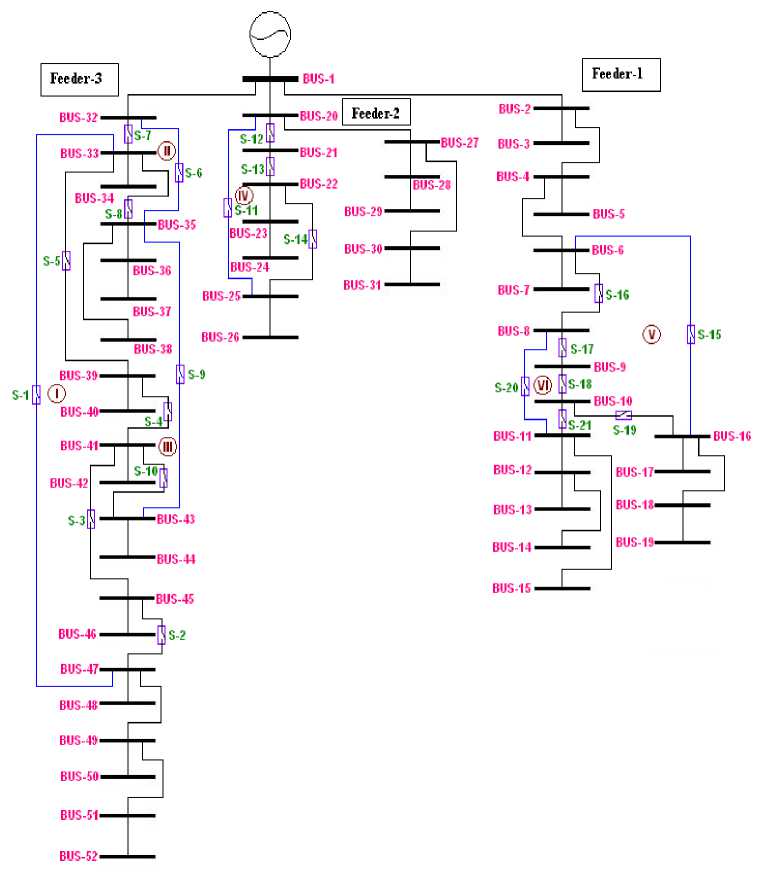
Fig.2. Single line diagram of Indian practical 52-bus RDN

In case 1, three DG units (Solar photovoltaic based) operating at unity P.F are placed at buses 19, 24 and 50. In this case, the active/real loss (ΣKW loss) is condensed from 887.194 KW to 295.879 KW (from table 4) and the minimum voltage (|Vmin|) level is improved to 0.8923p.u from 0.6844p.u. However, the total voltage deviation (Σ|Vdevi|) is reduced from 8.5796 to 3.0545. Three synchronous generator based DG units, supplying real and reactive power at 0.95 power factor are placed in case 2. With case 2, the real loss is abridged to 203.56 KW which is the smallest value as compared to case 1. The minimum voltage level and total voltage deviation, respectively, in this case, are 0.9139p.u and 2.085 that values are better than case.2. Now in case 3, synchronous generator based DG units injecting real and reactive power at 0.9 P.F are used. In this case injection of reactive power is increased as compared to case 2 which in turn results in more loss reduction with 195.09 KW. The minimum voltage (|Vmin|) level is improved to 0.9166p.u from 0.6844p.u. However, the total voltage deviation (Σ|Vdevi|) is reduced from 8.5796 to 1.9976.

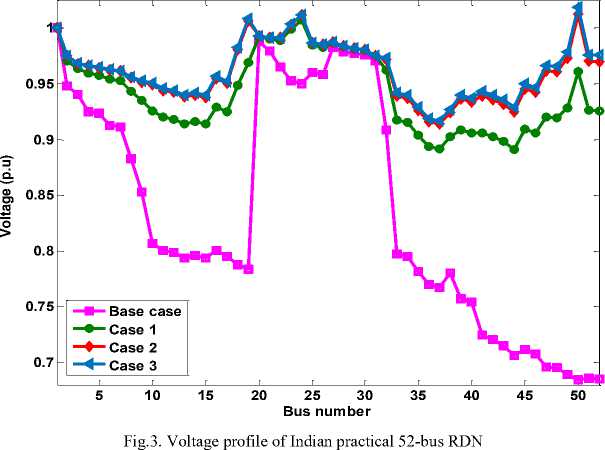
Maintaining all nodes of the distribution system within the specified voltage limit is one of the major concerns in electrical power systems. The voltage profiles of an Indian practical 52-bus distribution system before and after DG placement are portrayed in Fig. 3. Before installation of DG units (Base case), the minimum voltage in test system is 0.6844p.u (At node 50) and 32 nodes are not operating within the specified voltage limit.. However, with case 1, case 2 and case 3, the minimum voltage is improved to 0.8923p.u, 0.9139p.u and 0.9166p.u, respectively. With case 1, the nodes operating within the specified voltage limit are increased from 20 to 48. With case 2 and case 3, all nodes of the test system are brought within the specified voltage limit. However, total voltage deviation reduction is more in case 3 as compared to case 2.

• VII.    Conclusions

In this article, problem on optimal allocation of multi – distributed generation in an Indian practical 52-bus RDN has been solved. To minimize the search space in solving a problem, a novel sensitivity index called CSI has been used to identify the optimal nodes to place DG units. A nature inspired algorithm, Bird Swarm Algorithm, has been used to determine the optimal DG size. Two types of DG technologies (solar and biomass) operating at different power factors (1, 0.95, 0.9) are considered for power loss minimization and voltage profile enhancement. From the above obtained results, the following worth notes could be drawn.^

• •    By installing three type-1 (Solar) DG units at

64.39%.

nodes 19, 24 and 50, the active power loss is reduced by 66.65% and total voltage deviation by

• •    By installing three type-2 (Biomass) DG units operating at 0.95 P.F, the active power loss and total voltage deviation are reduced by 75.69% and 75.69%, respectively.

• •    By installing three type-2 (Biomass) DG units operating at 0.9 P.F, the active power loss and total voltage deviation are reduced by 78% and 76.71%, respectively.

• •    In case 1, case 2 and case 3, the minimum voltage level is improved from 0.6844p.u to 0.8923p.u, 0.9139p.u and 0.9166p.u, respectively

• •    From the above points, it is clear that as compared to other cases case-3 has been performed better in minimizing power loss and improving voltage profile.

37

35

38

0.0172

0.00740

68

33

38

33

39

0.0215

0.00925

95

46

39

39

40

0.0172

0.00740

108

52

40

39

41

0.0215

0.00925

41

20

41

41

42

0.0258

0.01110

95

46

42

41

43

0.0387

0.01665

27

13

43

43

44

0.0430

0.01850

122

59

44

41

45

0.0129

0.00555

108

52

45

45

46

0.0301

0.01295

81

39

46

45

47

0.0215

0.00925

68

33

47

47

48

0.0129

0.00555

41

20

48

47

49

0.0129

0.00555

68

33

49

49

50

0.0344

0.01480

81

39

50

49

51

0.0129

0.00555

108

52

51

51

52

0.0086

0.00370

41

20

Abbreviations and Acronyms

P totalloss	Total real power loss	KVA DG	Apparent power of DG
P m	Real power flow from mth bus	KVA Load	Apparent power of load
PL k	Active power at node K	QL k	Reactive load at node K
P m+1	Real power flow from (m+1)th bus	V m	Voltage of mth bus
P DG	Real power of DG	V m+1	Voltage of (m+1)th bus
P L,m+1	Real load of (m+1)th bus	V rated	Rated voltage
Q m	Reactive load of mth bus	V j	Voltage at bus j
Q m+1	Reactive load of (m+1)th bus	min	Minimum voltage at bus j
Q DG	Reactive power of DG	max	Maximum voltage at bus j
Q L,m+1	Reactive load of (m+1)th bus	X m,m+1	Reactance of branch between m and (m+1) bus
R m,m+1	Resistance of branch between m and (m+1) bus	X(j)	Reactance of branch j
R(j)	Resistance of branch j	nb	Number of buses

Appendix A

Line and load data of an Indian practical 52-bus radial distribution network.

S. No.	From bus	To bus	R (p.u)	X (p.u)	P (KW)	Q (KVAr)
1	1	2	0.0258	0.01110	81	39
2	2	3	0.0430	0.01850	135	65
3	2	4	0.0129	0.00555	108	52
4	4	5	0.0129	0.00555	108	52
5	4	6	0.0086	0.00370	27	13
6	6	7	0.0172	0.00740	54	26
7	6	8	0.0215	0.00925	135	65
8	8	9	0.0258	0.01110	81	39
9	9	10	0.0430	0.01850	67	32
10	10	11	0.0129	0.00555	27	13
11	11	12	0.0086	0.00370	27	13
12	11	13	0.0430	0.01850	108	52
13	12	14	0.0301	0.01295	54	26
14	12	15	0.0344	0.01480	94	45
15	10	16	0.0129	0.00555	67	33
16	16	17	0.0516	0.02220	67	33
17	16	18	0.0430	0.01850	108	52
18	18	19	0.0344	0.01480	81	39
19	1	20	0.0086	0.00370	108	52
20	20	21	0.0129	0.00555	94	46
21	21	22	0.0258	0.01110	81	39
22	22	23	0.0430	0.01850	108	52
23	23	24	0.0215	0.00925	108	52
24	22	25	0.0258	0.01110	102	50
25	25	26	0.0344	0.01480	41	20
26	20	27	0.0086	0.00370	108	52
27	27	28	0.0129	0.00555	162	79
28	28	29	0.0215	0.00925	68	33
29	27	30	0.0344	0.01480	68	33
30	30	31	0.0430	0.01850	95	46
31	1	32	0.0344	0.01480	41	20
32	32	33	0.0430	0.01850	121	59
33	33	34	0.0344	0.01480	41	20
34	33	35	0.0301	0.01295	41	20
35	35	36	0.0344	0.01480	135	66
36	36	37	0.0215	0.00925	81	40