Application of finite automata with genetic algorithms in JavaScript for determination of manpower system control
Автор: Kraba A., Kofja D., Nidari A., Rozman ., Maleti M.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Математика, механика, информатика
Статья в выпуске: 1 т.16, 2015 года.
Бесплатный доступ
The strict hierarchical manpower system is modeled in the state space where the desired number of men in particular rank is determined by predefined trajectory function. The transition model is represented by the principles of System Dynamics where each rank is represented as the state element and transition as the flow. The basis for the model is the structure of the exponential delay chain with additional outflows from particular states. The strategy for achieving the desired states is determined by the application of the genetic algorithms which are implemented in JavaScript as well as the System Dynamics model. Parameter boundaries were taken into consideration which was determined according to the historical data. Predetermination of the desired system states by the set of exponential functions reduced the optimization burden. The optimization problem was defined as the minimization of the sum of quadratic difference between desired and actual states in all ranks for the observed time horizon. Time boundaries in considered optimization problem were not constant which contributes to the complexity of the addressed optimization task. The six state finite automaton code realization is described which prevents the oscillations in the strategies. The algorithm for integration of system dynamics model and genetic algorithm with finite automaton is described.
Manpower system, finite automata, genetic algorithm
Короткий адрес: https://sciup.org/148177387
IDR: 148177387 | УДК: 519.234
Текст научной статьи Application of finite automata with genetic algorithms in JavaScript for determination of manpower system control
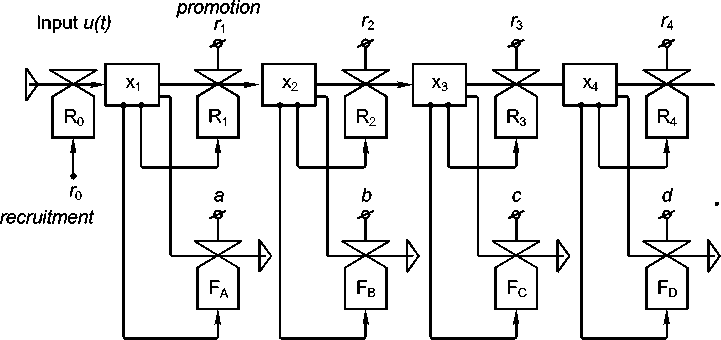
Introduction. Controlling of hierarchical manpower system such as military is demanding task [1–6] since the control problem includes several stochastic variables which should be considered, such as time variant boundaries on recruitment, promotions, retirements and wastages. The paper describes the methodology which was developed for the Slovenian Army restructuring [1; 7] where the new numbers of officers in the highest eight ranks should be determined. Due to the new standards, the new ratio should be established between the number of officers and number of soldiers. The structure of the system is shown in fig. 1. The system is modelled as the cascading exponential delay with the outflows as the wastages, i. e. fluctuations from the army. The input u ( t ) to the system represents recruitment which influences the inflow R 0 to the first element x 1 which represents the level of the first rank ( x 1 ) members (lowest rank). According to the promotion factor r 1 the transitions from rank x 1 to rank x 2 are made. The fluctuations from the rank x 1 are determined by the number of the x 1 rank members and the fluctuation factor a . Outflow element F A represents the wastage, i. e. the case where the member of the rank leaves the army. This structure is repeated arbitrarily however in our case eight ranks were considered. The system also does not allow for direct input to the particular rank x ; the way to the higher ranks is only possible to the recruitment to the first rank, x 1 therefore the system is strict hierarchical. In order to define the dynamics of the system the discrete state space is applied in the form x ( k + 1) = Ax ( k ) + Bu ( k ) [1]. State vector x represents the number of men in particular rank whereas matrix of coefficients A represents promotion factors r and wastage factors f . The only input to the system is recruitment represented by the Bu ( k ) term in the discrete state space.
In order to restructure the army manpower system, the recruitments, promotions, wastages and retirement should be determined in such a way, that new, desired numbers of man in particular rank x are achieved in minimal time. The solutions should not exercise the oscillations since this would lead to the undesired adaptation of training facilities and number of instructors. Another limitation that should be considered, is that the number of recruitments, promotions, wastages and retirement should not deviate significantly from the average numbers in previous 10 years. The novelty of the approach is twofold, on one side, the manpower system is modelled by the System Dynamics methodology, which is easy to understand, on the other side, the model is integrated with the Finite Automata in order to avoid the undesired oscillations in the strategy. Besides, we have developed technical realization of the system in JavaScript which provides new opportunities to apply the developed algorithm in the cloud as well as in the embedded devices [8].
Methodology description. For each rank x, the desired number of man is stated by the Human Resource department in the Slovenian army. This were only the final numbers of men that should be achieved in particular ranks x. Since the system is described by the model of exponential delay chain, it is anticipated, that the transitions will follow exponential functions. By anticipating the system response, the optimization burden could be reduced by the predetermination of the trajectories for states x. The response of the system will be exercised as the exponential approach to the goal values. By the determination of the desired response function one can reduce the optimization search space [9; 10]. In our case we defined the desired response by the function, describing the way in which the number of men in particular rank x should be reached. The following function has been defined:
f ( k ) = x, + ( x 0 - x )( k i - k ) e - pk , (1)
ki where x0 , x represent initial and final value of the state variable x, k is terminal time; k is simulation time and p e [0, от] is importance factor which determines the rate by which the goal is reached. The optimization problem where we want to achieve the desired values, marked with z in the equation (2) considers the minimal distance to the desired values function defined by equation (1):
tq min J = У (z(k) - x(k)) T G(z(k) - x(k))(2)
u,r, f subject to uLB (k) < u(k) < uUB (k), rLB(k) ^ r(k) ^ rUB(k), flb (k) < f (k) < fub (k), where G is time-invariant diagonal matrix of weights reflecting the importance of holding deviations for rank n as small as possible; z(k) represents the goal trajectory of the system defined by equation (1); tq is terminal time; uLB(k) and uUB (k) vectors of lower and upper boundary for recruitment in rank x1 , respectively; rLB(k) and rUB (k) vectors of lower and upper boundary for transitions r between ranks x, respectively (as well as output of the system from the last rank xn ); and fLB (k) and fUB (k) vectors of lower and upper boundary for fluctuations, i. e. wastages from rank x , respectively. Note that all boundaries are time dependent, which increases the complexity of the addressed optimization problem.
Described optimization problem should be augmented by the rule, that the gained strategy should not exercise undesired oscillations [1]. If, for example, the recruitment would oscillate e. g. between 0 and 1000 men/year this would mean, that one should adapt the recruitment facilities accordingly, which would not be desired. In order to get the proper strategies, not exercising the oscillations, the six state automaton A is defined which identifies the strategies with undesired oscillations in flows between state variables, where the set of states is S ={ S 0, S 1, S 2, S 3, S 4, S 5}, the comparison alphabet A ={ g , e , l }, the initial state is = S 0 and the set of end states is T ={ S 0, S 1, S 2, S 3, S 4}. The transition function of A , 5 : S x A ^ S is defined by the table.
Six state automation transition table
|
g |
l |
e |
|
|
↔ S 0 |
S 1 |
S 2 |
S 0 |
|
← S 1 |
S 1 |
S 3 |
S 1 |
|
← S 2 |
S 4 |
S 2 |
S 2 |
|
← S 3 |
S 5 |
S 3 |
S 3 |
|
← S 4 |
S 4 |
S 5 |
S 4 |
|
← S 5 |
S 5 |
S 5 |
S 5 |
canonical form

wastage
-
Fig. 1. Structure of the System Dynamics model of manpower system
function automaton(r) { var t = 1; // starting value for t is set to 1
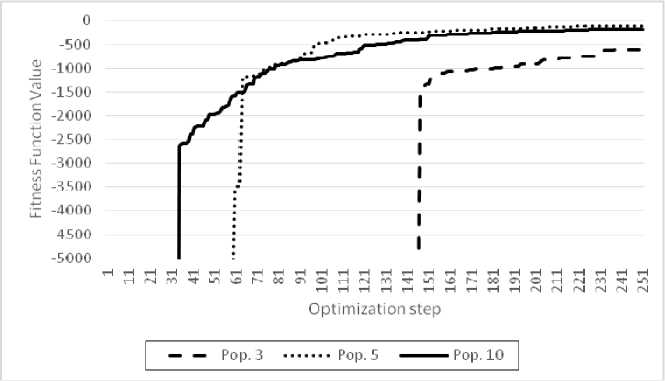
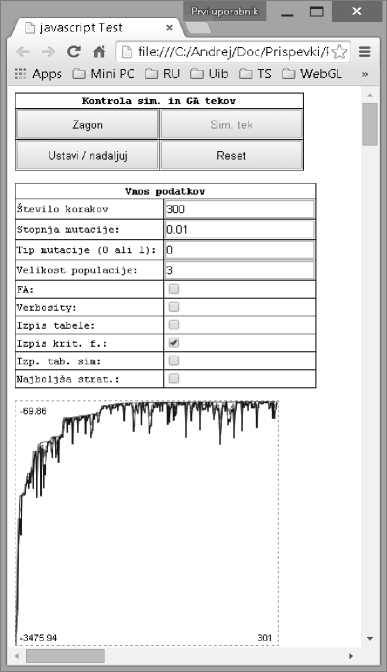
for (var i=0; i if (r[i+1] < r[i]) { // the value in the next step is lower than at present; going down t = 2; } if (r[i+1] > r[i]) { // the value in the next step is higher than at present; going up t = 4; } } if (t == 2) { // if t=2, it means, that in the previous step we went down if (r[i+1] > r[i]) { // and at the next step, we went up t=3; } } if (t == 3 break; // forbidden combination i.e. oscillation in the control strategy } if (t == 4) // we went up in the previous step if (r[i+1] < t=5; r[i]) { // and go down in the next step } } if (t == 5) { // if value is first up and then down if (r[i+1] > r[i]) { // and if we go up again at the next step t=0; // we get forbidden combination break; } } if from the beginning of the loop till the end no condition is fulfilled t does not change; meaning r[i+1] = r[i] } if (t==0) { t=10; // we set return value as 10, which is the multiplication factor } else {t=1;} // if there were no forbidden moves, the value of the return multiplication factor is 1 return t; } Fig. 2. Finite automata code realized in JavaScript The described automaton in table A is defined by the following code in JavaScript, which is shown in fig. 2. All the possible states are checked by the set of conditional clauses. Description in the code provides the explanation of particular parts. Realization of the system is shown in the fig. 3 [11]. The system consists of the GA part as well as of simulation part. Initially, the reading of the values from the Graphical User Interface (GUI) is performed. The system main loop is started, following the conversion of decimal values to binary values since the algorithm works on the converted binary numbers. This is needed, since the parameters are from continuous number set. In the next step the computation of the Fitness Function (FF) is performed. The input vector for the simulation model is prepared and simulation is started for the prescribed number of simulation time steps. At each new simulation run the model is reset. After simulation stop time is reached, the results are either evaluated with FA in order to punish the oscillations or not, which is also one of the options. After the simulation is performed, the minimum and maximum in the population is determined. The fitness vector is then normalized in order to use it at the roulette wheel selection for the new population generation. The crossing of the genomes follows with the elitism selection in order to transfer the best solution to the next population. After the new matrix is formed the mutation is done. In the next step the output of the results is provided. The Main Loop then continues until the final number of steps in the optimization procedure is achieved. In the next step the elapsed time is printed out as well as results and corresponding graphs. Fig. 4 shows example of the results comparing the desired trajectory and achieved solution for three ranks. The optimization was run with the population of size 10, mutation rate 0.01 with applied FA for 250 timesteps. The optimization time was 206s. The time could be significantly improved by the decreasing the size of the population, for example the run with the population size 3 would take 35s providing similar results however, the convergence of the optimization should also be considered. Since the mobile devices are limited in the processing power, we have investigated the influence of the population size to the convergence of the optimization procedure. We have applied three different sizes of population, 2, 5 and 10 and perform four optimization runs for each. Fig. 5 shows the average value of the fitness function for different population size. Value 0 would mean 0 deviation from the desired values. One can observe, that the population of size 5 or 10 provides approximately the same convergence however, the population of size 3 converges rather slowly. Nevertheles, the average time of the optimization is significantly different; for Population of size 3 the optimization time is 36s, for Population of size 5, 116s and Population of size 10 228s. Therefore the smaller population size might lead to acceptable solutions quicker however, too small population would converge rather slowly. Fig. 3. GA with included SD simulation model and optional FA for elimination of oscillatory solutions Realization of the optimization system. The prototype realization of the SD manpower transition model with GA as well as finite automaton was done in JavaScript. The speed of the solution search depends on the mobile device applied which is satisfactory for the smaller problems. Important aspect here is, that the model with the optimization could easily be accessed and applied in the cloud. Fig. 6 shows actual screenshot of the realization of the Genetic Algorithm with Finite Automaton in JavaScritpt running on the mobile phone. One could observe the call of the code from the server meaning, that the same code could be distributed and used on any mobile device running JavaScript. This includes all modern mobile phones as well as other smart devices such as Smart TVs etc. This is convenient for the easy application of the system for the determination of manpower strategies with various simulation models [12–15] not only from the field of manpower management. There are also other benefits, for example possibility of development of parallel algorithm on embedded devices with the node.js technology [16]. Since the mobile devices are limited in processing power, the code could also be run on the server which would significantly improve the time performance of the system. Fig. 4. Example of the results comparing the desired trajectory and achieved solution Fig. 5. Results of the experiment with different population sizes (10 – left, 3 – right) Fig. 6. Realisation of the Genetic Algorithm with Finite Automaton in JavaScritpt running in the browser Conclusion. Application of the prescribed trajectory function provided the reduction of the optimization problem of searching for the proper strategy in hierarchical manpower system. Here we assumed the exponential approach to the desired states. The addition of the described finite automaton was efficient at the elimination of strategies that examined oscillations. The implementation of the model as well as genetic algorithm with finite automata was successfully performed in JavaScript providing several benefits at the implementation, especially possibility to easily run the same code on the server, in parallel or on the embedded devices. Performed experiments show that careful selection of the population size might lead to better time performance of optimization. Directions of the future research include an automation of the optimization procedure adjustment through the genetic algorithm self-configuration [17; 18] or the use of the swarm optimization cooperative method [19] as well as the automated identification of the dynamic system from the description of their state [20].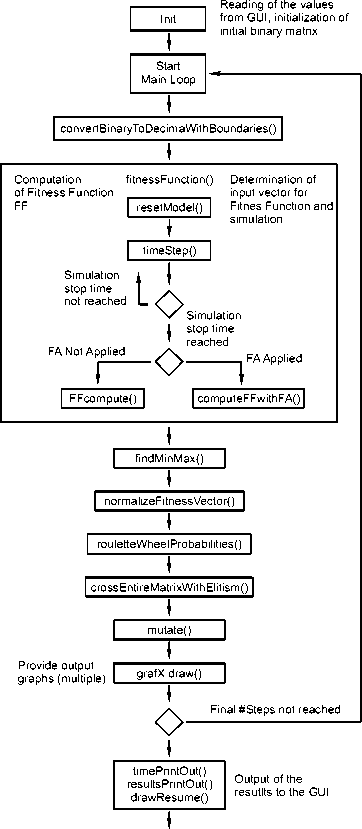


Список литературы Application of finite automata with genetic algorithms in JavaScript for determination of manpower system control
- Škraba A., Kljajić M., Papler P., Kofjač D., Obed M. Determination of recruitment and transition strategies. Kybernetes. 2011, vol. 40, no. 9/10, p. 1503-1522
- Mehlman A. An approach to optimal recruitment and transition strategies for manpower systems using dynamic programming. Journal of Operational Research Society, 1980, vol. 31, no. 11, p. 1009-1015
- Semenkin E., Semenkina M. Stochastic Models and Optimization Algorithms for Decision Support in Spacecraft Control Systems Preliminary Design. Informatics in Control, Automation and Robotics, Lecture Notes in Electrical Engineering. 2014, vol. 283, p 51-65, Springer-Verlag Berlin Heidelberg
- Akhmedova S., Semenkin E. Co-operation of biology related algorithms. 2013 IEEE Congress on Evolutionary Computation, CEC 2013, p. 2207-2214
- Bavec B. Web Realization of Genetic Algorithms for Determination of Control Strategies on Hierarchical Manpower Model. Master Thesis. 2013
- Reeves G. R., Reid R. C. A. military reserve manpower planning model. Computers & Operations Research. 1999, vol. 26, p. 1231-1242
- Škraba A., Koložvari A., Kofjač D., Stojanović R. (2014) Prototype of speech controlled cloud based wheelchair platform for disabled persons. IEEE Embedded Computing (MECO), 2014 3rd Mediterranean Conference on. DOI: DOI: 10.1109/MECO.2014.6862683
- Node.js. Available at: http://nodejs.org/(Accesed: 7.11.2014)
- Rozman Č., Pažek K., Kljajić M., Bavec M., Turk J., Bavec F., Kofjač D., Škraba A. The dynamic simulation of organic farming development scenarios-A case study in Slovenia. Computers and Electronics in Agriculture. 2013, vol. 96, p. 163-172
- Škraba A., Kljajić M., Kljajić M. B. The role of information feedback in the management group decision-making process applying system dynamics models. Group Decision and Negotiation. 2007, vol.16, no. 1, p. 77-95
- Škraba A., Kljajić M., Leskovar R. Group exploration of system dynamics models -is there a place for a feedback loop in the decision process? System Dynamics Review. 2003, vol. 19, no. 3, p. 243-263
- Kljajić M., Bernik I., Škraba A. Simulation approach to decision assessment in enterprises. Simulation. 2000, vol. 75, no. 4, p. 199-210
- Giles K. 2006. Where have all the soldiers gone? Russia's military plans versus demographic reality. CSRC, ISBN 1-905058-92-6
- Kilaz I., Onder A., Yanik M. Manpower Planning and Management in Cyber Defense. Proceedings of the 13th European Conference on Cyber warefare and Security: ECCWS 2014. Eds.: Liaropoulos A., Tsihrintzis G. Academic Conferences Limited
- Armenia S., Centra A., Cesarotti V., De Angelis A., Retrosi C. Military Workforce Dynamics and Planning in the Italian AirForce. Proceedings of the 30th International Conference of the System Dynamics Society, July 22-26, 2012, St. Gallen, Switzerland
- Škulj D., Vehovar V., Štamfelj D. The modelling of manpower by Markov chains -a case study of the Slovenian armed forces. Informatica. 2008, vol. 32, no. 3, p. 289-291
- Semenkin E., Semenkina M. Self-configuring genetic programming algorithm with modified uniform crossover. IEEE Congress on Evolutionary Computation (CEC 2012). 2012. P. 6256587
- Semenkin E., Semenkina M. Self-configuring genetic algorithm with modified uniform crossover operator. Lecture Notes in Computer Science. LNCS 7331. Part 1. 2012, p. 414-421
- Akhmedova S., Semenkin E. Co-operation of biology related algorithms. IEEE Congress on Evolutionary Computation (CEC 2013). 2013, p. 2207-2214
- Ryzhikov I., Semenkin E. Evolutionary strategies algorithm based approaches for the linear dynamic system identification. Lecture Notes in Computer Science. 2013, vol. 7824 LNCS, p. 477-484


