Application of Modified Ant Colony Optimization (MACO) for Multicast Routing Problem

Published Online April 2016 in MECS

In networking terms [3] means the process of sending a packet from one sender to multiple receivers with a single transmit operation. The concept of multicasting is useful for many applications like the transfer of the audio, video and text of a live lecture to a set of distributed lecture participants, teleconferencing application that is shared among many distributed participants, multiplayer games. A. J. Frank, L. D. Wittie, and A. J. Bernstein [9] described six techniques: flooding where packets are broadcast over all links, separate addressing where a separately addressed packet is sent to each destination, multi-destination addressing where variable sized packet headers are used to send a few multiply addressed packets, partite addressing where destinations are partitioned by some common addressing locality and packets are sent to each partition for final delivery to local hosts, singletree forwarding in which a single tree spans all nodes of the group, and multiple-tree forwarding where each member may have a different spanning tree.

Multicast routing [4] problem is often associated to multicast tree [5] problem to look for minimal cost which has been already proved to be an NP-Complete problem, without the solution of polynomial time. Ant colony optimization algorithm, among heuristic algorithms, is popular for multicast routing problem.

Greedy algorithm like Dijkstra algorithm is used from a long time to find the best path but it waste a lot of time in computation for large number of nodes. To meet the requirement of problem effectively is worse on using such algorithm.

Ant Colony Optimization algorithm is well established optimization technique for solving combinatorial problems. It takes inspiration from the behavior of real ant colonies and which was first used to solving NP-Complete problems, Travelling Salesman Problem. The first ACO system was introduced by Marco Dorigo [1] called Ant System. Here we discuss the most successful variants Ant System, MAX-MIN Ant System and Ant colony system respectively.

The first ACO algorithm proposed is an ant System where in each iteration, the pheromone values are updated by all the m ants that have built a solution in the iteration itself. The pheromone value is updated as shown in Equation (i) .

τ _ij ← (1- ρ ). τ _ij + ∑^m_k=1 ∆ τ ^k _ij (1)

Where ρ is evaporation factor and ∆ τ ^k _ij is equal to Q/L_k (Q is a constant and L_k is the length of the tour by ant k) if ant k use edge (i , j) otherwise 0.

MAX-MIN Ant System is an improvement over the original Ant System. Its characterizing elements are that only the best ant updates the pheromone values and that the value of the pheromone is bound. The pheromone updated as Equation (ii):

τ ij ← [(1- ρ ). τ ij + ∆ τ ^best ij ] ^{τ max} τ min (2)

Where ∆ τ ^best _ij is equal to 1/L_best if (i , j) belong to tour otherwise zero and τ _max and are respectively the upper and the lower bound imposed on the pheromone. L best is the length of the tour of the best ant. This may either the best tour in current iteration or the best tour found since the start of algorithm.

Ant Colony System [2] introduces the concept of local pheromone update in addition to the pheromone update performed at the end of the iteration. The local pheromone update is performed by all the ants to the last edge traversed as shown in Equation (iii):

τ ij = (1 - ϕ ). τ ij + ϕ . τ 0 (3)

where ϕ is the pheromone decay coefficient and τ 0 is initial pheromone level.

The main goal of local update is to diversify the search performed by subsequent ants during an iteration means by decreasing the pheromone concentration on the traversed edges ants encourage other ants to choose other edges and hence to produce different solutions.

The remainder of this paper is organized as follows:

In section II the problem definition has been discussed. Section III describes the research methodology. Section IV contains the proposed Modified Ant Colony Optimization technique. Section V deals with and results and discussions and finally the conclusions are drawn and scope of future study is discussed in Section VI.

• II.    Problem Defination

Multicast routing is a dynamic combinatorial optimization problem. This problem lies in the class of NP-hard problem and cannot be solved in polynomial time. Many heuristic techniques [15][16][17][18] [19][23][24] were proposed to solve this problem. Out of these researchers are fascinated to ACS for its successful implementation [10][11][12][22] and satisfactory results. Since ACS has some limitations [20][21] on pheromone initialization and convergence speed, the objective of this paper is to minimize these drawbacks.

The communication network is viewed as a graph G(V,E), where V denotes the set of nodes and E denotes the set of links between nodes in network. The multicast routing problem is to find a multicast Steiner tree T(V T ,E T ), where V T is the subset of V which have {S,[D]}. S is the source node and [D] is the set of destination nodes.

The objective is to minimize ∑ e belongs ET ƒ (e), where, ƒ (e) is the cost related to the edges in the path and E T is set edges in multicast tree T(V T ,E T ).

• III.    Research Methodology

ACO is a stochastic search method having strong robustness, suiting distributed computing and positive feedback mechanism [6]. ACO inspired by the foraging behavior of real ants. Initially wander randomly and deposit pheromone on the chosen path between the colony and food source. Rest of the ants follows the paths according to the intensity of the pheromone deposited on the path.

Transition rule for choosing the path by ants is as shown in Equation (iv):

P ij = ([ τ ij ] ^α . [η ij ] ^β )/ ( ∑ s ∈ allowed [ τ is ] ^α . [η is ] ^β )      (4)

Where

τ ij = pheromone of edge(i,j)

η_i j = visibility of edge(i,j)

α = relative importance of the track

β = relative importance of visibility

In the conventional ant colony optimization ant chooses the next node on the basis of maximum probability among the probability of the edges which are associated with the adjacent nodes of the current node. The proposed model is modified by multiplying the number of ants on the current node with the probability of edges of adjacent nodes.

After selecting the next node say j from the current say i of local update is applied:

τ ij = (1 - ϕ ). τ ij + ϕ . τ 0                 (5)

where,

τ _ij = pheromone value on (i,j) edge by an ant.

τ ₀ = initial pheromone value

ϕ = pheromone decay

The main goal of local update is to diversify the search performed by subsequent ants during the iterations.

After completing the search process the best path among all are explored and the global update is applied in order to increase the pheromone concentration on the edges which belongs to the best path. Our modification in global update formula is as shown in Equation (vi):

• τ _ij    ← τ _ij + (1- ρ ). τ _ij + ∑^m_k=1 ∆ τ ^k _ij           (6)

where,

• (i)    ∆ τ ^k ij is equal to q/L k if ant k use edge (i,j) otherwise 0 (ii) q is constant and (iii) L_k is the length of the tour of k^th ant.

This modification shows a sizeable effect on the convergence speed [7] of the algorithm.

To solve the multicast routing problem and to generate the cost function three prime attributes are considered (i) Bandwidth (ii) Latency time and (iii) Bit Error rate.

• A.    Bandwidth(B)

Bandwidth refers to the data rate supported by a network connection or interface. It is measured in terms of bits per second (bps). Bandwidth represents the capacity of the connection. The greater the capacity, performance will greater. This means it is inversely proportional to our cost (C) objective function.

• B.    Latency time (L t )

Latency is another element that contributes to network speed. The term latency refers to any of several kinds of delays typically incurred in processing of network data. A low latency network connection is one that generally experiences small delay times, while a high latency connection generally suffers from long delays. For better performance minimize the latency time is required as it is directly proportional to the cost of links in network.

• C.    Bit Error rate (BER)

The error rate is the degree of errors in the transmission of data due to bad hardware or noisy links. The higher the error rate the less reliable the connection or data transfer will be. This can also be measure as Bit Error Ratio (BER). BER is the number of erroneous bits received divided by the total number of bits transmitted. Hence we have to select such link whose BER is less and is directly related cost.

Objective function is formulated as:

ƒ (e) = 1/B + L t + BER (7)

Where B is Bandwidth Lt is Latency time and BER is Bit Error rate. Objective function f(e) need to minimize in order to provide good QoS (Quality of Service) [13][14] within the network proposed. QoS ensures the resource reservation control mechanisms and service quality by maintaining high bit rate, low latency and low bit error probability.

• IV. Modified Ant Colony Optimization

The flowchart of proposed Modified Ant Colony Optimization technique for Multicast Routing is shown in Figure 1. The source node (s_node) is initialized with m number of ants and set s_node as current node (c_node). Then the probability ‘p’ is calculated for all adjacent nodes of current node and multiplied by the number of ants at current node to get the number of ants in adjacent node. This indicates the number of ants travel in a particular edge. Insert this edge in path matrix(path[][]), which is a 2-dimensional matrix that contain the paths explored. Local updation is performed as shown in (5) to diversify the search at this point. Finally, repeat the steps of calculating probability and number of ants to adjacent nodes till the paths for destination node/nodes are explored. When the current node is same as destination node then the best path is chosen from the path[][] matrix and global updation as shown in (6) is performed on the edges which are included in the best path. The whole process is repeated until we arrive a path having all ‘m’ number of ants or maximum (90% of m) number of ants.

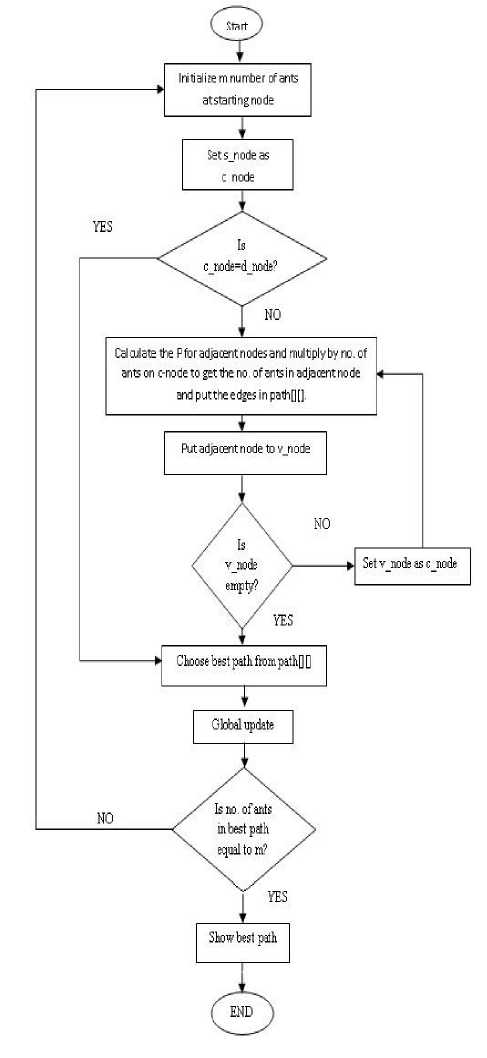
Fig.1. Flow chart of proposed ACO

• V. Results and Discussions

Let us consider a graph having 6 vertex and 12 edges as shown in Figure 2.The Node 1 is considered as the source node and node 3,4 and 5 are considered as the destination nodes.

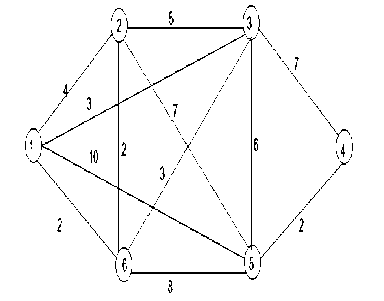
Fig.2. Graph G1(V,E)

The vertex represents the nodes of network and the edges are the links between the nodes in network. At starting we place m (here 10 in this case) number of ants at the source node of the graph. Now as ant moves from one node to another node it lay some pheromone on path. Initial pheromone ( τ ) is considered as reciprocal of initial weight between two nodes. After setting initial values and setting the m number of ants at the starting node transition rule is applied to determine the probability of next move. Then local update is applied to diversify the search among all search space. On the basis of cost related to paths best path (having low cost) is selected and global update is applied to increase the intensity of pheromone on the promising paths. It is observed that the convergence rate of proposed MACO is faster than the conventional ACO.

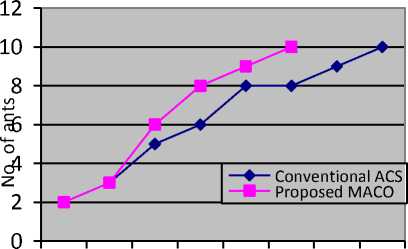
1st 2nd 3rd 4th 5th 6th 7th 8thNo. of iteration

• Fig.3. Iteration wise convergences of ants in shortest path

Figure-3 shows the iteration wise convergence of ants in the best path (1-3-5-4) for the network shown in Figure 2.

The MACO takes 6 iterations to converge all ants in the best multicast path whereas conventional ACS takes 8 iterations to converge. It is also observed that the number of ants initialized has no significant impact on the performance of the algorithm if the ants considered are greater than the number of nodes in the network.

To analyze the execution time, four more networks with different number of nodes (varying from 5 to 7) and number of edges (varying from 9 to 16) are considered as shown in Figure 4. It is observed that our proposed MACO consumes less convergence time on optimal path than conventional ACS for the different considered networks as shown in Table 1. It is found that for the small size network with less number of nodes and edges the execution time for MACO is slightly better than conventional ACO. It is our observation that for higher number of nodes and edges the difference in time consumed clearly indicates the potentiality of our proposed MACO.

	1	2	3	4	5
1	0	4	5	20	6
2	4	0	7	3	2
3	5	7	0	6	X'
4	20	3	6	0	8
5	6	2	X	8	0

	1	2	3	4	5	6	7
1	0	3	4	6	X	X	X
2	3	0	z	3	8	X	X
3	4	X	0	2	X	3	X
4	6	3	2	0	1	2	X
5	00	8	X	1	0	z	4
6	X	X	3	2	z	0	3
7	X	z	X	X'	4	3	0

(ii)

	1	2	3	4	5	6
1	0	4	8	X	10	3
2	4	0	3	14	5	6
3	8	3	0	12	3	6
4	X	14	12	0	15	20
5	10	5	3	15	0	7
6	3	6	6	20	7	0

	1	2	3	4	5	6	7
1	0	3	5	8	X	9	12
2	3	0	10	X	15	1	7
3	5	10	0	4	0	4	4
4	8	8	4	0	7	X	5
5	8	15	0	7	0	12	X
6	9	1	4	X	12	0	10
7	12	7	4	5	X	10	0

Fig.4. Weight matrix of (i) Graph G2 (ii) Graph G3 (iii) Graph G4 (iv) Graph G4

Table 1. Comparison of proposed and conventional ACO

Graph	No of Edges	No of Nodes	No of Ants	Execution Time(ms)
				Proposed MACO	Conventional ACO
G1	9	5	10	120	148
G2	12	6	10	218	244
G3	8	7	20	292	345
G4	14	6	20	249	426
G5	16	7	20	280	465

The graphical representation of Table 1is shown in Figure 5, where horizontal axis represents the networks with ant initialization, and vertical axis represents the execution time in milliseconds. For the increased number of nodes from 5 to 7 with a slight variation of edges, the performance in execution time for our proposed MACO increases considerably. The networks containing more number of diversified paths by increasing the number of edges produces better performance in terms of time consumed for our proposed MACO.

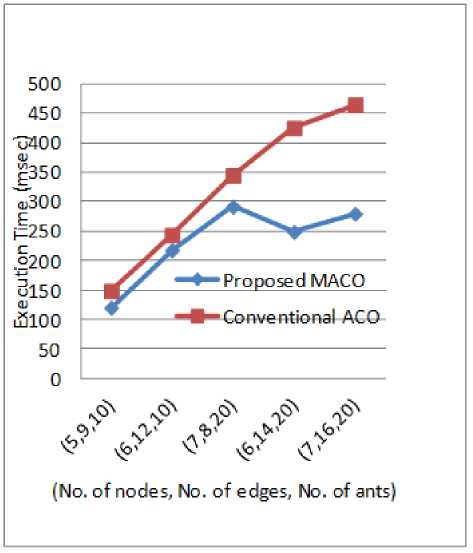
(No. of nodes, No. of edges, No. of ants)

73400 £350 a>300 p250 •|200 ol50 CD i2100

Fig.5. Comparison of proposed and conventional ACO

• VI. Conclusion

The Multicast routing is a real world dynamic problem and the aim of the paper is to construct multicast path efficiently with less time. Thus approximation and heuristic algorithms plays an important role in this field. In last few years the popularity of ACO increases due to its simplicity and potentiality. The novelty of our proposed Modified Ant Colony Optimization is the speedup of convergence to explore better paths by modification on the two parameters of conventional ACS namely (i) initialization of pheromone and (ii) local updation. The results and comparisons in Section V clearly indicates that the Proposed MACO has a better performance in terms of iterations consumed and convergence speed for the multicast routing problem with respect to conventional ACS.

It is our belief that the developed modification could be applied to other applications like Vehicle Routing Problem, Job Shop Scheduling Problem, Constraint Satisfaction Problems and many more where ACS has been successfully implemented.