Application of statistical methods for solving problems of construction materials science

T he creation of effective materials and optimization of technological processes involves the use of modern methodologies for studying the conditions for the formation of a material’s microstructure (including selforganizing nanostructures), as well as the possibility of evaluating its properties by conducting experiments in production or in a technological laboratory. An obvious but implicit factor is the material and time spent on conducting experiments that are the basis for creating a material or optimizing its properties [1–3].

It is possible to optimize the number of experiments and, consequently, the consumption of materials, energy, and time using statistical methods for organizing and processing experimental results, mathematical modeling, and analytical optimization of the results obtained [4–5].

Mathematical planning of an experiment is an important part of solving technological problems on a computer for finding equations of mathematical models of technological processes or phenomena. The correct choice of a model or simulation system is, in many cases, the basis for making the right decisions on the implementation of the experiment, both in terms of achieving its results and in

RESEARCH RESULTS OF RESEARCHERS terms of saving costs for its implementation. Methods of organizing and planning a multi-factor experiment are also essential: when constructing incomplete quadratic and quadratic mathematical models, using full and fractional factor plans that meet the optimality conditions [6–8].

The resulting dependencies (regression equations or algebraic polynomials) allow us to evaluate the influence of each of the factors on the result. In particular, the use of such methods makes it possible to assess the joint influence of various factors on the result [9–11]. This makes it possible to estimate the probability of synergistic and antagonistic effects. As practice shows, it is these effects (the effects of the joint influence of various process parameters) that underlie the emergence of self-organizing nanostructures at the micro level, which are checked using “fine” research methods.

The resulting models and the developed research methodology fully correspond to the development priorities of the construction industry, including the recommended development of digital technologies, the formation of analytical databases and computer visualization of construction processes.

The use of digital methods can significantly increase the reliability of obtaining results in the process and during processing of experimental data, use statistical methods to assess the reliability of models and the significance of the influence of factors, and at the same time significantly reduce the material costs of implementing experimental studies. This is an indirect, but very significant contribution to improving the energy efficiency of construction technologies [12–14].

On the other hand optimization of material formulations or manufacturing processes is also a form of energy efficiency improvement and is already implemented in applied tasks. An example of such an applied implementation of the developed methodologies is their application to concrete technology and, in particular, to the disposal of waste from the production of mineral binders, concrete, and construction scrap. The need to dispose of such materials follows, firstly, from the fact that any waste from concrete production contains a certain (or rather an indefinite but definable) percentage of unreacted Portland cement, and, secondly, the need to preserve such scrap leads to the alienation of significant territories, which negatively affects the environmental parameters of the environment and reduces the possibility of useful use of such territories.

The world and domestic experience of waste disposal indicates the possibility of using concrete scrap in road fillings, for leveling territories, or as a filler or filler in construction materials for various purposes [15–17]. The article presents the results of experimental studies aimed at developing a method for selecting compositions of composite material based on fine-ground waste of concrete scrap, mineral binder and super plasticizer, carried out using statistical methods.

The basis of the experiment on the example of which the implementation of statistical methods is considered was the assumption that increasing the strength and durability of concrete can be achieved by improving the quality of the contact zone and using polymers that increase the elasticity of the formed contacts. This is achieved by pretreating the aggregate with a complex additive, as well as using a polyurethane polymer group that is cured by moisture vapors contained in the air.

METHODS AND MATERIALS

The methodology of the experiment is based on a system analysis that includes the following elements: – Research of technology and processes of its components;

• –    Study of the formulations and formulations of the compositions and raw materials;

• –    Situational analysis and model type selection;

• –    Development of an experiment planning strategy, selection of factors, responses, and optimization parameters;

• –    Conducting and processing experimental results, as well as testing statistical hypotheses;

• –    Optimization of experiment results;

• –    Engineering interpretation of the experiment results.

The research is based on the methodology of THE NRU MGSU, which is based on conducting an experiment in three stages with an analytical assessment of the results (the fourth stage) [18, 19].

At the first stage, a comprehensive analysis of the research object is carried out: the technology as a whole or its individual components, including those related to the solution of prescription issues (selection of the composition of the initial compositions, for example). Factors of influence are divided into two groups: deterministic (the value can be precisely set for each situation) and variable (the change of which can be estimated by mathematical statistics).

At the second stage, an experiment is performed (active, passive, or combined), in which all the established variable factors are involved. The factors in the experiment (X₁, X₂ ... X _j ) are used in encoded form that is, reduced to the interval [–1, +1]. For example, a fractional replica from a full three-factor experiment (2³) allows you to estimate the linear influence of 7 factors, and a full four-factor experiment-the linear influence of 14 factors.

A series of experiments is implemented according to a plan, the matrix of which is a fractional replica of an incomplete quadratic equation of a higher order. In this case, the coefficients for mixed interactions are assigned the value of variable factors.

RESEARCH RESULTS OF RESEARCHERS

After conducting the experiment and processing its results, regression equations are obtained, in which the influence of each factor on the result is estimated by the coefficient at X₁, X₂, X _i . As a result, a group of the most significant factors with the highest coefficients in absolute value (usually from three to five coefficients) is determined.

At the third stage, a series of experiments is carried out, the plan of which is based on the matrix of a complete quadratic 3...5 factor experiment (according to the number of selected most significant factors).The obtained regression equations are checked for all statistical hypotheses and the models’ adequacy is checked by the Fisher criterion. As a result of statistical checks, only significant factors are left out as a result of comparison with confidence intervals (∆ bj ), and as a result of testing using the Fischer criterion, a conclusion is made about the adequacy (or inadequacy) of the obtained models.

At the fourth stage, the obtained equations are analyzed and the influence of various factors on the result is estimated, analytical optimization of regression equations and engineering interpretation of the results are performed.

Evaluation of the influence of each factor on the result is carried out by the value and sign of the coefficient facing the factor (its linear value or quadratic function) or their pair interaction. It should be noted that the experiment is carried out in coded values of factors (reduced to the interval [–1, +1], so the coefficients for paired interactions allow us to conclude only about the joint influence of these factors on the result and the direction of this influence, as well as the possibility, but not about the magnitude of synergistic or antagonistic effects. These effects can only be detected by using the natural values of the factors in the regression equation.

Interpolation of the results consists in calculating the strength and average density of the material depending on the values of the variable factors and is carried out by implementing computer programs. This program includes the following blocks: input data (values of factors in real terms), a block coding factors, calculation block, and the output results on the display.

The equations are optimized using an analytical method. Which is based on the following provisions: the obtained regression equations adequately describe the technological process under study; each equation is an algebraic function of several variables (by the number of significant variable factors) and mathematical analysis methods are used to study this function.

RESULTS

Based on the results of the implementation of the first and second stages, the costs of cement, fine-ground waste, screening, plasticizer and reinforcing component were taken as variable factors. Water consumption is set in accordance with the w/c and is not an independent factor. The response functions are the compressive strength of concrete (Y1) and its average density (Y2).

As an optimization parameter at the third stage of the experiment, the coefficient of structural quality of concrete (KCC) was adopted, which is equal to the ratio of the compressive strength of concrete (Y1) to its average density (Y2):

KCC = (Y1)/(Y2)

The experimental conditions of the third stage are presented in table 1. The consumption of the reinforcing component is assumed to be constant and equal to 1.0%

Mathematical processing of the experimental results allowed us to obtain regression equations for compressive strength (Y₁) and average density (Y₂).The significance of the coefficient was checked by confidence intervals, respectively, the confidence interval for the density was ∆ b ₁ = 0.8 MPa, and for the average density ∆ b ₂ = 3 kg/m³.

The following mathematical models (polynomials) are obtained):

• –    for compressive strength

• Y₁ = 32.7+3.7Х₁+1.6Х₂+1.9Х₃+1.5Х₁Х₃–1.1Х₂²;

Table 1.

The intervals of variation of factors

Name of the factor	Symbol Xi	Average value of the factor, i	The range of variation, ∆Хi	The values of the factor levels
				–1	+1
Consumption of Portland Cement, kg/m3	X 1	450	50	400	500
The consumption of plasticizer, kg/m3	X 2	2	0.5	1.5	2.5
Consumption of fine milled waste, kg/m3	X 3	650	50	600	700

RESEARCH RESULTS OF RESEARCHERS

• – formediumdensity:

• Y₂ = 1930+52Х₁+24Х₂+32Х₃+11Х₁Х₃–6Х₂².

The obtained models are checked for adequacy by the Fisher criterion. The calculated values of the Fischer criteria are equal for the average density model F1 = 15.2 and for the compressive strength model F2 = 15.7.Table of criteria values, respectively, equal to the 19.2 and 19.3. The calculated value of F-test do not exceed the table, and with the appropriate confidence level (98%) model can be considered adequate. This fact will be taken into account in the analytical optimization of mathematical models.

DISCUSSION

Analysis of the coefficients of the equation Y₁ = f ₁ (X₁, X₂, X₃) shows that the strength of the composite binder increases with increasing costs of Portland cement, plasticizer and fine-ground secondary bkton in the intervals taken in the experiment (positive coefficients for X₁, X₂, X₃).

When the polymer costs increase, first there is an increase in strength, and then at high costs – there is a decrease (coefficients at X2 and X22). This suggests that the function Y1 = f1 (X1, X2, X3) has a local extreme in X2, and analytical optimization can be applied.

Analysis of the coefficients of the equation Y₂ = f ₂ (X₁, X₂, X₃) shows that the greatest influence on the increase in concrete density is exerted by an increase in the consumption of Portland cement and dropout (coefficients at X₁ and X₃). Analysis of the coefficients of the equation Y₂ = f ₂ (X₁, X₂, X₃) shows that the greatest influence on the increase in concrete density is exerted by an increase in the consumption of Portland cement and dropout (coefficients at X₁ and X₃).

Analysis of the coefficients of the equation Y₂ = f ₂ (X₁, X₂, X₃) shows that the greatest influence on the increase in concrete density is exerted by an increase in the consumption of Portland cement and dropout (coefficients at X₁ and X₃).Increasing the consumption of plasticizer helps to increase the density: at first, intensive, and at high costs – insignificant.

For the equations of both strength and average density, the pair interaction at X1X3 is significant. The “plus” Sign for the value of the pair interaction factor suggests the possibility of a joint strengthening effect on the result due to the interaction of fine phases of the binder and secondary concrete containing some unreacted clinker minerals.

The technique under consideration, which is based on a cybernetic system called “black box”, is limited only to external interactions and obtaining dependencies that link the result and variable factors, but does not consider the internal processes occurring in such systems.

The results of research by Russian and foreign scientists show that in such highly dispersed systems, effects can occur due to the interaction of components at the micro level with the creation of organized structures. If the effects are aimed at improving the properties of the material, then the purpose of “fine” research is to study the possibility of prescription or technological enhancement of these effects by forming self-organizing nanostructures. If the interaction effect is aimed at deterioration of properties, then research is needed that minimizes, in this case, the negative influence factor. In this case, it is already necessary to apply the entire apparatus and methodology of nanostructure research.

We can say that the use of statistical methods perform the function of “scissors” (or blades) Occam, allowing you to cut off the excess at the technological stage without resorting to “thin” expensive research.

In particular, according to experiments on modified concrete using waste conducted in the technological laboratory, it was found that for strength and average density, the pair interaction at X1X3 is significant, which indicates a possible synergistic effect due to the interaction of fine-dispersed phases of the binder and concrete waste containing some unreacted clinker minerals. Accordingly, the directions of further scientific research are to study the possibility of forming nanostructures in the interaction of components of binder and fine-ground secondary concrete.

Analysis of the polynomial describing the relationship between compressive strength and variable factors shows that this function (which is essentially a function of several variables) for one of these variables, namely, polymer consumption (Х2), has a local extreme. Therefore, we can use the mathematical apparatus of analytical local optimization.

Analytical optimization is based on the fact that the functions for strength and density Y₁ = f ₁ (X₁, X₂, X₃) and Y₂ = f ₂ (X₁, X₂, X₃) are mathematical and mathematical analysis methods can be applied to them, provided that the adequacy condition is not violated. In this case, the following scheme is adopted:

– the equation Y₁ = f ₁ (X₁, X₂, X₃) is differentiated by X₂ and equated to zero, determining the extreme of the function Y₁ by X₂;

– solve the functions Y₁ = f ₁ (X₁, X₂, X₃)and Y₂ = f ₂ (X₁, X₂, X₃) for X₂ = opt and perform local optimization.

Analytical optimization includes the following sequence of actions:

• 1.    Analytical optimization includes the following sequence of actions: Y₁ = f ₁ (X₁, X₂, X₃) by X₂:

• 2.    We calculate the value of the natural value of the plasticizer consumption (corresponding to the possible

• 3.    We calculate mathematical models (polynomials) for the optimized value of the factor X₂ = 0.73:

  – for compressive strength: Y₁ = 33.5+3.7Х₁+1.6Х₃+ 1.5Х₁Х₃;

  – for medium density: Y₂ = 1944+52Х₁+32Х₃ +11Х₁Х₃.

∂Y1/∂Х2 = 1.6–2.2Х2 = 0 → Х2 = 1.6/2.2 = 0.73.

RESEARCH RESULTS OF RESEARCHERS maximum compressive strength of polymer concrete) using the decoding formula:

X 2 =X₂+∆Х₂•0.73 = 2.0+0.5•0.73 = 2.36±0.02 kg/m³.

The graphical interpretation of the received dependencies consists in the representation of the received dependencies Y₁ = f ₃ (Х₁, Х₃) and Y₂ = f ₄ (Х₁, Х₃) with the optimized value of X₂ in the Cartesian coordinate system (X₁, X₃) and the response function as a variable parameter: Х₁ = φ₁ (Х₃, Y₁) and Х₁ = φ₂ (Х₃, Y₂). Then go from the encoded values of the variable factors to the natural values of the factors.

Interpolation solutions for the entire range of changes in the consumption of Portland cement and the consumption of fine-ground waste (factors X1, X3) with an optimized value of factor X2 (optimal plasticizer consumption 2.36±0.02 kg/m3) are presented graphically (Fig. 1) in the form of a monogram.

The Nomogram can be used for predicting properties or selecting the composition of finishing concrete, solving direct (example I) or inverse problems (example II).

For example, to evaluate the properties of polymer concrete with a fine-milled waste content of 670 kg/m3 and a Portland cement consumption of 450 kg/m3, follow the steps shown in the red line in Fig. 3 (example I); the compressive strength (R = 31.6 MPa) and the average density of concrete (ρ = 1864 kg/m3) are determined by interpolation. To get the consumption of polymer concrete components with the specified compressive strength R = 32 MPa and an average density of 1870 kg/m3, you need to perform the steps shown in the blue line in Fig. 1 (example II). We get the consumption of Portland cement 472 kg/m3, and the permissible consumption of fine-ground waste 645 kg/m3. Then we carry out control mixes and check the experimental calculation data obtained.

CONCLUSIONS

The use of statistical methods, the methodology of planning and processing the results of the experiment allows us to obtain mathematical dependencies (models) and involves checking both the main statistical hypotheses and the significance of coefficients and effects from their pair interactions, and thus makes it possible to predict further research at all levels.

If the effects are aimed at improving the properties of the material, the goal of the next stage of research is to study the possibility of prescription or technological enhancement of these effects by forming self-organizing nanostructures. If the interaction effect is aimed at deterioration of properties, then research is needed that minimizes, in this case, the negative influence factor. In this case, it is necessary to apply the entire apparatus and methodology of research of self-organizing nanostructures, interactions at the level of which can be the cause of the identified macro effects.

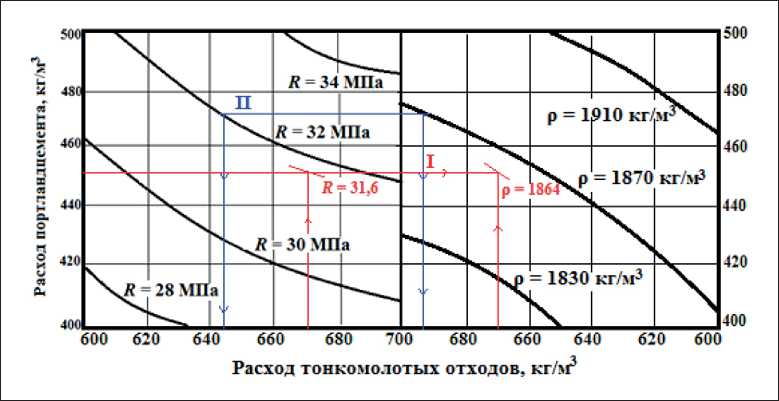
Fig. 1. Nomo gram for evaluating the properties of concrete based on its waste composition (example I) and determining the consumption of Portland cement and fine-ground waste for concrete with a given strength and density (example II)

RESEARCH RESULTS OF RESEARCHERS

If the systems are highly dispersed, then such systems may exhibit effects due to the interaction of components at the micro level with the creation of organized structures. According to experiments on modified concrete using waste, conducted in the technological laboratory, it was found that for strength and average density, the pair interaction is significant, which indicates a possible synergistic effect due to the interaction of fine-dispersed phases of the binder and concrete waste containing some unreacted clinker minerals. Accordingly, the directions of further scientific research are to study the possibility of forming nanostructures in the interaction of components of binder and fine-ground secondary concrete.The experimental methodology described in the article was tested when analyzing technologies and selecting recipes for various building materials, including binders and concretes based on secondary products and waste obtained as a result of renovation of objects removed from the housing stock. The results obtained and the databases generated at the same time fully comply with the recommendations for digitalization of construction technologies.

The results of scientific research on the development of composite binder compositions allow us to form the basis for selecting its composition of composite binder.