Application of the Rise Feedback Control in Chaotic Systems

Published Online May 2014 in MECS

Due to complex behavior of chaos, this topic attracts several attentions of scientists. Because of unpredictable and irregular behavior of this phenomenon, many attempts have been made to analyze the chaos. Because of complexity of the chaos dynamic it is treated as a bench mark for control purposes. The properties of these complex nonlinear models are studied in electrical circuits [1], biological [2] and laser systems [3]. However several attempts are made to decrease the destructive effect of the chaos.

A pioneering work in chaos control is fulfilled by OGY [4]. In [5] and [6] adaptive control are gained whilst [7] uses back stepping technique to control the chaos. In the same manner, a new controller called RISE feedback will be used here in tracking task as an alternative approach.

This controller was primarily introduced in 2004 [8] whilst inspired from super twisting- [9] as a second order sliding mode (SMC) controllers to improve their shortcomings. This controller is eventually found independent to relative degree of system as a main feature of this controller. However an auxiliary aim is to verify the capability of the controller in different classes of nonlinear systems. Meanwhile the chattering effect will be shown improved with respect to sliding mode controller.

Successfully the RISE technique is applied on different plants, in combination with neural network as a feedforward controller for a robot [10]-[11]. In [12] the same strategy is implemented on Rotor-craft base UAV. In the current work the goal is to stabilize two chaotic systems of Duffing and Genesio-Tesi via RISE technique. The work will also be followed in a tracking purpose together with the stabilization. The rest of the paper is organized as follows:

In section 2 specifications of RISE controller is described. Section 3 introduces dynamics of Duffing system chaotic whilst the RISE controller is designed to control the system in two set point and tracking tasks. Likewise a more complex system called Genesio-Tesi is controlled in section 4. In order to verify the significance of the RISE technique, the second design will be compared with an optimal controller by means of simulation. Finally a conclusion ends the work in section 5.

• II.  Robust Integral of the Sign of the Error

(RISE) feedback

Consider the following single input-single output nonlinear system [8]:

m ( x ) x ⁽ n ) + f ( x ) = u y = x

Where x (t) = [x (t) x (t).............x (n 1)(t)T eRn denotes the system state vector, y (t) e R is the output and u (t) e R is the control input signal. In order to propose the RISE technique, tracking error is defined as follows:

• ^e1 = ^xd ^{— x                                    (2)}

Where x d e L ^ and e 1 ( t ) e R denote the reference signal and the tracking error respectively. Furthermore the following auxiliary errors are defined using the derivatives of successive errors by:

• ^e 2 = ^e 1 + ^e 1

e 3 = e 2 + e 2 + e 1

• •                                                       (3)

•

• ^en = e n - 1 ^{+ e}n - 1 ^{+ e}n — 2

The RISE control law [8] is introduced as follows:

u (t ) = ( k s + 1)e_n (t ) — ( k s + 1)e_n (0)

t

• + J [( k s + 1)ae n (т ) + в sgn(e_n ( t ))] d т

⁰                                                      (4)

Where k_s , a and в are controller gains whilst sgn(.) denotes the sign function. It should be noted that the gain k_s is intentionally added by unity i.e. ( k_s + 1); instead of some K_s for the stability requirements [8]. Although this term is several times are used, gains of the error terms differ by other a and в coefficients in (4). However, the first two gains are chosen the same to make the initial error zero. Furthermore these avoid occurring discontinuity in the control effort at the beginning. In the following performance of the controller on Duffing and Genesio-Tesi systems will be investigated. Moreover the quality of the second system will be compared with similar optimal controller [15].

• III.    Duffing Chaotic System

In this section the RISE controller is applied on a Duffing chaotic system in a set point problem and hence the controller is designed to track a sinusoidal signal. Consider the following state space equation of Duffing system considering x (0) = [2  2] as an initial condition

[13]:

x 1 = x 2

x 2 =— 0.1 x 2 — x 1 + 12cos t + u (t ) + d (t )       (5)

У = ^x 1

Where u ( t )is a control input and d ( t )is disturbance.

Note that for u (t ) = 0 the system behaves chaotic with the following phase portrait:

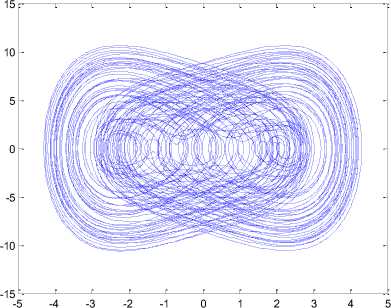
Fig. 1. Chaotic behavior of Duffing system without the control input in 250 seconds

The chaotic can be seen from the Fig.1. This dynamic will be controlled under the following two schemes of a set point and tracking purposes.

• 3.1    Set Point Problem

The RISE technique is used to control the chaos in a a nil set point problem through using an error on the x ₁ surface which is as follows:

• ^e1 = x d — x , x d = 0   ^ e 1 =— x            (6)

A successive auxiliary error is accordingly defined by:

e n = e 2 = e 1 + e 1                                  ⁽⁷⁾

However the second term of auxiliary error differs from [11] where it is multiplied by a coefficient. It is multiplied by three here and made e 2 (0) = — 8 . Substituting the recent errors in the control law (4) yields the RISE control effort as follows:

u (t ) = ( k_s + 1) e 2 ( t ) + 8( k s + 1)

t

+ J ^[( k s + 1) a e 2 ⁽ т ) + ^в sgn⁽ e ₂ ⁽ t ^))] d т

Note that parameters are chosen as e 2 (0) = — 8, k_s = 79 , a = 3.75 and в = 50 . Using the RISE control effort in the Duffing system (5) yields the following equation:

• ^x 1 = ^x 2

• x 2 = — 0.1 x 2 — x 13 + 12cos t + 80 e 2 ( t ) + 640 +

t

J [300 e 2 ( t ) + 50 sgn( e 2 ( t ))] d т + d (t )

У = ^x 1

Driving energy is originated from a nonzero initial condition. However zero state is a stable equilibrium point especially in a zero tracking (i.e. x d = 0 in 6). Besides tracking of a nonzero signal are usually of interest to provide a sufficient driving energy specifically in presence of zero initial condition. This recent RISE controller is seen stabilizing Duffing chaotic system in Fig. 2. It also guarantees zero convergence of the chaotic system states.

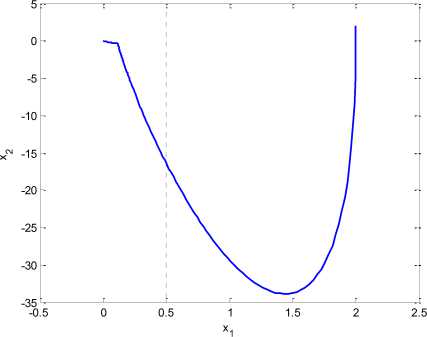
Fig. 2. Phase portrait of chaotic Duffing system using control input in 250 seconds

As from the figure can be seen the system is no longer chaotic when initiates from the initial condition X о = [2,2]' and by applying the RISE controller. The system states converge to the steady state equilibrium point i.e. X eq = [0,0]' .

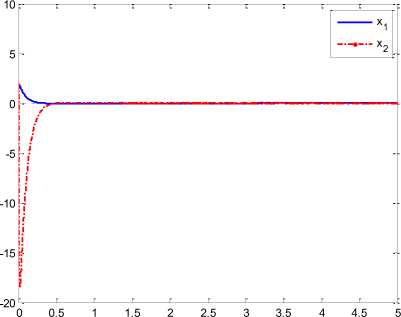
Fig. 3. Comparisons Chaotic behavior of Duffing chaotic system using the RISE control input

From Fig. 3 can be seen that the first state of system converges to zero in less than a second. Similarly the second state as a highly nonlinear state quickly converges to zero. The convergence is made possible using the following sinusoidal effort from the RISE technique.

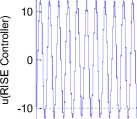
-20

-30 0

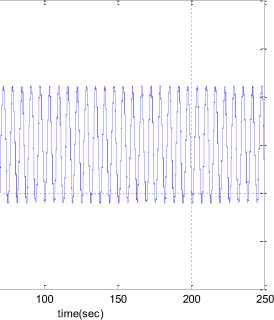
Fig. 4. Control effort in presence of the RISE controller

Satisfactory achievement of the RISE controller motivates us to investigate the quality of the application in the following tracking task.

• 3.2    Tracking Task

In order to verify the capability of the RISE technique a tracking task is of interest using the reference command of x d = sin t [14]. The error and auxiliary error are accordingly defined as follows:

e 1 = X d - x , X d = sin t ^ e 1 = sin t - x e n = ^e 2 = ^e 1 + ^e1

These also form the RISE control law which is as in the following:

u (t ) = ( k s + 1) e 2 ( t ) + 3( k s + 1)

t

⁺ J ^[( k s + 1) ae 2 ( г ) + P sgn⁽ e 2 ( r ^))] d т

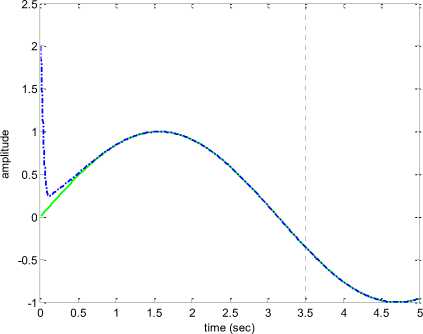
Fig. 5. Time response of state x1 as an output of chaotic Duffing system with the RISE control effort

From Fig. 5 can be seen that the RISE controller significantly performs the tracking of the sinusoidal command. The technique is found effective to converge and track the reference signal quickly. Due to desired performance of the RISE controller, the work will be followed in a more complex chaotic system, called Genesio-Tesi. Finally the achievement will be compared with those obtained using an optimal controller in [15].

• IV.    Genesio-Tesi Chaotic System

To assess the performance of the new algorithm, performance of the recent controller is investigated by applying the controller on a more complex three states chaotic Genesio-Tesi system. Three states dynamic reveal appropriate description of characteristics of a chaotic state where involving positive parameters. The dynamic of the chaotic system is as follows [15]:

x 1 = x 2

x 2 = x з x з =-c xi - bx 2 - ax 3 + x 1 + u + d

Parameters a, b and c are positive constants such that ab <  c . In this paper parameters are chosen as a = 1.2, b = 2.92 and c = 6 together with an initial condition ( - 1.8, - 1,1) [15]. In (12) u(t ) and d(t ) are control input (effort) and the disturbance respectively. The state response of the system in the three dimensional phase portrait is as follows:

-5

-10

Fig. 6. Chaotic phase portrait of Genesio-Tesi system without control input in 250 seconds

Representation of the time behavior of states is avoided to keep the length of the paper short. However, the chaotic behavior can be seen in the phase portrait. Similar to the previous section the goal is to control and to provide a zero convergence for the chaotic system using the RISE controller. The system states reveal chaotic dynamics only due to an initial condition.

• 4.1    Set Point Problem

The capability of the RISE controller will be again investigated in a set point problem. Similarly the error is defined on the surface x ₁ as follows:

e 1 = x d - x , x d = 0 ^ ^e1 =- x 1 ⁽¹³⁾

Since the system involves three states, auxiliary errors are accordingly defined in more order which is as follows:

e 2 = ^ 1 + e 1

e 3 = e 2 + e 2 + e 1 = e 1 + ^ 1 + ^ 1 + e 1 + e 1             (14)

= e 1 + 2 e 1 + 2 e 1

In order to make the convergence faster, the second and third auxiliary terms are multiplied by positive numbers two and three respectively which makes e 3 (0) = - 13.8 [11]. Using the above auxiliary errors the RISE control law is provided as follows:

u (t ) = ( k s + 1) e 3 (t ) + 13.8( k s + 1)

t

+ J [( k s + 1) ae з ( г ) + в sgn( e з ( т ))] dr

Note that parameters in (15) are chosen k s = 149 , a = 2 and в = 75 . This RISE controller alters the Genesio-Tesi dynamic system in (12) into the following equation:

• x 1 = x 2

• ^x 2 = ^x 3

x 3 = - 6 x i - 2.92 x 2 - 1.2 x 3 + x 12 + 150 6 3 ( t )

t

+ 2070 + J [300 e₃ ( t ) + 75 sgn ( e₃ ( t ))] dr + d ( t )

The phase portrait of the system in presence of the RISE controller is shown in Fig. (7).

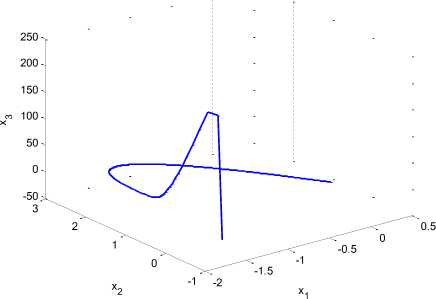
Fig. 7. Chaotic phase portrait behavior of Genesio-Tesi system with control input in 250 seconds

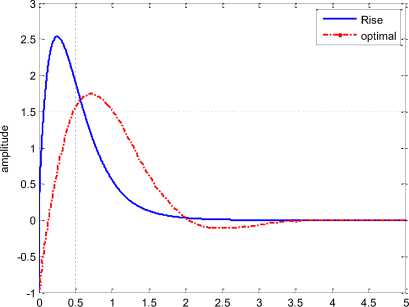
It is seen that zero convergence of the error is achieved which means the system is no longer chaotic. The system states initiates from X ₀ = [ - 1.8, - 1,1]' and converge to the steady state equilibrium point X eq = [0,0,0]' . In agreement with the achievement, convergence time of the system, using the RISE controller is comparable with an optimal controller in [15]:

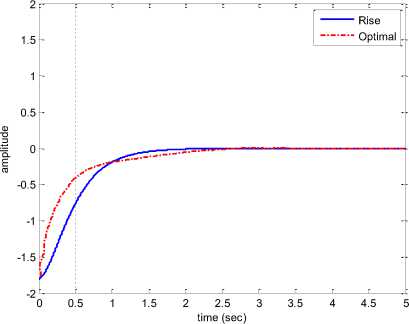
Fig. 8. The time behavior of the Genesio-Tesi state x 1 in presence of an optimal [15] and RISE controllers

It is seen that the RISE controller provides faster convergence to zero in comparison with the optimal controller [15]. Similar result is achieved for other states using the RISE controller.

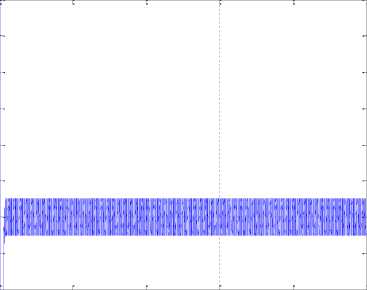
In contrast, in the third state where the state is found more complex, the performance of the RISE controller is reduced. This can be seen when it initiates from large amount. However the RISE controller converges to zero faster. All three states behaviors confirm that the RISE controller provide a fast convergence. It is also seen that the chartering is hardly occurred. The appropriate RISE input control is shown in Fig. 11.

1.5

0.5

Е

-0.5

-1

-1.5

-2

0           50          100          150          200          250

time (sec)

time (sec)

Fig. 9. The time behavior of the Genesio-Tesi state x 2 in presence of an optimal [15] and RISE controllers

Fig. 11. The RISE control input in presence of disturbance

As a result of coping with the complexity of the chattering in the chaotic dynamic, the RISE needs for a high frequency control efforts.

• 4.2    Tracking Problem

In order to verify significance of the RISE controller it is again used in a tracking problem for the chaotic Genesio-Tesi system. The reference signal is also chosen [14] x d = sin t . In this regard the error and auxiliary errors are defined as follows:

e i = X d - x , X d = sin t ^ e i = sin t — x ^e2 = ^e 1 + ^e 1

e 3 = e 2 + e 2 + e i = e i + e i + e i + e i + e i

= e i + 2 e i + 2 e i

This controller is found capable to provide the convergence in less than two seconds whilst it takes about four seconds for the optimal controller [15].

These form the following RISE control input to apply to the system:

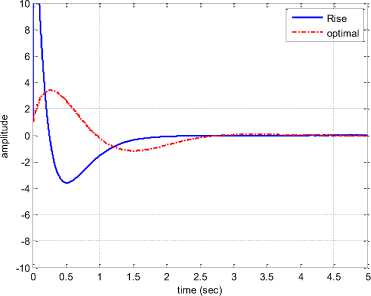
Fig. 10. The time behavior of the Genesio-Tesi state x 3 in presence of an optimal [15] and RISE controllers

u (t ) = ( k_s + i) e 3 ( t ) - 3.8( k_s + 1)

t

+ J [( k s + 1) a e з (т ) + в sgn ( e 3 ( t ))] d т

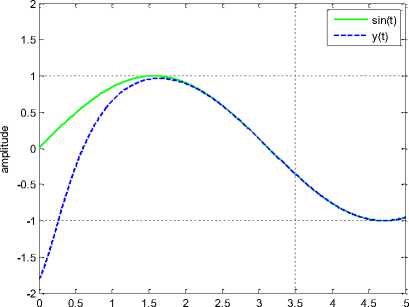
From Fig. 12 can be seen that the RISE controller is successful to track a sinusoidal command. This verifies significance of the controller to converge and follow the reference signal quickly. However a control signal with higher frequency (about three times more than the control signal in Fig. 4) must be generated.

time (sec)

Fig. 12. State x 1 as an output of Genesio-Tesi chaotic system under the RISE control action

Nonetheless recent advances in technology cope with the need for the higher frequency.

• V.  Conclusion

In this paper a new RISE controller is applied for chaotic systems for the first time. Primarily the performance of the controller is investigated on Duffing chaotic system. This controller is found capable to make converge to zero in a shorter time in less than one second. The work is followed when a tracking of sinusoidal command on Duffing system using the RISE controller was of interest. Results verify the performance of the controller in providing the convergence of the states.

The performance of this controller is also investigated on a more complex chaotic system of three states Genesio-Tesi. In this case the controller also made the states converge to zero in less than two seconds. Furthermore tracking of the sinusoidal signal is successfully achieved. Simulation results verify capability of the RISE controller whereas the controller needs generating higher frequency. Meanwhile the performance of this controller is promising in comparison with some other similar techniques.