Application of three-dimensional numerical study in air-blast atomizer designing

В настоящее время очень остро стоят вопросы удовлетворения регулярно ужесточающихся требований к экологическим характеристикам [1–3] и энергоэффективности авиационных двигателей. Обеспечение качественного распыливания топлива является ключевой задачей как для достижения целевых уровней эмиссии вредных веществ, так и для гарантии надежного розжига камеры сгорания в высотных условиях, когда распыливание существенно ухудшается.

Проблема распыливания сопряжена с разрешением комплекса научных и технических вопросов [4]. Так, например, для увеличения общего ресурса работы узлов двигателя следует снижать механический износ топливной системы [5] и, соответственно, перепад давления на форсунках, что усложняет получение качественного распыливания топлива. Необходимость уменьшения габаритов камеры сгорания, вызванная требованием снижения массы двигателя, также накладывает усугубляющие ограничения.

Разработка эффективных современных распыливающих устройств и их оптимизация значительно упрощаются при сочетании методов экспериментального и численного исследования, так как именно численные методы позволяют лучше понять структуру потока и выявить факторы, влияющие на качество распыливания в областях, недоступных для экспериментального наблюдения. Численное моделирование процесса распыливания — достаточно сложная задача, поскольку включает рассмотрение распада пленок и струй жидкости, вторичное дробление капель и их дальнейший перенос воздушным потоком. Вопросы переноса потоком сформированных капель изучены неплохо [6]. Для этого обычно применяется процедура расчета траекторий частиц в лагранжевой постановке, хорошо зарекомендовавшая себя на практике [7]. Также хорошие результаты получены некоторыми авторами при моделировании вторичного дробления капель с применением методов статистики [8]. Тем не менее адекватное математическое описание распада

жидких пленок и струй до сих пор остается сложной научной задачей, имеющиеся пути решения которой [9, 10] пока не гарантируют получения правильного распределения капель после первичного дробления.

В работе представлены результаты численного моделирования течения в каналах форсунки камеры сгорания авиационного двигателя гражданской авиации с помощью коммерческого пакета программ ANSYS CFX v14.5. Выполнен анализ расчетных параметров и проведено их сравнение с экспериментальными данными. Предложены меры по улучшению характеристик распыла у исходного варианта форсунки.

2.    Описание объекта исследования

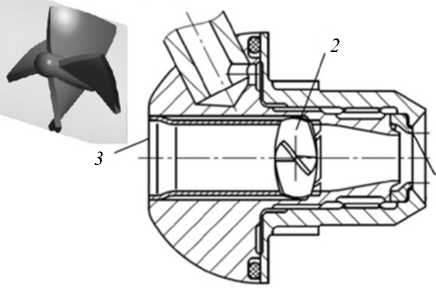
Объектом исследования является форсунка пневматического типа в сборке с внешним воздушным завихрителем 1 (Рис. 1, а ). Форсунка имеет один центральный воздушный канал с четырехлопастным завихрителем 2 . Топливо подается по каналу 3 , идет по подводящему каналу 4 и проходит через распылитель 5 по двум тангенциальным пазам, которые закручивают его сонаправленно потоку воздуха в центральном канале и наружном завихрителе. Топливовоздушная смесь выходит из форсунки через сопло наружного завихрителя 6 .

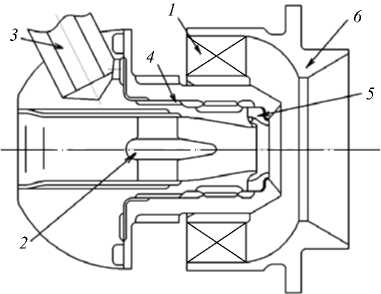
Рис. 1. Схемы форсунки ( а ) и устройства для продувки форсунок ( б ); 1 – воздушный завихритель; 2 – четырехлопастный завихритель; 3 – топливный канал; 4 – подводящий канал; 5 – распылитель; 6 – наружный завихритель

а

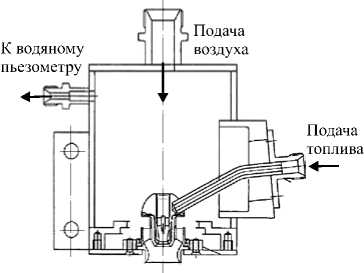
б

Данная форсунка прошла цикл испытаний по определению характеристик распыливания в ИМСС УрО РАН (г. Пермь) [11, 12]. В качестве рабочей жидкости использовалась вода с перепадами давления на форсунке 0,1 атм (режим запуска двигателя) и 10 атм при постоянном перепаде воздуха 300 мм водного столба (соответствует ~ 3% -ному перепаду на жаровой трубе двигателя) и распыливании в открытое пространство (Рис. 1, б ). Для обоих режимов устанавливалось поле скорости частиц распыленной воды, мгновенные и средние характеристики потока, а также угол факела распыливания в 6 положениях плоскости лазерного ножа, проходящей через ось конуса распыла с шагом в 30°. Также при помощи IPI (Interferometric Particle Imaging) метода [11–13] выполнялся оценочный анализ размеров частиц аэрозоля в указанных плоскостях. Экспериментальные исследования показали недостаточно хорошее распыливание жидкости представленной выше форсункой: наблюдалась струйность (выделенные направления потока жидкости), наличие существенной окружной неравномерности скорости потока, а также ухудшение качества аэрозоля при повышении давления жидкости.

3.    Постановка задачи и метод решения

С целью выявления причин, влияющих на качество распыливания жидкости, в коммерческом пакете программ ANSYS CFX 14.5 подготовлена и выполнена серия трехмерных расчетов. Для определения характеристик газовой динамики использовалось решение осредненных по Рейнольдсу уравнений Навье– Стокса методом контрольных объемов. Применялась неявная схема со вторым порядком аппроксимации по пространству (схема high resolution) и первым порядком по времени. Система уравнений Рейнольдса замыкалась с помощью SST (Shear Stress Transport) модели Ментера [14], представляющей собой линейную комбинацию к -го модели Вилкокса [15] с весом (1 - F ) и к -е модели турбулентности Лаундера и Сполдинга [16], записанной в терминах к -го , с весом F :

д , х д /      \ д ((ц )

/' + Р_к -0'р к го , д х .

— (рк) +-- р UH = ц + — дГ ’ дх^   1 ’ дх. \ а^)

j                         jk

дд

—(рго) + — д t        дxj

) н х„ 1 дк дго

■ +(1 - F) 2р-----       +а

I               Сго3го дx дХ1

го Рк -взРГО2, k

где р — плотность; Uj — скорость; к — кинетическая энергия турбулентности; ю — скорость диссипации на единицу кинетической энергии турбулентности; цt = р к/ю — турбулентная вязкость; в', а, в , стк и стю — константы; Рк — источниковый член, отвечающий за возрастание кинетической энергии турбулентности за счет действия вязких сил Рк = цt

Г дUi д U ) д U 2 д U, (   д U,

—^L + — j —^L--- М 3 ц t—^l- + р к

^ д x j    д Xi J д x j   3 д x l (    д x l

Преимуществом этой модели являются меньшие по сравнению с к -е моделью требования к детализации пристеночной области. Для адекватного описания течения вблизи стенки с помощью к - е модели необходимо выдерживать величину сеточного числа Рейнольдса в пределах у + < 0,2, в то время как при использовании к -ю модели достаточным является у +< 2 [17]. Также, учитывая чувствительность к частотам турбулентных пульсаций, к -ю модель обеспечивает лучший перенос турбулентных параметров по потоку, но по этой же причине она оказывается очень чувствительной к заданным граничным условиям [18]. В зависимости от используемого на входе значения ю можно получить существенно отличающиеся результаты решения. Именно эту проблему в SST модели решает комбинирование к -ю модели с менее чувствительной к -е с весом

F 1 = th

4 min⁴

[ кк 500 v | max ,        ,

I в юу у ю J

4 р к

С 1 д к дю _1П-ю) max 2р---,10

I    стю2ю дxj дxj

где y

расстояние

до ближайшей стенки, v — кинематическая вязкость, а ст_ю2 — константа. В такой формулировке F 1 равняется нулю около поверхности канала и постепенно приближается к единице вне пограничного слоя.

Необходимо отметить также, что гипотеза турбулентной вязкости, которую используют обе модели, и к -е , и к -ю, подразумевает изотропный характер турбулентности, что не соответствует течению в пограничном слое вблизи стенки. В этом слое и в застойных зонах использование обеих моделей существенно завышает цt из-за больших сдвиговых напряжений и, соответственно, значительной величины источникового члена в областях с малым переносом. Более точные результаты можно получить путем введения ограничителя на турбулентную вязкость: — = a^-  , где a1 — константа, р max ( a1 ю, SF2)

F 2 = th

2 Г 2 4к max²       ,

I в'юу

500v у 2ю

а S = 72 S i S — инвариантная мера скорости деформаций, при этом

S-ij

Гд U д U, ) ---L +---j дxj    дxi

Для описания течения жидкости выбрана VOF (Volume of Fluid) модель [19]. Метод переноса объемной доли жидкости основан на предположении существования четкой границы раздела фаз. В таком случае r_w (объемная доля воды) в различных точках пространства — величина дискретная: 0 — в воздухе,

• 1    — в воде. А в ячейке объем жидкости определяется как V w = r_wV , где V — объем ячейки. В этом случае плотность смеси вычисляется через плотность воздуха ( р _a ) и воды ( р w ) как р = р w r w + р _a (1 - r w ), а импульс смеси P d _y n = [ r w р w^ ^{+ (1 -} r w )р a U a ]/² .

При численном моделировании такого течения используется двойной набор основных уравнений — уравнения движения и энергии для воды и воздуха, а межфазовый перенос находится исходя из площади поверхности контакта в ячейке A = |V r w |. В данном случае жидкость считается изотермической, то есть в уравнение энергии новые слагаемые не добавляются, а правая часть уравнения движения дополняется силой межфазового взаимодействия D_wa = C D р A|U_a - U w | ( U_a - U_w ) (где C D — безразмерный коэффициент сопротивления). Система замыкается требованием равенства статических давлений всех фаз P_w = P_a = P и уравнением неразрывности:

^р w

д ,

— (р r ) + V•^р rU )

О- \^р w w)      \^р w w w)

р a

д

( р a ^{(1 -} r w ) ) ^{+ V} • ( P a ^{(1 -} r w ^)Ua ) д t

= 0.

Выбор модели VOF обусловлен хорошими результатами, полученными рядом авторов при определении положения распада жидкой пленки с использованием данной модели [10], а также простотой ее реализации. В пакете ANSYS CFD модель верифицирована на задаче разрушения пленки воды в потоке [20].

Для определения профилей скорости потока и параметров турбулентности на входе в каналы воздушных завихрителей выполнен предварительный газодинамический расчет модели всего отсека для продувки форсунок (Рис. 2, а ) с меньшей сеточной дискретизацией при перепаде полного давления воздуха на форсунке ∆ P_В ^∗ = 10 атм. Полученные поля скорости и параметров турбулентности использовались в качестве граничных условий для расчета форсунки при моделировании распада топливной пленки.

Расчетная модель форсунки (Рис. 2, б ) содержит канал наружного воздушного завихрителя 1 и канал внутреннего воздушного завихрителя вместе с каналом подачи топлива форсунки 2 , а также часть пространства, в которое истекает двухфазный поток 3 (атмосфера).

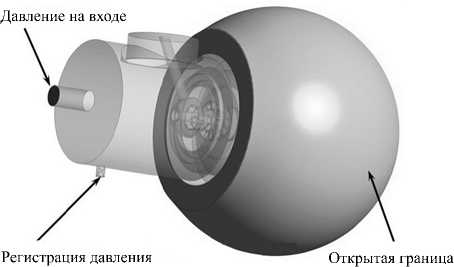
Рис. 2. Геометрия расчетных областей при газодинамическом расчете всего отсека для продувки форсунок ( а ) и при расчете форсунки по модели VOF ( б )

а

На основе представленной геометрической модели расчетной области при детальном расчете по VOF модели (Рис 2, б ) в программном пакете ANSYS ICEM CFD v 14.5 построена неструктурированная тетраэдрическая сетка (использовался алгоритм Делоне [21]) размерностью 7,5 млн узлов, 32 млн элементов. Для расчета течения вблизи стенки сетка имеет 12 призматических слоев, за счет чего среднее значение y ₊ = yu _τ I ν≈ 3 (где y — высота первой ячейки) выдержано по всем стенкам в пределах ± 1 . Для лучшего численного описания течения сетка имеет пространственное сгущение в форсунке, продолжающееся на расстояние диаметра за выходом из сопла.

На топливном входе задано давление воды исходя из перепада давления ∆ P _Ж ^∗ =10 атм.

4.    Результаты расчета

Для уменьшения времени проведения нестационарного расчета течения двухфазного потока вычисления выполнялись в параллельном режиме на вычислительном кластере. Всего было задействовано 36 вычислительных ядер с процессорами Intel® Xeon® CPU X5670 @ 2.93 GHz в течение 27 суток с применением алгоритма распараллеливания HP MPI Distributed Parallel.

Работоспособность выбранной математической модели оценивалась на основе сравнения поля средней скорости частиц в поперечном сечении факела распыла (Рис. 3). Как видно, и в эксперименте, и в расчете поток частиц неосесимметричный. В плоскости наибольшего отклонения потока от оси форсунки явно формируются три «ветви» (выделенные направления движения) с очень низкой характерной флуктуацией скорости вдоль образующих конуса распыла.

Рис. 3. Среднее поле модуля скорости капель в продольном сечении при перепаде давления воды 0,1 атм: эксперимент ( а ); расчет ( б )

1,0 0,9 0,8 0,7 0,6 0,5 0,4 0,3 0,2

0,1 0,0

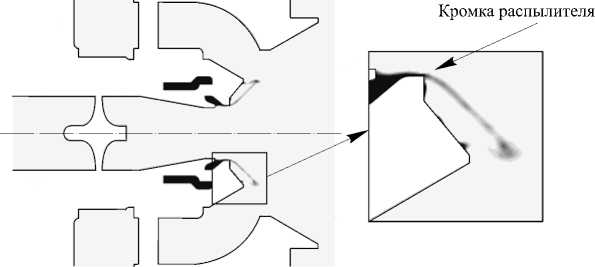
Рис. 4. Поле объемной доли жидкости в продольном сечении

На рисунке 4 в продольной плоскости расчетной области представлена вычисленная объемная доля жидкости. Угол конуса распыла, полученного расчетным путем, равняется 116 ° . Также видно, что в пленке за выходной кромкой распылителя объемная доля жидкости составляет около 0,4. Это означает, что распад жидкости на отдельные сгустки происходит уже на выходной кромке распылителя (см. увеличенный фрагмент рисунка).

Далее, на некотором расстоянии от конической втулки канала наружного завихрителя пленка встречается с потоком воздуха, идущего из внешнего контура. После этого места объемная доля жидкости резко падает до значений, меньших 0,1.

На рисунке 5 приведено изображение изоповерхности объемной доли жидкости со значением 0,025 вместе с профилем осевой скорости воздуха на выходе из центрального канала форсунки, а также распределение объемной доли жидкости в миделевом сечении сопла наружного завихрителя, осредненные по времени. Заметна существенная окружная неравномерность поля объемной доли жидкости, а также выделенные направления потока воды.

U_tll- м/с

130,0

112,5

95,0

77,5

60,0

а

б

Рис. 5. Изоповерхность объемной доли воды со значением 0,025 и поле осевой составляющей скорости воздуха на выходе из центрального канала форсунки ( а ); объемная доля воды в миделевом сечении сопла форсунки ( б )

Проявляются, по крайней мере, четыре выделенных потока капель. При рассмотрении поля осевой компоненты скорости на кромке распылителя (см. в центре рисунка 5, а ) видны также четыре области дефицита скорости. Эти области являются следами, образующимися за лопатками четырехлопастного завихрителя внутреннего контура. Вероятными причинами появления следов выделенных направлений являются:

– обдув жидкой пленки неравномерным в окружном направлении потоком воздуха в канале внутреннего завихрителя, что может приводить к неравномерному окружному распределению жидкости за форсункой;

– подача жидкости из форсунки через два тангенциальных паза.

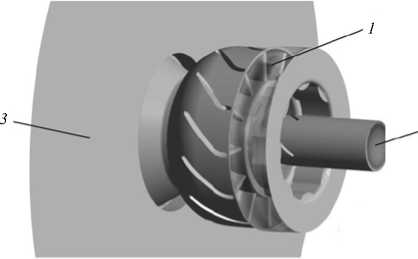
Так как изменение количества пазов при заданных конструктивных и технологических ограничениях невозможно, то в качестве основных мероприятий по улучшению качества распыливания предложено изменение аэродинамики обдува топливной пленки. Таким образом, для улучшения характеристик распыла форсунки были намечены следующие мероприятия (Рис. 6):

– снижение степени окружной неравномерности воздушного потока в сечении выходной кромки распыливающего устройства 1 за счет смещения внутреннего завихрителя 2 в сторону входной кромки внутреннего канала 3 ;

– увеличение скорости воздуха на выходе из центрального канала за счет уменьшения диаметра выходного отверстия.

а

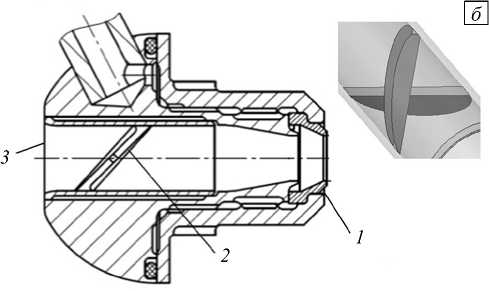
Рис. 6. Конструктивный облик пневматических форсунок: исходный ( а ) и модифицированный ( б ) варианты

Также была изменена конструкция завихрителя: четырехлопастной завихритель с центральным телом (см. увеличенный фрагмент 2 на рисунке 6, а ), определяющий сечение канала, был заменен на двухлопастной без центрального тела (см. увеличенный фрагмент 2 на рисунке 6, б ).

Ввиду высоких временных затрат на выполнение вычислений с учетом совместного течения жидкости и газа выполнялись оценочные аэродинамические расчеты модифицированного варианта форсунки для того, чтобы выявить, какое влияние оказывают предложенные мероприятия на структуру потока в каналах форсунки. Как показали предварительные расчеты, по сравнению с исходным вариантом, у модифицированного более равномерный профиль скорости в сечении кромки распылителя 1. Для сравнения на рисунке 7 показано распределение приведенного согласно следующей формуле отклонения осевой скорости U : AUпр = ((U - Uср)juср )-100% , где Uср — осевая скорость, осредненная в окружном направлении.

а

б

Рис. 7. Распределение приведенного отклонения осевой скорости: исходный ( а ) и модифицированный ( б ) варианты конструкции форсунки

5.    Экспериментальное исследование модифицированного варианта форсунки

Модифицированный вариант форсунки был изготовлен и испытан в ИМСС УрО РАН (г. Пермь). Измерениями установлено, что угол конуса распыла модифицированного варианта на 5…10° меньше угла конуса распыла исходного варианта. Предположительно, это связано с увеличением осевой скорости в центральном канале завихрителя.

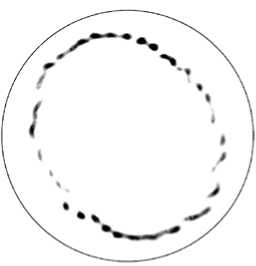
Для оценки неравномерности распыливания в окружном направлении размеры капель определялись в опросной области (фиксированной области, в которой с помощью лазерного ножа устанавливается распределение размеров частиц) на расстоянии радиуса сопла от его кромки в продольных срезах с интервалом в 30° в окружном направлении относительно оси конуса распыла.

С увеличением перепада давления подачи воды с 0,1 атм до 10 атм окружная неравномерность среднего заутеровского диаметра капель (диаметра капли, у которой отношение объема к площади поверхности равно этому отношению для всего аэрозоля в опросной области) модифицированного варианта форсунки уменьшается с 8 до 6 мкм. В то же время в исходном варианте оно почти не меняется и остается на уровне 8 мкм, хотя точки максимумов смещаются. Более подробно сравнение распределения размеров капель для исходного и модифицированного вариантов при двух углах установки лазерного ножа (под 90° друг к другу) приведено в таблице.

Таблица. Распределение заутеровского ( D ₃₂ ) и среднего ( D_m ) диаметров капель в двух перпендикулярных плоскостях, мкм

Перепад давления подачи воздуха	Вариант конструкции форсунки:	Угол установки лазерного ножа
		0°		90°
		D 32	Dm	D 32	Dm
0,1 атм	Исходный	33	26	40	29
	Модифицированный	34	25	39	29
10 атм	Исходный	41	29	39	32
	Модифицированный	40	27	39	29

Видно, что в модифицированном варианте, по сравнению с исходным, уменьшились как диаметры частиц, так и разница между значениями в различных плоскостях. Из таблицы также видно, что при незначительно отличающемся заутеровском диаметре средний диаметр в модифицированном варианте всюду меньше, что говорит о более мелком распыливании, и это дополнительно подтверждается тем, что в исходном варианте зафиксировано наибольшее количество капель с диаметрами от 28 до 38 мкм, а в модифицированном — с диаметрами от 22 до 32 мкм .

Также следует отметить, что модифицированный вариант форсунки характеризуется значительно меньшим количеством очень крупных капель, движущихся в периферийной части потока, что косвенно свидетельствует о способности модифицированного варианта к более тонкому распыливанию топлива. При визуальном контроле факела распыливания модифицированной форсунки замечено, что струйность, по сравнению с исходным вариантом конструкции, значительно снизилась (количественное сравнение окружных неравномерностей распыливания у двух вариантов конструкций затруднено ввиду отсутствия данных для исходного варианта форсунки).

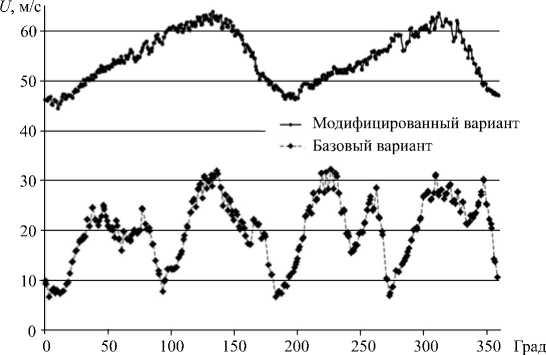
Рис. 8. Угловая развертка осевой скорости вблизи стенки

На рисунке 8 показана угловая развертка в сторону оси форсунки осевой скорости на расстоянии 30 мкм от кромки распылителя. Видно, что у модифицированного варианта значительно возросла скорость обдува пленки и снизилась относительная неравномерность ее распределения по окружности. Таким образом, мероприятия, реализованные в модифицированном варианте на основе данных численного анализа, свидетельствующих о неравномерности потока на выходе из внутреннего канала, позволили снизить окружную неравномерность распределения капель и уменьшить наблюдаемую интенсивность струй.

6.    Заключение

Проведено трехмерное моделирование воздушного и воздушно-капельного потоков в пневматической форсунке. Показано, хорошее качественное согласие между результатами численного моделирования и экспериментальными измерениями.

Расчеты показали, что распределение капель неоднородно в азимутальном направлении. Факторами, влияющими на формирование капель, являются пространственное распределение и величина скорости воздушного потока. Изменения в конструкции форсунки привели к формированию более однородного и интенсивного воздушного потока в области распылителя.

Экспериментальные измерения продемонстрировали, что модификация конструкции форсунки привела к более однородному пространственному распределению капель и уменьшению струйных эффектов.

Таким образом, с использованием VOF подхода удалось описать такое явление, возникающее при распыливании жидкости, как струйность — существенную неравномерность расхода частиц в окружном направлении, а также определить и уменьшить один из факторов, влияющих на возникновение струйности.

Работа выполнена при финансовой поддержке Министерства образования и науки Пермского края (проект № МИГ13 «Исследование закономерностей распыла жидкого топлива в высокотемпературных камерах сгорания газотурбинных двигателей. Разработка распыливающего устройства для нового авиационного двигателя»).

This work was supported by the Ministry of Education and Science of the Perm Region in the framework of the project “Investigation of the fuel atomization in the high temperature combustion chambers of the gas turbine engines. Designing of atomizer for a new aircraft engine”.