Аппроксимация автоволновых решений в моделях ламинарного пламени

Введение. Разработка действенных методов исследования автосолитонных уравнений представляет большой интерес для ряда естественнонаучных и технических приложений [1]. Простейшей формой горения является плоское ламинарное пламя, формируемое процессами различной природы — химическими реакциями и микропереносом. Результирующий процесс представляет собой бегущую волну превращений [2]. Математической моделью пламени служат нелинейные уравнения с частными производными. В данной работе развит новый подход к решению уравнения горения, опирающийся на рациональный выбор функционального вида решения и отработанную технику оптимизации.

Постановка задачи и описание моделей. Динамика автоволн горения описывается уравнением [2]:

£)^ + v —+ И/е ^(1-Т)” =0, Т(-оо) = 1, Т(оо) = 0,             (1)

в котором температура Т и энергия активации® выражены в единицах Т_ад (температуры сгорания в адиабатических условиях); n ~ 1 — эффективный порядок брутто-реакции; D, И/и v — коэффициент диффузии, предельная скорость химического превращения и скорость распространения пламени соответственно. Решение (1) позволяет определять брутто-характеристики химизма путём измерения скорости распространения пламени, его толщины и температуры. Определённые таким образом физико-химические характеристики ламинарного пламени используются при проектировании энергосиловых установок.

Приблизим реальный химический источник, характеризующийся скоростью We^e,T (1 - Г) = 0 , функцией И/аТ^₽(1-Т) : для удобства перейдём к безразмерным переменным 7 =7/7_тах и 0 = 0/7_тах . Последняя величина служит важной физико-химической характеристикой горючей смеси — своего рода форм-фактором источника, определяющим ширину благоприятного для реакции температурного интервала 7_min 4- 7_max. Независимой переменной выбрана безразмерная температура Т, которая совпадает с безразмерной концентрацией [В] продукта В одностадийной реакции В + Q^Q— тепловыделение).

‘Работа выполнена при финансовой поддержке фонда ALCOA.

Из условия совпадения максимумов исходной и приближающей функций следует связь модельного показателя ₽ с содержательной величиной ©:

3 = 0/2- 1 + (1 + 4/0)1/2

В отсутствие активации Р 0, при незначительной (по отношению к условиям в пламени) высоте энергетического барьера реакции 0 -> 0^1/2 , а в условиях, когда активация существенна, р ^ ©. Безразмерная температура Т*, соответствующая максимальной скорости реакции в точечной системе — реакторе идеального смешения равна ₽/(₽ + !). Множитель о в приближающей формуле определяется равенством аррениусовского е~^в,т и степенного оТ^₽ скоростных множителей при Т = Г*, из которого следует явное выражение:

а = (1+1/р)₽е ₽. (3)

При высоком активационном барьере выражение (3) упрощается: о~е 01. Однако практически интересен случай, когда величина 0 оказывается в пределах от одной до нескольких единиц. Модельный пример [3] с Р = 2 попадает в категорию реалистичных: ему соответствуют 0 = 4/3

и а = (3 / 2е)2.

Полученный таким способом коэффициент о следует включить в вероятностный фактор реакции И/ определяющий решение задачи (1). Поправка к скорости распространения пламени имеет химическую природу и оказывается существенной, если рассматривать горение моторных топлив. Например, для водородно-воздушных смесей величина © изменяется от ~ 2 при стехиометрическом соотношении компонентов до ~ 15 на нижнем концентрационном пределе, что требует корректировать скорость пламени. Соответствующий поправочный коэффициент близок к асимптотическому о1/2 ~ е'01'/2.

Идея предлагаемого метода решения задачи состоит в том, что сначала выбирается форма производной решения (1) по пространству, затем конструируется соответствующая функция источника, содержащая некоторые подгоночные параметры. Задача сводится к минимизации некоторого функционала совпадения (ФС) с применением стандартных численных методов.

В качестве модельных решений — профилей установившейся температурной и (или) концентрационной волны — будем выделять: 1) квазилогистические, являющиеся решением уравнения dT/dz = cj^ {1-Т^, 2) тригонометрические, отвечающие уравнению df/dz-= cp/ncos2 [п(т-1 / 2)] , и 3) квазикинетические, соответствующие профилю температуры dT/dz = с,е e,T (1 - Т), где 0'^0 и, как правило, меньше по абсолютной величине, у>1 — по рядок реакции.

Существенно, что во всех базовых моделях контур величины dT/dz представляет собой пик, расположенный в интервале дозволенных значений Т ; на краях этого интервала реализуются однородные условия (начальные или конечные). Без потери общности можно считать, что профиль температуры и (или) концентрации исходных продуктов в волне горения задаётся формулой вида <Т(т)• (1 -Т)v, где Т^Г^ — некоторая возрастающая функция, причём Т(о) = о. В последнем выражении учтено влияние энергетических и материальных факторов на структуру зоны активного горения. Выбранная математическая структура позволяет объединить все перечисленные профили волны горения, т. е. унифицировать рассмотрение. Явное выделение множи- теля (l-7")v вызвано тем обстоятельством, что горение связано с материальными ограничениями и подчиняется реакции некоторого (не обязательно целого) порядка по реагентам.

Рассмотрим волну горения с квазикинетическим профилем dTjdz^e^ (i-f)v                         (4)

как вполне реалистичную. Вторая производная искомого распределения 7(z) по независимой переменной равна d^Tldz1 =ф[07т2-у'/(1-Т)] e evr(l-T)Y' 2.                    (5)

Подстановкой (4) и (5) в уравнение (1) нетрудно убедиться, что разрешающий его в выбранном классе профилей 7(z) источник имеет вид

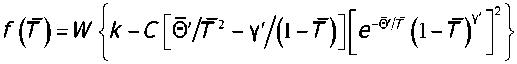
Зависимость (6) нуждается в определении подгоночных коэффициентов k, С, 0' и у'. Их нетруд но вычислить, зная вид источника f (т) = И/ eQT -7"Г ' эксп у ^ VV С у / J

Минимизировав функционал совпадения

1    _        — 2  —

®С = [[''(’’)-М7’)]                              (8)

О с учётом необратимости реакции в пламени, которая определяется ограничением на параметры к и С, обеспечивающим положительность множителя в фигурных скобках (6) при Т= 0 4-1, получаем искомые параметры модельного источника {А, С, 0', у'}. Через них выражается скорость распространения пламени и—собственное значение краевой задачи (1):

и = (WD/C^¹ к.                                   (9)

Полученный результат не связан с выбором профиля волны, а является следствием фундаментальных свойств уравнения (1) и регулярности предложенного способа его решения. Поскольку W и D — заданные константы, определение скорости горения свелось нахождению нетривиального (к* 1, С* 0, 0'^0, yV у) аппроксимирующего выражения (6).

Результаты компьютерного эксперимента. Численные эксперименты свидетельствуют о слабой зависимости эффективного порядка реакции в пламени от высоты активационного барьера 0, что позволяет с хорошей точностью считать у'»у. Кроме того, оказывается, что 0' близко к 0. Эти обстоятельства, с одной стороны, существенно облегчают определение подгоночных коэффициентов, а с другой — предоставляют основания для физической интерпретации расчётных данных. В соответствии с (6) получается приближённое решение краевой задачи (1):

I" е^е'^!т (1 - Г) dT =с/ + const, _q = (WC/Df,

0'= 0,9390 - 0,02102,                                  (10)

к = (1,028 - 0,0519у) • е °'^,г"⁰",

£ _ g 1,33+6,0690+3,555V^/3

Представление о погрешности решения (10) можно получить, сравнивая модельную функцию (6) при подстановке в неё коэффициентов (10) с исходной формой источника (7), а также само решение краевой задачи — скорость распространения пламени — с соответствующими результатами, полученными независимыми методами. Локальное отклонение предложенной модельной функции от оригинальной составляет доли процента даже при наименее благоприятном сочетании параметров 0' и у, когда максимальная скорость реакции реализуется при близкой к 0 или, наоборот, к 1 безразмерной температуре Т . В первом случае реализуются холодные пламена, во втором — нормальные или горячие.

Сопоставлять непосредственно приближённое решение краевой задачи (10) с найденными альтернативными способами нецелесообразно, поскольку детали профиля источника (7), следовательно, качество их аппроксимации уравнением (6) и соотношениями (10) отражается, главным образом, на определяемом формулой (9) собственном значении и. Само же решение (профиль термохимических параметров в волне горения) является интегральной характеристикой, что снижает погрешность его определения. Поэтому представительно сравнивать вычисляемое нашим методом собственное значения и задачи с полученными известными способами. В безразмерном виде й = к/С^.                                  (11)

Эта величина определялась многими авторами с использованием разнообразных методик [3]. Рассчитанная нами зависимость й = U(Q,^ приближается формулой

/7^A v^ — р⁴,⁷⁷⁸-1,⁸ббб^2/3-2,оз2у^1/3

(И)

Удобными оказываются и менее точные приближения й = (7(0, у): /7^ \Д — fl2,262-0,80596-0,446у и (7(0, у) = (1,028 - о,О519у)е5-665-3-о35®1/3-0-0™^^

Формулы (12)—(14) хорошо согласуются с классическими результатами Зельдовича — Франк-Каменецкого, Кармана и другими приближениями [2—4].

Выводы. Результаты проведённых компьютерных экспериментов свидетельствуют о том, что полученные результаты приемлемо согласуются с классическими в физике горения. Расчётным путём установлено, что сходное поведение демонстрируют все классы аппроксимирующих моделей — квазилогистические, тригонометрические и гибридные. Разнообразные модели и способы решения рассматриваемой краевой задачи приводят к близким скоростям ламинарного пламени. Этот факт свидетельствует о структурной устойчивости уравнения (1) и оправдывает применение предложенного нами нового способа решения задачи (1).

Также установлены и (или) подтверждены следующие свойства решения задачи (1), (7):

• 1)    существует стационарный режим горения, которому отвечает некоторая скорость распространения пламени и, полностью определяемая физико-химическими свойствами среды;

• 2)    среда неустойчива к параметрическим возмущениям, т. е. локальное возмущение усиливается и развивается в волну горения;

• 3)    пространственный масштаб волны нормального горения совпадает с диффузионной длиной, отвечающей времени химического превращения.