Аппроксимация двумерных законов распределения зависимых случайных величин

Данный подход исследования двумерных распределений можно использовать для различных видов распределений, но для упрощения генерации исходных данных и отладки алгоритмов рассмотрим параметрическую модель, заданную следующим способом:

<

[ X = X 1 ,

Y = 7 1 - p² • X 2 + p² • X 1 ,        (1)

где X 1 и X ₂ - независимые величины, p - коэффициент корреляции.

Ограничимся рассмотрением нормального и экспоненциального одномерных законов, а также закона Вейбулла. Исходя из линейного характера зависимости между случайными величинами X и Y , построим прямую, используя метод наименьших квадратов (МНК) :

y = ax + b .                (2)

Задача заключается в нахождении коэффи-

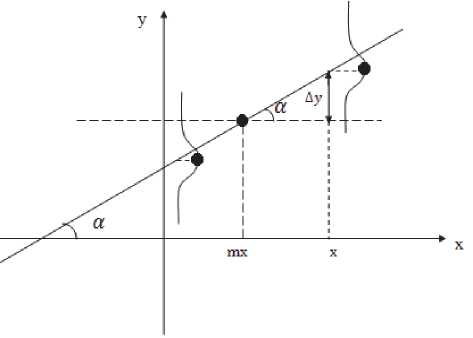
Рис. 1. Преобразование модели циентов линейной зависимости, при которых следующая функция принимает наименьшее значение [1]:

F (a, b ) = E”=i (У . - (aXi + b ))2 ^ min’ (3) где n – размер выборки, a , b – коэффициенты линейной зависимости в выражении (2), xi , yi – i-ый элемент двумерной выборки.

После определения а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. Далее двумерную выборку необходимо повернуть так, чтобы случайные величины X и Y можно было рассматривать как независимые. Получена следующая формула:

У , = y - a ( X, - mx ) ,           (4)

где a – коэффициент линейной зависимости, найденный методом МНК, mx – оценка математического ожидания, y – -ый элемент выборки по оси ординат после преобразования, y – -ый элемент выборки по оси ординат до преобразования, x – -ый элемент выборки по оси абсцисс до преобразования.

Для удобства постановки задачи классификации будем представлять случайную последовательность в виде частотной двумерной гистограммы с разбиением на M x коридоров по оси x и M y коридоров по оси y , построенной по исследуемой выборке, представленной на рис. 2.

Для восстановления аналитического выражения функции плотности вероятности из набора узловых точек используется алгоритм нейросетевой аппроксимации. Для примера, в качестве базовой модели для определения коэффициентов нормального-нормального закона распределения вероятности, который был установлен на этапе классификации, берется RBF -сеть, нейроны скрытого слоя которой являются двумерны-

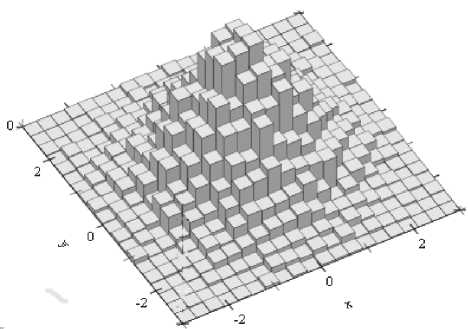
Рис. 2. Частотная гистограмма двумерной выборки

ми функциями Гаусса вида:

_- ( V x X - C x ) 2 _- ^ у У ^- c y ⁾²

G (x, y) = e    2       2 .(5)

Для нормального-экспоненциального закона распределения вероятности:

_- ^{( V} x^{x -} c x ) _- , y

G(x, y) = e    2 y .

Для нормального-Вейбулла закона распре- деления вероятности:

k_{y -} ^{( v} x^{x -} c x ⁾²

G (x, У) = p" • e

^P y

P y

Эти функции используются для построения аппроксимирующей модели, которая выглядит следующим образом:

f ( x, y ) = w • G ( x , y ) .        (8)

Неизвестные коэффициенты w , Vx , Vy, Cx, C y , Py , ky , Xy в выражениях (5-7) являются настраиваемыми, а их значения определяются в процессе обучения нейронной сети.

Таким образом, целевая функция определяется по формуле:

• 1    M x - 1 M y ^-1 _A

E=7 EE(f(x, y,)- f(x, yj))2 ^ min. (9)

• ²    i = 0 j = 0

Приведем формулы вычисления параметров для нормального-нормального закона распределения вероятности:

V = ^V x + ^ w • G^x , y ) • ^{( G ( x} , y ) ^- f ⁽ x,y j )^{) V} , x- ^{- c} x ) x,

^V y =^V y +n^ w • G ( ^x , y) • ^(G(x , y) ^- f ⁽ x,y) ^V y y , ^{- c} y ) y j , ^C x = ^C x ^- ^ ^ w • G ( ^x , y ) • ^(G(x , y ) ^{- f} ( x,y j ^{)) V} x ^x , ^{- C} x ), ⁽¹⁰⁾ c y = ^C y ^- ^ ^ w • G ( ^x , y) • ^(G(x , y) ^- f ⁽ x,y j ^{)) V} y y , ^{- C} y )•

Для нормального-экспоненциального:

^V x = ^V x ⁺^ w ^ G ( x,y M Gx,y) - f (x,y_j))^V'x_t - C x )x,

^C x = ^C x - ^ w ^ G ( x,y) ^ ^(G ) - f ( x,y , ⁾⁾⁽zx - ^C x ), (11) ^ y = ^ y + ^ ^ w ^ G ( X, y) • ⁽ GX, y) - f ⁽ x, y j ))y j .

Для нормального-Вейбулла:

^V x = ^V x + ^ ^ ^w • G(^x,У) • ^(G(x,У) ^- f ⁽ x,y_]⁾')⁽ x x ^{- - C} x ) x, ^C. = ^C x ^- ^w • G ( ^x , y ) • ^(G(x,У) ^- f ⁽ x,y)) ⁽^ x ^{- C} x Y y k y

Py = Py -^^ w• G(x,y)• (G(x,y)- f (x,,y,)) jy, Py y ky (12)

k y = k y -П^ w • G ( x,y) • ( G ( x,y ) - f ( x, у , ))1п( у , .)(1 - y j- ).

P _y

Оценка погрешности аппроксимации вычис-

Таблица 1. Результаты исследования методов

СКП m x СТ x m + 3ст xx max 1 0,0137 0,0038 0,0243 0,0246 2 0,0144 0,0008 0,0169 0,0160 3 0,0116 0,0035 0,0221 0,0224 4 0,0231 0,0029 0,0318 0,0309 ляется по формуле:

A = [f (f (x, y) - f( x, y))2 dxdy. (13)

D

Для исследования погрешности было проведено 29 испытаний [2]. Также, полагая величину погрешности случайной величиной, распределенной по нормальному закону, величина погрешности оценивается по правилу “трёх сигма”. В каждом из испытаний строилась гистограмма 15 на 15 столбцов и моделировалась выборка случайной величины, состоящая из 10000 отсчетов и распределенная по двумерному нормальному закону. Результаты исследования представлены в табл. 1.

Первая строка – погрешность, полученная с использованием методов описанных в статье, вторая строка – результаты исследования погрешности аппроксимации RBF-сетью [3].

Третья строка – результаты, описанные в [4], последняя строка – результат использования метода моментов.

В таблице m x представляет выборочное среднее погрешности аппроксимации, рассчитанное по 29 значениям, СТ - корень выборочной дисперсии, max – максимальная величина погрешности среди проведенных испытаний.

Таким образом, по результатам испытаний, которые приведены в таб. 1, можно сделать вывод о том, что метод, описанный в статье, имеет меньшую погрешность, чем метод моментов, однако большую, чем метод, основанный на аппроксимации RBF-сетью [3], и метод, используемый для работы с двумерной независимой выборкой [4].