Аппроксимация уравнений с частными производными 4-го порядка в классе кусочно-полиномиальных функций на треугольной сетке
Автор: Клячин Алексей Александрович, Клячин Владимир Александрович
Журнал: Математическая физика и компьютерное моделирование @mpcm-jvolsu
Рубрика: Моделирование, информатика и управление
Статья в выпуске: 2 т.22, 2019 года.
Бесплатный доступ
В настоящей работе определяется уклонение кусочно-кубического почти-решения бигармонического уравнения и выводится общая формула его вычисления. На основе данного понятия получена аппроксимация уравнения. Проведен ряд численных расчетов с целью экспериментального подтверждения полученной формулы.
Кусочно-кубическая функция, почти-решение, бигармоническое уравнение, аппроксимация уравнения, уклонение кусочно-кубического почти-решения
Короткий адрес: https://sciup.org/149129860
IDR: 149129860 | УДК: 517.951, | DOI: 10.15688/mpcm.jvolsu.2019.2.5
Текст научной статьи Аппроксимация уравнений с частными производными 4-го порядка в классе кусочно-полиномиальных функций на треугольной сетке
DOI:
Доктор физико-математических наук, заведующий кафедрой компьютерных наук и экспериментальной математики, Волгоградский государственный университет ,
Дадим необходимые определения. Пусть задана многогранная ограниченная область Q С R ” . Рассмотрим произвольное разбиение этого многогранника на невырожденные тетраэдры Т 1 , Т 2 , ..., T n и пусть М 1 , М 2 , ..., М т — все вершины этих тетраэдров. Будем предполагать, что ни одна из точек М г не является внутренней точкой ни одной грани тетраэдров. Через Г / будем обозначать грани всех тетраэдров, I = 1,2, ...,L, а максимальный диаметр всех тетраэдров обозначим через h, т. е. h = max diamT ^ .
В настоящей работе определяется понятие уклонения почти-решения бигармониче-ского уравнения в классе кусочно-полиномиальных функций на треугольной сетке. На основе этого определения выводится простая формула вычисления уклонения и экспериментально подтверждается на нескольких примерах.
1. Понятие почти-решения бигармонического уравнения
В работе [3] вводится понятие почти-решения для эллиптических уравнений, которое для уравнения минимальных поверхностей
■'“" ^'(.х^ )=• будет выглядеть следующим образом. Функция / G W 1,P(Q) называется почти-решением уравнения минимальной поверхности в области Q С R”, если найдется е > 0 такое, что для любой функции h G Cd(Q), |h(x)| < 1 в Q, выполнено
Ω
(У /, V h )
X i v / | 2
dx
< е .
Наименьшая из величин е > 0, которую будем обозначать eq(/), удовлетворяющая этому определению, называется уклонением почти-решения /(x). Другими словами, eq (/) = sup / , ^"^ dx q V Vi+W где точная верхняя грань берется по всем функциям h G Cd(Q) таким, что |h(x)| < 1 в Q. Отметим, что если функция / G С2(Q) и eq(/) = 0, то функция / является решением уравнения (1) в области Q.
В работе [1] на основе данного определения было введено понятие уклонения кусочно-линейного почти-решения уравнения (1), получена формула его вычисления на произвольной треугольной сетке. Там же доказана сходимость e q ( / l ) к интегралу
И №]|dxd^ Q при стремлении мелкости сетки к нулю для / G С2(Q), если уклонение вычисляется для кусочно-линейной функции /L, совпадающей в узлах сетки с функцией /.
Для получения уравнения, аппроксимирующего бигармоническое уравнение
Au = Й + 2
дх 4
д 4 и дх^ду 2
д 4 u
+ = О, ду4
нам потребуется несколько видоизменить приведенное определение для класса кусочнокубических функций. В связи с этим мы вводим понятие уклонения кусочно-кубического почти-решения и выводим формулу его вычисления.
Через ф г (х),г = 1,...,т, обозначим такую кусочно-линейную функцию, которая удовлетворяет следующим условиям:
Ф г (М , ) = 0 при j = г, ф г (М , ) = 1 при j = г.
Будем в качестве почти-решения рассматривать кусочно-кубические функции. Поясним сказанное.
Зафиксируем произвольное натуральное число q. Для каждого тетраэдра Т к будем строить полином следующим образом. Пусть Ак,А^ , ...,А ^ +1 - вершины этого тетраэдра. Рассмотрим набор точек
D к _ дк I ^ 1 ---Д ^ -I- -I- h l "д к Д
-°ij = А1 + q а2а1 + ... + q Ап+1А1, где г1, ...,гп = 0, ...q и г1 + ... + гп < q.
Отметим, что число этих точек R 9,n , включая вершины тетраэдра, определяется равенствами
R (q + 1)(q + 2)
9, 2 2 ,
R q,n
1 + ER
г,п - 1 ,
для n > 3.
г=1
Пусть А 1 , А 2 ,..., A R q п - все полученные точки в Т к . Зафиксируем некоторые постоянные значения u 1 , и 2 , ...u ^ q п и построим интерполяционный полином Р к9 (х) степени q такой, что
Р к (A i ) = u l , г = 1, 2,...,Rq i .
Вычисление коэффициентов многочлена Р ^ сводится к решению линейной системы уравнений. Далее считаем, что q = 3. Построенную кусочно-кубическую функцию будем обозначать через и(х).
Уклонением почти-решения и(х) будем называть величину
N Г
Е дд (м) = SUp
52 / (VAu, ^К^ах к=1 Тк где точная верхняя грань берется по всем кусочно-линейным функциям вида м К(х) = 52 КгФг(х) г=1
таким, что | К г | < 1 для всех г = 1,...,т и К г = 0 для М г Е д Q (то есть для граничных вершин).
Зафиксируем произвольно г = 1,т. Пусть Т ( ,Т 2, , ...,Тц » ) те тетраэдры, у которых вершиной будет точка М ^ . Выходящие из этой вершины грани тетраэдра T j , j = = 1, 2,...,к(г), обозначим Г * х , Г * 2 , ..., Г^ и пусть Г ^п +1 оставшаяся грань тетраэдра Т, противоположная вершине М,,. . Обозначим через v j 1 , v j 2 , ..., v jn , v jn +1 - внешние по отношению к тетраэдру TJ нормали этих граней. Так как в тетраэдре функция и кубическая, то V Au = const. Ниже \Е | означает (п — 1)-мерную меру множества Е . Тогда
k(i)
/ (V Au, V h ) dx = ^2 h i / (V Au, V y « ) dx = E h^ (V Au, V y i ) dx.
Q внутр. M i Q внутр. M i j=1 2 i
1 j
Так как для полинома третьей степени и выполнено div( V Au) = 0, то
k(i) - k(i) п + 1„
E hi E / (VAu, Vyi) dx = E hi E ^(VAu, vj,) Vi dS = внутр. Mi j=1 < внутр. Mi j=1 1=1'
1 j
. k(i) п
= п E h - EE^ v j, )i r j, | .
внутр. M i j=1 1=1
Последнее слагаемое в сумме по I равно нулю, так как функция у » = 0 на грани r jn +1 .
Преобразуем данное выражение следующим образом пп
E (V Au, v j, )| r j, | = E (V Au, v j, )| r -z| — (V Au, v j„ +1 )| r ‘,,+1 | =
1=1, п + 1 „„
= E / (V Au, v j, ) dS — (V Au, v jп +1 )| Г jп +1 | = / (V Au, v ) dS —(V Au, v jп +1 )| Г jп +1 | =
‘ jl3
= —(VAu, vjп+1)|Гjп+1|, так как интеграл равен нулю по формуле Гаусса — Остроградского. Поэтому приходим к равенству
k(i)
У (V Au, V h ) dx =
Q
— П E hi E(VAu, У,п+1)|Г*+11- п внутр. Mi j=1
Тогда
e aa ( u ) < - п
E внутр. m »
k(i)
E Очевидно, что неравенство превращается в равенство для такой функции h, которая в граничных вершинах равна нулю, а во внутренних вершинах равна k(i) hi = sgn (E(VAu, vj„+1)|rj„+1| \ j=1 Таким образом, справедливо утверждение. Теорема 1. Уклонение почти-решения /Nуравнения минимальной поверхности вычисляется по формуле =аа(«) = П Е Е пвнутр. Mi j=1
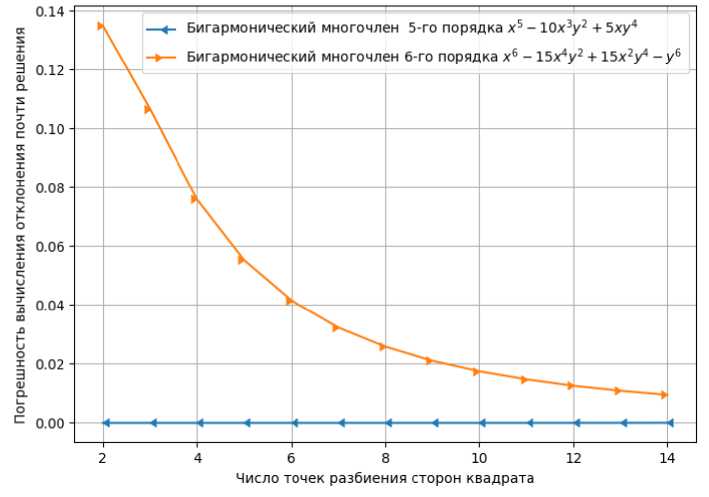
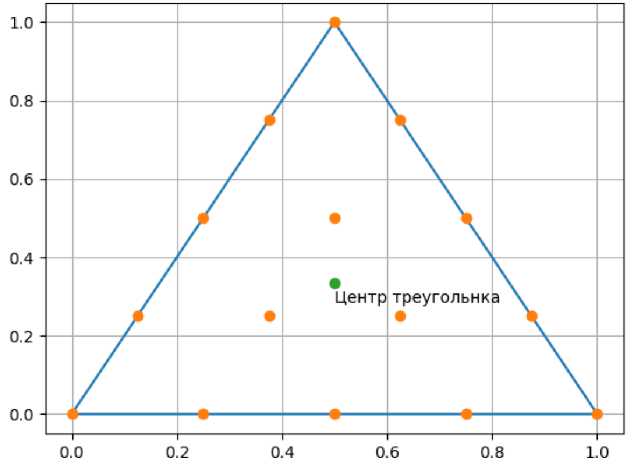
2. Экспериментальная проверка полученной формулы Рассмотрим примеры численных расчетов величины (3). Вычисления будем проводить для функций, являющихся решением бигармонического уравнения (2) в области квадрата [0,1] х [0,1]. Для осуществления вычислений стороны этого квадрата разбиваются на N частей и в каждой полученной прямоугольной ячейке строится диагональ. Таким образом мы получим триангуляцию, для которой будем проводить вычисления согласно формуле (3). В качестве инструментов проведения численных экспериментов была выбрана связка Python + NumPy. Модуль NumPy позволяет использовать ’C’-подобные массивы, которые обеспечивают уменьшение времени вычислений за счет более быстрого доступа к элементам по сравнению с обычными списками Python. Так же частично были использованы расчетные модули на триангуляциях, описанные в работе [2]. Число точек разбиения сторон квадрата Рис. 1. Результаты численных экспериментов На рисунках 1, 2 показаны зависимости вычисленной величины отклонения решения уравнения от числа точек разбиения сторон указанной квадратной области. При этом аппроксимация величины VAu осуществлялась в каждом треугольнике триангуляции с помощью многочленов 4-го порядка Р(х, у) = ах4 + Ьх3у + сх2у2 + dxy3 + еу4 + /х3 + + дх2у + hxy2 + ку3 + 1х2 + тху + пу2 + рх + qy + г. Рис. 2. Результаты численных экспериментов Для этого внутри треугольника и на его сторонах выбиралось равномерно расположенных 15 точек, как показано на рисунке 3. При этом приближенное значение VAu « VAF(x, -у) = (24ax + 6by + 4сх + 6dy + 6/ + 2h, 6bx + 4су + 6dx + 24ey + 2g + 6k) для использования формулы (3) вычисляется в центре треугольника. Рис. 3. Точки для интерполяции в треугольнике Вывод В целом для всех выбранных бигармонических функций величина уклонения Едд(и) оказалась, как и ожидалось, достаточно малой даже при сравнительно небольшом количестве узлов триангуляции. В среднем, при 25 < N< 35, абсолютная погрешность составила порядка 0,0001, что дает приблизительно асимптотическую оценку O(h2), когда шаг разбиения h ^ 0.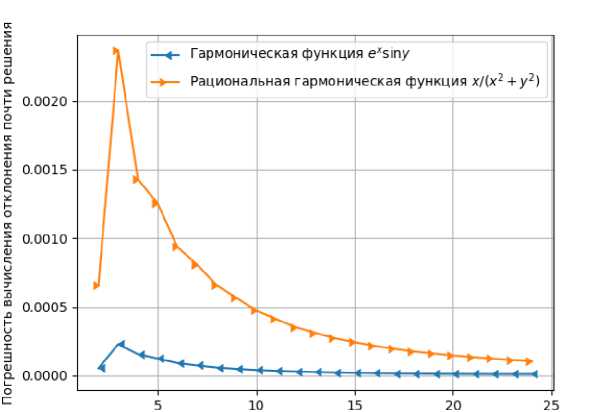
Список литературы Аппроксимация уравнений с частными производными 4-го порядка в классе кусочно-полиномиальных функций на треугольной сетке
- Клячин, А. А. О кусочно-линейных почти решениях эллиптических уравнений / А. А. Клячин // Вестник Волгоградского государственного университета. Серия 1, Математика. Физика. - 2013. - № 2 (19). - C. 19-26.
- Клячин, В. А. Численное исследование устойчивости равновесных поверхностей с использованием пакета NumPY / В. А. Клячин, Е. Г. Григорьева // Вестник Волгоградского государственного университета. Серия 1, Математика. Физика. - 2015. - № 2 (27). - C. 17-30.
- Миклюков, В. М. Геометрический анализ. Дифференциальные формы, почти-решения, почти квазиконформные отображения / В. М. Миклюков. - Волгоград: Изд-во ВолГУ, 2007. - 530 c.


