Априорные оценки решения нелокальных краевых задач для псевдопараболического уравнения
Автор: Бештоков Мурат Хамидбиевич
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 3 т.15, 2013 года.
Бесплатный доступ
В работе рассматриваются нелокальные краевые задачи для псевдопараболического уравнения третьего порядка с переменными коэффициентами в одномерном и многомерном случаях. Для нелокальных задач получены априорные оценки в дифференциальной и разностной трактовках. Из полученных оценок следуют единственность, устойчивость, а также сходимость решения разностной задачи к решению дифференциальной задачи.
Короткий адрес: https://sciup.org/14318426
IDR: 14318426 | УДК: 519.635
Текст научной статьи Априорные оценки решения нелокальных краевых задач для псевдопараболического уравнения
В настоящее время весьма активно изучаются локальные и нелокальные краевые задачи для гиперболических уравнений третьего порядка. Указанный класс задач вызывает большой практический и теоретический интерес из-за того, что прикладные задачи физики, механики, биологии сводятся к таким уравнениям. Например, вопросы фильтрации жидкости в пористых средах [1, 2], передачи тепла в гетерогенной среде [3, 4], влагопереноса в почво-грунтах (см. [5], [6, c. 137]) приводят к модифицированным уравнениям диффузии, которые являются уравнениями в частных производных гиперболического типа третьего порядка:
L(u) = (n(x, t)u xt ) x + (k(x, t)u x ) x + r(x, t)u x + d(x, t)u t - q(x, t)u = f (x, t). ( * )
Уравнение вида ( * ) часто называют псевдопараболическим. Краевые задачи для различных уравнений третьего порядка псевдопараболического типа изучались, например, в работах [7–11].
В работе рассматриваются нелокальные краевые задачи третьего порядка для псев-допараболического типа с переменными коэффициентами в одномерном и многомерном случаях. Для нелокальных задач получены априорные оценки в дифференциальной и разностной трактовках. Из полученных оценок следуют единственность, устойчивость, а также сходимость решения разностной задачи к решению дифференциальной задачи.
-
(е) 2013 Бештоков М. Х.
1. Постановка задачи
В замкнутом цилиндре QT = {(x,t) : 0 6 x 6 l, 0 6 t 6 T} рассмотрим следующую нелокальную краевую задачу ut =
(k(x,t)u
x
)
x
+ (n(x,t)u
xt
)
x
+ r(x,t)u
x
—
q(x,t)u + f (x,t), 0 < x < l, 0
l
t
n(0,t) = j e(x,t)u(x,t) dx + j p(t,T)u(l,T ) dT — ^(t), 0 6 t 6 T,
-
(1.2)
n(l,t)=0, 0 6 t 6 T,
u(x, 0) = u o (x),
0 6 x 6 l,
-
(1.3)
-
(1.4)
где
u ∈
r(0, t) = r o 6 0, r(l, t) = r N > 0, l n t (x,t) l , | r(x,t) l , | q(x,t) l , IM, C 4 , 3 (Q T ), n e c 3 , 2 (Q T ), k e C 3 , 2 ( Qt ),
0 < c o 6 n(x,t), k(x, t) 6 c 1 ,
I r x I , | в(x,t) | , | p(t,T) | 6 C 2 ,
(1.5)
r,q,f e C 2 , 2 (Qt ), e(x,t) e c [0,T],
Q T = p(t,T)
{ (x, t) : 0 < x < l, 0 < t 6 T } , П(х, t) = ku x + nu xt , 0 6 t 6 t, u o (x) e C 2 [0, l], — функция, непрерывная на [0,T] , c o , c 1 , c 2 — положительные числа.
Заметим, что нелокальное условие (1.2) можно заменить условием
α
t
n(0,t) = j e(x,t)u(x,t) dx + j p(t,T)u(l,T ) dT — ^(t),
где α — глубина корнеобитаемого слоя [12] или активный слой почвы, который участвует в водоснабжении корневой системы, в процессах испарения и транспирации. Поставленные и исследованные в данной работе задачи характерны также тем, что содержат в краевых условиях нелокальность по времени, впервые изученный А. И. Кожановым [10].
По ходу изложения будем использовать положительные постоянные M i , i = 1, 2,..., зависящие только от входных данных задачи (1.1)–(1.4).
2. Априорная оценка в дифференциальной трактовке
Допуская существование решения дифференциальной задачи (1.1)–(1.4) в замкнутом цилиндре Q T , получим априорную оценку для ее решения. Для получения априорной оценки воспользуемся методом энергетических неравенств. Умножим уравнение (1.1) скалярно на u :
(2 . 1)
(u t ,u = ((ku x ) x ,u) + ((nu xt ) x ,u) + (r(x,t)u x ,u) — (q(x,t)u,u) + (f (x,t),u), где (u, v) = Rl uvdx , k u k 2 = (u, u).
Пользуясь неравенством Коши с ε, из (2.1) получим ll dt kuk2 + dt У nuX dx + 2 У k(x,t)uX dx о о
6 2(n(l,t)u(l,t) — n(0,t)u(0,t)) + 3c 2 k u x k 2 + (3c 2 + 1) H u H o + k f k o .
Имеет место оценка [13, с. 124]
u 2 (l,t) 6 e k u x k 2 + C e k u k O , (2.3)
где e> 0 , c e = | + 1 .
Оценим первое и второе слагаемое в правой части неравенства (2.2), пользуясь неравенством Коши с ε и граничными условиями (1.3) и (1.4),
l
t
- H(0,t)u(0,t)
= — u(0, t)^ j в (x,t)u(x,t) dx + j p(t,T)u(l,T ) dT — ^(t)^
6 M 1
l u2(0,t) + M
в(х, t)u(x, t) dx
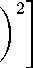
+ 2 ^ 2 (t) + M 2
t j u2(l, t) dT.
(2.4)
Из (2.4), пользуясь (2.3) и неравенством Буняковского, получим
H(l,t)u(l,t) — H(0,t)u(0,t)
t
6 M S ^ k u x k O + ku k o ) + M 4 У ( k u x k 2 + k u k O ) dT + 2 ^ 2 (t).
(2.5)
Учитывая (2.5), из (2.2) находим
l
4 k u k O + 4 / nu X dx + c o ku x k 2 ,Q t 6 M 5 f k u x k O + k u k O ) dt dt
t
+ 2M 4 У ^ k u x k 2 + k u k O ) dT + ^ 2 (t) + kf k O .
Проинтегрировав (2.6) по τ от 0 до t , тогда получим
(2.6)
где
k u k 2 + k u x k 2 + k u x k 2 ,Q t t tτ
6 M 6 У ( k u x k 2 + k u k O ) dT + M 7 У j ( k u x k O + ||uk 2 )dT 1 dT 0 00
t
+ M8^ / (kf k O + ^ 2 (T)) dT + ku O (x)k 2 + ku O (x)k2) ,
(2.7)
t kuxk2,Qt = j kux ll(O dT.
Второе слагаемое в правой части (2.7) оценим следующим образом:
tτ j J («ux«O + 00
k u k 2 0 dτ 1
t dT 6 ту (kuxkO
+
k u k 2 0 dτ.
(2.8)
В силу (2.8) из (2.7) находим
t llullO + lluxIlO 6 M9 j (kux 112 + llullO) dT
(2.9)
t
+ M 8( 1 O f k O + ^ 2 ( t ) ) dT + ku 0 (x)k O + ku 0 (x)k 2) • 0
Применяя к неравенству (2.9) лемму Гронуолла (см. [13, с. 152]), из (2.7) с учетом (2.8) получим
t llukWi(0,l) + kuxk2,Qt 6 M(t)( I (ifIIO + ^(t)) dT + kuO(x)kWi(0,l)) , (2.10)
O где M (t) — зависит только от входных данных задачи (1.1)-(1.4).
Из априорной оценки (2.10) следует единственность решения исходной задачи (1.1)– (1.4), а также непрерывная зависимость решения задачи от входных данных на каждом временном слое в норме пространства W 2 1 (0, l) .
3. Устойчивость и сходимость разностной схемы
Для решения задачи (1.1)–(1.4) применим метод конечных разностей. Для этого в замкнутом цилиндре Q T введем равномерную сетку [14]:
^hT — Dh X dt — { (xi , tj)) x G Dh, t G dt }, idh — {xi — ih, i — 0,1,..., N, Nh — l}, Dt — {tj- — jT, j — 0,1,... , m, тт — T}.
На сетке idhT дифференциальной задаче (1.1)-(1.4) поставим в соответствие разност- ную схему:
* /Т\ (ст)f
(3.1)
yt,i — Л(t)yi ■ 5y + ^i, (x, t) G DhT, aiXOyX‘,0 + Y1 yxt,0 — X esygCT) ~ + X TPsjy^NN - ^ + 2 (yt,0 + dOy0CT) - ^o) , t G DT, s=0
aNXNyXN + YTvyxt,N) — 2 yy^N + dNy(? - VN^ , t G IDT,(3.3)
y(x, 0) — Uo(x), x G Dh,(3.4)
где
л(t )y i” — X i (ay XCT) ) x,i + b i+ a i +i y XCT) + b - a i y X^ - d i y (CT) ,
5y — (Yy xt ) Xji , У (ст) — ^y + (1 - ^)y, y — y j — y(x i ,t j ), r — r + + r , b ± — rk + O(h 2 ),
| r | — r + — r , r + — 0.5 (r + | r | ) > 0, r — 0.5 (r — | r | ) 6 0, a i — k(x i - 0 . 5 ,t), Y i — n(x i - 0 . 5 ,i), d i — q(x i ,t), V i — f (x i ,t),
_ t = tj+0.5 = tj + 0.5т, xi-o.5 = xi — 0.5h, h, т — шаги сетки.
X 0 = n , 0 . 5 h | r o | , если r o 6 0’
1 + k o.5
{ T , если s = 0, s = j;
т, если s = 1,..., j — 1,
X N = 1 . 0 . 5 h | r N | , если r N > 0’ k N-0.5
{ h , если s = 0, s = N ; 2
h, если s = 1,..., N — 1.
|
1 X = 1 + R’ |
R =--—— — разностное число Рейнольдса, k |
Для получения априорной оценки воспользуемся методом энергетических неравенств. Тогда задачу (3.1)–(3.4) перепишем в другой форме
|
y t,i = X iW^ )x ,i + (Yy xt ) x,i + b t a i +i y Xx^i + b i a i y( s,i — d - y i " + V i ’ (3.5) ( o ) n ( o ) ( o ) — ( o ) . a i X 0 У Х 0 — 0.5hd 0 y 0 — L в з У ® ~ - L Tp s,j y sN + д s=0 s =0 Y 1 y xt, 0 y *'0 = 0.5h 1 0.5h ’ (3'6) — a N X N y x°N - ^hd N y N Y N y xt,N -x y *'N = 0.5h 0.5h ’ ' |
y(x, 0) = U 0 (x). (3.8)
Полагая a = 0.5 и обозначая y + y = Y , перепишем задачу (3.5)-(3.8)
|
y * = 0.5A * (t)Y + 5y + Ф, (3.9) y(x, 0) = u 0 (x), (3.10) |
|
|
где |
AY = X i (aY x)x,i + b + a i +i Y x, i + b - a i Y x , i - d i Y i , при x ^ W h ; N (CTV. j e *(+\v — a 1 X 0 Y x, o - 0 . 5 hd o Y o - E в = У ^ ~ - E T P s,j Y s,N Л (t)Y = Л - Y =--------------- 05 h s =------- , при x = 0; Л +v — -a N X N Y X,N -0.5hd N Y N _ 7 Л Y = 0 . 5 h ’ при x = l’ 5y = (7Ух* ) x,i ’ при x G W h ; 5y = < 5 - y = Y 0 y x h o , при x = 0; d + y = 7 N 0 y 5 x h 'N , при x = l,
Ф = ' v - = 0 .5h ’ при x = 0;
- i
X =(1+ 2k) ’ при x G W h ; X = < X - = (1 + S) , при x = 0, Г0 6 0;
|
Введем скалярное произведение и норму
N
[u, v] = )> U i V i ~, i =0
( h , i = 0, i = N,
( h, i = 1,...,N - 1,
N
| [u] | 2 = [u,u], н|2 = x u 2 ~ = (u,u].
i =1
Умножим теперь разностное уравнение (3.9) скалярно на Y = у + у :
[ y t ,Y] =0.5 [Л W.Y] + [5y,Y] + [Ф,У].
Преобразуем суммы, входящие в (3.11):
[y t ,Y] = 1(У — У), (У + У) =-tlyl—-tlyl = [1,у 2 ] t ,
[Л * (t)Y, Y ] = (Л Y, Y) + O.5hY o Л - Y o + 0.5 hY N Л ' Y N
= - (ax, Y x2 ] - (aY, X x Y x ) + (b + a+X Y) + (b - aY x , Y)
Nj
- [d,Y 2 ] — Y 0 ^X e s Y s ~ - Y 0 ^X Tp s,j Y N , s=0 s =0
[ 5y,Y] =(5y,Y) + 0.5 hY o 5 у + 0.5 hYN8 + у = - (Yy xt , Y x] ,
[ Ф,Y] = (y,Y) +0.5hy - Y o + 0.5 hy + Yn = (y,Y) + A
Учитывая (3.12)–(3.15), из (3.11) находим
[1,y 2 ] t = - 0.5(ax,Y x2 ] - (Yy xt ,Y x ] - 0.5 (ax x Y,Y x ) + 0.5 (b + a +1 Y x ,Y)
Nj
+0.5 (b - aY x , Y) - 0.5 [d, Y 2 ] - 0.5 Y o ^ e s Y s ~ - 0.5 Y o ^ Tp s,3 Y N + (y, Y) + ^Y o . s=o s =o
Оценим суммы, входящие в (3.16):
[1,y 2 ] t = ( |[y]| 2 ) t ,
(aX,Y 2 ] > M i (1,Y x2 ]= M i k Y x ] | 2 ,
(Yy xt ,Y x ] = (1,Y ( уХ ) t ] = (1, (Yy X ) t ] - (1,Y t y X ],
- (aX x Y, Y x ) + (b + a +1 Y, Y x ) + (b - aY, Y x ) 6 M 2 | Y x ] | | [Y] | 6 M s ( k Y x ] | 2 + | [Y] | 2 ),
- [d,Y 2 ] 6 C 2 [1,Y 2 ] = C 2 | [Y] | 2 ,
[y,Y] 6 2( | [Y] | 2 + 1И 2 ).
-
(3.11)
-
(3.12)
-
(3.13)
-
(3.14)
-
(3.15)
-
(3.16)
-
(3.17)
-
(3.18)
-
(3.19)
-
(3.20)
-
(3.21)
-
(3.22)
Справедлива следующая
Лемма [15]. Для любой функции y(x), заданной на сетке CDh, справедливо неравенство maxy2(x) 6 ekyx]|2 + f1 + 1) |[y]|2, x∈ωh ε l где ε — произвольная положительная постоянная, l — длина интервала, на котором введена сетка О h
С помощью этой леммы и неравенства Коши получаем оценку
Nj
-
- Y0 ^^ e s Y $ ~ - Y0 ^^ Tp js Y N + ^Y q s=0 s =0
(3.23)
2 j
-
6 у + M 4 (k Y x ] | 2 + | [Y] | 2) + MV (k Y x ] | 2 + | [Y] | 2) T. s =0 4
Учитывая оценки (3.17)–(3.23), из (3.16) находим:
(I[y] | 2 ) , + (1. (Yy X ) t ] + M l «Y]l 2 6 C 1 II y x ] | 2 + M g (I[Y] | 2 + « Y , ] | 2 ) j
(3.24)
+ MV (|[Y] | 2 + k Y x ] I 2)T + M 7 (и2 + м2). s =0
Умножим обе части (3.24) на т и просуммируем по j 0 от 0 до j :
j
I[yj+1]I2 + «yX+1]I2 + X М0]I2T j 0=0
-
6 M 8 X II y x ] I 2 T + M g f X ( I [Y j 0 ] I 2 + «Y x ' ] I 2 )t (3.25)
j 0=0
jjj
+ EE (I [Y j ' ] I 2 + II Y x 0 ] I 2) tt) + M io( X (MI 2 + . 2 т + I [y 0 ] I 2 + k y , ] I 2
j'=0s=0S
Обозначая F(t j ) = M io ( P j o =0 ( I И I 2 + M 2 )t + I [y 0 ] I 2 + ||y Q ] I 2 ) , из (3.25) получим
I[yj+1]I2 + |yX+1]I2T + X «Yx0]I2T 6 M8 jIIyxlpr j 0=0
(3.26)
+ F (t j )•
jjj
X (I [Y 10 ] I 2 + « Y j ' ] I 2)т + X X (I [Y j 0 ] I 2 + « Y j 0 ] I 2) TT j ' =0 j ' =0 s =o
Третье слагаемое в правой части (3.26) преобразуем следующим образом jjj
X X (I IY j ' ] I 2 + « Y x ' ] I 2) tt 6 T X (I [Y j ' ] I 2 + « Y x ' Ц2) t. (3.27)
j'=0s=0
В силу (3.27) из (3.26) находим
j
I[yj+1]|2 + kyX+1]|2 + X IY']|2T j 0=0
jj
6 M 8 £ y т + M 11 £ (|[Y j 0 ] | 2 + ||Y j 0 ] | 2) т + F(t j ).
j 0 =0 j 0 =0
(3.28)
Учитывая неравенство I[y j ' +1 + y j ' ] | 2 6 2 I[y j 0 +1 ] | 2 +2 I[y j ' ] | 2 , преобразуем выражение M 8 P j 0 =0 || b x ] | 2 T + M 11 P j 0 =0 ( | [Y j 0 ] | 2 + k Y j ' ] | 2 )т . Тогда
jj
j
= Mn X (|[yj41 + yj,]|2 + IlyX'+1 + yX,]|2)т j 0=0
j
+ M8 E ||yX'+1]|2T 6 M12(|[y'+1]|2 + kyX+1]|2)т j 0=0
(3.29)
+ M 13 E (| [y ’ ' ] | 2 + k y X ' ] | 2)т + M 14 (И2 + Ijy S ] | 2)т. j 0 =1
Подставляя (3.29) в (3.28), получим
j
|[yj+1]|2 + kyX+1]|2 + X k(yj0+1 + yj0)x]|2т j 0=0
j
6 M12(|[yj+1]|2 + kyX +1]|2)т + M15 E (|[yj0]|2 + kyX0]|2)т + F(tj)■ j 0=1
(3.30)
Выбирая т таким образом, что для всех т 6 т 0 , т 0 = ^ MME , и обозначая через F(t j ) = M 16 (P j 0 =0 (|[^ j ' ]| 2 + ^ 1 2 + ^ j 2 2 )т + |[y 0 ]| 2 + k y ° ]| 2 ) , из (3-30) получим
j
| [y j+1 ] | 2 + k y X+1 ] | 2 6 M 17 Е | [y j ' ] | 2 + || y X 0 ] | 2 т + M 18 F(t j ).
j 0=1 v 2
(3.31)
Оценивая первое слагаемое в правой части (3.31) с помощью леммы 4 из [16, с. 171], из (3.28) с учетом (3.29), (3.30) получим априорную оценку
I[y j+1 ] | Wj(D ,l ) + XX k (y ’ ' +1 + У 2 ' ) х ]^ т j 0 =0
6 M (XX ( | [^ j 0 ] | 2 + , j ' 2 )т + | [ у 0 ] |2г^0,1)
V j 0 =0
(3.32)
где M — положительная постоянная, не зависящая от h и τ .
Из полученной априорной оценки следует
Теорема 1. Пусть выполнены условия (1.5). Тогда при ст = 0.5 существует такое т0, что если т 6 то, то для решения разностной задачи (3.9)-(3.10) справедлива априорная оценка jj
| [y j+1 ] | W 2i (0 ,i ) + X k (y j 0 +1 + y j 0 ) x ]| 2 т 6 M( X (W 0 ]| 2 + ^' 0 2) т + ^W(0 ,1 )
2 0 =0 0 =0
где M — положительная постоянная, не зависящая от h и τ .
Таким образом, доказана устойчивость решения разностной задачи (3.9)–(3.10) по
начальным данным и правой части в сеточной норме | [y 2+1 ] |
W 2 1 (0 ,l )
на слое.
Пусть u(x,t) — решение задачи (3.1)-(3.4), y j — решение разностной задачи (3.5)
(3.8). Обозначим через z = y — u погрешность. Подставляя y = z + u в (3.5)-(3.8) и
считая u(x, t) заданной функцией, получим задачу для z :
z t,i = X i (az $^ ) x,i + (Yz xt ) x,i + b + ^+14? + b - a iz5 — d -S^ + S, (3-33)
Nj h aiX0zX^0 + Yizxt,0 = X 4 z(" ~ + X тР8'zsN + 2 (zt’0 + d0z^ ) — V1, (3-34)
s=0 s =0
— (ayvXTVz X^)■ + YNZ x tN } = h (z t,N + dvS ’ } — V 2 , (3.35)
z(x, 0) = 0, (3.36)
ф г = O(h 2 + т 2 ) , V 1 = O(h 2 + т 2 ) , V 2 = O(h 2 + т 2 ) — погрешности аппроксимации на решении исходной задачи при каждом фиксированном t , в силу построения оператора Л при ст = 0.5 .
Применяя априорную оценку (3.32) к задаче для погрешности, при ст = 0.5 получаем оценку jj
I [z j+1 ] | 2 + k = X+1 ] | 2 + X II (z j ' +1 + z 0 ) , ] | 2 т 6 M X (| [® j ' ] | 2 + v j 0 2 + v 2 0 2) т, j 0 =0 j 0 =0
где M — положительная постоянная, не зависящая от h и τ .
Из полученной априорной оценки следует сходимость схемы (3.33)-(3.36) при ст = 0.5 со скоростью O(h 2 + т 2 ) на слое.
4. Априорная оценка решения задачи в многомерной области
В замкнутом цилиндре Q T = G х [0, T] , основанием которого является p -мерный прямоугольный параллелепипед G = {x = (x 1 ,...,x p ) : 0 6 x a 6 l a , a = 1, 2,...,p } с границей Г , G = G U Г рассматривается нелокальная краевая задача
∂u
(4 . 1)
■dt = Lu + f (x,t), (x,t) G Qt, lα в-а(x, t)u(x, t) dxa
(4.2)
+ У P - a (t, T )u(x i , . . . , x a - 1 , l a , X a +1 , . . . , X p , T) dT - ^ - a (x, t), X a = 0, 0
Па (x,t) = 0, xa = la,(4.3)
u(x, 0) = uo(x), x G G,(4.4)
где Lu = P a =1 L a u,
L a U = (k a (x,t)u xa)x a + (п « (х, t)U x a t)x a + Г а (x, t)U x a — q a (x,t)u,
Qt = G X [0 |^aI, |raI, Ш, |e—a(x,t)b |P—a(t,T)| 6 c2, na(x,t) = j 0 t na(x,t) = ka(x,t)uXa+ na(x,t)uxat — полный поток, 0 6 t 6 t, co, c1, c2— положительные постоянные, a = 1,p. Относительно коэффициентов задачи (4.1)–(4.4) предположим, что они обладают таким количеством непрерывных производных, которое необходимо для обеспечения нужной гладкости решения u(x, t) в цилиндре QT. Допуская существование решения дифференциальной задачи (4.1)–(4.4) в цилиндре QT , получим априорную оценку для ее решения, воспользовавшись методом энергетических неравенств. В дальнейшем изложении будем пользоваться скалярным произведением и нормой (u.v)=/uvdx, G (u,u) = kuk2, kuk0 = У u2dx, G p uX = EuXa , lα kukL2(0,la) = j u2(x,t) dxa. o Умножим уравнение (4.1) скалярно на u: p p pp + ( Era(x,t)uxa ,u) - ( E qa(x,t)u,u ) a=1 ^ ^a=1 Преобразуем интегралы, входящие в (4.6): (ut,u)=j utudx=2 ddt kuko, G + (f (x,t),u). p xα p ,u) = / 52 (kaUxa)xaudx ; JG a=1 pp = E / kauuxa |oa dx0 -E / ka C^xa) dx, a=1z^ a=1 Gα G (4.6) (4.7) (4.8) p xα p pl ,u) = / 52 (naUxat)xaudx = 52 / иПаUxa^o"dx / 1 =1 rv=1 " г a=1 a=1n G Gα pp + 2 X / nta (uxa fdx - — X / у (uxa )2dx. a=1g a=lg Далее для оценки слагаемых в правой части применим неравенство Коши с ε pp ( 52 Га (x,t)Uxa ,u) = / 52ra(x,t)Uxa udx a=1 g a=1 pp 6|2 X / CuXa )2 dx +S2 X / u2 dX, G G p pp -1 52 qa(x, t)u, u) = — 52 qa(x, t)u2 dx 6 c2 52 / u2 dx, a=1 ' g a=1 a=1 g I f(x,f),u I = / f (x,t)u G dx 6 2kfk0 + 2kuk0, (4.9) (4.10) (4.11) (4.12) где Ga = |x° = (x1, x2,..., xa-1,xa+1,..., xp) : 0 < xk < lk, k = 1, 2,... , a — 1, a + 1,..., p|, dx0 = dx1 dx2 ... dxa-1 dxa+1 ... dxp. Подставляя (4.7)–(4.12) в (4.6), получаем неравенство dd kuk0 + dd X / na(uxa )2 dx + X / ka (u^x:^ )2dx a=1G a=1G pl (4.13) 6 2 52J u(kaUxa + naUxat) ^dx p + 3 c2 X / (uxa) dx + (3pc2 + 1)kuk0 + kf k2. = g: Первое слагаемое в правой части (4.13), пользуясь теоремой 6.5 [13], краевыми условиями (4.2), (4.3) и неравенством Коши с ε, оценим так: pl 52 / u(kaUxa + naUx^Oa dx а=1 Gα p = X / (na(x,t)u(x,t)|xa =la — na(x,t)u(x,t)|xa =o) dx а=1 Gα lα — u(x,t)^ j в-а(x,t')u(x,t') dxa t + j P-а (t,T)u(xi, . . , xα- 1, la, xa+1, . . . , xp, T) dT - ^-a(x,t) dx0 xα=0 t M1(kukO + kuxkO) + M2 У (llullO + llux ll2)dT + 2 (4.14) Тогда из (4.13), с учетом (4.14), находим 4 kuk2 + 4 X / Па(иха )2 dx + dt dt α=1 G t µ2-αdx0. α=1 Gα >2 j ka(uXa)2dx 6 Мз (kuk =1 G dT + X j Ц—а dx + kf 112. α=1 Gα (4.15) Проинтегрировав (4.15) по τ от 0 до t, получаем t 6 M5 +M7( Z kuk2 + kuxk2 + kux k2,Qt tτ IUxkO)dT + Мб j j (kukO + kuxkO)dTidT 00 (4.16) Gα dT + ku0(x)k2 + ku0(x)k2j . Оценим второе слагаемое в правой части (4.16) следующим образом: tτ j J (kukO + kuxko) 00 dτ1 dτ 6 T J (kuk2 + kuxk2) dT- (4.17) С помощью (4.17) из (4.16) находим t kukO + kuxkO 6 M8 j (kukO + kuxkO) dT +М7 На основании леммы Гронуолла из (4.18) получаем неравенство t (kukO + kuxk2) dT (4.18) (4.19) Учитывая неравенство (4.17)–(4.19), из (4.16) получаем априорную оценку tp Hull W2 (G) + kuxk2,Qt 6M(tH^ (kf k2 + X j ^-adx\dT + kuo(x)kWi(G)) , V 0 V a=1Ga (4.20) где M — зависит только от входных данных задачи (4.1)–(4.4). Из априорной оценки (4.20) следует единственность решения исходной задачи (4.1)– (4.4), а также непрерывная зависимость решения задачи от входных данных на каждом временном слое в норме пространства W1(G).
5. Устойчивость и сходимость разностной схемы Для решения задачи (4.1)–(4.4) применим метод конечных разностей. В замкнутом цилиндре QT введем равномерную сетку [14]: ШhT — Шh X Шт — { (xi ,tj), x G ШЬ, t G Шт } , Ш h — П ... , ... . — {xaa — iaha, ia — 0, 1,.. .,Na, Na ha — la} , a=1 Шт— {tj — jT, j — 0,1,..., m, тт — T}. На сетке Шн,т дифференциальной задаче (4.1)-(4.4) поставим в соответствие разностную схему, порядка аппроксимации O(|h| + г): где Л(t) — ^Лa(t), 5(t) — ^6a(t), a=1 a=1 Лa(t)У(a) — (aa Уха) xa + Г+Уха + Г _ yi - yi-1 _ yi+1 - yi ' xa — ha ’ ^ — ha + + ra — ra + ra , |ra | — ra Г- — 0.5 (ra - |ra|) 6 0, ayxa - day, 5a (t)y(a) — (YayXat) xa , yj+1 - yj j - yt —----------, y — yj, y — yj+ , τ ' r-, r+ — 0.5(ra + |ra|) > 0, tj— jT, tj+ T — (j + 1)т, где т, h — шаги сетки, ia — 1,..., Na, aa — ka (x ,tj ), Ya — na (x ,tj ), da — qa (xi, t), ^i — f (xi, tj ), T(ia ) (T(i1) T(i2) ^(ia) T(ip) ^ xa ^a'^a, xi I x1 , x2 , . . . , xa , . . . , xp 1, x o5a — x1 ,...,xa-1,xa — 0.5 ha, xa+1,..., xp, xao) — 0, yao) — (x1 ,x2,... ,xao),... ,xp,T), yaNa) — (x1,x2,... ,xaNa),. ..,xp,T x (Na) a—a a—a. Для решения задачи (5.1)–(5.4) получим априорную оценку, воспользовавшись методом энергетических неравенств. В пространстве функций определим норму следующим образом: (u,u) = ||u||2, (u, u] = ku]|2, pp (u,v] = £(u,v]a, BY,]|2 = £ BY,.]|2. а=1 а=1 Умножим тогда разностное уравнение (5.1) скалярно на 2ту : 2т(у, у) = 2т(Л(t)У, у) + 2т(5(^у, у) + 2т(у, у). (5.5) Преобразуем суммы, входящие в (5.5), с учетом условий (5.2), (5.3) и формулы 2ууt = (У2)t+ т (yt)2: 2т (yt, у) = (1, у2) - (1, у2) + т2(1, у2), (5.6) pp (Л(t)У, у) + (5^)у, у) = ( X Ла(t)y, у ) + ( X 5а(t)y, у ха=1 ' ха=1 pp = X (Ла(t)y,y) + X (5а(^)у,у) а=1 а=1 (5.7) p = X ((^ )ха ,у) + (^аУXat)Xa , у) + (г+уХа , у) + (Г-уХа , у) — (^у,у)) . а=1 Применяя первую разностную формулу Грина в (5.7) и подставляя преобразованные таким образом выражения в (5.5), с учетом (5.6), получаем pp (1, у2) - (1, у2) + т2(1, у2) + т X (1 (YауХа)t ] а + т2 X (Yа, (УXat)2 ] а а=1 pp pp = -2тХ (аа,уХа ]а - тХ (Ytа ,уХа ]а + 2тХ (r+уха , у) + 2т X (Г-уХа , у) а=1 а=1 а=1 p p N p -2т X (dа, у2) - 2т X уа0)X в-а.у~ + 2т X ^-ауа°) а=1 а=1 s=0 pj -2тХуа0)Хр-а^-yаNа),s+1T + 2т(у,у). а=1 Оценим суммы, входящие в (5.8): pp X (аа ,уХа ]а > c1X (1,уХа ]а = c1 (1,уХ ] = С1кух]|2, а=1 p т2Х (Yа, (УХаt)2 ]а > т2col|yxt]|2, (5.10) а=1 pp X (r+уха ,у) + X (r-уХа ,у) 6 2c2 кух]| 1|у k 6 С2 (НуН2 + кух]|2), (5-11) а=1 а=1 pp - X(da,У2) 6 C2 Х(1,У2) = C2kyk2, (5.12) a=1 a=1 pN -E • \ e-a-sys~ 6 a=1 s=0 pN 2E (ya0)) + (Ee-a.-y.-~ a=1 L s=0 6 M1 0Ы|2+ kyk2), (5.13) pp p E ' ■ ■ 6 2 E ' . + (y™)2) 6 2(sIMf2 + a=1 a=1 a=1 pj - X ? VO .y(Na),s+1f<1 / vya 2_>p-a,s,j ya T 62 a=1 s=0 pj e (e a=1 ^ s=0 a (Na),s+1f V, ( (0) )2A p-a,s,j ya T J + ^ya ) ) 1j 62(ekyx]I2+ c(£)kyk2) + ME (ekyx+1]|2 + с(£)Ну+1II2)T, s=0 (5.15) 4.y) 6 2kyk2+ 2kll2. (5.16) Учитывая оценки (5.9)–(5.16), после несложных преобразований из (5.8) находим: ЛУЛ2- ЛуЛ2 + C0kyx]|2- C0kyx]|2+ T2kyt]|2+ t2C0ky-t]I2+ 2TC1 kyx]|2 6 M3(kyk2+ kyx]|2)t + M4X (ky*+1Л2+ ЛуХ+1]|2)тт + m5(Л^Л2+ X^2a)t. s=0 a=1 (5.17) Просуммируем (5.17) по j 0 от 0 до j : j llyj+1||2 -u ||7,j+1l|2 E ( j0+ 0+11I2t ji+ 0+11I2t 4- j0+ 0+1ll2V лу II + Лух ]| + / v I kyt ]| T + Лухt ]| T + Лух ]| )T j0 =0 j j j0 6 M« E («у2 '+1л2 + луХ'+1]2) t + M7 E E («ys"1»2 + j '=0 j'=0s=0 »уХ+1]|2) tt (5.18) jp +M8E(kyj'k2+ Ey2-a)T + лу0л2+kyX]|2 j'=0 a=1 Оценим второе слагаемое в правой части (5.18) jj0 j E E (kys+1k2+ ЛуХ+1]|2)TT 6 T E (kyj'+1Л2+ ЛуХ'+1]|2)T. (5.19) j '=0s=0 j'=0 В силу (5.19) из (5.18) имеем j kyj+1k2 + i'4 '] 2 + X (kyt'+1]|2T + Ц4t+1]|2T + kyX'+1]|2)т j '=0 j 6 Ms X (kyj'+1k2+ kyX'+1]|2)T j '=0 +M8 ( X (k4'k2+ X j) + ks0k2+ kyX]|2) (5.20) j '=0 a=1 j = M»(kyj'+1k2 + kyX'+1]|2)T + M9 Ё (kyj112 + Ы'] |2)T j '=1 +M1o(X (kjk2+ X ja)t + y k2+ kyX]|2). j'=0 a=1 2 Выбирая t таким образом, что для всех т 6 tq, T0 = 2MM9, из (5.20) получим j ИХ1!!2+ kyX+1]|26 M11 Е (kyj'k2+ kyX']|2)T j '=1 (5.21) + M1«( X (k-Zk2+ Xj„2)т + ky0k2+ kyX]|2" j =0 a=1 Оценивая первое слагаемое в правой части (5.21) с помощью леммы Гронуолла для сеточной функций [17], из (5.18) с учетом (5.19), (5.20) получим априорную оценку j j+1||2 -U ||7/j+1]|2 4- X f W '+11I2T 4- jl+ '+11I2T 4- j°+ '+11I2V ky II + kyx ]| + / v I kyt ]| T + kyxt ]| T + kyX ]| )T j =0 j (5.22) jp 6 M E (k^j'k2+ E У-'a2)T + ky0k2+ kyX]|2). j =0 a=1 Тогда справедлива следующая Теорема 2. Пусть выполнены условия (4.5). Тогда существует такое т0, что если т 6 Та, для решения разностной задачи (5.1)-(5.4) справедлива априорная оценка Иу,+11&№) + XX (kyX'+1]|2т + kyXX+^^T + kyX'+1]|2)т j '=0 jp 6 M E (k^j' k2+ E ^—'a') T + ky"kW3(G) j =0 a=1 где M — положительная постоянная, не зависящая от |h| и τ . Пусть u(x, t) — решение задачи (4.1)-(4.4), y(xi, tj) = yj — решение разностной задачи (5.1)-(5.4). Обозначим через zj = yj — uj погрешность. Тогда, подставляя y = z + u в (5.1)–(5.4), получим задачу для z: zt = A(t)z + 5(t)z + Ф, (x,t) E WhT, (5.23) Nj a-+1a)Zxa + Y—+1a)Zxat = X e-a,sZs~ + X P-a,s,jzNa)T - v—a, xa = 0, (5.24) s=0 s=0 — v+a, xa — la, (5.25) a+aZxa + Y+aZ$a t z(x, 0) = 0, x E Dh, (5.26) где Ф = O\\h\ + t), v-a= O\\h\ + t), v+a= O(\h\ + t) — погрешности аппроксимации на решении задачи (4.1)–(4.4). Применяя априорную оценку (5.24) к решению задачи (5.23)–(5.26), получим оценку j IjllWj(G) + X (Н'II2T + НгАФ + H'+1]|2)T j0 =0 jp 6 m x (n»j' k2+X(v-a2+j2)) t, j'=0 a=1 где M — положительная постоянная, не зависящая от |h| и τ . Из полученной априорной оценки следует сходимость схемы (5.23)–(5.26) со скоростью O(\h\ + t) в сеточной норме W21(G). Замечание. Полученные результаты имеют место и в случае, когда уравнение имеет вид: Ut = (k(x, t)ux)x + (n(x, t)ux)xt + r(x, t)ux - q(x, t)u + f (x, t), 0 < x < l, 0 < t 6 T, если условия (1.5) дополнить условием п E C3,2(Qt)•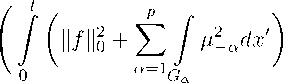
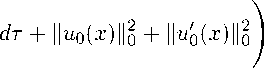
yt — Л(t)y + 5(t)y + y,
Nj
(x, t) G Xhr,
(5.1)
a-+a1a)yxa + Y-+1a)yxat — X e-a,sys~ + X
s=0 s=0
P-a,s,jyONa)T - ^-a, xa — 0,
(5.2)
- (a+ayxa + Y+ayxat) =
0, xa — la,
(5.3)
y(x, 0) — uo(x),
x G Шh,
(5.4)
pp
Список литературы Априорные оценки решения нелокальных краевых задач для псевдопараболического уравнения
- Баренблат Г. И., Желтов Ю. П., Кочина И. Н. Об основных представлениях теории фильтрации однородных жидкостей в трещиноватых породах//Прикладная математика и механика.-1960.-Т. 25, вып. 5.-C. 852-864.
- Дзекцер Е. С. Уравнения движения подземных вод со свободной поверхностью в многослойных средах//Докл. АН СССР.-1975.-Т.~220, \No 3.-C. 540-543.
- Рубинштейн Л. И. К вопросу о процессе распространения тепла в гетерогенных средах//Изв. АН СССР. Сер. геогр.-1948.-Т. 12, \No 1.-C. 27-45.
- Ting T., Cooling A. Process according to two temperature theory of heat conduction//J. Math. Anal. Appl.-1974.-Т. 45, \No 9.-P. 23-31.
- Hallaire M. L'eau et la production vegetable//Institut National de la Recherche Agronomique.-1964.-\No 9.
- Чудновский А. Ф. Теплофизика почв.-М.: Наука, 1976.-352 с.
- Colton D. L. Pseudoparabolic equations in one space variable//J. Dif. Eq.-1972.-Vol. 12.-P. 559-565.
- Ахиев С. С., Гусейнов О. М. О фундаментальном решении одной краевой задачи для гиперболического уравнения третьего порядка.-Баку: Азерб. ун-т, 1983.-9 с.
- Водахова В. А. Краевая задача с нелокальным условием А.М. Нахушева для одного псевдопараболического уравнения влагопереноса//Диф. уравнения.-1982.-Т. 18, \No 2.-С. 280-285.
- Кожанов А. И. Об одной нелокальной краевой задаче с переменными коэффициентами для уравнений теплопроводности и Аллера//Диф. уравнения.-2004.-Т. 40, \No 6.-С. 763-774.
- Шхануков М. X. О некоторых краевых задачах для уравнения третьего порядка, возникающих при моделировании фильтрации жидкости в пористых средах//Диф. уравнения.-1982.-Т. 18, \No 4.-С. 689-699.
- Чудновский А. Ф. Некоторые коррективы в постановке и решении задач тепло-и влагопереноса в почве//Сб. тр. по агрофизике.-1969.-Вып. 23.-C. 41-54.
- Ладыженская О. А. Краевые задачи математической физики.-М.: Наука, 1973.-407 с.
- Самарский А. А. Теория разностных схем.-М.: Наука, 1983.-616 c.
- Андреев В. Б. О сходимости разностных схем, аппроксимирующих вторую и третью краевые задачи для эллиптических уравнений//Журн. вычисл. матем. и матем. физ.-1968.-Т. 8, \No 6.-С. 1218-1231.
- Самарский А. А., Гулин А. В. Устойчивость разностных схем.-М.: Наука, 1973.-416 c.
- Самарский А. А. Однородные разностные схемы на неравномерных сетках для уравнений параболического типа//Журн. вычисл. матем. и матем. физ.-1963.-Т. 3, \No 2.-С. 266-298.


