ARIMA-модель пульсового сигнала

В течение многих лет, восточная медицина доказывала высокую эффективность в лечении различных хронических заболеваний. Наиболее перспективной областью в восточной биометрии считается математический анализ пульсового сигнала (сфигмограммы), как главного источника информации о функциональном состоянии организма человека [1].

Анализ и моделирование пульсового сигнала позволяет получить множество информативных параметров, интерпретируемых с точки зрения восточной медицины.

Рассмотренны известные попытки математического моделирования пульсовой волны такие как метод сплайн-аппроксимации, основанный на применении интерполирующих сплайнов разных порядков – кубических и локальных B-сплайнов, модель Акулова, представляющая собой произведение экспоненциальной и тригонометрической функции с тремя параметрами, модель Самарского, основанная на законе сохранения энергии и импульса и др. Каждая из этих моделей и подходов имеют свои достоинства и недостатки, и все же остаются далеко не совершенными в виду сложности данного биофизического явления в организме человека [2].

Одним из перспективных подходов статистического моделирования пульсового сигнала, представленного в виде временного ряда, является применение методологии Бокс-Дженкинса (ARIMA-модель авторегрессии и проинтегрированного скользящего среднего) [3, 4, 5].

Математическое описание

Временной (динамический) ряд – последовательность наблюдений некоторого признака X в последовательные моменты t . Отдельные наблюдения называются уровнями ряда и обозначаются x t , t=1,..., n .

ARIMA-модель представляет собой синтез двух различных методов моделирования временного ряда: скользящего среднего и авторегрессии [3].

Модель скользящего среднего q -го порядка MA(q) временного ряда X t имеет вид:

q

X, = у b ? + .

t             j t—j       t j=1

где ε t – белый шум, b j – параметры модели. Модель содержит q+1 параметров ( b 1 , b 2 , …, b q , и σ² ), значения которых оценивается по принципу максимального правдоподобия.

Модель авторегрессии p-го порядка AR(p) временного ряда X t имеет несколько иной вид:

p

• X, = c + У aX ,.+ et                    (2)

t        it —it                  v / i=1

где ε t – белый шум, a i – параметры модели, c – константа. Модель содержит p+1 параметров ( a 1 , a 2 , …, a p , и σ² ), значения которых, как правило, оценивается по методу наименьших квадратов.

Итак, объединенив две вышеуказанные модели получаем модель авторегрессии и скользящего среднего порядка (p, q) - ARMA(p, q) :

pq

Xt = c + У aXt i + У b i^st i + ^              (3)

t                      i t—i              j t—j t i=1                j=1

которая содержит p+q+1 параметров.

В случае если наблюдаемый ряд X t имеет признаки нестационарности (например, какие-либо детерминированные тренды – полиномиальный, линейный и т.д.), то модель не может является адекватной. Тем не менее в этом случае, некоторая разность наблюдаемого процесса порядка d , может оказаться стационарной: Δ ^d X t , где Δ оператор разности, Δ X=X t -X t-1 – разность первого порядка (аналог дифференцирования), Δ ^d – последовательное взятие первой разности d раз. Теперь для описания полученного процесса Δ ^d X t уже можно эффективно применить ARMA – модель. В итоге, получили модель авторегрессии и проинтегрированного скользящего среднего порядка. При этом p – параметр AR -части, d – степень интеграции, q – это параметр MA -части. ARIMA(p, d, q) (от английского — «Auto-Regressive Integrated Moving Average» ):

pq

A X = c + ^ ajXf i + ^\bi^t i + ^(4)

t                      i t—i              j t—jt i =1

Алгоритм построения

I этап. Идентификация параметров.

• 1.    Установить порядок разности интеграции d , то есть добиться стационарности ряда, взяв достаточное количество последовательных разностей (X t =X t - X t-1 ) . Порядок d устанавливается исходя из поведения автокорреляционной функции ряда.

• 2.    К полученному стационарному ряду Y t , подбираем ARMA(p,q) . Исходя из поведения автокорреляционной и частной автокорреляционной функции, устанавливаем параметры p и q . Если ряд имеет сезонную составляющую с определенным периодом, в модель необходимо внести сезонную корректировку. Сезонные модели ARIMA являются обобщением обычных моделей ARIMA. Полная сезонная модель может быть представлена в виде ARIMA(p, d, q)(Ps, Ds, Qs) где к параметрам модели добавлены сезонные параметры: сезонный параметр авторегрессии – Ps , сезонная разность – Ds , сезонный параметр скользящего среднего – Qs.

II этап. Оценивание параметров.

С помощью специальных численных процедур по известным данным на данном этапе оцениваются коэффициенты a 1 , a 2 , …, a p , b 1 , b 2 , …, b q и σ² при условии, что мы уж знаем p и q . Оценка значений параметров проводится на основе метода наименьших квадратов и принципа максимального правдоподобия.

• III    этап. Проверка адекватности модели.

Исходной информацией для анализа адекватности модели служат остатки (в данном случае остаточные ошибки – это предполагаемые значения ε t ). Проверяем качество модели при помощи критерия AIC. Мы предполагали, что ε t является белым шумом, поэтому, проверяем некоррелированность остатков.

Кроме того существуют более формализованные критерии, например, критерий предложенный Акаике AIC для модели ARMA(p,q) выглядит следующим образом:

AIC ( p , q ) = In a ² + 2

p + q

T

₂ _ RSS

°  T - p - q где T – число наблюдений, RSS – остаточная сумма квадратов.

Выбор подкласса моделей производится на основе сравнение показателей качества с различными значениями параметров p и q.

• IV    этап

Практическое применение модели. Анализ различных путей модификации модели, в том числе необходимости предобработки исходного сигнала.

Модель пульсового сигнала

Для реализации данного подхода на эмпирических данных выбран реальный пульсовой сигнал человека, полученного с помощью специального аппаратно-программного комплекса (рис.1.).

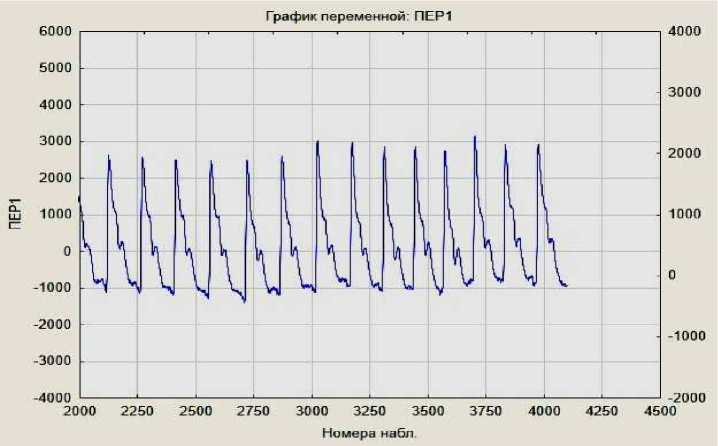
Рис. 1. График сфигмограммы пульсовой сигнала

Идентификация и оценка параметров модели производится с применением программного пакета STATISTICA 10. С помощью модуля «Time Series Analysis» производится оценка параметров модели по принципу максимального правдоподобия, качественный и количественный анализ автокорреляционных и частных автокорреляционных функций, анализ остатков, критериальная и визуально-графическая оценка адекватности модели, а также прогнозирование. В результате проведенных расчетов и экспериментов в рамках методологии получено три класса моделей реальной пульсовой волны, отвечающих требованиям адекватности(Табл. 1).

Таблица 1.

Классы моделей и их характеристики качества

№	Модель	AIC	W	RSS
1	ARIMA(2, 1, 0)(1, 1, 0)	8,0334239058	0,87201	12165760
2	ARIMA(1, 1, 0)(1, 1, 0)	8,1158696188	0,86185	13211282
3	ARIMA(2, 0, 0)(1, 1, 0)	8,1996723144	0,87821	14639777

Исходя из количественных характеристик, анализа остатков (в т.ч. остаточной коррелограммы) и полученного прогноза определена модель под №1 с лагом 146 как наиболее адекватная среди рассматриваемых.

Итак, выбранная модель ARIMA (2, 1, 0)(1, 1, 0) с оцененными параметрами приобретает следующую аналитическую форму:

A ¹ X. = c + 1,33699646176872 ( a ¹ X_{t - 1} ) - 0,5328006151115 ( a ¹ X _t _ ₂ ) -

- 0,525157536913316 ( a ¹ (146) X_{t - 2} ) + s _t

AIC ( 2,0 ) = in ^12165760 + 2 2 = 8,0334239058 ^{v 1}     9353 - 2    3953

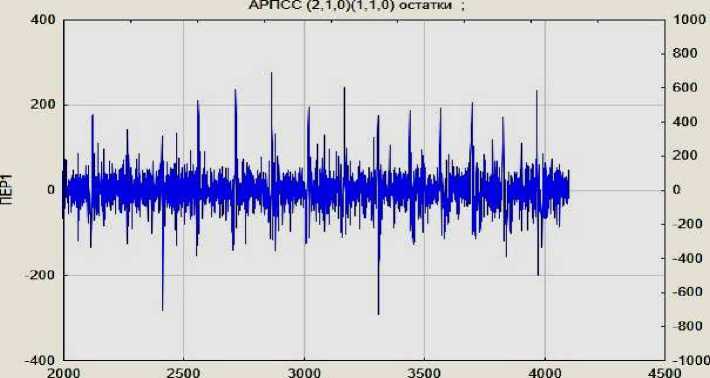
Графики остатков и остаточной автокорреляционной функции приведены ниже (рис. 2, 3).

График переменной: ПЕР1

Номера набл

Рис. 2. График остатков ARIMA (2, 1, 0)(1, 1, 0)

Автокорреляцион. функция

ПЕР1 : АРПСС (2,1.0)(1,1,0) остатки ; (Стандартные ошибки - оценки белого шума)

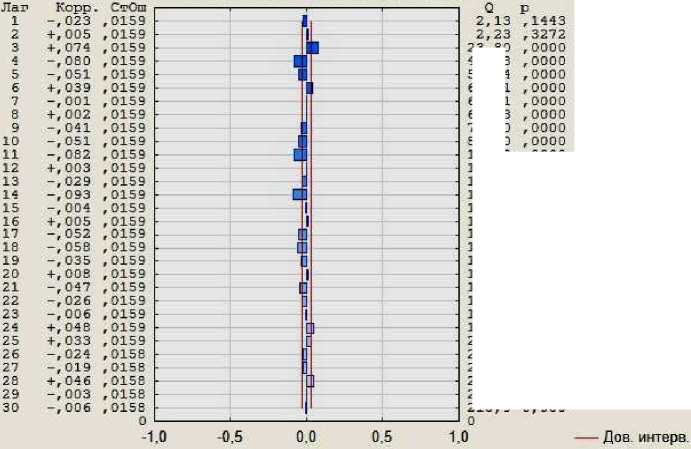
Рис. 3. Коррелограмма остатков ARIMA (2, 1, 0)(1, 1, 0)

23, ВО

49, за

59,54

65, 61

65, 61

65, 63

72,30

82, 60

109, 3

109,3

112, 6

146,7

146, В

146, 9

157, 9

171,3

176,1

176, 4

185,1

187,8

183,0

197,2

201, 6

203, 9

205, 4

213,7

213,7

213, 9

,0000 ,0000 ,0000 О, ООО 0,000 О, ООО О, ООО 0,000 О, ООО О, ООО О, ООО О, ООО О, ООО О, ООО О, ООО О, ООО О, ООО О, ООО 0,000 О, ООО

На основе полученной модели построен прогноз на два сердечных цикла пульсового сигнала (рис. 4). График прогноза считаем вполне удовлетворительным.

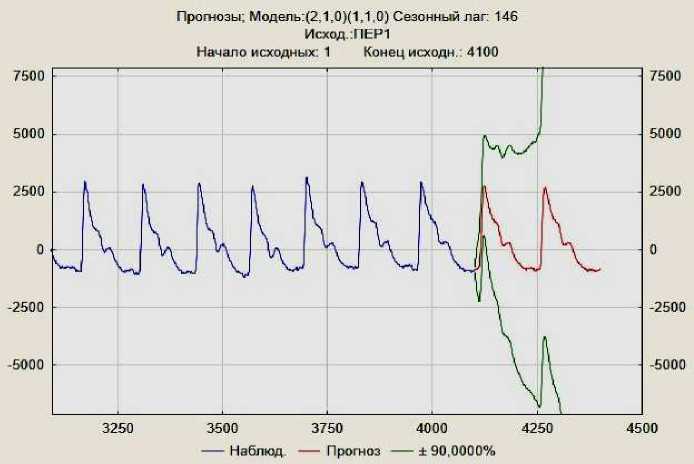
Рис. 5. Прогноз ARIMA (2, 1, 0)(1, 1, 0)

Заключение

Таким образом, в данной работе мы применили методологию Бокс-Дженкинса для моделирования дискретного пульсового сигнала человека. Построены адекватные модели ARIMA с применением пакета STATISTICA 10. Получен прогноз на несколько реализаций сердечного цикла.

Дальнейшее логическое продолжение исследования носит экспериментальный характер. Необходимо выявление взаимосвязей полученных параметров с различными физиологическими состояниями и типологическими особенностями организма человека.