Artificial neural estimator and controller for Field Oriented Control of three-phase I.M.

Published Online June 2019 in MECS

Variable Voltage Variable Frequency (VVVF) controllers of an induction motor are by a long way the most famous technique, because of its simplicity, and these forms of machines are widely used in many applications. Usually, the Volt/Hz is managed via D.C-A.C pulse width modulation inverter to maintain the airgap flux at its rated value and approximately constant, this form of manage known as "scalar control". In spite of scalar manipulate is really simple, but the inherent coupling effect for both torque and flux are capabilities of voltage or current and frequency (i.e. throughout Volt/Hz variation each torque and flux be various too), which gives sluggish performance and it may be unstable because of excessive order system effect [1].

The vector or field-oriented controller presents a perfect solution of this problem, which invented at the 1970s, the demonstration that; an induction motor can be treated likes separately excited D.C. motor, delivered a renaissance within the high performance of A.C. Drives, vector controller is likewise known as decoupling, orthogonal, or trans-vector manage. The principle of this technique is to rotate the direct axis continually with the identical direction of the rotor pole axis, or with the aid of aligned the rotor flux vector ( ) at the d-axis. This may be executed with the aid of estimating the exact unit vector (cos 0e and sin 0e ). In this way, it's required to estimate the flux vector ( ) and the unit vector by using complicated digital signal processing (DSP) and microcontroller analysis [1,2].

Recently, the Artificial Neural Intelligence (ANI) has penetrated widely in engineering sciences and their applications, which appears very promising and effective tool with advanced features. In the literature, there are great efforts to implement intelligent neural networks in the estimator domain to reduce complexity and improve performance. But we don’t find in the literature any attempts to combine between the use of neural networks in both of the controller and the estimator.

In this paper, the features of the ANN are exploited to estimate the flux vector ( ), unit vector (cos 0_e and sin0_e), and the electromagnetic torque T _e instead of using the complicated microprocessor DSP systems. As well as, implement the artificial neural controller instead of conventional Proportional Integral (PI) controller. Therefore, the main contribution to this paper is concentrated in combining between the artificial neural controller rather than the traditional PI control in addition to the neural estimator, which was not previously used or proposed in the literature.

The related works and recent contributions of this area are presented briefly in the next section to realize the significant of this work. The mathematical representation of the induction motor and the concepts of vector control theory are illustrated in the later sections. Next, the implementation of the proposed neural estimator and controller and simulation results are presented in the rest of this paper.

• II.    Related Works Survey

In the last decade, as mentioned before, efforts have been made and are still being made to use intelligent systems such as fuzzy, neural, neurofuzzy ...etc., alone or combined with optimization methods, of representing the estimator in the vector and field oriented control systems, because of their great impact in reducing the complexity of the system and improve performance significantly. The most important contributions in this area can be summed up briefly in the following:

Y. Song, et al , 2010 [3], proposed a novel linearization and decoupling method by using artificial neural network (ANN) to overcome the effect of parameters variation during operation of induction motor, the decoupling and linearization implemented by field oriented control and analytical inverse control is presented. The results show that the proposed scheme has excellent dynamic and static control performance.

Peter Girovský, et al , 2010 [4], deal with a problem of speed estimation in a shaft sensorless field oriented control structure with induction motor that is based on neural modeling approach. Two different neural estimators were developed; one for observing the magnetic flux and the other one for observing motor angular speed.

Fabio Lima, et al , 2010 [5], proposed the development of an adaptive neurofuzzy inference system (ANFIS) angular rotor speed estimator applied to a FOC sensorless drive. Simulations to evaluate the performance of the estimator considering the volts per hertz and vector drive system were realized using the Matlab/Simulink.

Chitra Venugopal, 2010 [6], presented a novel Adaptive Neural Fuzzy Inference System (ANFIS) based matrix converter for speed control of induction motor. The reference voltage is used to generate the duty cycle for matrix converter switches. The matrix converter is designed using Venturini algorithm and results are shown under different switching frequencies.

Arif Iqbal and M. Rizwan Khan, 2010 [7], presented a new model reference adaptive system (MRAS) speed observer for high-performance field oriented control induction motor drives using neural networks. Performance analysis of speed estimator with the change in motor parameters especially resistances of stator and rotor is presented. The estimator was designed and simulated in Matlab/Simulink. Simulation result shows a good performance of speed estimator especially under fault condition.

Md. Abdur Rafiq, et al , 2012 [8], proposed an Artificial Neural Network (ANN) as a speed tracker for induction motor drive. The effectiveness of the controller is tested for the tracking property using different types of reference speed. A sensorless scheme is proposed to overcome the disadvantages of rotor position sensors. Results show that the proposed controller provides accurate speed tracking characteristics.

Shoeb Hussain and Mohammad Abid Bazaz, 2014 [9], implemented an Artificial Neural-Fuzzy Inference System (ANFIS) for vector controlled induction motor. The efficiency of the system is also improved using an optimization algorithm wherein the rotor flux weakening is done as the system stability is reached. Simulation of a 5 Hp, 460 V, 50 Hz induction motor is presented and speed tracking is achieved under different operating conditions.

Hao Zhang, et al , 2014 [10], presented a new rotor flux estimation algorithm using neural network for induction motors, based on the left-inversion method. Using the fifth order model of the three-phase induction machines in a stationary two axes reference frame, a rotor flux “assumed inherent sensor” is constructed and its left-invertible is validated. The performance of the proposed algorithm is tested through simulation, proving the driven system has good behavior both in transient and steadystate operating conditions.

F. Lftisi, et al , 2016 [11], presented an intelligent indirect field oriented control (IFOC) technique for saturated induction motor (IM) drives in order to achieve high dynamic performance and wide operating range. A novel neural network map (NNM) is developed to find input weights of the neurons; without the need for any recurrent training process. A relative comparison between the PI controller and the proposed NNM based ANN controller indicates that the ANN mapping controller yields superior performance.

Md. Rifat Hazari, et al , 2016 [12], presented the ANN based speed control scheme of IM with considering Core Loss (CL) and Stray Load Loss (SLL). Simulation analyses are performed for both transient and steady state conditions. The results show the overshoot can be minimized by using the proposed control scheme. The simulations have been carried out by using Matlab/Simulink environment.

Son T. Nguyen, et al , 2017 [13], presented a method of the online speed estimation for three-phase induction motor in indirect field oriented control scheme accompanying an artificial neural network. The simulation results obtained using Matlab/ Simulink show that the estimated motor speed tracks the actual speed with very small error.

Ramin Nahavandi, et al , 2018 [14], proposed a robust modified FOC scheme based on artificial neural network (ANN) for speed control of IM, with regard to improve the system performance as well as ensure the stability, robustness and fast dynamic response. The estimation based on ANN to compensate for uncertain parameters in the motor’s dynamic model. Moreover, this estimation leads to lack use of flux and speed sensor, therefore, the method is cost effective The results show that the performance of system is independent of system uncertainty of parameters and variation load and presents the faster dynamic behavior.

• III.    Mathematical Representation of the I.M.

The mathematical modeling of the induction motor can appear as a transformer with rotating secondary winding, wherein the coupling parameters among the stator and rotor stages exchange constantly with the change of rotor position [1,2]. The motor model can be described by means of differential equations with time various mutual inductances, but such version has a tendency to be very complex.

Therefore, axis transformation is carried out to transfer the 3-phase parameters (flux, voltage, and current) to two-axis framework referred to as the dq-axis stationary framework or park transformation. Park transformation is implemented to refer the stator variables to a synchronously rotating reference frame fixed in the rotor, in which all parameters will appear as DC quantities.

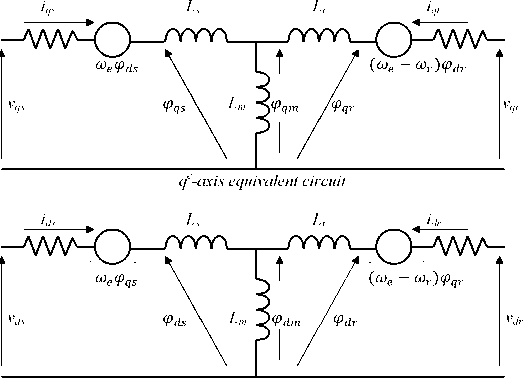
cf-axis equivalent circuit

Fig.1. The equivalent circuit of the 3-phase I.M.

The per-phase equivalent circuit of a three-phase induction motor is shown in Fig.1. From which the subsequent equations may be written [1]:

• •    Stator equations:

=     +(1)

=     +(2)

• •    Rotor equations:

=       +      (      )

=       +      (      )

Where: the superscript notation " e " referred to the synchronously rotating reference frame parameters. As known in the squirrel cage type induction motor V qdr =0, then the previous equation can be rewritten:

=   -     -(5)

=   -     +(6)

=-     -(     )

=-     +(     )

The produced torque through the interplay of airgap flux and rotor current may be discovered as:

=(3/2)( /2)⃑⃑⃑⃑⃑⃑  ⃑⃑⃑(9)

By resolving the variables into d ^e -q ^e components:

=(3/2)( /2)(     -     )(10)

The rotor dynamic equation:

=   +( )(11)

Where:  r = is the angular speed; P= poles number; J= moment inertia; TL= applied torque.

The current of the stator may be determined with the aid of:

=(12)

=(13)

The airgap flux:

=       +(14)

=       +(15)

Where:

=(16)

VL-nx^" Ls^" LT)

• IV.    Vector Control Technique

Vector or Field-Oriented Control permits a squirrelcage I.M. to drives with superior dynamic performance. It modulates the dynamic construction of an A.C machine into that of separately excited D.C machine [15]. In D.C machine, the magnetic flux is proportional to the excitation current, if the magnetic assumed to be fixing and unbiased of armature current, the armature current affords direct torque control, then:

∝ ∗ (17)

The FOC approach decouples the two additives of stator current; one imparting the airgap flux, and the other developing the torque. These current components provide impartial manage of flux and torque and the feature is linear [2,15]. These components are transferred again to the stator framework prior than feeding returned to the rotor. These two components are d-axis analogues to field current If, and q-axis is analogues to armature current Ia of the separately excited D.C motor. This strategy may be carried out by means of aligning the rotor field vector alongside the d-axis of the stationary framework as shown with the aid of the phasor diagram in Fig.2.

The basics of vector manage implementation may be depicted by the block diagram in Fig.3, wherein the motor version is represented in a synchronously rotating reference frame. The voltage-fed inverter produces three-phase voltages ( v_a, v_b, v_c ) in line with the reference command voltages ( v^, v _b, v^ ). The flux and torque components of stator current (i S _S) and (i^) is used as a control references to the machine, which can be inversely transformed to 3-phase reference currents ( i„, i_b, i C ), and then transferred to three phases voltage command ( v a, v_b, V c ) through (PI) controller [16]. The vector manage can be carried out by using either direct or indirect techniques, these methods are specific basically by how the unit vector (cos0_e and sin0_e) is evaluated.

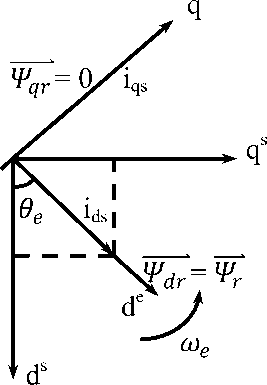
Fig.2. Concept of rotor flux orientation

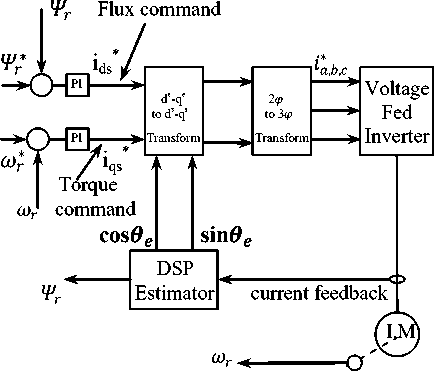
Fig.3. Block diagram of field oriented vector control

• V.    Field Vector Estimating

There are typically two strategies of flux estimating;

voltage and current templates. The voltage model has strong overall performance in high-speed applications but no longer in low speeds. Whilst, the current model has a universal overall performance in both low and high speeds [1]. The current version relies upon on the rotor equations within the axes stationary frame d ^s -q ^s , the superscript " s " noted to stationary framework quantities:

R Г iqr +^^4^ = 0(18)

Rridr + ^ + wr^r = 0(19)

Adding  (LmRr/Lr') ids  and  (LmRr/Lr^) iqsand simplifying:

= л m i ^+^-5 ](20)

=л m i^-^r^r-^](21)

The rotor flux is represented in (20 & 21) as a function of stator currents and speed. Therefore, understanding these alerts, the rotor flux and corresponding unit vector (cos 6_e and sin 6_e ) may be predicted by using DSP microprocessor to put into effect the subsequent equations [1, 17]:

Ill's ²      H'S ²

*r J * q r ⁺ * d r

Vqsr = i^ S i Tl 6e v^T = ^ir c OS eee

UJS s in 6e = -==-'ir coS 6e = S              (22)

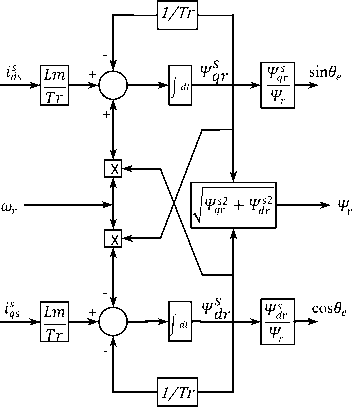
Fig.4. Current model flux estimation

Flux estimation via the current version needs for a speed encoder, but the benefit is that the driving operation may be extended down to low and zero speed. It's crucial to mention, that the inputs to the estimator ( ^•qs and ids ) have to be filtered by using a low bypass filter. The simulation of the current version estimator is depicted in Fig.4.

• VI.    Artificial Neural Estimator

Recently, we've seen big researches and trends attempt to apply the intelligent device in lots of engineering applications, due to its robust features likable to learn, fast adapting, inherent approximation functionality, and excessive degree of tolerance [18,19]. Neural Network Controller (NNC) became efficiently delivered to improve the performance of nonlinearity, which might be an effective tool used to improve the overall performance for both identification and controlling device. The global approximation capabilities of multi-layer perceptron make it a famous desire for modeling nonlinear structures and for imposing robust controllers. A neural network is a sensible gadget which can be learned or trained the use of real present inputs and outputs table, the process can be executed in real-time or off-time operation [18,19].

Thus, those features can be employed in this work to estimate the value of the rotor flux vector ^{⃑⃑⃑⃑⃑} and the unit vector (cos 6_e and sin 6_e ) as opposed to using DSP microprocessor, which lessen the complexity of the hardware, and decreases the Electro Magnetic Interference EMI effect on the microprocessor performance. Also, a neural-based PI controller may be implemented rather than the conventional PI controller.

• VII.    The Artificial Neural Estimator

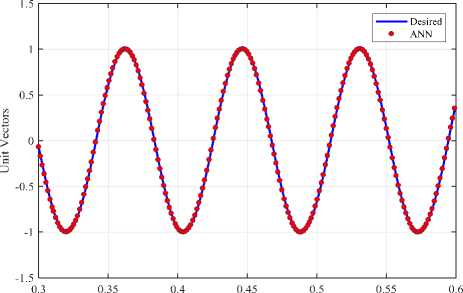
An ANN has four input and output neurons, ( iqs , i^_s , ^qr , ^dr ) and (cos 6_e , sin 6_e , T_e , ) respectively, including 7 hidden layers are designed and trained to meet the required performance of the estimator. It's crucial to mention right here that is, usually a huge wide variety of input and output records of different operating conditions should be used to train the neural network, but in this paper a unique unit step signal with rising and fall edges was used to training the network, which offers a top-notch overall performance in various speed situations. The overall accuracy performance of the neural network can be shown in Fig.5.

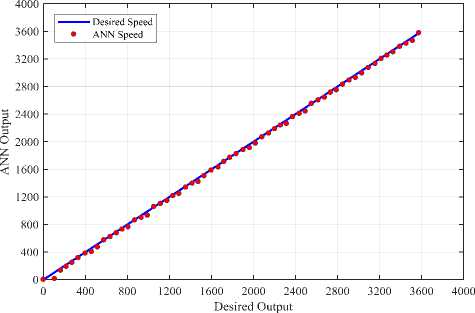
Fig.5-a. Accuracy performance for the neural controller

Time (s)

Fig.5-b. Accuracy performance of the unit vector estimation

• VIII.    Neural-based PID Controller

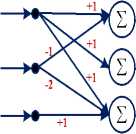
The disadvantage of the PID controller isn't appropriate for controlling a high time constant and nonlinear system, wherein the tuning of the P, I and D gains are complicated. With the improvement of contemporary computer technology, controlling techniques such as fuzzy and neural networks are developed. The adaptive PID controller neural network is a traditional PID approach combined with ANN, based on the discrete representation illustrated by [20,21], by which a new concept and new tool for controlling technique are presented. The self-learning ability of Back Propagation (BP) neural network can be tuning automatically and modifies the strong PID parameters. The PID controller combining BP neural network can give excellent consequences. Fig.6 shows the block diagram of the PID controller based on the discrete representation [22].

e(k)

e(k-1)

e(k-2)

∑

∑

∑

W i

W 2

W 3

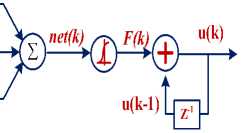
Fig.6. The PID-NN controller

The proposed adaptive controller law based on neural community method is as the following:

net(k) = ИИ1[е(/с) - e(k - 1)] + И2e(/c) + W3 [e(fc) - 2e(k - 1) + e(k - 2)](23)

Where, (k),(k-1) and e(k—2) are the error vectors of the k^th instance. W ₁ , W ₂ , W ₃ are the controller weights. The output activation function “ F ” is a tan-sigmoid function:

F (^=^^-1(24)

The controller drive signal:

(k) = (k - 1) + F(k)(25)

Despite the BP is managing powerful computation tool that has been used considerably within the regions of locating the excellent parameters (weights). But, it has a drawback of prolonged training process to meet the required performance of the controller. To speed up the convergent process and to protect the weights being restricted into local optima, the Particle Swarm Optimization (PSO) technique can be followed to assess the PID-NN controller weights [21,22].

Nowadays, the PSO technique is very popular optimization method used to find the optimal parameters instead of complex analytic processes. In this paper the PI-NN controller is required to control both of the torque and speed loops, thus, only W1 and W2 are found out by the particle swarm optimizing process. Fig.7 shows the searching progress for optimum values of W1 and W2 while the derivative weight W3 is set to zero. There are several fitness criteria used in the optimization process, in this work the Integral Time Square Error (ITSE) is used as a fitness function which is must be minimized in the optimization loop.

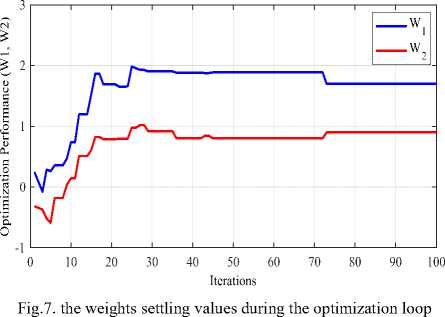
• IX. Simulation Results

The overall systems, both of the DSP and ANN-based estimator and controller, are simulated by using MATLAB-SIMULINK program as shown in Fig.8. The neural estimator weights were trained by using the BP technique to meet a set of input-output recorded table for different operating conditions (different loads and speeds). Whereas, the optimum weights of the PI-NN controller, as mentioned before, are obtained by using the particle swarm optimization technique. The used I.M has the following nameplate: 3-ph I.M, 380V, 2.2 kW, 2 poles, 50 Hz, L s = 13.6 mH, L r = 11.4 mH, R s =2.3 Ω, R r = 3.4 Ω, rotor inertia= 4.5*10 ^-3 kg/m ² .

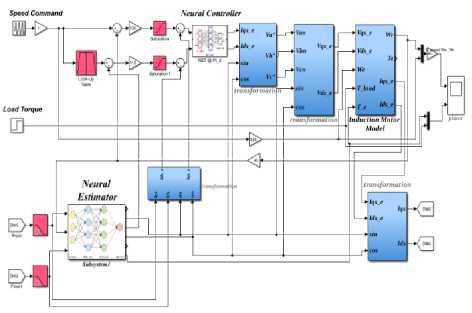
Fig.8. The overall system simulation

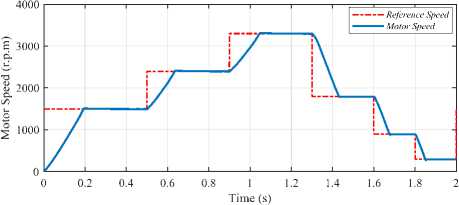
The performances of the DSP and ANN-systems, for different operating speeds under full-load condition, are depicted in Fig.9 and Fig.10 respectively.

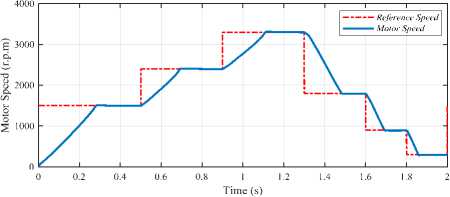
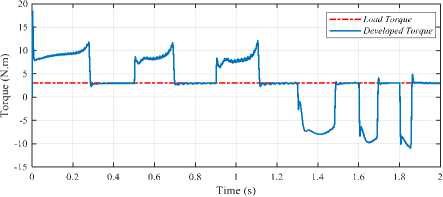
Fig.9. Speed and torque performance of DSP-based system

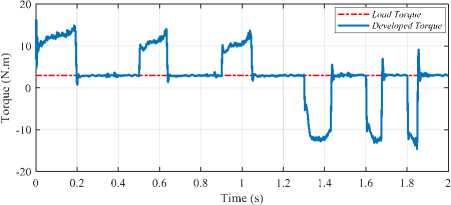
Fig.10. Speed and torque performance of ANN-based

Moreover, the performance of the motor in two quadrant operation, positive and negative load torque as well as zero speed, is investigated to examine the robustness degree of the ANN-based system, as shown in Fig.11.

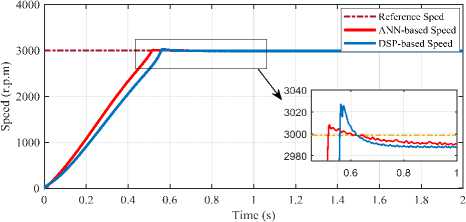
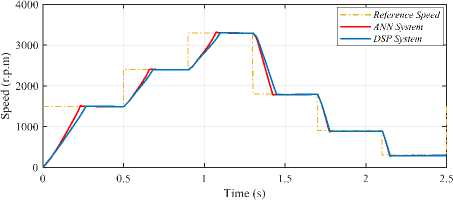
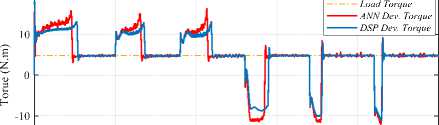
In addition, a comparison performance between the DSP and ANN-based systems are studied, to illustrate the feature of the proposed method, under full load and rated speed conditions as shown in Fig.12. Also, it investigated under variable speed and full load condition as shown in Fig.13.

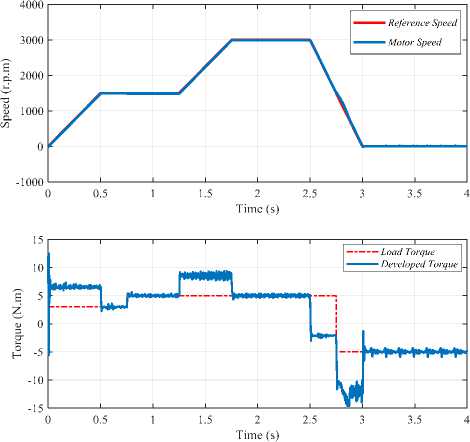
Fig.11. Two quadrant operation

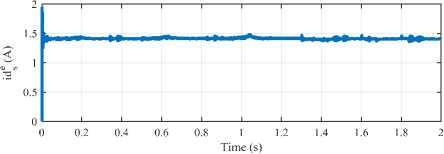
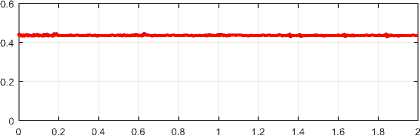
Furthermore, the effectiveness of the decoupling process can be inspected by the relationship between the q-axis current component and the developed torque, also the d-axis current component and the rotor flux as shown in Fig.14 and Fig.15 respectively.

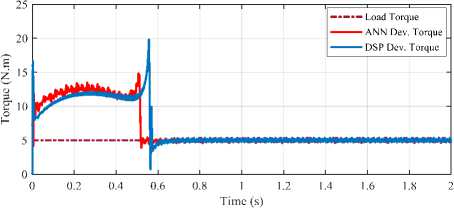
Fig.12. Comparison performance between DSP and ANN-based system, under hard step speed command and full-load condition

-20 --------------------------------1--------------------------------1--------------------------------1--------------------------------1--------------------------------

0               0.5                1                1.5               2               2.5

Time (s)

Fig.13. comparison performance between DSP and ANN-based system, under stair steps speed command and full-load condition

For further verification and to realize the robustness of the proposed controller, a comparison investigated is made between this controller and the presented system in [14] as different environments. The speed tracking performance shows slightly improving in the transient response as depicted in Fig.16. Also, Fig.17 shows the electromagnetic torque for both of the proposed and reference systems. These results demonstrate that the proposed controller has significant robustness which enabling it to experience the various changes associated with different operating conditions and for different types of motors, which achieves high operating stability and excellent performance for various loads.

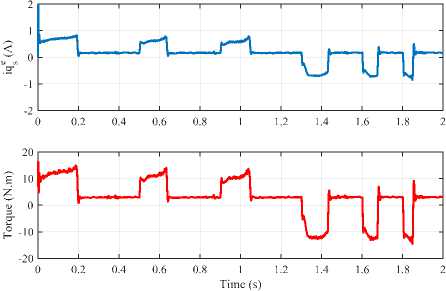
Fig.14. The relationship between ^$ and the torque

and ANN estimating and controlling strategies. The derivations may be summarized as following:

Obviously, FOC is a powerful complex controller in line with excessive overall performance demand, which gives a strong performance in various operation steps, underneath full-load circumstance in both variable torque and weakening field operation regions.

Implementing of Neural estimator and controller does not only reduce the complexity of the hardware, but it improves the overall system performance, which gives: overshot less than 0.5%, rise time 0.514 s, steady state error less than 0.2%, settling time 0.7 s. in conjunction with that of DSP-based performance: overshot about 2%, rise time 0.64 s, steady state error less than 0.4%, settling time 0.75 s.

Airgap Flux (weber)

Time (s)

Fig.15. The relationship between ^ds and the flux

The decoupling of the stator current components is exactly aligned on the dq-axis. The torque current ( lq_S ) is precisely analogous the electromagnetic torque (T e ) as proven in Fig.14, and the flux current ( ^ds ) is regular and precisely analogous the airgap flux as proven in Fig.15. The investigation results with other system presented in [14] prove that the proposed controller has considerable robustness which enabling the system to overcome various changes associated with different operating conditions and for different types of motors, which achieves high operating stability and excellent performance for various loads.