Асимптоматическое интегрирование дифференциальных уравнений типа Эмдена-Фаулера

Решение уравнений типа Эмдена-Фаулера изучалось во многих работах. Интерес к этой задаче не теряется и в настоящее время. Данное уравнение находит свое применение при решении многих прикладных задач. Например, в работе [1] оно лежит в основе математической модели конкурентоспособности и производительности некоторого предприятия. Конкурентоспособность F ( P ( n ) ) является степенной функцией от производительности P ( n ) , причем существуют такие константы p >  0 и k , при которых

F ( р ( n ) ) = р ( n ) p n k ,

Physics and Mathematics где n – номер исследуемой струк- туры предприятия.

Производительность P (n) > P0 и F пропорционально второй производной P по n . Для d2 P (n)

F (P (n )) = M (n) ^V ’ как правило, M (n) = n . В результате получим урав- нение с начальными условиями:

nP(n) -P(n)p nk = 0,n > n0, P(n0) = Po > 0,P'(n0 ) = P1.

Обзор литературы

Для уравнений типа Эмдена-Фау-лера получены существенные резуль- 441

таты, которые не только дополняют классические исследования, изложенные в монографии Р. Беллмана [2], но и демонстрируют практическое применение полученных результатов. Постоянный интерес обусловлен также тем, что уравнение широко применяется в различных областях, от экономики до математической физики.

Первоначально уравнение рассматривалось в виде:

(tsu')‘± tun = 0 , где δ,γ, n – постоянные.

Оно было получено Р. Эмдоном в связи с изучением условий равновесия политропного газового шара. Новые свойства решений уравнения Эмдена-Фаулера, касающиеся их продолжимости, были получены в исследованиях китайских математиков Чанга и Ли [1; 3–6]. Систематическое изложение результатов анализа продолжимости решения приведено в работах В. С. Самовола [7–8]. Вопрос существования решений для квазилинейных дифференциальных уравнений типа Эмдена-Фаулера высокого порядка исследуется в работе И. В. Асташовой [9].

Материалы и методы

Для исследования решений уравнения Эмдена-Фаулера применялся метод асимптотической эквивалентности. Нами было исследовано дифференциальное уравнение n-ого порядка, которое при n = 2 превращается в уравнение Эмдена-Фаулера.

Рассмотрим данное дифференциальное уравнение:

У⁽ n ⁾ = ^{ф (}t )1 У ^{| Л} sgn У ,          ⁽¹⁾

где t е [ T , +« ) , T >  1, X >  0, n >  1 - целое ф е C ([ T , +» )) .

Докажем асимптотическую эквивалентность по Брауеру уравнения (1) и уравнения

x ⁽ n ⁾ = 0 .                    (2)

Ясно, что выражения (1–2) представляются соответствующими системами, при этом можно было бы прибегнуть к результатам работы [4]. Однако новые методы доказательства асимптотической эквивалентности были применены именно для уравнения (1). При этом для простоты изложения в данной статье не рассматривается задача покомпонентной асимптотической эквивалентности.

Обратимся к условиям, при которых существуют решения уравнения (1), имеющие при t ^ +да вид:

y ( t ) — а о t + a i t    + ...

... + a n - 2 1 + a n - 1 + o (1).

Некоторые асимптотические свойства этого уравнения были рассмотрены в работе Р. Беллмана [2]; при n = 2, a 0 * 0 эта задача была решена Е. В. Воскресенским. В данном случае она решается при произвольном натуральном n и произвольном наборе чисел ( a ₀,..., a n - 1 ) на основе метода асимптотической эквивалентности [10–13].

Результаты исследования

Результаты проведенного исследования сформулируем в виде следующих теорем.

Теорема 1

Если 0 <  X <  1 и

+∞ +∞  +∞

' S S n - 1

при t ^ +^, то все решения уравнения (1) имеют вид (3).

Доказательство:

На множестве T < t0 < t < +^ запишем уравнение y (t) = a 0 tn-1 + a1 tn -2 +

+ ... ⁺ a n - 2 t ⁺ a n - 1 ⁺

⁽ n ^{- 1)!}

t j (t - s)n-1Ф (s) | y (s) |A sgn y (s)ds. (4) t 0

Тогда |^^ < c + c о J | ф( s )|| y (s )|л ds, t о где c, c0 > 0 , и на основании теоремы 1.1 из работы [13] запишем:

| у ⁽ t )| < c t n ^{- 1} , t >  t ₀ ,          (5)

где

У ⁽ t о ) = y 0 , y '( 1 ₀) = y ‘ ,..., y ⁽ n ^{- 1) (} t ₀) = y 0 n ^{- 1)} ; t ₀ – достаточно большое число, зависящее от чисел y ₀,..., y 0 n ^{- 1)} .

Поскольку

1 t

⁽ t ^- s ) n ^{- 1 ф (} s ) | y ( s ) ^{| Л} sgn y ( s ) ds =

⁽ n ^{- 1)!}

t 0

то из равенства (4), неравенства (5) и условия теоремы получим:

y ( t ) = b ₀ t n ^{- 1} + b_x t n — ² + ... + b n - 2 1 + b n ₄ + О (1) .

Приняв в качестве уравнения сравнения уравнение вида:

dZ = c ₀| ф ( t )| t ^{2 ( n - 1)} z ²            (6)

dt и, применяя теорему 1.1 из работы [Там же], убедимся в равномерной ограниченности решений этого уравнения при любом c0 ≥ 0 на множестве D = {z :0 < z < K, t > T > 1}, где K -произвольное фиксированное число, 0 < X < 1.

На основании теоремы сравнения и равномерной ограниченности решений уравнения (6) неравенство (5) справедливо при достаточно большом T и произвольных, но достаточно малых y ₀,..., y 0 ^{n - 1)} . Поэтому оценка (5) равномерна относительно t , и при достаточно большом T все решения уравнения (1) y ( t о ) = y o , y '( t o ) = y 0 ,..., У ⁽ n ^{- 1)} ( t o ) = У 0n ^{- 1)} имеют вид (3).

Доказательство закончено.

Теорема 2

Пусть выполняются условия теоремы 1, а

¹ S 1 S j - 1

существует и интегрируема на любом компакте из [ в , +да ) при всех j = 1, n . Тогда для любого набора действительных чисел ( a ₀, a 1 ,...,a n - 1 ) существует такое решение y ( t ) уравнения (1), при котором

y ( t ) = a_ht + a, t + ... + a tt + a + o (1) 0            1                    n — 2       n — 1

при t ^ +ЭТ .

Доказательство:

При t ₀ ≥ T рассмотрим семейство решений уравнения (1):

У (t) = aо t + ■■■ + an-21 + an-i + t +«  +«

+ ( - 1) ^{n - 1} jj ■■■ J Ф (S n )| y ( S n ) Г sgn y (S n ) ds i ... ds n , t S 1 S n - 1

при котором выполняются все условия теоремы 1.1 из работы [Там же]. Отсюда следует равномерная ограниченность семейства { v ( t )} . Поскольку при любых t, t >  1

t +∞   +∞

| V ( t ) - V ( t ) | < J J ... J | ф ( S n ) | s n ^{( n - 1)} c ^x ds_x ... ds n , ‘ S 1 S n - 1

то это семейство равностепенно непрерывно и, таким образом, компактно. Поэтому существует последовательность { t ₀ } , сводящаяся к функции y ( t ) равномерно на каждом компакте

| y(t) -a0tn-1 -...-an-1 | ≤ t +∞  +∞

t S 1 S n - 1

Из этого следует доказательство теоремы.

Доказательство закончено.

Следствие 1

При условиях теоремы 2 уравнение (1) имеет равномерно ограниченные решения с начальными данными У (t 0 ) = У 0 , y′(t0) = (-1)n+1 ×

У ⁽ n ^{- 1)} ( t о ) =

= - J ф( Sn-1) | У (Sn-1) Г sgn У (Sn-1) dsi... dsn-1 , tо удовлетворяющее данному условию y(t0) = y0. Справедливость следствия вытекает из теоремы 2 и теоремы 1 работы [5].

Следствие 2

Теорему 2 можно сформулировать в терминах асимптотической эквивалентности: уравнения (1–2) асимптотически эквивалентны по Брауеру, если выполняются условия теоремы 1 и

+∞ +∞  +∞

Y y W = J J ... J ф ( _Sy )|^^{( n - 1}Vv„ds j

¹ S 1 S y - 1

существует и интегрируема на любом компакте из [ в , +” ) при всех ^j = 1, n .

Применим полученные результаты непосредственно к уравнению Эмде-на-Фаулера:

u ′′ ± t ^σ uⁿ = 0 , (7)

a где n = - > 1, a - натуральное число, b – неbчетное натуральное число. Уравнение (7) можно записать в виде системы:

dz = Az ± L ( t , z ) , dt

где

( oo ) , ,   „ Л 1 )

A =          ; L ( t, z ) = t z ;

(1 0 J              2 (0 J z1 | (u '^

z ₂ J = I u J .

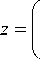
Пусть z = diag{1, t}eAy . Тогда уравнение (8) перейдет в уравнение y ‘ = t-1Лy ± g(t, y) ,            (9)

где      Л = diag {0, - 1}; g ( t , y ) =

= e - A diag {1, t ^{- 1} } • R ( t, diag (1, t ) e A y ), ( f n" )

R ( t , z ) = 1      ² I и

II g ( t , У )|| ^ c l t^c 2 I У 2 I n ^ ct ^a z ^{a +} n -|| y||n , c >  0.

Для определенности в уравнении (9) примем знак плюс, в противном случае рассуждения будут аналогичными. Пусть ст + n = - q .

Теорема 3

Если q > 2 , то уравнения (9) и dη =t-1Λη          (10)

dt в некоторой окрестности нулевого решения у = 0 асимптотически эквивалентны по Брауеру относительно функции I/ = t2-q при t ^+^, то есть

y ( t : t 0 , y o ) = n ( t : t 0 , ^z o ) ⁺ o ( t ^{2 -} q ), t ^ t 0 . (11)

Доказательство этой теоремы вытекает из теоремы 2, поскольку в этом случае все условия выполняются. Действительно, асимптотическую формулу (11) запишем в следующем виде:

y ( t : 1 0 , y o ) = 1 ₀

Тогда

У ( t ^: t о , У o ) = 1 ₀

o ]            2

_t - 1 I ^z 0 ⁺ o ⁽ t q ), t ^ t 0 .

о ]            2

t - 1 I z 0 + o ⁽ t ^q ), t >  t 0 ,

то есть

z (t) =

Г 1 о Y1 0 ^

l о t Л1 1J

1 0

0 t ^{- 1}

z0 + o (t2-q) ,

t > t 0 .

Тогда, если c ₁ = z ₂ ⁰ , c ₂ = z ₁ ⁰ , то

un = cn + o(t2-q) + tn (cn + o(12-q)), t > 10.

Поэтому при малых c 1 , c 2 получим:

u'(t) = c 2

+x

- J s ^a u n ( s ) ds =

t

t

a + n + 1

a + n + 1

( cn + o (t2-q)) +

ta + 1

+(c, + o (t q))+c, + tc-,, t > t ; 11                            1         2             0

,a + n + 2

u (t) =------------------------(cn + o (t2-q)) +

( a + n + 2)( a + n + 1) ²

, a + 2

+---------------(cn + o (t2-q)) +

(a + 2)(a +1) 1

+c1 + tc2, t > 10.            (12)

Доказательство закончено.

Обсуждение и заключения

На основании представленных в статье теорем и проведенного доказательства можно сделать вывод, что полученная асимптотическая формула (12) является более точной, чем соответствующие формулы Р. Беллмана.