Асимптотическая нормальность размера гигантской компоненты в случайном двудольном графе
Автор: Захаров П.А., Шабанов Д.А.
Журнал: Труды Московского физико-технического института @trudy-mipt
Рубрика: Математика
Статья в выпуске: 1 (57) т.15, 2023 года.
Бесплатный доступ
В работе исследуется предельное распределение размера так называемой гигантской компоненты в случайном двудольном графе G(n, n, p) в разреженном случае, когда p = c/n для некоторого фиксированного c > 1. Доказано, что распределение размера гигантской компоненты является асимптотически нормальным.
Случайные графы, компоненты связности, двудольные графы, асимптотическая нормальность
Короткий адрес: https://sciup.org/142238146
IDR: 142238146 | УДК: 519.179.4
Текст научной статьи Асимптотическая нормальность размера гигантской компоненты в случайном двудольном графе
1. Введение и история задачи
В работе исследуется предельное распределение максимального размера, компоненты связности в случайном двудольном графе G(n, n,p) Сначала напомним основные определения.
1.1. Основные определения
Одной из классических моделей случайных графов является знаменитая модель Эрдеша - Реньи G(n,p) В данной модели между каждой парой вершин из некоторого n-элементного множества ребра проводятся случайно и независимо от других с вероятностью р. По сути, мы имеем дело со схемой Бернулли на ребрах полного графа Кп нa n вершинах.
Модель G(n,p) — это центральный объект изучения теории случайных графов, но далеко не единственный. Очень активно изучаются обобщения этой модели, в которых схема. Бернулли проводится изначально на ребрах некоторого другого графа, не Кп. В настоящей работе мы рассматриваем модель случайного двудольного графа G(n,n,p), в которой основой выступает полный двудольный граф КП)Гг. Напомним, что в графе КП)Гг имеется два непересекающихся множества по n вершин — доли графа, между вершинами из разных
«Московский физико-технический институт (национальный исследовательский университет)», 2023
долей есть все возможные ребра, и нет никаких ребер между вершинами из одной и той же доли. Случайным графом G(n, п,р) называется случайный элемент, получающийся в результате схемы Бернулли на ребрах Кп,п: каждое ребро удаляется из графа независимо от остальных с вероятностью 1 — р.
1.2. Известные результаты
Одним из первых фундаментальных результатов относительно модели G(n,p) является открытие П. Эрдешем и А. Реньи [1] феномена двойного скачка максимального размера компоненты G(п,p) при переходе значения р порога 1/п. Обозначим через С^(п) г-й по величине размер компоненты случайного графа G(n, р), т.е., в частности, С1(п) — это максимальный размер компоненты G(п,p). В данных обозначениях результат Эрдеша и Реньи можно сформулировать следующим образом.
Теорема 1. (П. Эрдеш, А. Реньи, [1]). Пусть р = с/п, где с > 0, фиксировано и не зависит от п.
-
1) Если с < 1, то имеет место следующая сходимость но вероятности:
Сі(п) р 1
—--> а(с) =----------, п ^ то.
-
2) Если с = 1, то С1(п) имеет порядок п2/3 по вероятности:
Сі (п) = ӨР(п2/3).
Последнее означает, что для любой растущей функции ю(п) ^ +то выполнено Р(п2/3/w(n) ^ С1(п) ^ п2/3ш(п)) ^ 1 при п ^ то.
-
3) Если мсе с > 1, то имеет место следующая сходимость по вероятности:
С1(п) Р д, X
--> 3(с), п ^ то, п где 3(с) — это единственное решение уравнения 3 + е Зс = 1 на интервале (0,1). При этом
С2(п) 1
п ^ то.
' “(с) = с — ln с — 1 ,
Тем самым при переходе значения параметра р через 1/п порядок роста максимального размера компоненты G(n,p) меняется сначала от ln п до п2/3, а нотом — от п2/3 до п. Более того, в последнем случае компонента линейного размера единственна, а остальные по-прежнему имеют логарифмический размер. Тем самым, естественно называть подобную компоненту «гигантской».
Результаты теоремы 1 в дальнейшем уточнялись. В частности, В.Е. Степановым [2] была уставлена асимптотическая нормальность размера гигантской компоненты.
Теорема 2. (В.Е. Степанов, [2]). Пусть пр ^ с, где с> 1. Тогда имеет место следующая сходимость по распределению:
л/п
( С1(п) п
— 3 ) > -^ (0, С^),
п ^ то,
где 3 = 3(с) — это единственное решение уравнения 3 + е Зс = 1 на интервале (0,1), а 2 /З(1-Щ
° = (1-с(1-/З))2 '
Оригинальное доказательство Степанова весьма громоздко и опирается на точную асимптотику вероятности связности случайного графа. В 2012 году Боллобаш и Риордан предложили [3] короткое доказательство теоремы с помощью центральной предельной теоремы для мартингалов. Долгое время оставался открытым вопрос о пределвном распределении Сі(п) внутри фазового перехода (ситуация 2) в теореме 1). Он был решен Д. Олдосом [4] толвко в 1997 году.
Феномен фазового перехода в структуре компонент связности оказался общим для многих моделей. Результаты, аналогичные теореме 1, были установлены, например, для случайного гиперграфа (см. [5]), для случайного подграфа в гиперкубе (см. [7]), для случайного подграфа в квазислучайных графах (см. [6]). Однако в указанных работах при обсуждении размера гигантской компоненты речь шла только об асимптотике, о «законе больших чисел», если выражаться языком теории вероятностей. Нахождение точных предельных распределений оказалось гораздо более трудной задачей, но, например, в работах [8] и [9] был доказан аналог теоремы 2 для размера гигантской компоненты в случайном гиперграфе.
Изучение размеров компонент связности случайного двудольного графа G(n,n,p) также проводилось рядом исследователей. В [10] автор получил аналог теоремы 1 для G(n,n,p). Сформулируем его более точно, обозначив через L^d г-й по величине размер компоненты случайного графа G(n, п,р).
Теорема 3. (Т. Йоханссон, [10]). Пусть пр 3 с при п 3 то, г де с > 0 — фиксировано.
-
1) Если с < 1, то существует такая А = А(с), что
- Р (Ті(п) ^ А • lnп) —3 1, п 3 то.
-
2) Если эюе с > 1, то имеет место следующая сходимость по вероятности:
-3 23(e), п 3 то, п
где 3(с) ~ это единственное решение уравнения 3 + е-/3с = 1 на интервале (0,1). При этом существует такая В = В (с), что
Р (L2 (п) ^ В • ln п) —3 1, п 3 то.
В работе [11] исследовались размеры компонент связности G(п,п,p) при пр 3 1. Читатель также может найти в списке литературы в [11] ссылки на другие статьи по данной тематике.
1.3. Новый результат
Основной результат настоящей работы состоит в усилении теоремы 3 и обосновании асимптотической нормальности максимального размера компонент Lid случайного двудольного графа G(п, п,р) в ситуации, когда есть гигантская компонента.
Теорема 4. Пусть рп 3 с при п 3 то, г де с > 1 — фиксировано. Тогда имеет место следующая сходимость по распределению:
фп
б Lid у п
— 23^ -3 N (0, 2и2), п 3 то,
где 3 = 3(с) — это единственное: решение: уравнения 3 + е ^ = 1 ни интервале: (0,1). а
2 /3(1-Щ
^ (1-с(1-/3))2 •
Перейдем к доказательству теоремы 4.
2. Доказательство теоремы 4
Мы докажем следующую лемму, из которой будет следовать утверждение теоремы 4.
Лемма 1. Пусть G(1)(n,p), G(2)(n,p) — независимые случайные графы в модели Эрдеша-Ренъи, а С (1)(п), С (2)(п) — максимальные размеры их компонент соответственно. Существует такая случайная величина Си - что для всех п
Li(n) + ^п = С (1)(п) + С (2)(п), (2)
-
и, кроме того, ^п(Vn ^ 0 при п ^ +то.
Действительно, если лемма 1 выполнена, то по теореме 2 в силу независимости G(1')(n,p) и G(2)(n,p):
VS ( С ' 1) ( п )+ С (2) ( n ) - 2v) ЛМ (0,2,2).
С другой стороны, по лемме 1 туда же сходится последовательность
V- /wh. - 2л = ^ /ГЮ) - 2^s + & у п у у п у Дп
2.1. Процедура набора компонент связности
что в совокупности с условием Сп/у/п ^ 0 доказывает (1).
Далее мы опишем план доказательства леммы 2 с помощью процедуры набора компонент связности.
В работе [9] приведен следующий процесс набора компонент связности случайного графа G(n,p) с множеством вершин V..
-
1) На каждом шаге t = 0,1, 2,... у нас есть три множества St, At , Ut и чиело Сt, г де St — это множество рассмотренных вершин, At — множество активных вершин, Ut — множество неактивных вершин, Сt — число набранных компонент к моменту времени t. В начальный момент времени мы произвольным образом выбираем вершину v и полагаем A q = {v}, So = 0, U q = V. \ {v}, Со = 0.
-
2) Пусть (St, At, Ut, Сt) построены. Если | At | > 0, то на шаге t + 1 мы берем вершину vt — первую активную вершину из At и выявляем Xt+1 — множество ее соседей в Ut. Тогда полагаем:
St+1 = St U {vt}, At+1 =Xt+1 ^At \{vt}, Ut+1 = Ut \Xt+1, Сt+1 =Сt.
-
3) Если |At| = 0, но \Ut\ > 0, то текущая компонента набрана и надо переходить к следующей. На шаге t +1 мы берем вершину vt — первую неактивную вершину из Ut и полагаем:
St+1 = St, At+1 = {vt}, Ut+1 = Ut \{vt}, Сt+1 =Сt + 1.
-
4) Если |At| = 0 и \Ut\ = 0, то процедура завершается.
Отметим, что случайная величина |Xt+1|, число новых добавляемых активных вершин, имеет условное биномиальное распределение Bгn(|Ut|,p'), если имеется текущая активная вершина.
Для двудольного графа G(n, п, р) мы немного изменим процедуру, чтобы процесс набора шел параллельно в обеих долях. Пусть V.1) и V.2) — это доли графа G(n, п,р).
-
1) На каждом шаге t = 0,1, 2,... у нас есть две четверки (St(*), А^, u"^ , Ct) г = 1, 2, (*) (*)
где St — это множество рассмотренных вершин в г-н доле, А/ — множество активных вершин в г-й доле, Ц*) — множество неактивных вершин в г-й доле, Ct — число набранных компонент к моменту времени t. В начальный момент времени мы произвольным образом выбираем вершину г € v "1 и полагаем Ao1 = {г}, А02) = 0, S^* = 0, г = 1,2, Uo(1) = к(1) \ {г}, Uo(1) = V„(2), Co = 0.
-
2) Пусть (S(), А/*), и/’), Ct), г = 1, 2, построены. Если |А^)| > 0, г = 1, 2, то на шаге t + 1 мы берем вершины г^, г = 1, 2, — первые активные вершины из А^ соответственно, и выявляем Xt(+i — множество их соседей в Ut(3 г), г = 1, 2, т.е. мы берем соседей среди неактивных вершин противоположной доли. Тогда полагаем, как и ранее:
с (*) _ сД) I I /Д*)! Л (0 _ v (3—0 । । Д*) \ /Д*)! тД*) _ тД*) \ X (3—*) С _ С
St+1 = St U{rt }, At+1 Л/.1 UAt \{г/ }, Ut+1 = Ut \At+1 , Ct+1 = C/.
-
3) Если же, например, |А(1)| > 0, но |At2)| = 0, то компонента еще не закончена, поэтому на шаге t + 1 мы будем добавлять только соседей активной вершины из первой доли. Берем вершину г(1) — первую активную вершину из А/1), выявляем Х^ — множество ее соседей в Ut(2). Тогда полагаем:
с (1) _ с(1) и гу(1) (1) (1) \ тД2) — тД2) \ х(1) (2) — Х(1)
St+1 = St U {г/ }, At+1 = At \{rt }, Ut+1 = Ut \At+1, At+1 = A/-r
Все остальные элементы не меняются. Ситуация |А(1)| = 0, но |А/2)| > 0 полностью симметрична.
-
4) Если | А/*) | = 0, г = 1, 2, н о |U/(1) U Ut(2) | > 0, то компонента за кончена. На шаге t + 1 мы берем вершину г/*) — первую неактивную вершину из ЦД, которое не пусто, и полагаем:
А^ = {г"*)}, U^ U \{гС*)}, C/+1 =С/ + 1.
Остальные величины значений не меняют.
-
5) Если | A/1) U А/ 2) | = 0 и і Ц 1 U Ц 2)| = 0, то процедура завершается.
Теперь опишем план доказательства леммы 1. Пусть То — это момент времени, в который начинается набор гигантской компоненты G(n, п,р) Мы докажем, что он наступит достаточно быстро
Предложение 1. Выполнено
Р (То < (ln п)2) —> 1, п ^ то.
Далее, при наборе гигантской компоненты нас будет интересовать момент времени, в который оба множества активных вершин будут достаточно велики. Положим to = Р(1 + (с — 1)/8)п1/4Д Мы проверим, что в момент времени to как раз подходит. Имеет место следующее утверждение.
Предложение 2. Существует такая а = а(с) > 0, что выполнено
Р ^|А/1) | > ап1/4, |А/2) | ^ ап1/4^ —> 1, п ^ то.
Далее, обозначим тп = min{t : t > to, |А/1)| = 0 ил и |А/2)| = 0} — это первый момент времени после to, в который в одной из долей пропадают активные вершины. Заметим, что для любого t € (to,Tn) выполняются равенства
|А/*>| = | а /*2 1 | — 1 + |Х/(3-г)|, г = 1,2.
Далее, случайная величина Х( г) будет иметь условное биномиальное распределение с параметрами Вгп(|и()|,р), где
t lUl = п — £ хl — Q^l, j=t0
где Q^ = А^) U S^ — множество активных или рассмотренных вершин в момент времени tg в Тй доле. Ясно, что IS^l С tg = о(Дп). Простым применением неравенства Маркова можно убедиться, что и множества А^) будут не слишком велики.
Предложение 3. Для каждого г = 1, 2 выполнено
Р (|^t0) | С п1/3^ —> 1, п ^ то.
Таким образом, при t Е (tg, т^) наш процесс набора компоненты будет похож на параллельную работу процедуры для двух случайных графов G(n,p) в модели Эрдеша-Реньи. Более того, при фиксированных наборах (S^, At0, U^, Ct0 ), г = 1, 2, мы получим независимые процессы, т.е. фактически мы запустили процедуру на независимых случайных графах G(1)(n,p), G(2)(n,p) и параллельно набираем в них гигантские компоненты. Учитывая, что в момент времени tg у нас уже есть большое число активных вершин в каждой доле (больше, чем по теореме 1, есть в негигантских компонентах), мы можем сделать вывод, что с точностью до о(Дп) величина тп совпадает по распределению с min(C(1)(п),С(2)(п)). Поймем теперь, как связаны Т1(п) и тп. Ясно, что в гигантскую компоненту мы заберем все рассмотренные вершины между моментами времени тп и Tg, их будет от 2тп —2tg до 2тп, т.к. между моментами времени tg и тп мы в каждый момент времени добавляем по 2 вершины в компоненту. Но в одной из долей могло остаться некоторое количество активных вершин. Обозначим его через Zni кроме того, обозначим через стп число тех вершин, что будут донабраны процедурой в гигантскую компоненту после момента времени тп. Следующее предложение говорит о том, какое распределение будет иметь данная величина.
Предложение 4. Выполнено
СТи — Z^ 1-с(1-9)
—> 0 п ^ то.
у п
Осталось разобраться с совместным распределением случайных величин (Zn, тп). Обозначим через Yn число активных вершин, которые останутся в одном случайном графе G(z)(n,p) в тот момент, когда во втором будет закончен набор гигантской компоненты.
Предложение 5. Существуют такие случайные величины ^, ^", что для всех п
(тп + ^ ,Z„ + <) = ^min(C(1)(п), С (2)(п)), үп) ,
п. кроме того. (l^'n| + ф"|)Д/п ^ 0 при п ^ +то.
2.2. Доказательство леммы 1
Наконец, мы готовы вывести лемму 1.
Во-первых, заметим, что из предложения 3 следует, что с вероятностью, стремящейся к 1, выполнено неравенство
|L1 (п) - an - 2т„| ^ 2to = О(п1/4), т.к. разность не превосходит количества рассмотренных вершин к моменту времени to. По предложению 4 получаем
1 L1(,1) - Z t • 1 - е(1 - ,)
- 2т„| = op(V^).
Наконец, из предложения 5 мы получаем, что с точностью op(Дп) случайная величина L1(n) совпадает по распредлению с
Гп • -----1 ---- +2min(С(1)(п),С(2)(п)).
1 - с(1 - ,)
Осталось заметить, что из доказательства предложения 4 (см. ниже) следует, что
^тт-щ-, -|С(1) (п) - С(2)(п)|
= op (Дй).
Но
| С (1) (п) - С (2) (п) | + min(С(1) (п), С (2) (п)) = С1 (п) + С2 (п).
Лемма 1 доказана, и мы переходим к доказательству предложений 1-5.
2.3. Доказательства вспомогательных утверждений
Доказательство предложения 1. Из доказательства теоремы 3 известно, что каждая вершина попадает в гигантскую компоненту с вероятностью ,(1+ o(1)). Предположим, что к моменту времени ti = P(lnп)2^ мы ещё не начали набирать гигантскую компоненту. Тогда из теоремы 3 следует, что с вероятностью, стремящейся к 1, мы набирали только компоненты, не превосходящие по размеру В • ln п. Отсюда следует, что к моменту времени ti мы уже полностью на брали не меньше, чем В-1 • ln п компонент.
Заметим, что, начиная очередную компоненту, мы каждый раз имели не менее п(1+о(1)) неактивных вершин, значит, вероятность начать гигантскую компоненту каждый раз была равна ,(1 + o(1)), и эти события не зависят от происходящего до этого. Значит, вероятность того, что ни одна из первых В-1 • lnп компонент не будет гигантской, не превосходит
(,(1 + о(1)))В-ЧпТ -^ 0 п ^го.
□
Доказательство предложения 2.. Положим ti = P(lnп)2^, t2 = ^п1/4^. Согласно предложению 1 нам достаточно рассмотреть ситуацию, когда гигантская компонента начала набираться до момента времени t1. Но сначала грубо оценим число активных вершин в момент времени П. Ясно, что добавляемое число активных вершин стохастически домини-руется случайной величиной с распределением Вгп(п,р). Тогда
Е|л£)| ^ npt1 = O(t1 ).
Следовательно, Р (Д(1) U |Я(2)| > |_п1/5_|) ^ 0 пр и п ^ го.
Рассмотрим процесс набора гигантской компоненты не в параллельной процедуре, а на каждом шаге ограничимся лишь одной активной вершиной в одной из долей. Посмотрим вероятность того, что после t Е [t2, 2t2] подобных шагов мы получим малое число активных вершин в сумме. Оценим вероятность того, что это число меньше (с — 1)t/2. Заметим, что вероятность этого события не превосходит вероятности того {^2j=tl Wj ^ ^^t + t}, где Wj — независимые биномиальные случайные величины Bin(n — ti — ^n1/5J — t — f5-1 t!,p)-ведь число соседей текущей активной вершины стохастически доминирует над данным распределением и одну вершину мы всегда убираем из активных. Значит, имеем верхнюю оценку
( t -, \ / t \
Е Wj ^ tl =Р I E(Wj — EWj) ^ t(1 + о(1)) l ^
j=ti ) \j=ti /
(неравенство Чернова)
(1 — c)2t2(1 + о(1>) (1 — с)2
« exp { —~---- 8 ct }=“Р Ь °(1))} <
Тем самым с вероятностью, стремящейся к 1, в каждый момент времени
t
Е [t2, 2t2] у нас будет как минимум активных (с — 1)t/2 вершин в наборе по одному. Для параллельного набора это означает, что в момент времени t2 будет вьшолнено 1^1) ^ ^t2)l ^ (с —
1)t-/2.
Без ограничения общности можно считать, что |Д(1)| ^ (с — 1)t2/4. Тогда в силу тех же рассуждений, что были приведены выше, с вероятностью, стремящейся к 1, после дополнительных (с — 1Д2/8 шагов набора активных вершин в первой доле останется как минимум (с — 1)t2/8. а во второй получится нс менее (с — 1)4/16 активных верш іш. □
Доказательство предложения 3.
Сначала оценим математическое число Д^)|. Заметим, что добавляемое число активных вершин на каждом шаге стохастически доми-нируется случайной величиной с распределением
Bin(n,pY
Тогда
Е4t0)l < ipto = O(n1/4). Следовательно, из неравенства Маркова следует, что Р(|П(г)| > п1/3) ^ 0 при 1 ^ то.
Доказательство предложения 4.
Для начала поймем, как выглядит ситуация в момент времени
тп,
когда одна в одной из долей уже закончились активные вершины, а во второй еще нет. У нас еще осталось
Zn
вершин в ней, без ограничения общности будем считать, что активные вершины остались в первой доле. Из предложения 5 следует, что
Zn
= Ор(Д1)- Тем самым в каждой доле у нас осталось (1—Д)1(1+о(1)) вершин. Учитывая, что с(1 — 3) < 1, мы фактически получаем ситуацию, когда из каждой оставшейся вершины первой доли будет запущен набор компоненты связности в рамках ситуации 1) теоремы 3. Согласно ей каждая компонента будет иметь всего лишь логарифмический размер, что оставляет на каждом шаге для каждой активной вершины (1 — 3)1(1 + о(1)) неактивных вершин для проверки на соседство. Тем самым,
оп
— это сумма размеров независимых компонент в случайном графе G((1 — 3)1(1 + o(1)),p).
Представим z.
On
= E^j (1), j=1
где
^j
(1) — это размер той компоненты в оставшемся графе, которую удалось набрать из j-й начальной активной вершины. Стало быть, равномерно по веем
j
^ п2/3
lim Еф (1) = n >х
Отсюда, пользуясь независимостью
^,(п)
и
Zn,
а также неравенством Чебышева, получаем
z„ an - ЕД(п) j=i Е^п =oQ равномерно по всем ж С п2/3. Отсюда получаем, что
--
- ЕЙт Efj(п) р п ------—=--> 0 п ^ то.
V п
Осталось заметить, что раз
Zn
= Ор (Дп), то
Z • 1-дЬ) — E^i ЕД (п) р -------— _--> 0 п ^ то.
V
п
□ Доказательство предложения 5. Здесь мы уже повторяем ранее приведенные аргументы. Начиная с момента времени ti, параллельный процесс набора компонент будет в точности повторять одновременный набор гигантских компонент в независимых случайных графах О(г)(п,р), г = 1, 2. Отличие состоит в О(п1/3) начальных вершинах, но теорема 2 верна всегда при пр ^ с. Тем самым эти вершины не могут повлиять на предельное распределение, в котором нам важна точность только порядка О(Дп). Стало быть, для некоторых случайных величин р'п, р", имеющих порядок ор(Дп), выполнено то + р", Z" + р") = ^min(C(1)(п), С(2)(п)), Уп) . Доказательство предложения 5 завершает доказательство теоремы 4.
3. Источники финансирования Исследование выполнено за счет гранта Российского научного фонда № 22-21-00411.
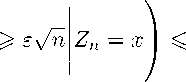
Список литературы Асимптотическая нормальность размера гигантской компоненты в случайном двудольном графе
- Erd˝os P., R´enyi A. On the evolution of random graphs // Publication of the Mathematical Institute of the Hungarian Academy of Sciences. 1960. V. 5. P. 17–61.
- Степанов В.Е. О вероятности связности случайного графа 𝒢𝑚(𝑡) // Теория вероятн. и ее примен. 1970. Т. 15, № 1. С. 55–67.
- Bollob´as B., Riordan O. Asymptotic normality of the size of the giant component via a random walk // Journal of Combinatorial Theory, Series B. 2012. V. 102. P. 53–61.
- Aldous D. Brownian excursions, critical random graphs and the multiplicative coalescent // The Annals of Probability. 1997. V. 25. P. 812–854.
- Schmidt-Pruzan J., Shamir E. Component structures in the evolution of random hypergraphs // Combinatorica. 1985. V. 5. P. 81–94.
- Frieze A., Krivelevich M., Martin R. The emergence of a giant component in random subgraphs of pseudo-random graphs // Random Structures and Algorithms. 2004. V. 24. P. 42–50.
- Ajtai M., Koml´os J., Szemer´edi E. Largest random component of a k-cube // Combinatorica. 1982. V. 2. P. 1–7.
- Behrisch M., Coja-Oghlan A., Kang M. The order of the giant component of random hypergraphs // Random Structures and Algorithms. 2010. V. 36. P. 149–184.
- Bollob´as B., Riordan O. Asymptotic Normality of the Size of the Giant Component in a Random Hypergraph // Random Structures and Algorithms. 2012. V. 41. P. 441–450.
- Johansson T. The giant component of the randombipartite graph // Master thesis in Engineering and Computational Science. 2012.
- Do T.A., Erde J., Kang M. Component behaviour and excess of random bipartite graphs near the critical point // arXiv.2105.14883. 2021.


