Асимптотическая устойчивость решений одного класса нелинейных дифференциальных уравнений второго порядка с параметрами

Настоящая работа продолжает исследования авторов [1–4] асимптотической устойчивости решений обыкновенных дифференциальных уравнений с периодическими коэффициентами. В работе [1] рассматривались линейные системы дифференциальных уравнений dx

"dt = A(t)x,     t > 0, где A(t) — матрица размера n х n с непрерывными T-периодическими элементами. В терминах разрешимости специальной краевой задачи для дифференциального матричного уравнения Ляпунова dtH + HA(t) + A*(t)H = -C (t)                         -

был установлен критерий асимптотической устойчивости нулевого решения системы (1).

Теорема 1. Нулевое решение системы (1) асимптотически устойчиво тогда и только тогда, когда существует эрмитово решение краевой задачи dtH + HA(t) + A*(t)H = -C(t),  0 < t < T,

H(0) = H(T) > 0, где C(t) — эрмитова положительно определенная матрица с непрерывными элементами на [0, T].

Отметим, что дифференциальные матричные уравнения вида (2) рассматривались во многих работах при исследовании качественного поведения решений дифференциальных уравнений с переменными коэффициентами (см., например, [5–10]).

Замечание 1. Если A(t) = A и C (t) = C постоянные матрицы, то краевая задача (3) эквивалентна матричному уравнению Ляпунова

HA + A * H = - C,    C = C * > 0,

• т. е. теорема 1 совпадает с критерием Ляпунова.

Используя решение H (t) краевой задачи (3), можно указать радиус круга, содержащего мультипликаторы системы (1), и получить оценки, характеризующие скорость убывания решений системы (1) на бесконечности [1].

Теорема 2. Если нулевое решение системы (1) асимптотически устойчиво, то для ее решений имеет место следующая оценка

t

• -1 \ Hhxs) \\ d^s

  , t > 0,

  
  
  
  

где H (t) — T-периодическое продолжение решения краевой задачи (3) на полуось { t >  0 } , h i (t) > 0 — минимальное собственное значение матрицы H(t), c i (t) > 0 — минимальное собственное значение матрицы C ( t ) .

Всюду мы используем спектральную матричную норму.

Замечание 2. Если A(t) = A постоянная матрица и C (t) = I , то оценка (4) совпадает с оценкой Крейна (см., например, [6]).

Замечание 3. Теоремы 1 и 2 позволяют проводить исследования асимптотической устойчивости нулевого решения системы (1), не переходя к решению задачи на собственные значения матрицы монодромии, т. е. без нахождения мультипликаторов.

С использованием перечисленных результатов в работах [2, 3] исследовалась асимптотическая устойчивость нулевого решения нелинейных систем dx

dt = A(t)x + f (t,x),     t> 0, где A(t) — матрица размера n x n с непрерывными T-периодическими элементами, f (t, x) — вещественнозначная гладкая вектор-функция, f (t, 0) = 0. В терминах решения H(t) краевой задачи (3) были получены оценки области притяжения нулевого решения и установлены оценки экспоненциального убывания решений системы (5) при t ^ го. Приведем формулировку результата из работы [3].

Теорема 3. Пусть нулевое решение системы (1) асимптотически устойчиво, и вектор-функция f (t, x) удовлетворяет условию

Re ( H(t)f (t, x),x }< q ( H(t)x,x } ^{1+ Y} ,   t >  0, x G C n , q >  0, y> 0.           (6)

Тогда нулевое решение системы (5) асимптотически устойчиво, и область

E = {x G Cn : (H(0)x,x)Y < r}, где

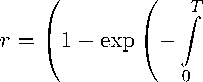
^Yc ^{1 (s)} _d8 I h (s) H

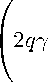
T

У exp

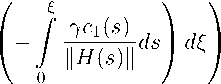
является областью притяжения нулевого решения. Для решения системы (5) с началь ными данными x(0) G E имеет место оценка

t

_ / ^c1 ^(s)

J IIH(s) H

ds / -( H⁽⁰_M⁰M⁰⁾_Ey     t> 0

r

В настоящей работе рассматриваются уравнения второго порядка следующего вида y" + apy + (в^2 + цу(€)Жу) = 0,    t > 0,

где a >  0, в <  0, Ц >  0 — параметры, ^(t) — непрерывная T -периодическая функция такая, что

T

У ^(s) ds = 0,                                       (8)

^(y ) — вещественнозначная гладкая вектор-функция, ^(0) = 0.

Цель работы — получить условия асимптотической устойчивости нулевого решения уравнения (7), установить оценки области притяжения нулевого решения и указать оценки скорости убывания решений уравнения (7) при t ^ го .

1.    Основные результаты

Вначале рассмотрим линейное уравнение y" + орр + (вц2 + w(t))y = 0,    t> 0,

где ц >  0, функция ^(t) удовлетворяет условию (8). Очевидно, что в случае в < 0 и ^(t) = 0 нулевое решение уравнения (9) является неустойчивым. Ниже мы докажем, что при наличии периодической функции ^(t) и определенных условиях на параметры а, в , Ц нулевое решение уравнения (9) будет асимптотически устойчиво.

При проведении рассуждений мы будем существенно опираться на результаты из работ [1–3]. В частности, мы будем использовать утверждения об асимптотической устойчивости нулевого решения систем дифференциальных уравнений следующего вида dx

— = д(Ах + A2(t))x + vg(t, x),     t> 0, где A1 — постоянная матрица размера nxn, спектр которой принадлежит левой полуплоскости {A G C : Re Л < 0}, A2(t) — матрица размера n x n с непрерывными T-периодическими T элементами такая, что У A2(t) dt = 0, ц, v — параметры, g(t, x) — вещественнозначная 0

гладкая вектор-функция такая, что g(t + T, x) = g (t, x) и

| g(t,x) | <  q | x | 1^{+ Y} , Y >  0, q = const.

Как известно (см., например, различные доказательства этого факта в [1, 6, 10]), при достаточно малых µ нулевое решение системы dx = ц(А1 + A2(t)>X'    t> 0,

dt асимптотически устойчиво. Отметим, что в [1] этот результат был доказан с использованием критерия, сформулированного в теореме 1. В [2] было показано, что если нулевое решение системы (11) асимптотически устойчиво, то при малых параметрах µ и ν нулевое решение системы (10) будет также асимптотически устойчиво, при этом были указаны диапазоны изменения параметров. Приведем соответствующее утверждение в случае y = 0. Для этого введем некоторые обозначения. Поскольку спектр матрицы A1 принадлежит левой полуплоскости, то существует единственное решение Hi = H* > 0 матричного уравнения Ляпунова

H 1 A 1 + A 1 H 1 = -I.

Обозначим через h _mi_n минимальное собственное значение матрицы H 1 .

Теорема 4. Пусть в1 =

tt max ||Hi A A2(t) dT + /"a2(t) dT Hi^, t∈[0,T]

Ц 1 =

h min

β 1 ^,

в2 = max t∈[0,T]

tt

|| [h i j A 2 (t ) dT + j A2(t ) dTH i] [A i + A 2 (t)] | ,

'2 = Ж ‘

Если параметры µ, ν удовлетворяют неравенствам

0 <ц< min { ^ i ,№ } , 2цв 2 + 2 | v | q (^ + в 1) <

1,

то нулевое решение системы (10) асимптотически устойчиво.

Перейдем к исследованию решений уравнения (9).

Теорема 5. Если а >  0 и

Tτ

T

T j I j V ^(s) ds I d^T >  I t ¹ j ^t^^{(t )dT}

β,

тогда при достаточно малых ц >  0 нулевое решение уравнения (9) асимптотически устойчиво.

Доказательство. При доказательстве мы будем следовать схеме рассуждений из работы [3]. Введем вектор-функцию vt)=( :;t;)-( y^y

В силу уравнения (9) имеем систему линейных дифференциальных уравнений dv

л = A^(t)v'

где

A(t) = ( „ 2 0           1 ) ■

• V ^{— в}м ^{2 —} M^^{(t) — a}M /

Сделаем следующую замену vi(t) = (1 + ^a(t))ui (t),      V2(t) = ^b(t)ui(t) + ^c(t)u2(t).

Покажем, что существуют T-периодические функции a(t), b(t), c(t) такие, что вектор-функция u(t) = uu12((tt))   удовлетворяет системе du

d" = MU (t,M)u

Вначале заметим, что в силу замены (15)

система (14) сводится к следующей системе

du dt

= U(t,^)u,

где элементы матрицы U(t, m) имеют вид

-            ^^(b(t) - a ‘ ^(t))    -               Mc^(t)

'      1 + _Kt) ’ u ^{12 (i}’^ri = r+H5 ’

^                                               b(t)(b(t) — a‘(t))\ u21(t, ^) = — c(t) ( в + ab(t) + ^ea(t) + y(t)a(t) +1 + ^a(t)     )

-

^b ‘ ^{(t) +} V ^{( t )} c(t)       ’

b(t) u 22 (i,^⁾- ^— M^ ⁺ г+ДО(о) ^—

cw

c(t)■

По аналогии с [3, § 3] возьмем c(t) = 1 и выберем функции a(t), b(t) так, чтобы

a ‘ (t) — b(t) = 0,      b ‘ (t) + ^(t) = 0.

Тогда действительно получаем систему (16), где

U (t,^) =

— в — ab(t) — ^ea(t) — ^(t)a(t) — a

1        \

1 + ^a(t) b(t)

.

-

1 + ^a(t) /

Используя представление

1      = 1       ( )     M 2 a 2 (t)

1 + ^a(t)        ^       1 + ^a(t), перепишем матрицу U(t,^) в виде

U (t,^) = U1 + U2(t,^) + ^2U3(t,^), где

- α ^,

= I T ^T

I — в — Tt / ^(т)а(т)dT

T

— ab(t) — ^a(t) - ^(t)a(t) + t f ^(t )а(т )dT

— ^a(t)

(^a(t) — 1)b(t)

U 3 ^(t,^⁾ =

\

^2^{( t )}     \

1 + ^a(t) a ² (t) b(t)

1 + ^a(t) /

Покажем, что существуют функции a(t) и b(t), удовлетворяющие условиям (17), такие, что спектр матрицы U i принадлежит левой полуплоскости, матрица U 2 (t, ^) является T -периодической и

T

У U 2 (t, ^) dT = 0.

В этом случае система (16) будет принадлежать классу систем вида (10), нулевое решение которых, как отмечалось выше, асимптотически устойчиво при малых µ.

Условия (17) подсказывают, что функции a(t), b(t) можно искать в виде

t

b(t) = — t1

^(s) ds,

ts

'— t2 t1

у(£)d£ ds,

при этом числа t i , t 2 G [0, T] следует выбирать так, чтобы выполнялись равенства

TT

У а(т) dT = 0,     У Ь(т) dT = 0.

Вначале построим функцию b(t). Заметим, что по теореме о среднем существует t i G [0, T] такое, что имеет место равенство

T

У т^(т)

T dT = T У ^(т)

t 1

dτ.

Учитывая, что

T

У т^(т) dT 0

TT

У У ^(s) ds dT,

T

T у y^(s) t 1

ds

TT

У У ^(s) ds dT, 0 t 1

(20) можно переписать в виде

Tτ

У У ^(s) dsdT = 0.

0 t 1

Возьмем функцию b(t) в виде (18) с указанным числом t i . В силу условия (8) функция b(t) является T -периодической, при этом из (21) имеем

T j Ь(т) dT = 0.

Построим теперь функцию a(t). Вначале покажем, что существует t 2 £ [0, T] такое, что выполнено соотношение

T

2 У ^T 2.^ ) 0

Ts dT + T j j .(t) t2 t1

dT ds =

T

T ²

-у j .^(t ) d^T.

t 1

Действительно, представим правую часть в виде

T

T ²

у j )

dτ

TT

s

.(t ) dT ds +

Ts

s

.(t ) dT ds.

0 s

0 t 1

Для первого слагаемого, очевидно, справедливо равенство

TT

s

.(t ) dT ds

0 s

T

2 j^т 2 ^ ^{( т} ) d^T. 0

Второе слагаемое по теореме о среднем можно записать в виде

Ts

Ts

s

0 t 1

.(t ) dTds = T j j .(t ) t 2 t 1

dτ ds,

где t 2 £ [0, T]. Отсюда получаем (22). Нетрудно показать, что (22) можно переписать в виде

Tτs

У У У .(6) di ds dT = 0.

0 t 2 t 1

Действительно, интегрируя по частям, имеем

Tτs /У/ .(i) di

0 t 2 t 1

ds dT = T

Ts

= ^T П . ^(t ) t 2 t 1

dτ ds

Ts

II ■ ■ ⁾

t 2 t 1

-

Ts

dτ ds

-

s

0 t 1

T t 2 Г , x з 1

у J .(T)^{dT +}2

t 1

.(t ) dT ds

T

У t ² .(t ) dT.

Отсюда вытекает, что соотношение (22) эквивалентно (23). Следовательно, функцию a(t) можно взять в виде (19) с указанным числом t 2 .

Покажем, что функция a(t) является T-периодической. Действительно, по определению имеем dt [a(t + T) — a(t)] = b(t + T) — b(t) = 0.

С другой стороны, учитывая свойства функции b(t), получаем

T

a(T)

-

a(0) = J" 0

b(s) ds = 0.

Отсюда a(t + T ) = a(t).

Итак, мы указали функции a(t) и b(t), удовлетворяющие условиям (17), такие, что матрица U 2 (t, ц) является T -периодической и

T

У U 2 (t, ц) dT = 0.

По определению спектр матрицы U1 принадлежит левой полуплоскости тогда и только тогда, когда а > 0 и

T e + TT j v(t)a(T)dT > 0

Покажем, что последнее неравенство эквивалентно условию (13). Для этого сделаем ряд преобразований. Применяя дважды формулу интегрирования по частям и учитывая условие (8), получаем

T

У <(т)а(т ) dT 0

τ

= j <⁽⁶⁾ d⁶

a(T)

T

Tτ

У У <⁽⁶⁾ d^{6 a (} T ^{) dT} =

В силу (19) имеем

τs у у ^(o de ds a(t)

Ts

= — / 1 ^ d6

ds a′

T

Tτs

+///'6 d6

ds a" (t ) dT =

Tτs

^{(T )+}Ш

^(6) d6 ds a'’ (t ) dT.

T j ^(т)а(т) dT =

Ts      T      Tτs

У У <0 ^⁶ds j _V⁽T)dT - j j j

^(6) d6 ds <(t ) dT.

Используя (20), получаем

T

У <(т)а(т ) dT = 0

Ts      T       Tτs

T j j <^{(6) d6}ds j t<⁽t ) dT -У У У 00      0       000

<(6) d6 ds <(t ) dT =

T

T

=T y—s)<(s) ds у

т<(т ) dT —

τs

У У <(6 ) ^6 ds

τ

TTτ

/ <(n)dn + 0

j I j<(6) d6 00

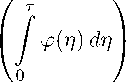
dτ.

Отсюда, учитывая условие (8), имеем

T j ^(т)а(т) dT =

T

T j W(t)

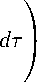
² T / т \ ²

+ УI у ^ de I dT.

В силу этого равенства получаем эквивалентность (24) и условия (13).

Следовательно, если выполнены условия теоремы, то спектр матрицы U 1 принадлежит левой полуплоскости. Тогда, как отмечалось выше, при малых µ нулевое решение системы (16) асимптотически устойчиво. Следовательно, асимптотически устойчиво нулевое решение системы (14), что влечет асимптотическую устойчивость нулевого решения уравнения (9).

Теорема доказана.

Замечание 4. Диапазон изменения параметра µ, при котором можно гарантировать асимп- тотическую устойчивость нулевого решения уравнения (9), может быть получен из теоре- мы 4. Действительно, возьмем в качестве Ai, A2(t) матрицы Ui, U2(t,ц) и v = ц3. Пусть

- 1

µ 3 <

I — min a(t) I t ∈ [0 ,T ]

— положительное число такое, что

2ц 3 в 2 + 2ц 2 max

^{3 2        3} t ∈ [0 ,T ]

Н^ЦЗ) ¹! ^IHi b ⁺ Ato)

< 1.

Тогда при

0 <  ц < min { ^ i ,^ 2 ,^ 3 }

нулевое решение уравнения (9) асимптотически устойчиво.

Пример 1. Пусть

lm

^(t) = У^ a k cos(kt) + УУ b j sin(jt).

k =1               j =1

Тогда условие (13) имеет вид

β>

- 2 b ( k ) 2 - 2 E j2 2 . k =1              j =1

Ниже мы покажем, что используя теоремы 1 и 2, можно получить оценки решений уравнения (9), характеризующие скорость убывания при t ^ го . Если выполнены условия теоремы 5, то нулевое решение системы (14) асимптотически устойчиво. Тогда, в силу теоремы 1, краевая задача (3) имеет единственное решение H (t) = H * (t), при этом, как показано в [1], H (t) > 0, t Е [0, T]. Поэтому, согласно теореме 2, для получения оценок экспоненциального убывания решений системы (14) достаточно построить решение краевой задачи (3) при некоторой матрице C (t) = C * (t) > 0. Вначале рассмотрим матрицу

H(t,^) = 1 Hi — H2(t,^), где Hi — решение уравнения Ляпунова (12) с Ai = Ui,

H 2 (t,^) = H i

t

У Ц 2 (т,ц) dT +

t

У и2;(т,ц) dTH i .

Нетрудно проверить, что она является решением краевой задачи вида (3) для системы (16)

d-H + цНи(t, ц) + ци * (t, ц) Н = -C (t, ц), 0 <  t <  T, dt

Н(0,ц) = Н(Т,ц) > 0, где

C (t,^) = I + цH 2 (t■ц)U(t,^) + ци *(t, ц)H 2 (t■ ц) - ц ² H 1 U з (t■ц) - ^ 2 U 3 * (t,^)H i .

Заметим, что C(t,ц) = C*(t, ц), причем в силу условия (25) на параметр ц эта матрица является положительно определенной. Введем матрицу

H (t,ц) = L * (t,ц) H (t,ц)L(t,ц),                             (26)

где

µ

L(t, ц) =

1 + цa(t) - b(t)

\   1 + цa(t)

Используя замену (15), нетрудно показать, что для системы (14) матрица H (t,ц) является решением краевой задачи (3)

dH + HA(t) + A*(t)H = -C(t,ц), 0 < t < T, H(0, ц) = H(Т,ц) > 0, где

^C (t,^) = ^L * ^(t,ц^{) c (t,}Ц^)L(t,Ц⁾•

Тогда, в силу теоремы 2, для решений системы (14) справедлива оценка (4). Отсюда получаем следующее утверждение.

Теорема 6. Пусть выполнены условия теоремы 5 и параметр µ удовлетворяет условию (25). Тогда для решений y(t) уравнения (9) имеет место следующая оценка

t

"/ ^С^Мг ds ■ t> 0, llH(8,ц)\\ где h1(t■ц) > 0 — минимальное собственное значение матрицы H(t■ц), определенной в (26), C1(t■ц) > 0 — минимальное собственное значение матрицы C(t■ц), определенной в (27).

Перейдем к рассмотрению нелинейного уравнения (7). Будем предполагать, что функция ^(y) удовлетворяет оценке

| ^(y) - ^ ‘ (0)y | <  p | y | ^{1+ s} ,      p> 0, 5> 0,                       (28)

причем ^‘(0) = 0. Перепишем уравнение (7) следующим образом у’’ + a^y' + (вц2 + цy(t))^‘(0)y + (вц2 + цy(t))(^(y) - ^‘(0)y) = 0.         (29)

Рассмотрим линейное уравнение у’’ + ацу’ + (вц2 + цy(t))V(0)y = 0,     t > 0.

Вводя обозначения в = вФ‘(0), ^(t) = ^(t)^‘(0), получаем уравнение вида (9), для решений которого справедливы доказанные выше утверждения.

Пусть y(t) — решение уравнения (7) систему иv(t) = (v2(t)) = (Уй )■ В силу(29) имеем

где

/ о

A(t) =     я 2

V - ^вц - W^t)

—ац

dv dt

,

A(t)v + f(t,v),

f ^(t,v)  ( ( вц ² + wWW — ^ ‘ (o)v i ) ) ■

Из (28) получаем

||f(t,v) |< PlM| ^{1+ 5} ,      P = ( 1 в | ц ² — Ц min p(t))p.

t e [0,T ]

Обозначим через H(t) решение краевой задачи (3) для дифференциального уравнения Ляпунова, построенное по указанной выше схеме для линейной системы dv dt

= A(t)v.

Учитывая условия на H (t) и f (t, v), получаем

,^^-

Re < H(t)f(t.v).v ) <  »H (t)Hf(i,v)Hv | < Ts P l H l+L ( H(t)v.v ) ^{1+ i/ 2} , t > 0, ^(h 1 ^(t))

где hi (t) — минимальное собственное значение матрицы H (t). Следовательно, система (30) входит в класс систем (5), правая часть которых удовлетворяет условию (6) с q >  PlH (t)l                                                                 „

~  ^1+^/2, Y = "/2- Тогда из теоремы 3 мы получаем область притяжения для нулево го решения уравнения (7) и оценки экспоненциального убывания решений уравнения (7) с начальными данными из этой области притяжения.

Замечание 5. В частном случае уравнение (7) совпадает с уравнением ≪ перевернутого маятника » (^(t) = sin t, ф(у) = sin у) с колеблющейся точкой подвеса по закону x(t) = a sin(t) [11, 12]. Указанные условия асимптотической устойчивости вида (13) совпадают с известными условиями Н.Н. Боголюбова, полученными методом усреднения (см., например, [13, 14]). К уравнению (7) сводится изучение колебаний ≪ перевернутого маятника ≫ , точка подвеса которого совершает произвольные периодические колебания.

Работа выполнена при поддержке ФЦП ≪ Научные и научно-педагогические кадры инновационной России ≫ на 2009–2013 гг. (государственный контракт № 16.740.11.0127, соглашение №14.B37.21.0355), Российского фонда фундаментальных исследований (проект № 10-01-00035) и Сибирского отделения Российской академии наук (междисциплинарный проект № 80).