Асимптотические решения скалярного волнового уравнения

В общем случае решение задач дифракции представляет собой сложную математическую задачу и требует специальных численных методов и больших вычислительных затрат [1, 2]. Асимптотические методы относятся к категории аналитических методов и играют большую роль. В ряде случаев они позволяют быстро и эффективно оценить результат, не прибегая к громоздким численным расчетам. Для развития новых асимптотических подходов для решения уравнений Максвелла (или уравнений акустических волн) целесообразно первоначально рассмотреть более простую задачу решения скалярного волнового уравнения. Асимптотическим методам решения уравнения Гельмгольца и посвящена настоящая работа.

Приближение геометрической оптики основано на асимптотическом методе решения уравнения Гельмгольца. Известные аналитические методы решения задач дифракции на дифракционных оптических элементах (ДОЭ) используют приближение геометрической оптики для расчета поля непосредственно за дифракционным микрорельефом [1, 2]. Целью данной работы является анализ геометрооптического подхода и построение новых асимптотических решений уравнения Гельмгольца, основанных на более точной локальной аппроксимации поля в рельефе полем в дифракционной решетке.

• 1.    Геометрооптический подход

В дифракционной оптике широко используются два асимптотических метода:

• 1.    лучевой метод или приближение геометрической оптики [3-5];

• 2.    метод перевала или метод стационарной фазы [3, 6].

Рассмотрим подробнее первый метод. Распространение света в скалярной теории описывается волновым уравнением Гельмгольца. В неоднородной среде уравнение имеет вид:

А Е ( x , y , z ) + k ² s ( x , y , z ) Е ( x , y , z ) = 0, (1) где k = 2n/X, X - длина волны, E - компонента комплексной амплитуды электрического поля, s - диэлектрическая проницаемость материала, (x, y, z) -декартовы координаты.

Представим комплексную амплитуду в показательной форме Е = A exp ( ik у ) , где A - амплитуда поля, у - эйконал поля и подставим ее в уравнение (1). В результате получим

ik ( 2 V A Vy + A Ay ) +

+ ( a a - k ² A ( Vy ) ² + k ² s A ) = 0.

Это комплексное уравнение соответствует системе двух уравнений

div ( A ²Vy ) = 0, ( Vy ) ² = s + kA.

В случае, когда свойства среды, амплитуда и фаза решения уравнения Гельмгольца изменяются медленно, система уравнений принимает следующий вид [3-5]:

div ( A ² Vy ) = 0, ( Vy ) ² =s .                   (4)

В этом случае уравнения перестают быть связанными друг с другом и их можно решать последовательно. Уравнения (4) называются уравнениями переноса и эйконала и описывают геометрооптический подход [3-5]. Геометрооптический метод является асимптотическим решением уравнения Гельмгольца при k ^ « .

Для того, чтобы найти решение системы уравнений (4), необходимо задать значения амплитуды и эйконала поля на некоторой начальной поверхности. Если начальная поверхность является плоскостью z = 0 и s = 1, то решение уравнений (4) можно записать в виде [5]

Е ( x , y , z ) =

=z

n

A ( u n , v n ^,0 ) ^ex p ( ik ( y ( u n , v n ^,0 ) + L n ( u n , v n ) ) ) ,(5) V J ( u n ’ v n )

x = x ( u n , v n ) = u n

” y = x ( u n

Sy_f d u ⁿ ’

\ dy v n ) = v n ' , L d v

[Sy] JN]

Ln\        I I I I ’ у   V du ) V dv )

(ex ( u , v ) d y ( u , v ) ex ( u , v ) dy ( u , v ) ] где J ( u , v ) =I——'---Л - яко-

V d u     d v      dv     du )

биан преобразования, индекс n представляет номера лучей, пришедших в точку (x, y, z) из точек ( u_n , v_n )

плоскости z =0, L_n - расстояние от точки выхода луча до точки прихода луча (x ,y, z) .

Использование формулы (5) на практике приводит к проблеме поиска всех корней системы алгебраических уравнений (6).

В случае, когда корень не единственный, поиск корней становится сложной и неустойчивой задачей. Кроме того, выражения (5), (6) перестают быть справедливыми в области каустик и фокальных точек. Для того, чтобы выражения (5), (6) было удобно ис- пользовать для решения практических задач, необходимо их модифицировать.

Найдем модуль выражения (5)

E ( x , y , z ) E * ( x , y , z ) = L A ⁽ u n ’ v n ’° ) n     J ⁽ u n , v n )

+ a ( x , y , z ) , (7)

a ( x , y , z ) =

Au n * m

v n ^,0 ) A * ( u m , v m ^,0 ) exp ( jk ( y ( u n , v n ^,0 ) ⁺ L„ ( u n , v n W( u m , v m ^,0 ) — ^L m ( u m , v m ) ) )

Наблюдаемая интенсивность света, которая регистрируется прибором (или глазом), имеет вид:

данного метода. Пусть решение скалярного волнового уравнения представляется в виде

U ( x , y , z ) = J G ( x — X i , y — y i )^X x E ( x i , y i , z ) E * ( x i , y i , z ) dx i dy i ,

E ( x , y , z ) = A exp ( ik v ) =

= zL A j ( x , y , z ) exp [ ik V j ( x , y , z ) ] ,

где интегрирование производится по апертуре датчика. Функция G ( x - x i , y - y i ) зависит от устрой-

ства регистрации и, например, может иметь вид га-

уссианы:

G ( x , y ) =

f i exp [" 2

x ² + y²

G 2

2 na ²

где A j , v j — медленно меняющиеся функции. В этом случае функции A , v можно не считать медленно меняющимися. Подставим (12) в уравнение Гельмгольца и получим

L ( ik ( 2 V A j Vv j + A j Av j ) +

где g характеризует размер датчика. При g ^ 0 и к ^ да , выражение (9) можно переписать в виде:

U ( x , y , z ) = L

n

__________________ A 2 ( u n , v n ^,0 ) __________________ e x ( u n , v n ) ^d y ( u n , v n ) e x ( u n , v n ) d y ( u n , v n ) d u       d v         d v       d u

+ ( a A j - к ² A j ( Vv j ) 2 + к ^s A j ) ) x              (i3)

x exp ( ik v j ) = 0.

U ( x , y , z ) =

J 5 ( x - x ( u , v ) ; y - y ( u , v ) ) A ² ( u , v , z ) dudv .

В (10) интегрирование ведется по поверхности, на которой заданы начальные условия.

Практическое использование формулы (10), предполагает замену дельта функции Дирака на ее аппроксимацию, например, на гауссиану

Умножим (i3) на f ( x , y , z ) exp ( - ik v _m ) , где f ( x , y , z ) - произвольная гладкая функция, и проинтегрируем по области пространства, содержащей точку, в которой требуется вычислить поле:

J zL ( ik ( 2 V A , -Vv j - + A j Av j ) +

+ ( a a j - k ² A j ( Vv j ) ² + k ²E A j ) ) X

5 ( x , y ) =

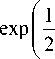
f x ² + y y rG^5-.

2 nG ²

x exp ( ik v j ) exp ( - ik v _m ) x x f ( x , y , z ) dxdydz = 0.

где g - параметр регуляризации (по порядку величины g равно размеру датчика). Формулы (i0), (ii) представляют собой основу целого класса алгоритмов трассировки лучей (ray tracing). Выражение (10) справедливо в окрестности каустик и фокальных точек. В этом случае формула (10) дает значение интенсивности, усредненное по поверхности регистратора. Отметим, что интенсивность, рассчитанная по формуле (5), в окрестности каустик и фокальных точек стремится к бесконечности.

Пренебрегая величинами более высокого порядка малости, будем иметь

J ( ^ik ( ^{2 V} A m ^V v m ⁺ A m ^A v m ) ⁺

+ ( A A m - k ² A m ( Vv m ^ + k 2 S A m ) ) x            (i5)

x f ( x , y , z ) dxdydz = 0.

Учитывая произвольность функции f(x,y,z) в (15), получим уравнения для главных членов асимптотического разложения

2. Модифицированный геометрооптический метод

Рассмотренный выше геометрический или лучевой подход справедлив, если свойства среды и поля изменяются медленно. Рассмотрим модификацию

^div ( 4 2 ^V v m ) = ⁰ , (^V v m ) 2 = ^s .               ⁽ⁱ⁶⁾

Для решения полученной системы дифференциальных уравнений (16) необходимо задать на начальной поверхности значения функций A , v .

3. Асимптотические разложения при использовании дифракционных оптических элементов

Рассмотрим асимптотическое решение уравнения Гельмгольца (1) для случая дифракции на одномерном (цилиндрическом) дифракционном оптическом элементе (ДОЭ).

ДОЭ предполагаем расположенным в области 0 <  z <  a , где 0 и a - минимальная и максимальная высоты дифракционного микрорельефа. Распределение диэлектрической проницаемости в области ДОЭ предлагается описать выражением

е ( x , z ) = Z ^e n ( x , z ) exp [ ikn v ( x ) ] ,           (17)

n где v(x) — эйконал ДОЭ. Под эйконалом ДОЭ будем понимать функцию, определяющую границы зон на оптическом элементе. Границы зон определяются из уравнения

V ( x m ) = m^X .

В области за ДОЭ (z> a ) и в области перед ДОЭ (z<0) диэлектрическую проницаемость считаем постоянной.

Решение уравнения Гельмгольца в области ДОЭ (0 <  z <  a ), в области за ДОЭ и в области перед ДОЭ представим в виде:

E ( x , z ) = ^ Cⁿ ( x , z ) exp [ ikn v ( x ) ] ,        (18)

n

E z > a ( ^x , ^z ) = E T n ( ^x , ^z ) ^ex P ^{[ ikn} v ( ^x ) ] ,       ⁽¹⁹⁾

n

^E z <0 ( ^x , ^z ) =

= ^ ( I n ( x , z ) ⁺ R n ( x , z ) ) exp ( ikn v ( x ) ) ,

n

где функции C n ( x , z ) , Tⁿ ( x , z ) , R n ( x , z ) подлежат дальнейшему определению. Функции I n в (20) определяют подающую волну.

Для решения задачи дифракции достаточно определить функции Tⁿ ( x , z ) , R n ( x , z ) на границах области ДОЭ при z=0 и z= a . Знание поля на границах области рельефа позволяет найти поле в любой области пространства, используя, например, интеграл Кирхгофа.

Производные поля (18) имеют вид:

д ² E ( x , z ) „ д C n ( x , z )    _г ,

—= L — rV^^ex P ^[ ikn v ( ^x ) ] ,    ⁽²¹⁾

дz        n    дz д2 E (x, z) д?

= - ^ exp [ ikn v ( x ) ] Cⁿ ( x , z ) k ² n ² n

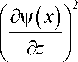
В (22) оставлены только главные члены разложения. Подставляя (17), (21), (22) в уравнение Гельмгольца, получим

Е exp ^[ ikn v ( x ) ] Г ^д C ⁽ ₂ x ’ z ) - n                    l      ^д z

- C ( x , z ) k ' n 2     ' ' ' '| +

^{V 7} l д x J

+ k ² C n ( x , z ) £ e _m ( x , z ) exp [ ikm v ( x ) ] I = 0. m J

Умножим (23) на exp [- ikp v ( x ) ] f ( x ) и проинтегрируем по x по апертуре D . Оставляя только главные члены порядка k ² , получим уравнение:

, р² C p ( x , z ) - _Cp ₍ x k 2 p, V x ) Y +

^J D l     ^д ‘          ' ' l ^д x J (24)

+ E k ²e n - p ( x , z ) C p ( x , z ) J f ( x ) dx = 0.

Учитывая, что уравнение (24) должно выполняться при любой функции f (x), получим для оп ределения функций Cn (x, z) систему обыкновенных дифференциальных уравнений д C (x, z ) _ СР(Х zU2 2 fMx) )

д z 2        C ⁽ x ’ z ) k p I д x I ⁺

+ ^ k 2 ^е n - p ( x , z ) C n ( x , z ) = 0, p = -» , ■/ .

Введем понятие локального периода или локальной ширины зоны ДОЭ х , dv d (x) = X/----, dx

В этом случае уравнения (25) принимают вид:

д ² C^p ( x , z )

^{д z 2}                 l d J                  (27)

+ ^ k ² e n - p ( x , z ) C n ( x , z ) = 0, p = -» , ■/ . n

Уравнения (27) при каждом фиксированном x = x ₀ совпадают с уравнениями для поля внутри дифракционной решетки с периодом d и распределением диэлектрической проницаемости [7, 8]

^е( ^x 0 , ^z ) = Z ^e n ^{( x} 0 , ^{z )ex} p

n

( .2n n ) I i--------x I

Полученный результат позволяет локально описывать ДОЭ дифракционной решеткой.

Решение уравнений (25) представим в виде

C^p ( x , z ) = U p ( x , z ) A n ( x ) + V np ( x , z ) Bⁿ ( x ) , (28)

где An (x)= Cn (x,0), Bn (x) = dC (x,0) . В (28) и dz ниже предполагается суммирование по повторяющимся индексам (правило Эйнштейна). Функции Up (x, z) и Vnp (x, z) в (28) удовлетворяют системе дифференциальных уравнений d 2U,    /    d V    / p lq    p lq dz2 q p , dz2 q p

п

| 8 P + k ² s ” — p , n , p = -« , ■/     (30)

с начальными условиями um (x ,o)=dVmp(x,0)=8 m, dz

dE ( x ,0 )          ₂ру ( x )Y

---------- = ik s-” I----| x dz V (5x J

x ( I ” ( x , - 0 ) - R ” ( x , - 0 ) ) exp ( ik” у ( x ) ) ,

E ( x , a + 0 ) = T ” ( x , a + 0 ) exp ( ik” у ( x ) ) ,

V m ( x ,0 ) = У = 0, dz

8pm - символ Кронекера.

Подставляем (28) в (18) и получаем поле в области ДОЭ:

E ( x , z ) = ( U ” ( x , z ) A ” ( x ) +

+ V ” ( x , z ) B ” ( x ) ) exp ( ikp у ( x ) ) .

Производная поля равна

dE ( x , z ) Г dU ” ( x , z )

dE ( x , a + 0 )            ₂fdy ( x ) )

—------- = ik s - ” I--— | x dz у (5x J xT” (x, a + 0) exp (ik”у (x)).

Запишем условия непрерывности полей изводных (33)-(38) на границах области ДОЭ

T ” ( x , a + 0 ) exp ( ik” у ( x ) ) = ( U ” ( x , a ) A ” ( x ) + + V ” ( x , a ) B ” ( x ) ) exp ( ikp у ( x ) ) .

и

про-

dz ( dl”' ( x, z ) dz

dz

A" ( x ) +

B ” ( x ) | exp ( ikp у ( x ) ) .

На границах области ДОЭ (при z = + 0 z = a - 0) поле и производная имеют вид:

E (x,z) = Ap (x)exp (ikpу (x)), dE (x, z )         , ,      ,       ,

—d---- = B p ( x ) exp ( ikp у ( x ) ) ,

и при

ik

,Гду (x )Y           , s- ”2 —— T (x, a + 0)

I ⁵ x J

x exp ( ik” у ( x ) )

dU ” ( x , a ) dz

A ” ( x )

+-- ” d ’   B ” ( x ) | exp ( ikp у ( x ) ) ,

E ( x , a ) = ( U p ( x , a ) A ” ( x ) +

+ Vp (x,a)B” (x))exp(ikpу (x)), dE (x,z) = Г du”p (x,a) A” (x)+ dz ^ dz

+ — ” d ’ —-B” ( x ) | exp ( ikp у ( x ) ) .

Поле и производная поля перед ДОЭ z = - 0 ) и сразу после ДОЭ (при z = a + 0) быть получены из (19), (20) в виде:

E ( x , - 0 ) = I ” ( x , - 0 ) exp ( ik” у ( x ) ) +

+ R ” ( x , - 0 ) exp ( ik” у ( x ) ) ,

A^p ( x ) exp ( ikp у ( x ) ) =

= ( I ” ( x , - 0 ) + R ” ( x , - 0 ) ) exp ( ik” у ( x ) ) ,

(при могут

B^p ( x ) exp ( ikp у ( x ) ) = ik Is- ”²

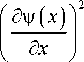
x ( I ” ( x , - 0 ) + R ” ( x , - 0 ) ) exp ( ik” у ( x ) ) .

Умножая уравнения (39)-(42) на exp [- ikp у ( x ) ] f ( x ) и интегрируя по x по апертуре ДОЭ, получим систему уравнений для определения функций A ( x ), B ( x ), R ( x , - 0 ) , T ( x , a + 0)

T^m ( x , a + 0 ) = ( U m ( x , a ) A ” ( x ) + V m ( x , a ) B ” ( x ) )

? Г ду ( x )Y    ,        , Г dU m [x , a) , , dV™ Px , a) , ,)

ik, s- m² ^-(-^ Tm(x , a + 0) = —” ⁽ ’ ) A”(x ) + ” ⁽ ’ ) B ” x)

4       ( 5 x |      ⁽ ’      ) ( dz ⁽ ) dz ⁽ ) |

A p ( x ,0 ) = ( I^p ( x , - 0 ) + R^p ( x , - 0 ) )

B^p ( x ,0 ) = ik

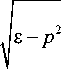
^у ^ ^ ! | ( I^p ( x , - 0 ) + R^p ( x , - 0 ) ) . д x )

Система уравнений (43) при любом фиксированном x совпадает с системой линейных уравнений для определения коэффициентов дифракции на периодической дифракционной решетке с периодом (26) [7, 8].

Поле на выходе ДОЭ имеет вид:

E ( x , a ) = ^ T” ( x , a + 0) exp [ ik” у ( x ) ] .        (44)

n

Для того, чтобы найти поле в области за ДОЭ, будем использовать интеграл Кирхгофа

E ( x• z ) = J E ( x• a )

- ikz

2 ( x - u ) ² + ( z - a ) ²      (45)

x H 11 ( k^ ( x - u ) ² + ( z - a ) ² ) du

Предложенный метод расчета поля (43), (45) целесообразно использовать для расчета полей от ДОЭ с зонной структурой. Зонная структура характерна для ДОЭ, рассчитанных в приближении геометрической оптики. Метод (43), (45) позволяет моделировать ДОЭ с большим размером апертуры в тысячи длин волн. Данный подход является обобщением метода нелинейного предискажения, изложенного в работах [1, 2, 9]. Метод также обобщает приближение Кирхгофа [3, 4].

Пример расчета

В качестве примера рассмотрим ДОЭ, выполненный в виде градана с двумя возможными значениями показателя преломления n ₁ • n ₂ ■ Распределение диэлектрической проницаемости в этом случае описывается следующим выражением:

e( x ) = £o + Ё 2| 6 „I cos (kn v( x) + arg (e „))• n =1

e n =ЛПК (1 - exp (-2л int )) + 2л in

⁺ 2' - ^{exp (} " ² ” int» • e o =П 1 1 + П 2 ( 1 - 1 ) •

где t – коэффициент заполнения диэлектриком с по казателем преломления n 1 ■ Пусть коэффициент t не

меняется от зоны к зоне. В этом случае коэффициенты T ⁿ в (44) зависят от следующих переменных

Tn (x, a + 0) = Tn (n i,n 2, t• a• d (x)) • где d(x) – локальная ширина зоны ДОЭ, a-высота области ДОЭ. Подставляя выражения для коэффициентов T n в (44) и используя интеграл Кирхгофа (45), получим следующее выражение для поля в произвольной точке полупространства z>a

E ^{( x} • z ) = EJ

- ik ( z - a )

2^( x - u ) 2 + ( z - a ) 2

x

x T n

n 1 > n

2 ’ t • a • X

^{- 1} d v ( u ) I du J

exp [ ikn v ( u ) ]x

R /2

I (0 f )= J TJ1

- R / 2

x

n 1 > n 2 > t • a •

( f - a )2

⁽ f )      - du

.

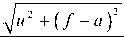
u

x

В параксиальном приближении функция

T ¹( n _1> n ₂> t • a ) = C и не зависит от размера зоны. В

этом случае значение интенсивности в фокусе

I ( 0’ f ) = RC ^X f

совпадает с результатом, полученным по методу нелинейного предыскажения [1, 2, 9].

Заключение

Рассмотрены асимптотические методы решения скалярного волнового уравнения. Разработан новый метод решения задачи дифракции на цилиндрических ДОЭ. Специальные представления для поля и диэлектрической проницаемости в области микрорельефа ДОЭ позволили локально свести задачи дифракции на ДОЭ к задаче дифракции на дифракционной решетке. Данный подход является обобщением методов, основанных на представлении поля в виде системы дифракционных порядков. Предложенный подход можно использовать для получения асимптотических решений системы уравнений Максвелла.

x H ¹ ( k^ ( x - u ) ² + ( z - a ) 2 ) du .

В качестве примера оценим значение интенсивности поля в фокусе одномерной линзы V = - kju ² + ( f - a ) 2 • где (f-a ) - фокусное расстоя-

ние. В этом случае основной вклад в поле в фокусе будет вносить одно слагаемое в (46) при n = 1. Заменим в (46) функцию Ханкеля ее асимптотикой

Г2" Г/ mп л)) Hm (z ) = А “exP I i I z Л Л । । V лz ^X 2   4 J J

и получим

Работа выполнена при поддержке грантов Президента РФ № МД -210.2003.01 и № НШ-1007.2003.1, гранта РФФИ № 01-01-00097 и российско-американской программы «Фундаментальные исследования и высшее образование» («BRHE»).