Асимптотические свойства многочленов ln,n(x) , ортогональных на произвольных сетках
Автор: Магомедова Зарина Магомедовна, Нурмагомедов Алим Алаутдинович
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 2 т.24, 2022 года.
Бесплатный доступ
Пусть Ω={x0,x1,x2,…,xj,…} - дискретная система точек, таких что 0=x0 0 на произвольных сетках, состоящих из бесконечного числа точек полуоси [0,+∞). А именно, установлена асимптотическая формула, в которой при возрастании n вместе с N, асимптотическое поведение этих многочленов близко к асимптотическому поведению ортонормированных многочленов Лагерра L^αn(x).
Многочлен, ортогональная система, сетка, вес, асимптотическая формула
Короткий адрес: https://sciup.org/143178745
IDR: 143178745 | DOI: 10.46698/g5860-8517-3109-i
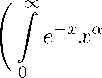
Список литературы Асимптотические свойства многочленов ln,n(x) , ортогональных на произвольных сетках
- Шарапудинов И. И. Смешанные ряды по ортогональным полиномам. Теория и приложения. Махачкала: ДНЦ РАН, 2004. 276 c.
- Шарапудинов И. И. Асимптотика полиномов, ортогональных на сетках из единичной окружности и числовой прямой // Современные проблемы математики, механики, информатики: материалы междунар. науч. конф. Тула: Изд-во ТулГУ, 2009. C. 10–19.
- Шарапудинов И. И. Некоторые свойства полиномов, ортогональных на неравномерных сетках из единичной окружности и отрезка // Современные проблемы теории функций и их приложения: материалы 15-й Сарат. зим. шк., посвящ. 125-летию со дня рождения В. В. Голубева и 100-летию СГУ. Саратов: Науч. кн., 2010. С. 187.
- Шарапудинов И. И. Асимптотические свойства полиномов, ортогональных на конечных сетках единичной окружности // Вестник ДНЦ РАН. 2011. № 42. C. 5–14.
- Шарапудинов И. И. Полиномы, ортогональные на сетках из единичной окружности и числовой оси // Дагестан. электрон. мат. изв. 2013. Т. 1. C. 1–55. DOI: 10.31029/demr.1.1.
- Нурмагомедов А. А. Асимптотические свойства многочленов ˆp, n (x), ортогональных на произвольных сетках в случае целых и // Изв. Сарат. ун-та. Нов. сер. Сер. Математика. Механика. Информатика. 2010. T. 10, № 2. C. 10–19. DOI: 10.18500/1816-9791-2010-10-2-10-19.
- Нурмагомедов A. A. Многочлены, ортогональные на неравномерных сетках // Изв. Сарат. ун-та. Нов. сер. Сер. Математика. Механика. Информатика. 2011. Т. 11, № 3 (2). C. 29–42. DOI: 10.18500/1816-9791-2011-11-3-2-29-42.
- Султанахмедов М. С. Асимптотические свойства и весовые оценки полиномов, ортогональных на неравномерной сетке с весом Якоби // Изв. Сарат. ун-та. Нов. сер. Сер. Математика. Механика. Информатика. 2014. Т. 14, № 1. C. 38–47. DOI: 10.18500/1816-9791-2014-14-1-38-47.
- Dorfler P. Asymptotics of the best constant in a certain Markov-type inequality // J. Approx. Theory. 2002. Vol. 114, № 1. C. 84–97. DOI: 10.1006/jath.2001.3638.
- Магомедова З. М. Об асимптотике многочленов, ортогональных на произвольных сетках // Изв. Сарат. ун-та. Нов. сер. Сер. Математика. Механика. Информатика. 2011. Т. 11, № 3 (1). C. 32–41. DOI: 10.18500/1816-9791-2011-11-3-1-32-41.
- Сег¨е Г. Ортогональные многочлены. М.: Физматгиз, 1962. 500 c.
Статья научная
