Асимптотические свойства решений автономной конечно-разностной системы

В статье рассматриваются свойства решений автономных конечно-разностных систем. Исследование базируется на использовании метода локализации положительного предельного множества с помощью функции Ляпунова.

В работах А. А. Шестакова [3] и Ю. И. Го-лечкова [1] доказано, что метод локализации предельного множества с помощью функций Ляпунова является эффективным методом исследования асимптотических свойств решений кусочно-разностных и функционально-дифференциальных систем динамических процессов.

Рассмотрим автономную конечно-разностную систему

х ( к + 1 ) = f ( х ( к ) ) , f : D ^ R",    (1)

где х ( к ) , f ( х ( к ) ) — элементы и-мерного евклидова пространства R ” , D — открытое множество в R ” .

Определение 1. Точка q е D называется положительной предельной точкой решения ф(к, р) системы (1), если:

• а)    3^ } с [ О,^к+ ) , ф ( А ^ ,р ) ^ q, h ^ ^к+ ;

• б)    положительным предельным множеством И ( ф ( к ) ) решения ф ( к, р' ) системы (1), проходящего через точку р, называется множество всех положительных предельных точек решения.

Определение 2. Функция У : D ^ Rⁿ, D с R ” называется скалярной функцией Ляпунова на множестве, если:

• 1)    У(х) непрерывна по х е У;

• 2)    АУ ( х ) < 0 Ух е У, где АУ(х) — первая разность функции У(х) — определяется соотношением АУ(х) = = У(f(х)) —У(х).

Определение 3. Множеством С-уровня У^-1(с) скалярной функции Ляпунова У(х) для автономной системы (1) называется множество (возможно, пустое)

У ' ( с ) ::= { х е У : У ( х ) = с } .      (2)

Определение 4. Нуль-множеством Z (или нейтральным множеством) скалярной функции Ляпунова У(х) на множестве У для системы (1) называется множество

Z ::= { х е У : ДУ ( х ) = 0 } .

Через Е обозначим наибольшее инвариантное множество, содержащееся в Z. Рассмотрим функцию У⁽¹⁾ = (Ур ..., У _г ), отображающую пространство R ” в R^r. Первую разность АУ⁽¹⁾(х) для функции У⁽¹⁾ = = (Ур ..., У_г) определим соотношением

АУ(1)(х) = У(1)(f(х)) —У(1)(х).

Определение 5. Функция У⁽¹⁾ : R ” ^ R^r называется вектор-функцией Ляпунова первого типа на множестве У для системы (1), если:

• 1)    У⁽¹⁾(х) непрерывна в R ” ;

• 2)    АУ ^{( 1 )} ( х ) < 0 Ух е У.

Через /Я * обозначим наибольшее инвариантное множество, содержащееся в Z⁽¹⁾, где

• Z^ ::= | х е У : Д У^ ( х ) е у | .

Пусть У с R ” , У⁽²⁾ : R ” ^ R^r , У ^ = = max уЯ( х ), У⁽²⁾(х) = Т/Я (f(х)) -

• - У ^ (х) • м, где м = (1, ..., 1) — r-мерный единичный вектор.

уЯ = у/² ) ( / ( х ) ) - уЯ ( х ) , I = 1, 2, ..., г .

Определение 6. Функция У⁽²⁾ : R ” ^ R^r , называется вектор-функцией Ляпунова второго типа на множестве У для системы (1), если:

• 1)    У⁽²⁾(х) непрерывна в R ” ;

• 2)    1 7 Я ( х ) < 0 Ух е У.

Через Е(2) обозначим наибольшее инвариантное множество, содержащееся в Z(2), где

Z ^ ² ::= | х е У : У ) ^{2 )} ( х ) = о | .

Теорема 1. Пусть

• 1)    У ( х ) — скалярная функция Ляпунова на множестве У сО для системы (1);

• 2)    ф(к, р) е У, где ф(к, р) есть решение системы (1).

Тогда решение ф(к, р) системы (1) или не ограничено при к > 0, или

Ф ( к , р ) ^ Е П У ^-1 ( с ) , к ^ к *     (3)

где Е — наибольшее инвариантное множество, содержащееся во множестве Z:

Z ::= { х е У : ДУ ( х ) = О } .

Доказательство. Если ф(к, р) не ограничено, то О(ф(к)) = 0 и утверждение теоремы 1 неверно. Если ф(к, р) ограничено при всех к ^ к⁺, тогда предельное множество П(ф) непусто, компактно, положительно инвариантно и является наименьшим замкнутым множеством, к которому приближаются решения, т. е. ф(к, р) ^ О(ф(к)) [3].

Множество П(ф(к)) инвариантно. Значит, П(ф(к)) с Е. Так как ф(к, р) ^ О(ф(к)), ф(к, р) при к ^ к+. Пусть q е О(ф(к)). Тог да 3Д}, к, ^ к*, ф^к,,р) ^ q.

В силу непрерывности функции У ( х ) имеем У(ф(к)) ^ У(q) = с. А так как q е П(ф(к)) любое, то П(ф(к)) с У Чс). Теорема доказана.

В условиях теоремы 1 неограниченное решение может существовать при условии, что У не ограничено и если

3 { ф ( ^кi ^, р ) } ^, ф ( ^кi ^,р ) ^{е У ,} ф(Д р ) ^^

ДУ ( ф ( к , ,р ) ) ^ О, г ^ те.

Теорема 2. Пусть:

• 1)    У⁽¹⁾ : Rⁿ ^ R^r есть вектор-функция Ляпунова первого типа на множестве У с Rⁿ для системы (1);

• 2)    ф(к, р) ограниченное при к > О решение системы (1);

• 3)    ф(к, р) е У Vk е J * , Vp е D , тогда

3с е R^r ф ( к, р) ^ Е^¹ П ( у ^{( 1 )} ) ¹ ( с ) к ^ к ⁺ .

Доказательство. Пусть У(1) есть вектор-функция Ляпунова первого типа. Тогда каж дая составляющая У^ вектор-функции У(1) является скалярной функцией Ляпунова на множестве У. Если ф(к, р) есть решение, ограниченное при к е J+, содержащееся в У, то по теореме 1

3q е R ф ( к , р ) ^ Ер ’ П ( У_у ^{( 1 )} ) ¹ ( с )

при к ^ к⁺, V г = 1, 2, ..., г, т. е.

• 3 с е R^r ф ( к, р ) ^ Е^ П ( у ^{( 1 )} ) ¹ ( с ) к ^ к ⁺ при к ^ к⁺, где с = (у,..., с_г), У⁽¹⁾ = (У_р ..., ..., УД

Замечание. Если У(1) — вектор-функция Ляпунова первого типа на множестве У для системы (1), то каждая составляющая У(1) вектор-функции У(1) есть скалярная функция Ляпунова на множестве У с соот- с (1) ветствующими Z, и Е, . Тогда ,, у яв 4=1

* -

ляется скалярной функцией Ляпунова системы (1) на множестве У, и множества Е(1), Z(1) соответствуют вектор-функции У(1). Если вместо вектор-функции Ляпунова первого типа взять вектор-функцию Ляпунова второго типа, то справедлива

Теорема 3. Пусть:

• 1)    У ⁽¹⁾( х ) есть вектор-функция Ляпунова второго типа на множестве У с Rⁿ для системы (1);

• 2)    ф(к, р) — ограничено при решении системы (1);

• 3)    ф ( к,р ) е У Vк е J * , Vр е D,

тогда

3с е R ф ( к, р) ^ Е < ^{2 )} П ( у ^{( 2 )} ) ¹ ( с ) к ^ к ⁺ .

Пример 1. Рассмотрим двумерную линейную конечно-разностную систему

Х 1 ( к + 1 ) = аХ 1 ( к ) + Ьх' 2 ( к ) ;

Х 2 ( к + 1 ) = сх 2 ( к ) + dx 2 ( к ) .      ⁽¹⁾

Обозначим Д = а • d - с • Ь, 5 = а + d/ (Д + 1).

Пусть функция У(Х ( , Х 2 ) имеет вид:

У ( Х 1 , Х 2 ) = [6X 2 - ( ^й - 5 ) ^х 1 ]² +

+ [с‘Х1 — [q — 5) Х2 [ + ^1 — 5 )(х1 * Х2 ), тогда

ДУ ( Х 1 ,Х 2 ) = У ( аХ 1 + Ьх 2 ,сХ 1 + dx 2 ) -

- V ( х ^ , ^х 2 ) -- ( 1 - Д ² )^ -5 ² )( ^х2 + x₂ ) . Рассмотрим случай, когда 1 - 5 ² > 0, 1 - Д ² > 0. При выполнении условий (2) функция V(x i , х₂) является определенно-положительной, а ДV(X 1 , х₂) — определенно-отрицательной. Здесь Z = Е = {(0,0)}, следовательно, решение X i = Х 2 = 0 системы (1) асимптотически устойчиво. Можно показать, что условия (2) являются и необходимыми для асимптотической устойчивости решений X i =

Пример 2. Рассмотрим двумерную конечно-разностную систему

X i ( к + 1 ) - ах ₂ ( к ) ( 1 + x ^f ( к ) ) ; х₂ ( к + 1 ) - bx i ( к ) ( 1 + x f ( к ) ) .

Пусть V ( X i ,х₂ ) - х ² ( й ) + х₂ ( й ) . Тогда

ДУ ( x_b Х 2 ) =

^^^^^е

Ь ² ( 1 + х₂ ) ² -

1 х ² +

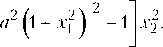
Случай 1. а² < 1, Ь² < 1. Так как ДЕ ( х₁,х₂ ) - ( Ь ² - 1 ) х ² + ( а ² - 1 ) х₂, V есть

функция Ляпунова на R² для системы (3). Здесь Z = Е = {(0,0)}, и, так как каждое решение ограничено, по теореме 1 каждое решение стремится к началу при й ^ й ⁺ . Далее видим, что начало — глобальная точка притяжения. Отсюда следует, что в этом случае начало асимптотически устойчиво в целом.

Случай 2. а ² < 1, Ь ² < 1, а ² + Ь ² < 2.

Случай 3. а² = Ь ² =1. Vопять является функцией Ляпунова, все решения по прежнему ограничены. Здесь Z = Е есть объединение двух координатных осей. По теореме 1 существует такое с, что каждое решение стремится к множеству {(с,0),(0,с),(-с,0),(0,-с)}, являющемуся пересечением Z с окружностью х ² + х₂ - с ² . Имеют место два подслучая:

• (1)    аЬ = 1. Тогда

f (с, 0) = (0, Ьс), f (f (с,0)) - f (0, Ьс) - (аЬс,0) - (с,0).

Так как предельное множество инвариантно связно, решение стремится к одному из этих периодических движений — началу или периодическому движению с периодом 2.

• (2)    аЬ =1. Здесь

f (с,0) = (0,Ьс), f (f (с,0)) - f (0, Ьс) - (-с,0), f (-с, 0) = (0, -Ьс), f (f (с,0)) - f (0, -Ьс) - (-аЬс,0) - (с,0). Если с * 0, то имеем периодическое движение с периодом 4. Как и в первом подслучае, каждое решение стремится к началу или к одному из таких периодических движений с периодом 4.

Случай 4. а ² > 1, Ь ² > 1. Пусть В _в = = В(0,5)::= { ( х₁,х₂ ) : х ² + х₂< б ² | . Для х е В ₅ и достаточно малого 5 имеем:

ДV =

Ь ² ( 1 + 5 ² )

2          :

^х 1 ^{+ а}

'² ( 1 + 5 ² ) ^-1

х ₂ > 0,

Можно считать, что а ² < 1, Ь ² - 1, ив этом случае V есть функция Ляпунова на R ² . ДЕ <  ( а ² - 1 ) х₂ и Z - { ( х₁, х₂ ) : х₂ - 0 } .

Так как Е = {(0,0)}, значит, начало асимптотически устойчиво в целом.

где ДV есть функция Ляпунова на В ₅ при достаточно малых 5 и Е = Z ={(0,0)},. Исключая начало, нет решений, начинающихся в В ₅ и стремящихся к началу изнутри В ₅ (расстояние от начала возрастает), и из Д^^) = (0,0) следует, что х 1 = х 2 = 0. Поэтому по теореме 1 каждое такое решение должно покидать В ₅ (неустойчивость), и так как нет нетривиальных решений, достигающих начало за конечное время, не существует нетривиальных решений, приближающихся к началу при достаточно малых 5.