Асимптотика решений однородного бисингулярно возмущенного дифференциального уравнения в теории обобщенных функций

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 517.928                                        

Исследование асимптотика решений сингулярно возмущенных дифференциальных уравнений в случае смены устойчивости рассмотрено в работах [1, 2, 4-9]. Введено понятие регулярной и сингулярной областей [9, с. 42]. Регулярная область будет ограниченно или неограниченно относительно координатных осей. Если область регулярно, то доказано асимптотические близость решений возмущенной и невозмущенной задачи. Присутствия малого параметра дифференциальных уравнениях при старших производных обусловляется появлением пограничного слоя. Поведения решений сингулярно возмущенной задачи в пограничных слоях достаточно изучено в работе [9, с. 62].

Уникальный метод в этом направление считается метод линии уровня [1, с. 21]. Линии уровня аналитических функций полностью покрывает регулярной и сингулярной области. Но в сингулярной области не выполняется асимптотической близость решений возмущенной и невозмущенной задачи. Актуальность данной работы заключается в том, что впервые доказано асимптотические близость решений возмущенной и невозмущенной задачи в сингулярной областей. Решение задачи рассматривается в пространстве обобщенных функций [3, с. 24].

Постановка задачи. Рассмотрим задачи

£ y ’( t , £ ) + D ( t ) y ( t , £ ) = 0 (1)

У ⁽ t о , ^£ ) = У ⁰.

где 0 <  £ — малый параметр, D ( t ) = diag ( Л ( t ), Л ( t ) ) , y⁰ = colon ( y 0° , y 0 ) - постоянный вектор, t e R . Диогнольная матрица-функция имеет кратную собственные значение Л ( t ) = Л ( t ) = a ( t ), a ( t ) e C " ( R ¹).

U. Пусть выполняются условия: a ( t ) >  0, при t e ( t *, +да ) ; a ( t ) <  0 при t e ( -» , t * ) , a ( t * ) = 0.

Систему (1) можно рассматривать как возмущенную по отношению к вырожденной системе

D ( t )~ ( t ) = 0.

Вырожденная система (3) имеет единственное классическое решение

~( t ) = 0, D ( t ) ^ 0 .

Такие случаи рассматривались в работах [1, 2, 4-9] и доказано асимптотические близость решений задачи (1)-(2) и (3). Асимптотическая оценка верна, в регулярных областях.

Собственные значения матрица-функция D ( t ) в точке t = t * обращаются в нуль. Эти точки называются точками поворота. Поэтому определим обобщенные решения [3, с. 52] задачи (3) в точках t = t * .

Теорема 1. Вырожденная система (3) имеет обобщенные решения вида

~ ( t ) = G ( J ( t - 1 ’ )).

Доказательство. Рассмотрим ряд Тейлора с интегральным остаточным членом:

^{ф (} x ) = ^ф ( t 0 ) ^{+ ф (}t 0 ⁾⁽ t ^- t 0 ) ⁺ ••• ⁺ ~^{Ф n )(} t 0 ^{) ( t} - t 0 ) n ⁺ n!

x ₀) ^{n + 1} d т , ( x e R , n >  0 ) .

+   J фn+1)(Tt + (1 — T)x0 X1 — T)n(x

—

n ‘ 0

Интегрируем (6), исходя из формулы Ньютона-Лейбница и многократо интегрируя по частям правую часть, получаем f (t) = f (t •) + J f 'Ss) ds = f (t •) — J f( S) d (t — s) = f (t •) — (t — s). f'(s )|

t

t

t

+

t

* t

t

⁺ J ^f "^{( s )(} t ^{— s} ) ^ds =

t

...

t

^{( n} )     *                      ‘ r^{( n + 1)}

= f ( t * ) + ... + ( t — t *) ⁿ + f ( s ) ( t — s ) n ds . n !                        *       n!.              ^!

t

Остаточный член преобразуем с помощью замены

t - s = t - Г - Tt + Tt* ^ t = t* + т(t -1 *), (0 < r < 1).

Таким образом,

t — t =(1 — т)(t — t ).

Поэтому остаточный член приобретает вид:

J f

^{( n + 1)}( t * + т ( t — t * )

n !

(1 — т)n (t — t1)n+l dT.

Согласно смыслу задачи, требуется найти правило, по которому нужно вычислять

W e S ( R 1 ), если ( d ( t )~( t ), ф ( t ) ) = 0 при любой

значение (y(t),w)  для любой функции

умноженная на

бесконечно дифференцируемую функцию на

функции ф ( t ) e S ( R ¹).

По определению, обобщенную, имеем

D ( t )~ ( t ), ф ( t ) ) = ( ~ ( t ), D ( t ) ф ( t ) ) = 0.

Таким образом, значения искомого функционала y ( t ) на всех функциях вида D ( t ) ф ( t ) равна нулю. Заметим, что наличие множителя ( t — t * ) n ⁺ 1 у функции ( t — t * ) n + 1 ф ( t ), ( n >  0 ) означает, что это функция при t = t * обращается в нуль. Покажем, что верно и обратное, т.е. если a ( t * ) = 0 для некоторой функции a ( t ) e S ( R 1 ) , то a ( t ) представима в виде a ( t ) = ( t — t * ) n ^{+ 1} в ( t ), где в ( t ) — некоторая функция из S ( R ¹). Действительно, пусть a ( t * ) = 0, a ( t * ) e S ( R ¹). Воспользуемся формулой (6) при t = t *, n = k :

a(t) = a(t*) +... + ^ISH(t — t*)k + (t— t )   fa(k+1)(t* + т(t — t*))(1 — т)kdr = (t — t*)n+1 вt), k! v '           k!

!  1

где в ( t ) =     a^{( k + 1)}( t* + т ( t — t* )) ( 1 — т ) ^k dr . Очевидно, что в ( t ) e S ( R ^!), поскольку a ( t )

k Ц принадлежит в S (R'). Следовательно, a(n)(t) принадлежит в S (R').

Пусть теперь w ( t ) — произвольная функция из S ( R 1 ). Нам нужно найти, чему равно

(y ( t ), w ( t )) . Рассмотрим вспомогательную функцию

_W ^{( k} ) ( t* ) ^{a (} t ) = W ⁽ t ) ^— W ⁽ t*^o ^— W'⁽t* ) ^ 1 ^— ...--- — ^ k .

k !

Отсюда

Г~                                                   1//⁽ k)

0 = (у ( t ), а ( t )) = у ( t ), w ( t ) - w ( t * ) _А - w '( t * V - ... - Г-S-l V k = ( ~ ( t ), w ( t ) ) к                                                ^к •                        )

⁽ k )

- W ( t* ) ( y ( t ), _А ) - ^ ( t* ) ( у ( t ), ^ 2 ) - ... - ^-) (У (t ), V k ) .

Из соотношения (7) получаем, что

У            У           У           У                У

⁽У( t Ш t )) = W ⁽ t ^{) (} У⁽ t ), V 1 ) + ^ '⁽ t ДУ⁽ t ), V 1 ⁾⁺ W "⁽ t ^{) (} У⁽ t ), V 2 ⁾⁺ ... ⁺ W  С t ^{) (} У⁽ t ), V k ) .

Здесь

( у( t ), w ( t ) ) = W ( t * ) c 0 + W ’( t *) C 1 + ... + W^(k ) ( t *) C k , где C k = ( y ( t ), V k ) к = 0,1,2,....

Из определения 5 - функции, получаем, что

(У (t), w( t)) = (co 5( t -1 *) + C 5' (t -1 *) +... + C 5(k) (t -1 *), w( t)), где Ck = (У (t), Vk), k = 0,1,2,....

Таким образом, обобщенные решения задачи (3) имеет вид (5)

Г^У                            ^                          ^                                      ^                          *

y(t ) = C q 5 ( t — t ) + C j 5 ( t — t ) + ... + C^ 5  ( t — t ) = G( 5 (t — t )).

Теорема доказана.

Общие решение задачи (1), (2)

с

t

к

y ⁽ I , е ) = y exp - - J a ⁽ s ) ds .

к

Т0

)

Основная задача, при каких t выполняется предельный переход lim y (t, е) = У(t) .                                                     (9)

e У 0

Определение 1. Последовательность обобщенных функций y_n ( t ) е S '( R ') сходится, если 3 y n ( t ) е S ’( R ' ) такая что V ^ ( t ) е S , ( У п ( t ), ф ( t ) ) у ( у ( t ), ф ( t ) ) .

п УХ

Сходимость такого типа называют слабой сходимостью (или поточечной).

Определение 2. Последовательность функций называется 5 - образной, если она сходится к 5 - функции.

Теорема 2. Если выполняется условие U , тогда для решения задачи (1), (2) справедлива оценка

||y(t,е) - У(*)|| ^ Cen, здесь п = 2k, k е N, 0 < C - некоторые постоянное число.

Доказательство. Учитывая определение 1. в равенстве (8) рассмотрим как последовательность гладких функций

Г    Гу     А   А

⁽ y _£ ⁽ t , ^е ), ^{ф (} t ))

y ⁰ exp-- J а ⁽ s ) ds ^{, Ф (} t )

к        kt 0        )      )

Для вычисления предела исследуем семейство значений ( y_b ( t , е ), ф ( t ) ) при е У 0₊ ,

У ф ( t ) е S ( R ¹). Тогда

+от —J a ( s ) ds                                    +от —J a ( s ) ds

( y _£ ( t, £ ), ф ( t ) ) = y ⁰ J e ' ⁰      [ ф ( t ) - ф (0) ] dt + y ^о ф (0) J e ' ⁰      dt .

-от

-от

b

+от

Отсюда, второе слагаемое равенство (11) верно у ⁰ J y_£ (t , £ ) dt <  y⁰ J e

a ( s ) ds

£ t0      dt = 1

a

-от

Сделав     замену     —j= = z,     мы     видим,     что     при     a < 0 < b nd £

b

b lim f y£ (t, £) dt = lim "Uy  \ exp

£^0 J               £^0        J a                                a      \ nn£

dz = 1. Осталось показать, что в равенстве (11)

первый интеграл справа стремится к нулю вместе с £ . Имеем:

+от                                        a £ ^{- 5}                                         b £ ^{- 6}

J y £ ⁽ t , ^{£ ) [ Ф (} t ) - ^ ^{(0) ] dt} = J y £ ⁽ t , ^{£ ) [ Ф (} t ) - ^ ^{(0) ] dt +} J y £ ⁽ t , ^{£ ) [ Ф (} t ) - ^{Ф (0) ] dt +}

-от                                        -от                                          a £ ^{- 5}

+от

+ J y£ (t, £)ф(t) - ф(0)]dt. Здесь a < 0 < b, 0 < 5 < — .

n

b £ - ⁵

Возьмем норму

+от

J y £ ⁽ t , ^{£ ) [ Ф (} t ) - ^ ^{(0) ] dt}

-от

a £

■ 5

b £ ^-

J y £ ⁽ t , ^{£ ) [ ф (} t ) - ^ф (°) ^{] dt} + J y £ ⁽ t , ^{£ ) [ ф (} t ) - ^ ⁽⁰) ] dt

-от                                          a £-⁵

+

+от

+ J y£ (t, £)[ф(t) - ф(0)]dt < constO(exp b£ - 5

t

\

^“

\           t 0

[ a £ ⁵ , b £ ⁵ ]

где через const обозначены оценки [ф("[dt) - ф(0)] на полу бесконечных интервалах. В силу непрерывности ф(t) и с учетом 5 < — последнее слагаемое в этой оценке стремится к n нулю при £ ^ 0. Таким образом оценка (10) верна. Теорема доказана.

Рассмотрим пример. Пусть a ( t ) = t . Задача (1),  (2) имеет решение вида

1    -—

y ( t , £ ) =       e ^{2 £} . Начальная точка выбрано в неустойчивом интервале и равно t₀ = 0.

у 2 п£

Если возьмем формально £ = 0, то получим t~ (t) = 0.                                                        (12)

Учитывая теорему 1, обобщенные решения вырожденного уравнения (12): ~ (t) = С05( t), где Со - некоторая постоянная, 5(t) - функция Дирака порядка сингулярности равна 1.

Осталось показать, при каких значениях t выполняется равентсва (9). Пусть

( y_£ ( t , £ ), ф ( t )) ^ ф (0) или y_£ ( t , £ ) ^ 5 ( t ). Для этого £ ^ 0                    £ ^ 0

+от                          +от                                              +от

⁽ y £ ⁽ t , ^£ ), ^{Ф (} t )) = J y £ ⁽ t , ^{£ ) Ф (} t ) ^dt = J y £ ⁽ t , ^{£ ) [ Ф (} t ) - ^{Ф (0})]^ ^{+ Ф (0)} J y £ ⁽ t , ^£ "dt

-от                          -от                                              -от

+от                                  +от t ²

Вторая слагаемая в правой части равенства (13) равна ф (0) j y _E ( t , е ) dt = —/ = J e ^{2 Е} dt .

-от

-от

Становится видным после замены переменной -7= = z , этот интеграл равен единице.

е

Осталось показать, что первый интеграл в равенстве (13)

стремится к нулю вместе с е .

Заметим, что V a >  0 и 0 <  3 < — . Тогда имеем

+от j Уе (t, Е)dt =

--Е аЕ 2

2 у П

от         t ²

j e ² dt =

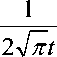
t^

x e ²

—

.-t

аЕ'

- 3

от

j

а Е

. - 3

t2                 __a

' x e ⁷ dt = O ( e ^{2 E 2 3} ).

2d n t          ^{E > 0}

Поэтому

+от 1

-от 2X^exp

^~

k

t— [ ^ф ( ^t ) ^- ^ ^{(0) ] dt 2}

a E

J

-от

2 4n

exp

—

<

у ^{[ ф (} ^t ) - ^ ^{(0) d}t + j

²  /                                        _ _-

-r= x

r x exp ■ k

у x 2 7

[ф ( JEt ) - ^ (0) ] dt +

+от

J

- 3

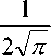
exp

k

t2 k

2 7

- a E

. - 3

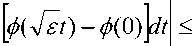
< const x O (exp

(   „ 2 \

a

k 2s 7

+

г ^mF. ^{ф (} ^t ) - ^{ф (0)}1

[ - a E ³ , a E ³ ]

где через const обозначены оценки Ф(y/st) - ф(0) на полубесконечных интервалах. В силу непрерывности ф(t) и с учетем 3 < ^ последнее слагаемое в этой оценке стремится к нуля при Е ^ 0. Отсюда видно, что предельный переход (9) выполняется.

Результаты и обсуждение

Из выше доказанных теорем видно, что в пространстве обобщенных функций S ’( R 1 ), можно установить асимптотическую близость решений бисингулярно возмущенных и невозмущенных задач в сингулярной области.

Работа обсуждено на основе примера на научном семинаре кафедры математического анализа под руководством профессора С. Каримова.

Выводы

Известно, что [1, 2, 4–9] точки смены устойчивости относится к сингулярных интервалах. Если начальная точка выбрана в сингулярном интервале, то поведение решений задачи (1), (2) неизвестно. Поэтому начальная задача выбрана, как бесконечно большая величина. В классической теории функции получать асимптотические оценки задачи (1), (2) в особой точке практически невозможно. Это видно в равенство (4). В работе [9, с. 52] сделано попытка получить оценку в окрестности особой точки. Работа велась в комплексной плоскости. Если переходим к теории обобщенных функций, то показать асимптотические близость решений (1), (2) и (3) возможно в пространстве S'(R1).