Асимптотика решений сингулярно возмущенной задачи
Автор: Акматов Абдилазиз Алиевич
Журнал: Бюллетень науки и практики @bulletennauki
Рубрика: Физико-математические науки
Статья в выпуске: 1 т.10, 2024 года.
Бесплатный доступ
В работе исследована асимптотика решений сингулярно возмущенных дифференциальных уравнений. Нули собственных значений матрицы лежат в действительной оси. Переходя к комплексной плоскости определим отрицательную область, в которой проводится исследование. Линии уровня полностью покрывают эту область. Одна из линий уровня разделяет область на четыре части. В каждой из этих частей области выбираем пути интегрирования. Пути интегрирования должны быть убывающими от начальной до последней точки. Проводя вычисления по выбранному пути интегрирования получим асимптотические оценки решений сингулярно возмущенных дифференциальных уравнений.
Сингулярное возмущение, начальная точка, линии уровня, затягивания потери устойчивости, путь интегрирования, асимптотика, малый параметр
Короткий адрес: https://sciup.org/14129034
IDR: 14129034 | УДК: 517.928 | DOI: 10.33619/2414-2948/98/01
Текст научной статьи Асимптотика решений сингулярно возмущенной задачи
Бюллетень науки и практики / Bulletin of Science and Practice
УДК 517.928
В работе рассматривается случай, когда нули собственных значений матрицы D(t) лежат в действительной оси. Случай, когда нули собственных значений лежат в комплексной плоскости рассматривались в работах [1–2, 4–6] и доказано что выполняется явление затягивания потери устойчивости решений сингулярно возмущенных дифференциальных уравнений [5]. Цель исследования: доказать асимптотическую близость решений сингулярно возмущенных дифференциальных уравнений и соответствующих невозмущенных уравнений, в случае смены устойчивости на основе конкретного примера.
Материалы и методы исследования
Рассмотрим задачу
£ X ' ( t, £ ) = D ( t ) x(t , £ ) + £[h ( t ) + f ( t , x ( t , £ )) ] (1)
X(t0 , £) = X° (£) , ||x0 (£)|| = const где 0 < £ — малый параметр, t e [t0, T] , f (t, X(t, £)) = colon (f (t, X(t, £)), f (t, X(t, £))) ,
h ( t ) = = colon (h 1 (t ), h 2( t)) , D(t ) =
( 4 1 )
, 0 t . )
где 2 ( t ) = t - 1 , X (t , £ ) = colon ( X 1 ( t , £ ), X 2( t , £ ) ) -
искомая неизвестная функция.
Для решения правой части поставленной задачи (1) требуется выполнение следующих условий:
U1. f ( t , x ) e Q ( H ) - пространство аналитических функций в области Н , f ( t ,0) = 0 ,
I f ( t,x ) - f ( t,x ) < M x ~ - ~ , 0 < M - некоторая постоянная.
U2. 2 ( t ) = t - 1 < 0 , 0 < t < 1; 2 (1) = 0 ; 2 ( t ) = t - 1 > 0 , 1 < t < 2.
Имеет место следующая теорема:
Теорема. Пусть выполнены условия U1-U2. Тогда V t e [ 0,2 ] решение задачи (1)-(2)
существует, единственно и для него справедлива оценка
||X ( t , £ )|| < C £ (3)
где C - const .
Доказательство. Задачу (1)-(2) заменим интегральным уравнением
z
t
t
z
t
X ( t , £ ) = X 0
( £ )exp 1 DD ( s ) ds + jexp 1 J* D ( s ) ds [ h ( t ) + f ( t , x ( t , £ )) ] d I £ 0 J 0 I £ T J
t
V
V
Для доказательства существования решения уравнения (4) применим метод последовательных приближений.
Последовательные приближения определим следующим образом:
X 0 ( t , £ ) = 0 ,
z
t
\
t
z
t
A
X n ( t , £ ) = X °
t tt
( £ ) exp I £ J D ( s ) ds I+ j exp I £ J D ( s ) ds I • [ h ( t ) + f ( t
V
J
V
t
J
, X n - 1 ( т , £ ) ) ] d T
где xn ( t , £ ) = colon ( x 1 n ( t , £ ), x 2 n ( t , £ ) ) , n e N .
Далее будем считать, что t = tY + it2; t = t + T2 , где tj, t2, t , t2 — действительные переменные. Тогда получим t2 11
j 2(s)ds = j 2(s)ds = —- t = “[(t - 1) - 1] = [(t 1 - 1) - t2 - 1] + it2 (t 1 - 1) , t0 0 2 22
u ( t 1 , t 2 ) = Re j 2 ( s ) ds =T [ ( t 1 - 1 ) 2 - t 2 - 1 ] =“ [ t 12 - 2 t 1 - t 22 ] ,
0 22
& (t, , t 2) = Im J Д 5 ) ds = t2 ( tx - 1) .
Справедливы оценки:
II A ( 1 1 , t ,)||
x 0( s )exp
Is
1 1 + it 2 Л
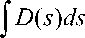
о 7
= O ( s ) ,
при u ( t j, t 2) < 0 , где
D ( t ) =
< t - 1
I 0
A
t -1)
x 0(s) = colon (x10(s), x 0(s)) , ||A(tx, t2 )|| = colon ( Aj (tx, t2 )|,| A2 (tx, t2 )|) . Поэтому будем
рассматривать замкнутую область Ho = {( t j; t 2): u ( tx , t2 ) < 0 } (Рисунок 1).
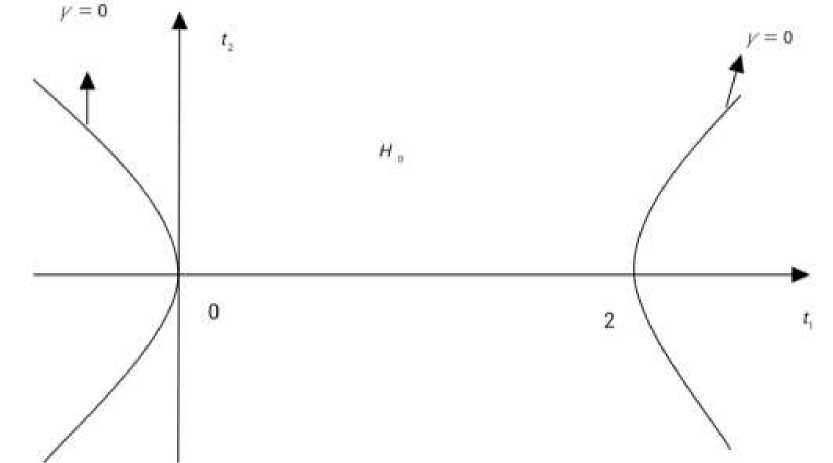
Рисунок 1. Область H 0 .
Если ( t j, t 2 ) e Ho
то
0 x 1
1 t 1 + it 2
( s )exp - R s — 1) ds S I
t} + it-
! 2
= O ( s ).
\
Для того, чтобы последовательные приближения были ограниченными величинами, необходимо выполнение, условия u ( tx , t 2) — u ( т , T ) < 0 то есть путь интегрирования должен быть таким как убывающим от начальной точки до последней точки. Таким образом, путь интегрирования будем выбирать так, чтобы имело место неравенство
u ( t j, t 2) < u ( т , T )
от начальной точки до конечной точки (tj, t2). Это есть главное требование на выбор пути интегрирования для последовательных приближений. Для всех последовательных приближений путь интегрирования будет неизменным.
Пусть u(^, t2) = / ((t2 — 2^ — 12 )= 2/) где y — действительное число. Если y > 0 , то гиперболы будут расположены правее от особой критической линии u(tx, t2) = 0 . Если
— 1 < / < 0 , то гиперболы будут расположены левее от особой критической линии u ( tx , t2 ) = 0. Если / = — 1 то гиперболы вырождаются на прямые t2 = ± ( t j — 1 ) . Если / < — 1 , то гиперболы будет расположен верх (вниз) между двух прямых t2 = ± ( t x — 1 ) (Рисунок 2).
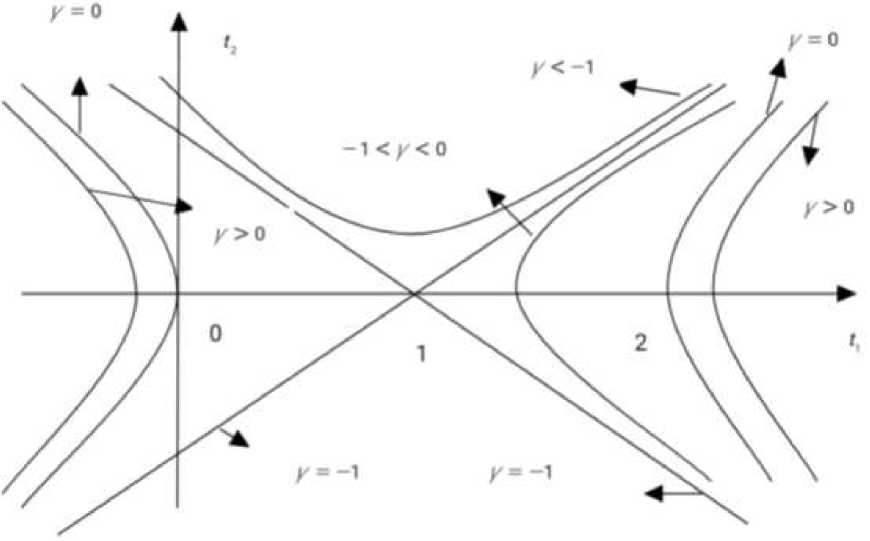
Рисунок 2. Расположения линий уровня в области H .
Для любой гиперболы u (ty, t2) = у прямой t2 = ty -1 или t2 =-ty +1 является асимптотой.
Для нас особый интерес представляют поведения решение на отрезке 1 < ty < 2.
Пусть область H множество точек (ty, t2) ограничившим с левой стороны полу прямыми t2 = ±(tj — 1 + Js) (1 — V^ < tj < +®j с правой стороны ограничена полу прямыми t2 = ±(tj — 2) ( 2 < т <+да ). H = Hv оН2 , где Hy = {t,t2):(ty,t2)e Hи t2 > 0} ,
H 2 ={(t 1, t 2):(t 1, t 2)eHи t2 > 0}. Справедливо: Hy nH2 =[1,2] ; H1 , H2 — симметрично относительно действительной оси Ot и обе бесконечные области.
Решение задачи будем оценивать в замкнутой области H . Если пути интегрирования симметричны то сразу получим, оценку решения задачи в H . Таким образом, будем оценивать решение задачи в области H . Сначала определим убывающий путь интегрирование для замкнутой области H .
Пусть ( ty , t 2 ) e Hy . Тогда t 1 — 1 > 0 , t 2 > 0 ; ( t 1 — 1 ) + t 2 > ty — 1 . Между двумя линиями уровня u ( ty , t 2) = 0; u ( ty , t 2) = —у при t2 = 0 имеет место неравенство 1 > ty — 1 > 1 — 2 y . Линия уровня u ( ty , t2 ) = 0 равносильно равенству (ty — 1 ) 2 — 1 2 = 1 или 1 2 — 2ty — 1 2 = 0, а также линии уровня u ( ty , t2 ) = —y равносильны равенствам ( t j — 1 ) 2 — t f = 1 — 2 y или 1 2 — 2ty — 1 2 =— 2 y . Между двумя линиями уровни лежат части искомой линии K .
Через Г обозначим множество точек гиперболы u ( ty , t 2) = 0 на плоскости, а через Гу обозначим правую половину гиперболы u ( ty , t 2) = 0 : Гу = Г n Hx . Две линии гиперболы u ( ty , t2 ) = 0 и прямой ty + 12 = 2 пересекаются в единственной точке ( 2,0 ) :
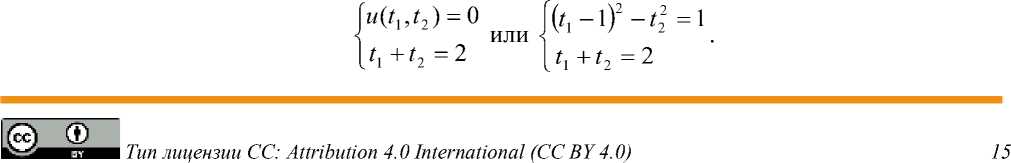
Запишем в виде
(t1 - 1) — 12 =
^ tx + 12 = 2
(t1 - 1)+ t2
или <
( t 1 — 1 )- t 2 = 1
t l + t 2 = 2
Отсюда получим единственную точку пересечения двух линий (2,0). По вертикальной прямой точки гиперболы и(^, t2) = 0 лежат выше (не ниже) чем соответствующие точки прямой tj +12 = 2 . Поэтому для точек гиперболы имеет место неравенство (tt —1) +12 > 1. Таким образом, для точек гиперболы Г справедливо неравенство: из (^ — 1)2 — 12 = 1
получим ( t j — 1 ) — 12
( t , — 1 ) + 1 2
< = 1 или
t — 1) —12 < 1. Отсюда tj — 2 < t2.
По вертикальной прямой точки гиперболы Г лежат выше ( не ниже), чем соответствующие точки прямой t j — 12 = 2 ( ( t j — 1 ) — 12 = 1); по горизонтальной прямой точки гиперболы Г лежат левее чем соответствующие точки прямой.
Таким образом рассмотрим прямую t2 = tx — 2 , по которой спускается + да (плюс бесконечность) до точки (т, т ), т2 = t2, т = t2 + 2 , (tj, t2) — конечная точка на области H. По прямой т2 = т — 2 от начальной точки (2,0) до ( т = +да , т2 = т — 2 = +да ) путь возрастающий. Нам нужен обратный путь. Следовательно, нужный нам путь будет убывающим. Далее от точки (т ,т ) = (ti + 2, t2) по горизонтальной прямой до точки (tj, t2). Это есть последний отрезок пути. l3 = {(т ,т ) :т2 = t2; t2 + 2 > т > tr}. Таким образом, путь интегрирования для l = l0 о 4 о l2 о l3, где
всех последовательных приближений будет неизменным:
l 0 = I 0-1 — 4 ] J ,
4 = {(т, О) т = т — 1 + 4s, 1 — 4s < т < +да /2 = {(т,т):т = т — 2, + да > т > t2 + 2}, h = {(т,т) т2 = t2,t2 + 2 > т > tj}.
Во всех выше указанных пути интегрировании условия (6) выполняется.
Из (5) оценим последовательных приближений на замкнутой области H .
t
t
t
Х [ j( t , s ) = x 0 ( s )exp -j z ( s ) ds + h^ ( r )exp — j 2 ( s ) ds d ^ .
I s J 0 I s^ J
Здесь Re
j T ( s ) ds = 1 [ ( t 1
0 2
— 1 ) 2 — 1 2 — 1 ] = и ( t i, t 2 ) < 0 при t , t 2) e Ho = H о H2 .
t
Поэтому A j ( t , s )| =
x 0 ( s )exp 1 j T ( s ) ds = O ( s ) при t , t 2) e H .
I s 0 J
Остается оценивать
J
t It величины Ц (t, s) = j h\ (т)exp — j T(s)ds dr . Предположим, что |hj(т)| = O(!) при (tl, t2 )e H "0 l гт J
t
t
Тогда |lj (t, s)| = O(1) j exp | — (и(ti, t2) — и(т, т ))||d^ , где l = k о 4 о l2 о l 1 v s J
3 .
1). Будем оценивать величины
Пусть
f exp | —( u ( tx , t 2) — u ( t , t ))r I d T •
V s J l0
t e [o,1 — 4s ]
.
Тогда
u ( t i , t 2 ) — u ( t i , t 2 ) = 1 [ ( t 1 — 1 ) 2 — ( t i — 1 ) 2 ] = 1 [( t 1
—
T1)(t 1 + T1 — 2)] < 2 [(2t 1 — 2)(t 1 — T)] <
< — 4s (1 — T1
T - t j ) • Таким образом
t 1
l 0
----( т 1
V s
—
t j ) d T = 4 s exp
J
Г ^ I
V Vs J
t 1
s 1 — exp
—
t 1
L V vs jj
Получена окончательная оценка f exp | — (u(tj, t2) — u(t ,T ))| • IdT = O() •
V s J l0
2). Рассмотрим интеграл
f exp | —( u ( t j, t 2) — u ( t , t ))r I d T •
Vs J l1
Здесь 4 = { ( т , т ) :1 u ( t i , t 2 ) = 1 [( t i — 1 )
— 2— f exp | — (u (tl, t2) — u (t V s l1 f exp | — (u (tj, t2) — u (t Vs l1 +M • j exp — 1—V s V b • lim exp s ^0 2s ■ 2 — T1 — 1 + 4s }• T22 — 1] = 2 [2(Т1 — 1)^ + s — 1] • ' i,T 2 ' i,T 2 J u (t i, t 2) ^ s J u(t1,t2) sJ X X Г u (tj, t2) • dT = "v2 exp I —1—— Vs — 2s(t — 1) — s +1 I d T • 2s J 1 • Пусть b — const, 1 — 4s< b< +ot • Тогда 41 bb exp Г u (t 1, t 2)— u (W 2) 2dT = ^exp Г <Л)2 • s sJ b —2 4s (t1 — 1)—s+1 V 2s J • exp —24s (^—1)—s+1 b V 2s J • d^ = — 42s exp | u(t 1, t2) = s exp Г ^(^ Vs • • s exp f uMy-u^-^' V £ J _ exp f u(1,.12) - u (b,b -1 + ^) A V £ J = £0р (1)—о (1)] = о (Л). exp £ +1A 2£ J — exp < — 2^£ (b—1) — £+1 V 2£ J Здесь оценка от величины b не зависит. Таким образом, получим оценку r exp I u(11,12) u(W 2) \ d^ = о (). I V £ J e I u(t{, t2 ) — u (T ,T ) A I Теперь вычислим интеграл I exp 1 2---——— I-\dr\ где 12 V £ J 12= {(t 1,12): + ®>т > 2,т2= т — 2}, u(t1,t2) = 2 [(t1—1)2 — T22 —1]= 2 [(t1—1)2 —(t1— 2)2 —1] = T1 — 2 . t2+2 u (1., t,) — u (t ,T) Пусть ^ > b > 0, b — const. Рассмотрим интеграл | exp I v 1, 27-----1 1, 27 I. |dr|. Здесь b V £ J T = T — 2, d^ = dT, dT = 2d-dT, u(Т ,T) = T — 2 • Поэтому j exp ^ u(t 1,12) - u (W2)J. т = ^exp ^u^J j exp f^^Jd^ = = —2^2£ exp u (t 1, 1 2) £ I 2 — T • expI - V 2£ 12 +2 b I u (ti, t2) v 8£ exp I —1—— V £ exp 2—b A 2£ J — I u (tj, t2) — u (b, b — 2) exp I —-—=----------- V £ — _I u(11,12) — u(12 + 2,12) exp I £ = T8£[O (1) — O (1)] = O (£). Таким образом, получена оценка f exp f u(1 p12)— u(T,,T2) I. d I = о(£). 1! V £ J Остается вычислить интеграл Г exp [ u(11,12)— u (т1,т 2)A. d 1. 13 V £ J Здесь l3 ={(t1,T2 :T2 = 12,12 + 2 > T1 > 11 )}, u(11,12) —u(T1,T2) = 2 [(t 1 — 1)2 — (Т1 — 1)2 ]“ —(t 1 — 1)(t1— 11 ) • Получен следующий интеграл j exp I — (u(t[, t2) — u (t ,T )| • dT - j exp I ■ 13 V £ J 13 V — (t 1 — jX^— 11) £ J • dvt Рассмотрим два случая: 1) . Пусть Vs< tx -1. Здесь 0 < b — const: j expfu(t 1, t2) u (w2) у ^< j exp 13 V S J 12+2 (t i— ^ s —У \di\ = O(s), при t{ e (S;l\ O(4s), при tx e [1 + ’ 2) . Случай 1 — Vs< t[ < 1 + Vs . Тогда будем иметь jexpf u(t 1,t2) u(T ,T2) jdT = O(1) J exp[—T1 1)2 1. V s J 12^2 V s J I dT1l t 2 +2 f = O (1) j exp t1 V s (t1 J Пусть T — 1 = s. Тогда 22s T = 1 + V2ss , d^ = Sdds, т = ti, Si t 1 — 1 42s , т — t2 + 2, S2 — t~2 + 1 42s ’ s 1 +w 42s j exp (— s2 )ds < 242s j exp (— s2 )ds — 4444 . s 2 Рассмотрим l3— {(т, t ): т —12, t2 + 2 > т > tx}. Пусть T — {(tj, t2) :1 — Vs< tj < 1,t2 —1\ — 1 + Vs}, T — {(t 1,12) :1 — Vs < 11 < 1,12 — 11 — 1 + Vs }, H10 — H 1\ T. Заметим, что если (tj, t2 )e H0, то величина u(tx, t2) убывает по пути l3. Если (tj, t2 )e T , то величина u (tx, t2) убывает по пути l3при 1 < tx< t2 + 2 , возрастает по пути l3при 1 > tx > 1 — Vs . Это на оценки решения существенно не влияет. Пусть (tj, t2) e T . Тогда будем иметь по пути l : t1 j exp 12 +2 U (t 1, t 2) — U (T1,T 2) s t 1 • |d^ — j exp —J exp 12 +2 , 2 A V 2s J 12+2 dp + j exp V V — 2s 2s J • d^ — dT . J 1 < s , при 1 > т > tj > 1 — Vs , |t — 1 < Vs . Поэтому t 1 j exp V 2s drx — O (4s), j exp 12 +2 V 2s J x 2 A dT1 — O (4s). J +ю Учтено, что интеграл Пуассона j exp (- s2 )ds = . В итоге получена оценка 0 ' 2 । exp ( u (11>1 2) u (W 2) 1. |dr| = о(;.). lз V £ ) Для первого приближения x1 [(t, £) справедлива оценка |xj /1, £)| = O ( 4ё) при (11,12 )eH1 . Таким образом, имеет место оценка, если (1У, 12) е H, то |xn( 1, £)| < C£ где 0 < c — cons1. Аналогично оценка (8) верна для |X21( 1, £)| . Рассмотрим прямую т2= т - 2. Далее рассмотрим особую критическую линию. u (1j, 12) = 0 или (1^ -1)2-12 = 1. Особая критическая линия и прямая 12= 1Y- 2 имеет единственную общую точку (2,0) (точка пересечения двух линий есть (2,0) ). Для точек особой критической линии принадлежащих на H справедливо неравенство (1Г -1) +12 > 1. Поэтому для точек особой критической линии u(1Х, 12) = 0 имеет место (1, -1)-12= у---у----< - = 1. Или (^ -1)-12< 1 (1 j -1)+12 1 , 1j - 2 < 12. Таким образом, по горизонтали точки особой критической линии и(1{, 12) = 0 лежит левее от соответствующей точки прямой 12= 1Х - 2. По вертикали точки гиперболы и(1j, 12) = 0 лежит не ниже (выше), чем соответствующие точки прямой 12= 1Х - 2. Таким образом, оценка (8) имеет место для всех точек замкнутой области H . Аналогично для области H имеет место оценка (8). Теперь рассмотрим сходимости последовательных приближений . Если (^, 12 )е H, то справедлива оценка ||x (1, £)|| < C£, 0 < c - cons1. В дальнейшем, положительные постоянные величины, которые в рассуждениях существенной роли не играют, и поэтому обозначим одной той же буквой C . Тогда IIX2 (1, £) - X 1 (1, £)|| < M JIX т, £)|| exp (u^ib^uhil2!1. dT< < MC £ J exp [ u (1',12) - u (T1,T) \ |dT <(C £ )2 . i v £ ) Получим JX2( 1, £) - X1( 1, £)|| <(C£)2 Далее, имеет место оценка IIXn (t, s) - Xn-1 (t, £)|| < (c Vs )n, (n = 1,2,...) Из (8)-(10) при условии CJs< 1 следует, что последовательность функций xn (t, s) в области H равномерно сходится к некоторой функции x(t, s) е Q(H) , которая является решением (4). Единственность решения обеспечивается условием U1. Теорема доказано. Результаты и обсуждения Линии уровня u(t[, t2) =-1 делят область Но на четыре части. Три из них соответствуют устойчивому интервалу собственных значений. Используя условия устойчивости, получить оценку решений задач (1)-(2) на этих трех областях, не является сложным. Особый интерес вызывает неустойчивый отрезок [1,2]. Поэтому решения задач (1)(2) оценим в области Н, которой обхватывает отрезок [1,2]. Выбираем пути интегрирования, учитывая условие (6), в итоге получим оценку решения задач (1)-(2). Выводы Случай, когда нули собственных значений лежат в действительной оси раньше не рассматривался. Потому что, не выполняется явление затягивание потери устойчивости [3]. Оказалось, что существует убывающие пути интегрирования, и переход к неустойчивому интервалу осуществляется бесконечно удаленной точке. Здесь используем понятие проективной геометрии о параллельных прямых.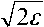
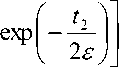
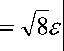
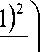
Список литературы Асимптотика решений сингулярно возмущенной задачи
- Алыбаев К. С. Метод линии уровня исследования сингулярно-возмущенных уравнений при нарушении условия устойчивости: дисс. … д-ра физ.-мат. наук. Джалал-Абад, 2001. 376 с.
- Акматов А. А. Асимптотика решений системы сингулярно возмущенных дифференциальных уравнений // Бюллетень науки и практики. 2022. Т. 8. №5. С. 24-31. https://doi.org/10.33619/2414-2948/78/02 EDN NHQTUO.
- Акматов А. А. Кичине козголуунун сингулярдык козголгон теңдеменин чечиминин туруктуулугунун узартылышына тийгизген таасири // ОшМУ жарчысы. 2023. С. 163-168.
- Каримов С., Акматов А. А., Ысакова М. Поведения решений сингулярно возмущенных дифференциальных уравнений в случае смены устойчивости // Естественные и технические науки. 2006. №2. С. 14.
- Тампагаров К. Б. Погранслойные линии в теории сингулярно возмущенных обыкновенных дифференциальных уравнений с аналитическими функциями: дисс. … д-ра физ.-мат. наук. Джалал-Абад, 2017. С. 180-280.
- Турсунов Д. А. Асимптотика решения бисингулярно возмущенных обыкновенных и эллиптических дифференциальных уравнений: дисс. … д-ра физ.-мат. наук. Ош, 2014. С. 52-132. References:.


